Быстрые операции с полиномами

Рис. 14. 10 Быстрые операции с полиномами

вида an 1 xn 1, легко аналитически вычислять производные полиномов и интегралы с подынтегральной функцией в виде многочленов.

Коэффициенты полинома удобно задать как элементы вектора а. Тогда их запись (как элементов вектора) совпадает с общепринятой. При этом помимо своих коэффициентов полином характеризуется порядком п. В документе на рис. 14. 10 представлены задание полинома Р (х) и примеры выполнения ряда операций с полиномом: вычисление значений полинома по заданному аргументу x, вычисление производной полинома Р'(х) и определенного интеграла с полиномом Р (х) в виде подынтегральной функции.

Для вычисления производной и интеграла используются аналитические выражения, что заметно уменьшает время вычислений и позволяет проводить их с предельно малой погрешностью. Все отмеченные вычисления оформлены в виде функций пользователя, что позволяет использовать эти функции в приложениях, связанных с применением полиномов.

Быстрые операции с полиномами-векторами

В математических расчетах широко применяются степенные многочлены — полиномы вида

Р (х) = аn xn+ an 1 хn 1+ + а1 х1 + а0

Ценность полиномов заключается в том, что они могут достаточно точно аппроксимировать многие функции (особенно непрерывные) единообразным способом При этом, поскольку полиномы содержат суммы простых членов

Цифровая фильтрация с помощью БПФ

Аналоговые фильтры обычно имеют довольно сложную аппаратную реализацию. В них применяются громоздкие и нетехнологичные колебательные контуры или RC-цепи с интегральными операционными усилителями. Поэтому интенсивно развивается новый класс фильтрующих устройств — цифровые фильтры. В них используются цифровые логические схемы, имеющие высокую степень интеграции, и применяются цифровые методы обработки сигналов.

Документ на рис. 14. 29 поясняет реализацию алгоритмов цифровой фильтрации с помощью реализуемой цифровыми устройствами функции s (kj). После ее определения синтезируется цифровой сигнал, содержащий низкочастотную в виде перепада и высокочастотную в виде меандра компоненты.

Далее показана реализация фильтрующей операции — свертки для двух типов фильтров, широкополосного и узкополосного. Конец документа, представленного на рис. 14. 29, показан на рис. 14. 30.

Данные о падении парашютиста (конец документа, представленного на рис. 14. 38)

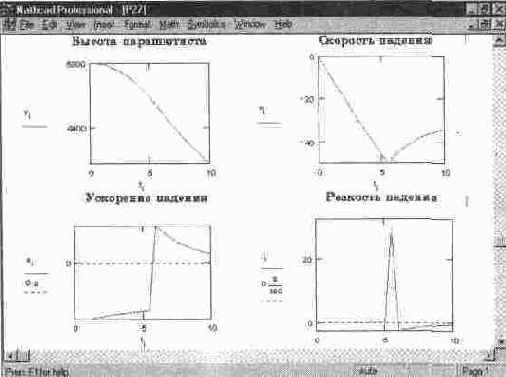
Рис. 14. 39 Данные о падении парашютиста (конец документа, представленного на рис. 14. 38)

В результате моделирования получены зависимости от времени падения парашютиста следующих параметров (см. рис 14 39): высоты, скорости и ускорения падения и резкости (второй производной от скорости) падения. Резкость падения характеризуют перегрузки, которые испытывает парашютист в полете Они многократно возрастают сразу после раскрытия парашюта

Если вас интересуют числовые данные величин, характеризующих падение парашютиста, выведите их в табличной форме.

Электро- и радиотехнические расчеты

14. 8. Электро- и радиотехнические расчеты

Электро- и радиотехнические расчеты — весьма благодатная почва для приложения MathCAD. Некоторые из таких расчетов (например, вычисление емкости или индуктивности различных компонентов) достаточно просты и сводятся (за редкими исключениями) к вычислениям по готовым формулам

В электро- и радиотехнике широко применяются комплексные числа и величины MathCAD обладает всеми возможностями для работы с ними, начиная от вычислений импеданса (полного сопротивления) простых цепей и кончая работой с матрицами, имеющими комплексные элементы

Ниже рассмотрено лишь несколько примеров расчетов электро- и радиотехнических цепей

Фильтрация аналогового сигнала с применением БПФ (конец документа)

Рис. 14. 28 Фильтрация аналогового сигнала с применением БПФ (конец документа)

ставленный 128 отсчетами вектора q. Затем к этому сигналу присоединяется шум с помощью генератора случайных чисел и формируется вектор из 128 отсчетов зашумленного сигнала. Используя прямое БПФ, сигнал с шумом преобразуется из временной области в частотную, которую создает вектор f из 64 частотных составляющих. Затем выполняется фильтрующее преобразование, эффективность которого оценивается параметром фильтрации а. Отфильтрованный сигнал (вектор g) подвергается обратному БПФ и создает вектор выходного сигнала h.

В конце документа (см. рис. 14. 28) сравниваются временные зависимости входного и выходного сигналов. Хотя абсолютной идентичности между ними нет, видно, что выходной сигнал почти повторяет входной и в значительной мере избавлен от высокочастотных шумовых помех, маскирующих полезный сигнал.

Алгоритмы, реализованные в данном примере, находят широкое применение на практике. Они лежат в основе создания фильтров для аналоговых сигналов.

Фильтрация аналогового сигнала с применением БПФ (начало документа)

Рис. 14. 27 Фильтрация аналогового сигнала с применением БПФ (начало документа)

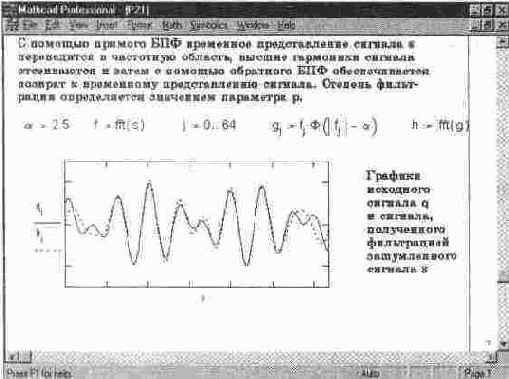
Фильтрация аналоговых сигналов

Под фильтрацией подразумевается выделение полезного сигнала из его смеси с мешающим сигналом — шумов. Наиболее распространенный тип фильтрации — частотная фильтрация. Если известна область частот, занимаемая полезным сигналом, достаточно выделить ее и подавить те области, которые заняты шумом.

Документ на рис. 14. 27 иллюстрирует технику фильтрации с применением БПФ. В начале документа синтезируется двухчастотный сигнал, пред-

Фильтрация пространственного образа (конец документа)

Рис. 14. 32 Фильтрация пространственного образа (конец документа)

Полезно отметить, что графики трехмерной поверхности здесь также получены без применения стандартных средств построения трехмерных поверхностей системы. Поэтому без какой-либо доработки (кроме выбора шрифта комментариев) этот пример можно использовать и в ранних версиях системы MathCAD 2. 0/2. 04, не имеющих средств построения трехмерных фигур (а говоря точнее, он и взят из примеров для этих систем).

Фильтрация пространственного образа (начало документа)

Рис. 14. 31 Фильтрация пространственного образа (начало документа)

Система MathCAD 7. 0 реализует двумерное БПФ, если в операциях БПФ использовать не векторы, а матрицы. Однако у ранних версий MathCAD таких возможностей нет. Поэтому воспользуемся более наглядной реализацией двумерного БПФ с помощью одномерного. На рис. 14. 31 показан документ, реализующий фильтрацию трехмерной поверхности с помощью двумерного БПФ.

В начале документа создается матрица трехмерной поверхности М со случайными отклонениями каждой точки. Внизу слева построена эта поверхность — см. рис. 14. 32. Она имеет вид пятна, в котором отдаленно угадываются общие контуры поверхности. Регулярность расположения точек-крестиков на ней вообще не заметна. В средней части документа показана реализация математического аппарата фильтрации. Рисунок справа внизу документа показывает результат фильтрации. На нем отчетливо видны не только общие формы поверхности (типа "выпуклый лист"), но и явная регулярность расположения точек. Это и есть результат фильтрации.

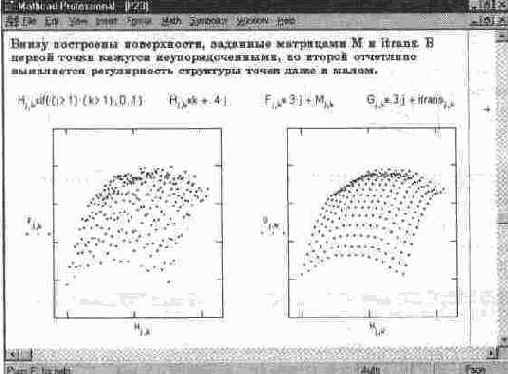
Фильтрация пространственного образа с применением двумерного БПФ

До сих пор мы приводили примеры применения одномерного БПФ. Однако возможно и двумерное преобразование Фурье, позволяющее решать более сложные задачи.

Финансово-экономические расчеты со сложными процентами

Финансово-экономические расчеты со сложными процентами

В наше время перехода к рыночным отношениям финансово-экономические расчеты могут интересовать многих читателей настоящей книги MathCAD не содержит специальных функций для проведения таких расчетов Однако все они легко выполняются встроенными в систему средствами

Документ на рис 147 иллюстрирует наиболее распространенные расчеты с единичным вкладом Все они основаны на применении сложных процентов, и их не так давно (в период государственной монополии на банковские расче ты и стабильных процентов годовых) можно было использовать для оценки финансовой ситуации с нашими вкладами на сберкнижках

Разумеется, вы можете подставить в них те параметры, которые соответствуют текущему положению дел в нашей рыночной экономике

Финансовые операции с начальным и регулярными вкладами

Если вы имели возможность внести некоторый начальный вклад и затем намерены регулярно пополнять его ежегодно N раз, расчеты придется вести по несколько иным формулам. Они приведены в документе на рис. 14. 9.

Здесь особый интерес вызывает последний пример — вычисление процента годовых.

Финансовые операции с регулярными вкладами

Если ваша заработная плата превышает прожиточный минимум, простой жи тейский опыт подсказывает, что лучше не копить деньги "в чулке", а периоди чески (N раз в год) относить их в Сбербанк Документ на рис 148 показывает возможные ситуации при операциях с ежегодными регулярными вкладами

Физические расчеты

14. 7. Физические расчеты

Гармонический синтез меандра

Одним из фундаментальных положений математики, ранее казавшимся абст рактным а затем нашедшим широчайшее практическое применение, является возможность описания любой периодической функции, имеющей конечное число разрывов и непрерывность производных между ними, с помощью три гонометрического ряда Фурье [29, 30]

где k — порядковый номер гармоники, f1 — частота колебания Этот ряд со держит бесконечное число косинусных и синусных составляющих — гармо ник, причем амплитуды этих составляющих а^ и Ь^ являются коэффициента ми Фурье, определяемыми приводимыми несколько позднее интегральными выражениями

Приведенный ряд содержит бесконечное число членов и при таком пред ставлении оказывается бесполезным, поскольку время вычисления в этом случае также равно бесконечности К счастью, амплитуды гармоник для ре альных зависимостей y (t) довольно быстро уменьшаются по мере роста номеpa гармоники k. Поэтому на практике обычно приходится иметь дело с ограниченными по числу гармоник рядами Фурье.

Помимо упомянутой формы ряд Фурье можно представить в виде:

где амплитуда гармоник М^ и их фаза (р^ определяются выражениями:

Преимущество ряда в этой форме в том, что для вычисления каждого члена ряда нужно лишь один раз обращаться к довольно медленному вычислению тригонометрической функции. В дальнейшем будут приведены формулы, позволяющие вычислять коэффициенты Фурье (либо амплитуды и фазы гармоник) для любой функции y (t). Это является задачей спектрального анализа. Здесь же мы рассмотрим обратную задачу — синтеза зависимости y (t) путем вычисления ряда Фурье с ограниченным числом членов.

Теория спектрального анализа и синтеза хорошо развита, и для многих зависимостей y (t) заведомо известны значения коэффициентов Фурье или законы изменения (с частотой или номером гармоники) амплитуд и фаз гармоник. Это позволяет синтезировать наиболее распространенные зависимости y (t).

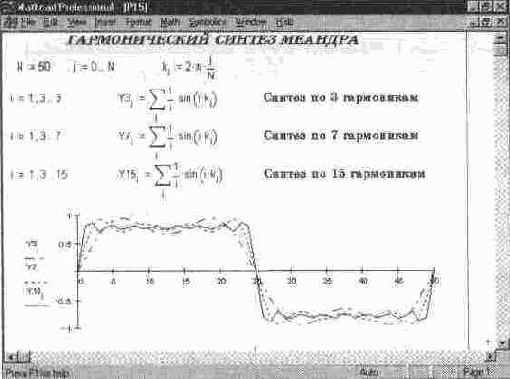
Гармонический синтез меандра

Рис. 14. 18 Гармонический синтез меандра

Документ, представленный на рис. 14. 18, реализует синтез периодических прямоугольных импульсов со скважностью, равной 2 (меандра). Ряд Фурье для таких импульсов содержит только синусные члены, причем лишь с нечетными k. Это упрощает синтез, который в документе реализован для 3, 7 и 15 гармоник.

Меандр — не самая удачная для синтеза зависимость, поскольку он содержит резкие скачки. Для не очень сведущего в математике пользователя

удивительно, что такого рода зависимость вообще синтезируется из синусоид, которые представляют собою гладкие функции без всяких скачков Естественно, что для получения скачков нужно брать очень большое число гармоник Тем не менее уже при 15 гармониках синтезированный сигнал напоминает меандр и отличается от него конечным временем перепада и характерной волнистостью Она усиливается после быстрых перепадов и является проявлением так называемого эффекта Гиббса [30].

Эффект Гиббса, к сожалению, невозможно устранить (и даже ослабить) лишь увеличением числа гармоник при синтезе В этом случае просто возрастает частота волнообразных колебаний, но их относительная амплитуда меняется незначительно — она доходит до 18% от амплитуды синтезируемых колебаний.

Эффект Гиббса — явление крайне нежелательное Он фактически вводит в синтезируемые колебания новые компоненты, на деле отсутствующие Это может замаскировать или сильно исказить компоненты колебания, которые интересуют исследователя. Поэтому обычно стремятся ослабить эффект Гиббса, даже за счет уменьшения точности синтеза В дальнейшем будут обстоятельно рассмотрены приемы ослабления этого эффекта

Гармонический синтез пилообразных колебаний

В литературе можно найти множество примеров разложения в ряд Фурье самых разнообразных зависимостей y (t) Используя приведенные для них значения коэффициентов Фурье, можно синтезировать самые разнообразные за висимости (сигналы) Еще одним примером может служить показанный на рис. 14 19 гармонический синтез треугольных колебаний

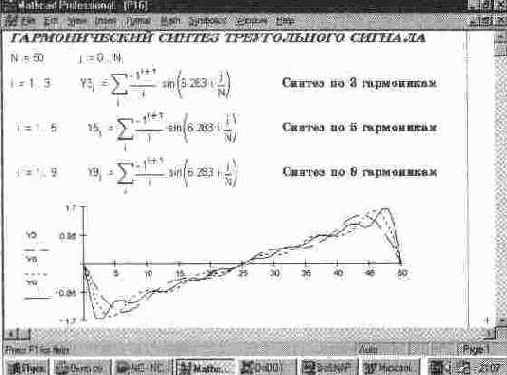
Гармонический синтез треугольных колебаний

Рис. 14. 19 Гармонический синтез треугольных колебаний

Может возникнуть вполне закономерный вопрос зачем столь сложным способом синтезировать такие простые зависимости, если они легко описываются целиком или по частям с помощью простых аналитических выражений? Действительно, если нужно просто смоделировать сигнал как временную функцию, нет необходимости синтезировать его по множеству гармоник

Однако существует большое количество теоретических методов анализа сигналов и практических устройств, основанных именно на спектральном подходе. Примером могут служить частотные фильтры и даже целые радиотехнические системы. При их анализе сигнал y (t) часто приходится разлагать в ряд Фурье для проведения в дальнейшем операций с гармониками. Имея сигнал y (t) уже в виде гармоник, можно заметно сократить время обработки сигнала и вообще убрать этап задания функции в виде временной зависимости. Во многих странах до сих пор выпускаются синтезаторы сложных колебаний, основанные на суммировании их гармонических составляющих с разными амплитудой и фазой.

График функции Розенброка (окончание документа, представленного на рис. 14. 12)

Рис. 14. 13 График функции Розенброка (окончание документа, представленного на рис. 14. 12)

Поиск задается вычислительным блоком, открываемым словом Given. Фактически решается система уравнений. Два уравнения после слова Given приближенно задают условия минимума, третье уравнение (с функцией minегг) отыскивает решение, в максимальной степени удовлетворяющее заданным условиям минимума.

Функция Розенброка имеет очевидные значения х=у=\ в точке минимума. Графическое представление функции напоминает овраг (см. рис. 14. 13), что затрудняет поиск минимума рядом простых методов.

Следует отметить, что тут заведомо известно, что функция имеет минимум. Если бы этого не было, пришлось бы ввести условия на значения вторых производных функции по каждой переменной.

Интегрирование таблично заданных функций

Часто возникает необходимость в вычислении определенного интеграла для таблично заданной функции. Тогда прямое применение встроенного в систему оператора вычисления интеграла оказывается невозможным, так как он предполагает задание подынтегральной функции в аналитическом виде.

Документ на рис. 14. 11 иллюстрирует три способа вычисления определенного интеграла при табличном задании подынтегральной функции. Первые два способа (методом трапеций и Симпсона) используют довольно хорошо известные формулы интегрирования табличных данных. Третий способ использует встроенный оператор вычисления интеграла. При этом таблично заданная функция интерполируется линейной зависимостью или набором сплайновых функций (полиномов третьей степени).

Интегрирование табличных данных

Рис. 14. 11 Интегрирование табличных данных

В качестве исходных данных взяты ординаты квадратичной параболы, что позволяет вычислить интеграл без этих ухищрений. Такое вычисление представлено для контроля в конце документа. Нетрудно заметить, что лишь интегрирование методом Симпсона и интегрирование со сплайн-интерполяцией дают полное совпадение с прямым интегрированием (не стоит забывать, что установленный формат цифровых данных выводит результат только с шестью значащими цифрами после десятичной точки).

Интерполяция по общей формуле Лагранжа

В этом пакете рассматриваются функции одной переменной вида у (х), как правило, заданные в табличном виде, т. е. рядом значений х и соответствующих им значений у. Именно так обычно задаются данные эксперимента, получаемые на различных физических или электронных измерительных установках.

Важной задачей математической обработки подобных данных является и их представление в виде некоторой математической зависимости, допускающей проведение над нею обычных математических операций, например вычисление у (х) при х, не совпадающих с исходными (узловыми) точками, интегрирование или дифференцирование функций, проведение их статистической обработки (сглаживания или фильтрации) и т. д.

Одной из самых распространенных задач такого рода является ингерпо-ляция таблично заданных функций, т. е. вычисление их значений в промежутках между узловыми точками. В математической литературе общепринято представление многих специальных функций в виде математических таблиц [14], ориентированных на интерполяцию по заданному числу узловых точек (обычно от 2 до 6).

В систему MathCAD встроены функции линейной и сплайн-интерполяции, при которых отдельно на каждом промежутке функция представляется отрезком прямой или кубическим многочленом. Последний вычисляется так, чтобы обеспечить стыковку в узловых точках как значений функции, так и ее первых двух производных (что и дает необходимую гладкость графика функции).

Эти мощные средства интерполяции имеют, однако, существенный недостаток: параметры интерполирующей функции различны на различных участках интерполяции. Другими словами, такая интерполяция не может быть сведена к одной интерполирующей формуле, что затрудняет интерполяцию математических таблиц, за исключением линейной интерполяции, дающей довольно низкую точность.

На рис. 14. 14 представлен документ, задающий обобщенную формулу интерполяции методом Лагранжа. Эта формула синтезирует полином Лагранжа, используя два вектора: с координатами xi и yi узловых точек. Преимущества такого подхода в том, что число узловых точек и их расположение может быть любым (в том числе неравномерным), а для интерполяции используется единая интерполирующая формула f (x), к сожалению, довольно сложная.

При интерполяции полиномом Лагранжа степень полинома п однозначно связана с числом узловых точек. Она на единицу меньше этого числа Значения ординат интерполирующей функции в узловых точках совпадают со зна-

Интерполяция табличных данных по формуле Лагранжа

Рис. 14. 14 Интерполяция табличных данных по формуле Лагранжа

чениями ординат узловых точек, поэтому график интерполирующей функции f (x) точно проходит через эти точки. К сожалению, при высокой степени полинома (более 5—6) погрешность вычислений его значений заметно возрастает, поэтому выбор п выше 6 на практике нецелесообразен. А это означает, что функция у (х) должна быть представлена небольшим числом достаточно точных значений.

К недостаткам интерполяции по обобщенной формуле Лагранжа относится и довольно большое время вычислений, поскольку формула интерполяции далеко не проста.

Конец документа, иллюстрирующего решение дифференциального уравнения методом Рунге Кутта

Рис. 14. 17 Конец документа, иллюстрирующего решение дифференциального уравнения методом Рунге Кутта

Рассматривая рис 14 17, нетрудно сделать вывод о наглядности реализа ции метода Рунге — Кутта По существу приведенные уравнения повторяют известные формулы этого метода часто встречающиеся в учебной литературе по численным методам решения дифференциальных уравнений

Линейное сглаживание по пяти точкам

Один из полезных видов статистической обработки функции у (х), заданной п точками, заключается в статистической обработке каждой точки с учетом положения нескольких ближайших точек. Например, простейший способ такой обработки усредняет значения этой точки и нескольких других, окружающих ее слева и справа. В результате будет получен вектор ys сглаженных значений у (х). Некоторую проблему представляет вычисление сглаженных значений точек, примыкающих к концевым, но можно вывести формулы сглаживания и для этих точек.

MathCAD 7 О PRO имеет встроенную функцию сглаживания Однако полезно проверить работу известных алгоритмов сглаживания по ряду точек. Так, линейное сглаживание по пяти точкам демонстрируег документ, показанный на рис. 14. 15. На нем вначале задан вектор параболической зависимости, на которую наложены сильные случайные компоненты, создаваемые генератором случайных чисел. Далее заданы пять формул сглаживания: по две для крайних двух точек слева и справа и одна для других (эта формула просто находит среднее значение для центральной точки и окружающих ее четырех ближайших точек). Фактически кривая сглаживания состоит из ряда отрезков прямых линий, откуда и название — линейное сглаживание.

На приведенном рисунке видно, что сглаженная кривая проходит внутри облака точек и неплохо вписывается в него. При этом число сглаженных точек равно числу исходных точек (в нашем случае их 50) Разумеется, при таком большом числе сглаженных точек эффективность сглаживания оказывается заметно ниже, чем, например, при проведении регрессии с большим числом исходных точек

Линейное сглаживание по пяти точкам

Рис. 14. 15 Линейное сглаживание по пяти точкам

Можно повысить эффективность сглаживания, увеличивая число точек, используемых для статистической обработки заданной точки, и перейдя к кривой сглаживания в виде отрезка полинома более высокой степени, чем 1 Так, известны формулы нелинейного сглаживания по семи точкам [1, 2, 28] Этих формул семь по три для крайних точек и одна для остальных Для нели нейных зависимостей, близких к параболическим или содержащих отрезки парабол, нелинейное сглаживание гораздо более эффективно, чем линейное Тем не менее и здесь гладкость кривой сглаживания невелика

Единого мнения о целесообразности повторения процедуры сглаживания у математиков нет Одни считают, что повторное сглаживание делает кривую сглаживания более плавной Другие не рекомендуют применение повторного сглаживания В целом сглаживание — эффективный инструмент предварительной обработки исходных данных Затем можно использовать более тонкие методы их обработки, например фильтрацию на основе спектрального анализа и синтеза, полиномиальную регрессию с применением полинома определенного порядка и т д

Моделирование генератора гармонических колебаний на туннельном диоде

Пусть туннельный диод подключен к источнику постоянного напряжения Е через последовательно соединенные резистор R и индуктор L. Пусть далее R и Е выбраны так, что рабочая точка туннельного диода находится на падающем участке N-образной ВАХ туннельного диода. Это обстоятельство принципиально важно, поскольку дифференциальная малосигнальная проводимость туннельного диода тогда является отрицательной. Физически это означает, что туннельный диод отдает энергию во внешнюю цепь.

Если учесть емкость С туннельного диода (совместно с емкостью монтажа и нагрузочной емкостью), такая схема будет описываться следующей системой нелинейных дифференциальных уравнений [6, 8]:

Нелинейность этой системы обусловлена тем, что во втором уравнении ток туннельного диода 1 (и) нелинейно зависит от напряжения на нем и емкости С. Зависимость 1 (и) есть N-образная вольт-амперная характеристика туннельного диода.

Документ на рис. 14. 44 позволяет рассчитать переходные процессы при включении рассмотренной схемы таблично заданной JV-образной ВАХ туннельного диода. Она задается своими табличными значениями — элементами векторов U и I. N-образная ВАХ получается сплайн-интерполяцией с кубической экстраполяцией Решение системы дифференциальных уравнений обеспечивается методом Эйлера

Моделирование генератора на туннельном диоде (конец документа)

Рис. 14. 45 Моделирование генератора на туннельном диоде (конец документа)

Следует отметить, что область применения описанного документа неизмеримо шире, чем моделирование конкретной схемы генератора на туннельном диоде Практически с его помощью можно моделировать основную цепь на любом приборе с N- или N-образной ВАХ (например, индуктивный релак сатор на лавинном транзисторе, генераторы на N- и Л-диодах и транзисторах, их аналогах и т д) Достаточно лишь задать данные их ВАХ и соответствующие исходные данные

Стоит, к примеру, уменьшить емкость С в два-три раза, а индуктивность увеличить, как генератор перейдет в режим генерации релаксационных коле баний Этот случай показан на рис 14 46

Теперь возникают более резкие колебания, фазовый портрет начинается сразу с предельного цикла, форма которого принципиально отличается от эллиптической Соответственно, сильно отличаются от гармонической и форма напряжения на туннельном диоде, и форма тока, текущего через резистор R Колебания при этом относятся к типу релаксационных и возникают сами по себе, без какого-либо внешнего воздействия Практически после первого цикла колебаний устанавливается их стационарный режим

Еще более интересные результаты можно получить, используя импульсное питание цепи на туннельном диоде Тут напряжение питания можно задать зависимостью ei (t) в виде прямоугольно! о импульса, наложенного на постоянное напряжение — пьедестал. Напряжение выбирается так, что рабочая точка попадает на первую восходящую ветвь N-образной ВАХ и оказывается стабильной. При этом цепь устойчива и колебания не генерируются. При появлении импульса рабочая точка попадает на падающий участок и развивается процесс генерации одного полного цикла колебаний. Цепь, таким образом, выполняет функции ждущего релаксационного генератора. Читатель может самостоятельно изменить документ для реализации этого режима работы.

Моделирование генератора на туннельном диоде (начало документа)

Рис. 14. 44 Моделирование генератора на туннельном диоде (начало документа)

Результаты моделирования (см рис 14 45) в этом документе представлены в двух формах Первая имеет вид фазового портрета — положение каждой точки решения отмечается на графике в плоскости ВАХ Для чисто гармонических колебаний предельный цикл колебаний на фазовой плоскости должен иметь форму эллипса Его отличие от эллипса небольшое, что, с одной стороны, говорит о заметном влиянии нелинейности, а с другой — о почти гармоническом характере колебаний Вторая форма — временные зависимости напряжения на туннельном диоде и тока в цепи резистора R Эти зависимости близки к гармоническим

Моделирование падения парашютиста (начало документа)

Рис. 14. 38 Моделирование падения парашютиста (начало документа)

дифференциальных уравнений и требует учета сопротивления воздушной среды до и после открытия парашюта. В документе на рис. 14. 38 показано выполнение этого моделирования с применением конечно-разностного метода решения.

Начало документа, иллюстрирующего решение дифференциального уравнения методом Рунге — Кутта

Рис. 14. 16 Начало документа, иллюстрирующего решение дифференциального уравнения методом Рунге — Кутта

Документ на рис. 14. 16 состоит из двух частей. Первая часть (она и показана на рисунке) содержит ввод исходных данных и вывод графика решения. Для решения надо задать функцию f (x, y), начальное (startx) и конечное (endx) значения х, число точек решения п и начальное значение (inity) переменной у. При построении графика функции указываются нижний (L) и верхний (U) пределы изменения искомой зависимости у (х).

Вторая часть документа (см. рис. 14. 17) в действительности располагается справа от первой части и размещается в обычно невидимой части документа Поэтому пользователь избавлен от созерцания тривиальных или просто не интересующих его математических формул и может сосредоточить внимание лишь на вводе исходных данных и функции f (x, y) и выводе результатов

Общие замечания

14. 1. Общие замечания

В этой главе описаны наиболее интересные примеры из десяти пакетов при менений систем MathCAD, размещенных на дискете, прилагаемой к книге [б]. Примеры охватывают решения широкого круга практических задач в об ласти математики, физики, электро- и радиотехники, электроники [20-39].

В педагогической среде нередко звучат нарекания, что в системах Math CAD скрыты методы реализации численных расчетов и потому последние не наглядны. Такие нарекания абсурдны, поскольку именно MathCAD позволя ет описать алгоритм любого численного метода на естественном математичес ком языке, не прибегая к таким (скорее программистским, чем математичес ким) понятиям, как условные переходы, циклы и т. д. (хотя реализация алгоритмов с ними также возможна с помощью аппарата ранжированных пе ременных, не говоря уже о применении программных блоков).

При подготовке описанных здесь примеров определенное внимание уде лялось реализации численных методов типовыми возможностями системы MathCAD, причем даже тех методов, которые реализованы встроенными функциями систем. Это, во-первых, демонстрирует возможности системы MathCAD в наглядной реализации таких методов, во-вторых, позволяет ре шать относящиеся к ним задачи с использованием тех версий системы, у ко торых соответствующих функций нет, а в-третьих, дает заметное ускорение вычислении.

Разбор описанных примеров позволит читателю существенно углубить свои знания о возможностях систем класса MathCAD и полнее использовать их в своей учебе, на практике и в научном творчестве, а также заметно умень шить затраты времени на освоение системы, поскольку избавит вас от необхо димости самостоятельно придумывать учебные примеры.

Операции с начальным и регулярными ежегодными вкладами

Рис. 14. 9 Операции с начальным и регулярными ежегодными вкладами

Падение парашютиста \

Рассмотрим существенно более сложный случай динамического движения:

на высоте уО из самолета выпрыгивает парашютист и в свободном полете падает вниз. Спустя пять секунд он дергает кольцо и испытывает заметные перегрузки из-за раскрытия парашюта и резкого снижения скорости падения. Моделирование падения основывается на решении нелинейной системы

Параметрическая трехмерная графика

14. 2. Параметрическая трехмерная графика

При построении трехмерных поверхностей и объемных фигур можно использовать параметрическое задание описывающих их функций. Фигуры задаются значениями координат х, у и z всех точек фигуры. При этом в шаблоне 3D-графики указываются три матрицы, хранящие массивы этих координат, — X, Y и Z. Ниже представлены интересные примеры применения такой графики.

Поиск минимума функции Розенброка

С помощью функции minerr возможен поиск экстремума и функций ряда переменных. Типичной тестовой функцией двух переменных является функция Розенброка, обычно применяемая для тестирования программ минимизации функций ряда переменных. На рис. 14. 12 показан поиск минимума функции Розенброка с применением функции minerr.

Поиск минимума тестовой функции Розенброка

Рис. 14. 12 Поиск минимума тестовой функции Розенброка

Построение АЧХ и ФЧХ линейной системы по ее операторной характеристике (начало документа)

Рис. 14. 40 Построение АЧХ и ФЧХ линейной системы по ее операторной характеристике (начало документа)

В этом документе представлено также построение по операторной функции передаточной характеристики системы. Для каждого значения времени t эта характеристика определяется интегралом с бесконечным пределом интегрирования:

На рис. 14, 41 показано построение переходной характеристики.

Построение фигуры — узлов, образованных толстыми "канатами" (начало документа)

Рис. 14. 5 Построение фигуры — узлов, образованных толстыми "канатами" (начало документа)

Сама фигура, построенная по алгоритму, представленному на рис 145, изображена на рис 146

Построение фигуры вращением линии вокруг оси Х

Построение фигуры вращением линии вокруг оси Х

Интересные объемные фигуры можно получить, вращая некоторую кривую вокруг той или иной оси. При этом необходимо обеспечить пересчет координат всех узловых точек фигуры по известным из геометрии формулам. На рис. 14. 2 показано построение такой фигуры вращением линии, заданной функцией f (x), вокруг оси X.

В документе на рис. 14. 2 приведены все необходимые формулы для пересчета координат узловых точек фигуры при ее вращении. Даны также графики исходной кривой (слева внизу) и фигуры, полученной ее вращением (справа внизу). Фигура напоминает опрокинутую рюмку, лежащую на плоскости. Она построена без применения функциональной окраски, но с использованием алгоритма удаления невидимых линий.

Построение фигуры вращением линии вокруг оси Y

Таким же способом можно построить фигуру, полученную вращением исходной кривой вокруг оси Y. Это демонстрирует документ, показанный на рис. 14. 3.

Чтобы показать возможности задания различного стиля рисунков, в нашем случае фигура построена с удалением невидимых линий каркаса и с при-

Построение фигуры вращением линии вокруг оси Y

Рис. 14. 3 Построение фигуры вращением линии вокруг оси Y

менением функциональной окраски. Нетрудно заметить, что это делает фигуру очень наглядной.

Построение фигуры вращением линии вокруг осиХ

Рис. 14. 2 Построение фигуры вращением линии вокруг осиХ

Построение графика объемной спирали

3D Scatter Plot — вид трехмерных графиков, особенно удобный для представления пространственного расположения множества мелких объектов, условно называемых точками. На рис. 14. 4 показано применение этого графика для построения 100 точек, лежащих на пространственной спирали, напоминающей растянутую пружину.

Для каждой точки в этом случае необходимо располагать тремя координатами — X, Y и Z. Их совокупность образует три одноименных вектора. Вви-

Построение графика вида 3D Scatter Plot для точек пространственной спирали

Рис. 14. 4 Построение графика вида 3D Scatter Plot для точек пространственной спирали

ду простоты алгоритма построения необходимости в более подробном его описании нет. Заметим лишь, что число точек N можно менять.

Построение переходной характеристики (конец документа, представленного на рис. 14. 40)

Рис. 14. 41 Построение переходной характеристики (конец документа, представленного на рис. 14. 40)

К счастью, у всех реальных систем АЧХ на высоких частотах имеет спад и при больших w>wmax принимает близкие к нулю значения. В нашем примере это происходит уже при w>5, что позволяет заменить бесконечный предел интегрирования на конечный.

Вычисление h (t) в документе на рис. 14. 42 выполнено по этому алгоритму. Число 0. 637 перед знаком интеграла есть значение 2/тс. Рядом с графиком h (t) выведена таблица времен t и значений h (t). Анализируемая цепь является цепью 2-го порядка и имеет соответствующие признаки заметно демпфированной цепи 2-го порядка — характерный подъем АЧХ на некоторой частоте и переходную характеристику с небольшим выбросом.

Построение пространственной фигуры — узлов, образованных толстыми "канатами"

О больших возможностях графики MathCAD PLUS 7. 0 PRO свидетельствует пример, приведенный на рис. 14. 5. Он же иллюстрирует применение типовых матричных функций для описания и пространственного преобразования сложной трехмерной фигуры — узлов, образованных толстыми "канатами".

Построение сферы

На рис. 14. 1 показано построение в трехмерном пространстве сферы. Сфера строится из каркаса, причем число деления ее по вертикали N задается в начале построения. Затем вычисляются массивы опорных точек каркаса, которые представлены матрицами X, Y и Z.

Построение сферы

Рис. 14. 1 Построение сферы

Используя различные форматы 3D-графиков, можно выполнить рисунок сферы в различных стилях, в том числе с цветной или черно-белой окраской. Однако в таком случае каркасное построение с применением алгоритма удаления невидимых линий дает, пожалуй, наиболее наглядное представление о характере этой простой объемной фигуры. На рис. 14. 1 представлено два варианта построения сферы с применением различной функциональной окраски.

Параметрическое задание трехмерной поверхности позволяет эффективно применять форматирование их графиков, в частности задавая углы обзора 3D-фигур и меняя их функциональную окраску. К тому же визуализацию таких фигур можно существенно улучшить.

Потеря автомобилем энергии при торможении

Услышав визг тормозов автомобиля, мы с ужасом следим, сумеет ли он сбросить скорость и не настигнет ли нас до того, как мы успеем отскочить Полезно (скорее шоферу, чем нам) знать, как быстро автомобиль теряет энергию при торможении Решение этой задачи для автомобиля с дисковым тормозным устройством представлено на рис 14 35

Преодоление самолетом звукового барьера

Большинство из нас слышали в ясную погоду звуки, напоминающие гром. Почти наверняка это были либо отзвуки дальней грозы, либо грохот, создаваемый самолетом при преодолении звукового барьера. В физике известна функция М (и, h), определяющая так называемое число Маха, зависящее от скорости самолета и и высоты полета h [32]. В момент преодоления звукового барьера значение М (и, h) становится равным 1. Скорость, на которой преодолевается этот барьер, падает с увеличением высоты полета.

Документ на рис. 14. 33 содержит определение функции М (и, h). На верхнем графике показаны зависимости М (и, h) от и для четырех значений h, а также уровень единицы. Звуковой барьер преодолевается в момент, когда соответствующая зависимости М (и, h) кривая пересекает уровень единицы.

Пример генерации релаксационных колебаний

Рис. 14. 46 Пример генерации релаксационных колебаний

Приведенные выше примеры наглядно показывают, что даже незначительное изменение параметров одной и той же цепи на туннельном диоде способно резко (и даже качественно) изменить режимы ее работы. При этом цепь может выполнять практически любую функцию электронного устройства: нелинейного преобразователя, усилителя и генератора гармонических колебаний, автоколебательного и ждущего релаксатора и триггера.

Примеры расчетов с единичными вкладами и сложными процентами

Рис. 14. 7 Примеры расчетов с единичными вкладами и сложными процентами

Примеры расчетов с регулярными вкладами

Рис. 14. 8 Примеры расчетов с регулярными вкладами

При таких операциях, разумеется, не имеет значения, какие деньги вы вкладываете (рубли, марки или доллары). Главное, чтобы это были какие-то одни денежные единицы

Расчет движения снаряда

Пусть спортсмен мечет снаряд (например, диск или ядро) с некоторой начальной скоростью VO и под углом Q к горизонту. По какой траектории происходит полет снаряда, если пренебречь сопротивлением воздуха? Ответ общеизвестен — по параболической Однако мы попытаемся ответить на этот вопрос моделированием движения, решая систему описывающих его дифференциальных уравнений численным методом Эйлера Этот подход иллюстрирует документ на рис. 14. 37.

Расчет отклика системы на воздействие, заданное таблично

Расчет отклика линейной системы с произвольной формой переходной характеристики на произвольно заданное входное воздействие — задача достаточно сложная. Ее решение облегчается, если передаточная характеристика и входное воздействие заданы в табличном виде, т. е. в виде ряда значений a (t) и u (t) для фиксированных моментов времени t на отрезке Т. Наличие в системе MathCAD эффективного аппарата сплайн-интерполяции табличных данных позволяет с блеском решить такую задачу.

Документ на рис. 14. 42 иллюстрирует сказанное. Векторы А и U в нем задают узловые точки зависимостей a (t) и u (t) на отрезке времени Т. Эти векторы должны быть одинаковой длины, а их элементы должны относиться к соответствующим одинаковым моментам времени. Далее проводится сплайн-интерполяция (с линейной экстраполяцией) зависимостей aft) и u(t), что позволяет получить эти зависимости в непрерывном виде и использовать в интеграле свертки для вычисления реакции y (t).

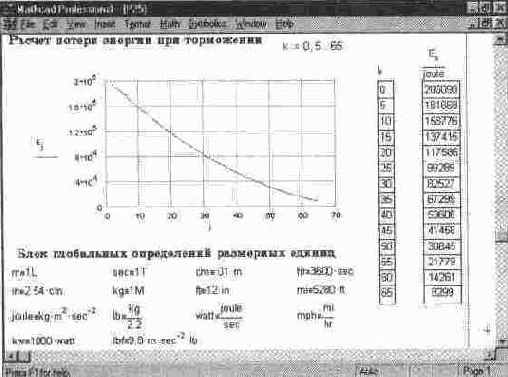
Расчет потери энергии тормозящим автомобилем (конец документа)

Рис. 14. 36 Расчет потери энергии тормозящим автомобилем (конец документа)

Процесс потери энергии в общем случае связан с решением нелинейного дифференциального уравнения. Физики любят использовать для такого решения простые конечно-разностные методы, при которых решение выражается рекуррентной формулой. Фактически эти методы соответствуют решению простым методом Эйлера. Результаты решения представлены на рис. 14. 36.

Важно отметить, что в данном расчете используются размерные величины (энергия определяется в джоулях). Для расчетов с размерными величинами в состав MathCAD входят файлы, содержащие глобальные определения этих величин. В конце документа (на рис 14. 36) показан пример использования такого файла. В нем содержится определение многих размерных величин, относящихся к физике (их больше, чем это нужно для нашего конкретного примера).

Расчет потери энергии тормозящим автомобилем (начало документа)

Рис. 14. 35 Расчет потери энергии тормозящим автомобилем (начало документа)

Расчет реакции системы на заданное воздействие (конец документа)

Рис. 14. 43 Расчет реакции системы на заданное воздействие (конец документа)

Расчет реакции системы на заданное воздействие Сначапо документа)

Рис. 14. 42 Расчет реакции системы на заданное воздействие Сначапо документа)

Табличное задание u (t) облегчает вычисление производной i/(t) в численном виде, что, в свою очередь, ускоряет вычисления. Обратите внимание, что здесь и' — имя функции пользователя, вычисляющей значение производной численным методом. В конце документа (см рис. 14. 43) построены графические зависимости aft), u (t) и y (t).

Расчет скорости преодоления самолетом звукового барьера (конец документа)

Рис. 14. 34 Расчет скорости преодоления самолетом звукового барьера (конец документа)

Более полезно не просто знать саму по себе зависимость М (и, h), а из условия М (и, h) =i получить зависимость скорости преодоления звукового барьера u (h) от высоты h. Для этого можно воспользоваться функцией поиска корня указанного условия. Это также сделано в конце документа (см. рис. 14. 34).

Этот пример дает наглядное представление о решении простых физичес ких задач, базирующихся на уравнениях теоретической физики, и демонстриру ет возможность находить с помощью MathCAD корень нелинейных уравнений

Расчет скорости преодоления самолетом звукового барьера (начало документа)

Рис. 14. 33 Расчет скорости преодоления самолетом звукового барьера (начало документа)

Расчет траектории и угла наклона летящего снаряда

Рис. 14. 37 Расчет траектории и угла наклона летящего снаряда

Обратите внимание, что операции (как это принято в физических расче тах) происходят с размерными величинами. В результате моделирования получены траектория движения снаряда (зависимость высоты от расстояния по горизонтали), а также зависимость угла наклона траектории от расстояния по горизонтали. Как и следовало ожидать, траектория полета снаряда оказалась параболической.

Реализация цифровой фильтрации (конец документа)

Рис. 14. 30 Реализация цифровой фильтрации (конец документа)

Заметим, что в данном примере речь идет не о фильтрации сигнала на фоне шумов, а о прохождении сложного составного сигнала через цифровые фильтры. Графики в конце документа иллюстрируют характер искажений сигнала при этом.

Реализация цифровой фильтрации (начало документа)

Рис. 14. 29 Реализация цифровой фильтрации (начало документа)

Решение дифференциального уравнения первого порядка методом Рунге — Кутта

Решение дифференциальных уравнений широко применяется в практике научно-технических расчетов Это связано с тем, что дифференциальные уравнения (и системы из них) описывают поведение различных объектов в динамике, например переходные процессы в электронных схемах или работу часового маятника Линейные дифференциальные уравнения имеют решения в виде специальных функций (скажем, функций Бесселя) Однако многие физические системы нелинейны и описываются нелинейными дифференциальными уравнениями, не имеющими аналитического решения. В этом случае приходится использовать численные методы решения дифференциальных уравнений.

Версия MathCAD 7. 0 PRO содержит мощные средства для реализации численных методов решения дифференциальных уравнений. Поэтому может возникнуть вопрос: а нужно ли создавать свои документы для реализации таких методов? Ответ на него не однозначен. Если ваша цель — решение конкретной задачи, то проще воспользоваться готовыми функциями MathCAD. Они были описаны выше. Однако нередко педагоги и специалисты без должных оснований говорят о трудности реализации в системе MathCAD обычных численных методов. Это неверно! Реализация таких методов в системе MathCAD легка и наглядна. Более того, она позволяет вмешиваться в алгоритмическую реализацию методов решения, что способствует созданию новых или улучшенных методов решения дифференциальных уравнений, ориентированных на решение интересующих пользователя задач.

Здесь мы остановимся на реализации решения дифференциального уравнения i/=f (x, y) хорошо известным методом Рунге — Кутта. Пусть h — шаг приращения переменной х, i — индекс, имеющий значения от 1 до N (N — число интервалов решения с шагом h). Метод Рунге — Кутта четвертого порядка дает погрешность решения порядка h (4, что удовлетворяет самым при-щрчивым требованиям к точности численных методов. Он неоднократно подробно описывался в [6, 8, 14]. Его реализация показана на рис. 14. 16.

Синтез исходного сигнала по результатам...

Рис. 14. 24 Синтез исходного сигнала по результатам вычисления его спектра (конец документа, приведенного на рис. 14. 23)

Если умножить значение амплитуды каждой k-й. гармоники на множитель sin ( (k/N)/((k/N), это будет фактически означать переход от формул интегрирования методом прямоугольников к формулам интегрирования методом трапеций — с применением линейной интерполяции y (t). Само по себе это, как отмечалось выше, не является основанием к существенному повышению точности вычислений. Однако такой подход дает заметное ослабление эффекта Гиббса. Рекомендуем читателю проверить это самостоятельно.

Хотя коррекция предполагает, что в формулах интегрирования применяется линейная или квадратичная интерполяция между узлами, по-прежнему используются и дискретные отсчеты, соответствующие исходному вектору Yi. Поэтому максимальное число гармоник, как и ранее, не может превосходить N/2.

Спектральный анализ и синтез с прямой линейной интерполяцией функции между узлами

Вместо того чтобы вводить корректирующие множители, имитирующие интерполяцию функции y (t) между узлами, можно прямо ввести такую интерполяцию. Тогда появляется возможность задавать произвольное число отсчетов y (t) по интерполируемой функции и получить сколь угодно большое число гармоник для ее синтеза. Впрочем, надо помнить, что интерполируемая функция идеально точно совпадает с исходной только тогда, когда число отсчетов равно числу узлов.

В других случаях отсчеты берутся с несколько иной функции, но на практике весьма близкой к исходной. Несмотря на эти оговорки, такой прием дает блестящие результаты: при достаточно большом числе выбранных для синтеза гармоник синтезируемая функция повторяет исходную, а эффект Гиббса исчезает почти полностью.

На рис. 14. 25 показана реализация этого метода. За счет отказа от умножения на 0.

Спектральный анализ методом Берга

Для некоторых простых зависимостей y (t) амплитуды гармоник могут выражаться аналитически. Примером служат отрезки синусоиды, получаемые выделением только верхней ее части. На практике такие колебания широко используются в радиотехнике, где обрезание нижней части синусоиды обусловлено работой электронных приборов (например, ламп или транзисторов) в нелинейном режиме.

Доля периода синусоиды, используемой для анализа гармоник, оценивается углом отсечки 9 (далее он измеряется в радианах). Он, к примеру, равен к, если обрезается нижняя половина синусоиды. Удобно вычислять относительную амплитуду k-тл гармоники (по отношению к усеченной амплитуде синусоидального импульса). Этот параметр для разных k впервые был вычислен Бергом.

Спектральный анализ методом Берга

Рис. 14. 20 Спектральный анализ методом Берга

В документе на рис. 14. 20 представлены формулы для вычисления коэффициентов Берга о. О (относительная постоянная составляющая сигнала), а. 1 (относительная амплитуда первой гармоники) и сот (относительная амплитуда п-й гармоники). Коэффициенты Берга являются функциями угла отсечки.

График в нижней части этого документа дает наглядное представление об изменении первых четырех коэффициентов Берга с изменением угла отсечки.

Нетрудно заметить существование максимумов у этих зависимостей. Например, максимальная амплитуда первой гармоники будет достигнута при угле отсечки 120 градусов, второй гармоники — 60 градусов и т. д. Знать эти углы полезно при проектировании умножителей частоты (например, удвоителей или устроителей), работа которых основана на фильтрации одной из высших гармоник.

Спектральный анализ прямоугольного импульса с применением БПФ

Встроенные в систему MathCAD средства быстрого преобразования Фурье (БПФ) существенно упрощают процедуру приближенного спектрального анализа. БПФ — быстрый алгоритм переноса сведений о функции, заданной 2" отсчетами во временной области, в частотную область. Если речь идет о спектральном анализе функции y (t), ее нужно задавать действительными отсчетами и использовать функцию fft (V), где V — вектор, элементы которого хранят отсчеты функции y (t). Результатом будет также вектор А с комплексными элементами — отсчетами в частотной области (их вдвое меньше, чем отсчетов во временной области). Фактически действительная и мнимая части этого вектора есть коэффициенты Фурье а^ и Ъ^ что существенно упрощает их получение.

Документ на рис. 14. 21 поясняет проведение спектрального анализа с применением функции fft прямого БПФ. В начале документа (левый верхний угол) задан вектор с восемью единичными отсчетами и с остальными (всего их 32) — нулевыми. Затем вычислен вектор А — результат БПФ.

Спектральный анализ прямоугольного импульса с применением БПФ (конец документа)

Рис. 14. 22 Спектральный анализ прямоугольного импульса с применением БПФ (конец документа)

Казалось бы, наличие встроенных средств широко рекламируемого БПФ должно означать ориентацию спектрального анализа на их применение. Но это не так. БПФ имеет ряд серьезных недостатков: неясный для пользователя алгоритм, отсутствие средств подавления эффекта Гиббса и строгая привязка числа отсчетов y (t) к величине 2n (т. е. 2, 4, 8, 16, 32 и т. д.). БПФ дает хорошие результаты, когда взаимное преобразование (прямое и обратное) происходит без ограничения употребляемого при нем количества гармоник. Эти недостатки могут оказаться весьма существенными при проведении спектрального анализа и синтеза, когда наглядность их реализации принципиально важна.

Спектральный анализ прямоугольного импульса с применением БПФ (начало документа)

Рис. 14. 21 Спектральный анализ прямоугольного импульса с применением БПФ (начало документа)

В заключение (см. рис. 14. 22) вычислены амплитуды гармоник и их фазы для представления импульса рядом Фурье. Завершает документ построение графиков амплитуд (модулей) и фаз первых десяти гармоник.

Чтобы лучше понять закономерности спектрального анализа, целесообразно провести его и для импульсов другой формы, например пилообразного импульса. Рекомендуем читателю проделать это самостоятельно.

Спектральный анализ с прямой линейной интерполяцией функции между узлами (начало документа)

Рис. 14. 25 Спектральный анализ с прямой линейной интерполяцией функции между узлами (начало документа)

Как видно из конца этого документа (см рис 14 26), степень совпадения исходной и синтезируемой функций очень высока

Спектральный синтез на основании расчета спектра, показанного на рис. 14. 25 (конец документа)

Рис. 14. 26 Спектральный синтез на основании расчета спектра, показанного на рис. 14. 25 (конец документа)

Во всех приведенных примерах использован достаточно сложный случай. импульс с маленькой полкой на линейном росте и резким спадом В реальной ситуации функция у ft) чаще всего является довольно плавной и эффект Гиббса проявляется гораздо в меньшей мере, чем в приведенном тестовом примере. Это говорит о том, что все описанные методы имеют право на жизнь

Стандартный спектральный анализ и синтез

Рассмотрев некоторые частные аспекты спектрального анализа и синтеза, мы вплотную подошли к их классической реализации и методам ее улучшения. Прежде всего отметим, что MathCAD содержит средства, позволяющие провести спектральный анализ по классическому алгоритму, описанному в любом учебнике математики или в книгах по спектральному анализу.

К сожалению, классический метод спектрального анализа с вычислением коэффициентов Фурье численным интегрированием имеет ряд недостатков. Интегралы для коэффициентов Фурье вычисляются приближенно. Подынтегральные функции имеют быстро осциллирующие синусные и косинусные множители, что затрудняет интегрирование с малой заданной погрешностью. В итоге интегрирование идет довольно медленно, а точность вычислений оставляет желать лучшего. Эффект Гиббса не подавляется, поскольку его проявление связано с ограничением числа гармоник, которое имеет место при практической реализации данного алгоритма. Результаты анализа в значительной мере зависят от конкретной реализации интегрирования (к примеру, они различны у различных версий системы MathCAD). Время интегрирования достаточно значительное.

В основе так называемого стандартного спектрального анализа лежит вычисление интегралов, определяющих коэффициенты Фурье, простейшим численным методом прямоугольников Может показаться, что это большой шаг назад в сравнении с классическим методом. И уж тем более трудно поверить, что такой метод является единственным научно обоснованным методом вычисления этих коэффициентов [29, 30] Тем не менее это так. И понятно, почему. Если функция y (t) задана рядом дискретных отсчетов (вектор Yi), мы не имеем права предполагать, что какая-либо интерполяция значений y (t) между узлами имеет преимущество перед постоянством y (t). Строгий теоретический анализ показывает, что синтез у ft) по максимальному для данного числа отсчетов количеству гармоник при интегрировании методом прямоугольников дает наименьшую среднеквадратичную погрешность.

Документ на рис. 14. 23 показывает спектральный анализ и синтез стандартным методом (в варианте, описанном в [2]).

Стандартный спектральный анализ (начало документа)

Рис. 14. 23 Стандартный спектральный анализ (начало документа)

Результаты синтеза (см. рис 14 24) показывают, что синтезированная кривая удачно описывает быстрые детали исходной зависимости Явно видно сильное проявление эффекта Гиббса. Впрочем, нередко можно подобрать оптимальное число гармоник (или длительность отдельных участков исходной функции), при котором эффект Гиббса становится малозаметным. Однако это не более чем частный случай. Увеличение числа используемых для синтеза гармоник свыше N/2, где N— число отсчетов функции, невозможно.

К достоинствам стандартного метода относится то, что его применение значительно ускоряет спектральный анализ. Это связано с тем, что интегрирование производится по простейшим формулам без использования алгоритмов и изменяющимся в его ходе шагом.

Итак, стандартные анализ и синтез применимы для любого числа отсчетов функции, но не свободны от сильного проявления эффекта Гиббса. Известен ряд методов ослабления или подавления этого эффекта [2] Отметим лишь самый простой способ — коррекция амплитуды гармоник с помощью корректирующего множителя, постепенно ослабляющего высшие гармоники спектра.

Вид фигуры (конец документа)

Рис. 14. 6 Вид фигуры (конец документа)

Изменяя параметр К, можно получить множество других объемных фигур Функциональная окраска придает фигуре весьма реалистичный вид Этот пример наглядно показывает, что по возможностям графики система MathCAD 7 О PRO уже приближается к системе Mathematica 222, лидеру среди систем символьной математики для персональных компьютеров

Вычисление характеристик системы по ее операторной функции

Если схема описана операторной функцией, по ней можно вычислить важнейшие характеристики линейной системы. АЧХ, ФЧХ и переходную характеристику (т е. реакцию системы во времени на единичный скачок напряжения или тока на ее входе) Для вычисления АЧХ и ФЧХ достаточно заменить оператор p на величину iw, тогда модуль полученного выражения будет описывать АЧХ, а аргумент — ФЧХ

Построение АЧХ и ФЧХ для системы второго порядка, описанной операторной функцией, дано в документе на рис 14 40.