Синее и черное, или Задача Удодова

Марков снял сапоги и, вздохнув, лег на диван.

Ему хотелось спать, но, как только он закрывал глаза, желание спать моментально проходило. Марков открывал глаза и тянулся рукой за книгой. Но сон опять налетал на него, и, не дотянувшись до книги, Марков ложился и снова закрывал глаза. Но лишь только глаза закрывались, сон улетал опять, и сознание становилось таким ясным, что Марков мог в уме решать алгебраические задачи на уравнения с двумя неизвестными.

Даниил Хармс. «Сон дразнит человека»

Система алгебраических уравнений с двумя неизвестными для многих литераторов является вершиной математической премудрости. Вот еще одна цитата, дополняющая эпиграф первого этюда книги, – беседа чеховских персонажей: отставного губернского секретаря Удодова, его сына Пети и горе-репетитора Егора Зиберова, ученика VII класса гимназии:

Теперь по арифметике... Берите доску. Какая следующая задача?

Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует:

– «Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?» Повторите задачу.

Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.

– Для чего же вы это делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю!

Зиберов делит, получает 3 с остатком и быстро стирает.

«Странно... – думает он, ероша волосы и краснея. – Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая...»

Учитель глядит в ответы и видит 75 и 63.

«Гм!.. странно... Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».

– Решайте же! – говорит он Пете.

– Ну, чего думаешь? Задача-то ведь пустяковая! – говорит Удодов Пете. – Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич.

Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет.

– Это задача, собственно говоря, алгебраическая, – говорит он. – Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил... понимаете? Теперь, вот, надо вычесть... понимаете? Или, вот что... Решите мне эту задачу сами к завтраму... Подумайте...

Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол.
– И без алгебры решить можно, – говорит Удодов, протягивая руку к счетам и вздыхая. – Вот извольте видеть...


Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.
– Вот-с... по-нашему, по-неученому.
Фрагмент из миниатюры А. П. Чехова «Репетитор» предварил наш рассказ о пакете Mathcad по трем причинам:
1. Описанная ситуация часто повторяется и сейчас. Только люди, решая задачи, стали протягивать руку не к счетам и даже не к калькулятору, а к персональному компьютеру. И самая подходящая на сегодняшний день программная среда для решения задач, подобных задаче Удодова, – это Mathcad.
2. Технология решения задач в среде Mathcad во многом похожа на подход Удодова-отца. Компьютеру достаточно сообщить условия задачи – и пусть себе решает, лишь бы ответ сошелся. О методах решения задач пользователь начинает задумываться, когда происходит осечка, что случается довольно редко, если иметь в виду не слишком сложные задачи (не суперзадачи, решение которых требует разработки специального матобеспечения).
3. И современная, и прошлого века – обратитесь еще раз к рассказу А. П. Чехова – методика преподавания школьной и вузовской математики, физики, химии и других предметов ориентирована, как правило, не на постановку задачи, а на решение уже кем-то сформулированных проблем. Компьютеризация школы (средней и высшей), базирующаяся на преподавании языков программирования (BASIC, Pascal, С и др.) в качестве основ информатики, ничего не меняет в этом не совсем нормальном положении вещей. Среды общения с ЭВМ на почти естественном для человека языке (и в то же время на математическом языке), к которым относится Mathcad, позволяют больше внимания уделять постановке проблемы, математическому моделированию реальных ситуаций, анализу ответа, а не методикам решения надуманных задач. К этому вопросу мы еще вернемся в этюде 7, когда речь пойдет о методике использования компьютеров на уроках математики – школьной и вузовской.
Но лучший способ оценить пакет Mathcad – это решить с его помощью задачу. А самый подходящий пример для начального знакомства с пакетом Mathcad – чеховская задача. Вот три отрывка из рассказа, определяющие три возможных подхода к решению:
1. – И без алгебры решить можно, – говорит Удодов, протягивая руку к счетам и вздыхая. – Вот извольте видеть...
2.      Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
3.      – Это задача, собственно говоря, алгебраическая, – говорит он (Зиберов). – Ее с иксом и игреком решить можно.
Ниже читатель может увидеть эти три решения задачи о купце и сукне: Удодова-отца (рис. 1.1, 1.4 и 1.5), Петин (рис. 1.6) и Зиберовский (рис. 1.7), реализованные в среде Mathcad.

Задача о балке, или Вариации на тему русской пословицы

Лучше один раз увидеть [протокол решения задачи], чем сто раз услышать [о возможностях пакета] – следуя такому «расширению» пословицы, рассмотрим решение в среде Mathcad классической задачи теоретической механики из раздела «Статика» – задачи о равновесии балки.

Великолепная семерка Mathcad

Раз уж мы залезли в мистику (в описание магических свойств числа семь), то подошла пора рассказа о великолепной семерке

Mathcad – о семи видах графиков, используемых для визуального отображения различных зависимостей. Типов графиков в Mathcad, конечно, намного больше, но на панели инструментов имеется ровно семь кнопок для создания семи типов графиков. Мистика, да и только.

Графики очень помогают решать поставленные задачи. На рис. 1.8, например, начальные приближения к корню системы брались вблизи точек пересечения линий на графике. Глядя на выражение, можно узреть там корни, минимумы, максимумы и прочие интересные точки, только обладая сильно извращенным математикой воображением. На графике же все видно как на ладони.

К сожалению, графики, помещенные в книге, черно-белые. Их можно было бы расцветить, как это имеет место на экране дисплея, но цена книги от этого резко увеличилась бы. А ведь она адресована студентам и инженерам (см. название). Сейчас автор пишет книгу под условным названием «Mathcad для «новых» русских» с цветными иллюстрациями. Есть уже первые задачи для нее – задача о купце и сукне (см. рис. 1.14), задача о качестве менеджера (рис. 4.6 и 4.17) и задача о финансовой пирамиде (рис. 5.4) и др.

Но вернемся к графике.

Если нажать соответствующую кнопку панели инструментов (см. рис. 1.2 и 1.3), то раскроется панель графики с девятью новыми кнопками (см. рис. 1.17).

Нажимая на них, можно построить семь типов графиков. Сделаем это для иллюстрации решения задачи о балке, схема которой помещена на рис. 1.12.

На рис. 1.17-1.19 и 1.21-1.25 графически отображены реакции опор балки в зависимости от угла ее наклона при фиксированных других параметрах. Функциональные зависимости x, y и P (реакции опор – см. пункт 2 на рис. 1.17, пункт 5 на рис. 1.20, пункт 8 на рис. 1.24 и пункт 9 на рис. 1.25) взяты из главы 7, где наша система, описывающая равновесие балки, решается аналитически (см. рис. 7.9).

Операторы и функции

В математике есть основополагающее понятие – соотношение: имеется два множества; каждому элементу первого множества соотносят элемент второго множества. Частным случаем такого соотношения является функция одного аргумента – каждому значению угла (первое множество) соответствует значение, например, синуса (второе множество), косинуса и т.д. Читатель средних лет тут сразу вспомнит знаменитые таблицы Брадиса с такими «множествами» углов, синусов, логарифмов и других нужных для расчетов данных. Естественно, Mathcad не хранит множество углов и множество соответствующих им синусов, а рассчитывает эту тригонометрическую функцию по определенному алгоритму. Насколько он точен и быстр – это второй вопрос.

Можно говорить о двух множествах чисел, одном множестве функций и еще об одном множестве переменных и о множестве значений определенного интеграла: каждой четверке элементов первых четырех множеств соответствует один элемент пятого множества. Здесь речь идет об операторе определенного интеграла с четырьмя операндами, который также есть в среде Mathcad.

Лет двадцать назад наметилось некое несоответствие в трактовке терминов «функция», «оператор» математиками и программистами[24].

Математик, читая эту книгу, может сделать абсолютно законный вывод, что автор не вполне понимает, что такое оператор и что такое функция. Более того, в самом программировании нет полного единства в определении этих основополагающих понятий. То, что мы называем оператором в среде Mathcad, в среде языка BASIC называется иначе, и наоборот. Так, в среде языка BASIC есть очень удобный оператор Swap(a, b), меняющий в переменных a и b их содержимое. Этот оператор ничего не возвращает и, следовательно, с точки зрения пользователя Mathcad не может называться оператором. С другой стороны, операторы и функции Mathcad сами по себе тоже могут ничего не возвращать, а просто находиться в Mathcad-документе и ждать, когда с ними что-нибудь сделают. Например, поместят в левый операнд оператора вывода числового значения. Вот тогда-то они начнут возвращать то, что записано в приложениях 2 и 3.

Будем считать, что термины «оператор» и «функция» программно-зависимы, и рассмотрим не их суть (об этом пусть спорят теоретики), а отличия друг от друга в среде Mathcad.
Вот тест на внимательность читателя: заметил ли он разницу в использовании тригонометрических функций sin и cos на рис. 1.15 и 1.16. На первом рисунке аргумент a заключен в скобки, а на втором – нет. На рис. 1.16 можно было бы написать более экзотически (по-арабски): a sin и a cos.
Дело в том, что вычисление синуса и косинуса на рис. 1.15 ведется через вызов функции, а на рис. 1.16 – через вызов оператора. Для компьютера нет никакой разницы между функцией и оператором: и в том и в другом случае все сводится к вызову соответствующей вычислительной процедуры. Разница важна для пользователя, который еще в школе на уроках математики привык, что сложение, например, – это оператор с двумя операндами: 2 + 5, а синус – функция с одним аргументом: sin(a). Но ничто не мешает нам складывать через вызов функции (встроенной или пользовательской):
сложить(a, b):= a + b
сложить(2, 5)=7,
а рассчитывать синус и косинус через вызов оператора – см. рис. 1.16.
Функции вводятся в документ, как правило, через нажатие соответствующих кнопок: «s», «i», «n», «(» и т.д. Но лучше для этого использовать «мастер функций» (рис. 1.28).

A philosophical-religious aspect of the problem

A naturalist interested in a real-world phenomenon has no ability to appeal straight to the Creator (God or Nature, according to your choice) but has to ask the research object itself – that is, carry out an experiment by perturbing this object and investigating its reaction.

A program has its own creators, the authors. Their names are not always specified on boxes, disks and in the documentation, but they do exist. Hence – theoretically – it should be unnecessary to experiment with programs. All questions that may arise ought to be answerable either by the documentation or the authors themselves. But – in practice – if a user wishes, for instance, to identify the measurement unit (degrees or radians) of a sine function, they won't rummage in the documentation. They will simply define x:= sin(90) and observe the x variable value.

Such experiments are carried out hourly by users, who appeal to the documentation only in extremely complicated cases, as a rule when they're not satisfied with their own answer. And it's rather problematic to appeal to the creator. The program dealers, not the authors, run the support hotline; and readers well know that this isn't the same thing. The hotline operator will most likely offer to test the program and try to find out the answer, and ask you to ring back in a couple of days. And it would often be ineffective to ask the authors, who have forgotten their offspring and are entirely engrossed in a new project. Even if that isn't so, they can't be expected to remember all the properties and nuances of their creation.

That is why users usually forget that a program is a product of human intelligence and skills, supposing – at an emotional level – that it's a fruit of the efforts of an anonymous and unattainable Creator who doesn't have a support hotline. Here, most probably, lies a philosophical explanation (but by no means justification) of the widespread practice of illegal program copying. We're not talking about deliberate larceny, like creating Chinese-Bulgarian CD-ROMs labelled "Everything for your Office".[1] Here, we are dealing with relatively honest people, installing a program on their computer from the above-mentioned CD-ROM in order to understand its nature and to share their knowledge, for instance with students.

One might think that the Creator, by throwing an apple from above and hitting Newton's head, had unveiled one of the mysteries of His Divine Plan. The genius, Newton, had the advantage of finding himself in the right place at the right time.[2]
Programs are also figuratively falling at our feet from above, under circumstances when one is not obliged to pay money, crazy amounts by Russian standards, for them. Hence a shareware ethos ensues, and it is dealers who primarily resist this idea, rather than the program authors.
The saying goes that God created Man in His own image, but it could be argued that this also applies to the computer. The program code is the soul breathed into a spiritless pile of magnetic iron. For humans, body trading (transplantation of organs, transfusion or, at last, prostitution) is the reality of contemporary life; traffic in souls is a matter for fairy tales and fiction (the Faust story, for example). When we purchase software, we are getting only a "body": disks, documentation, information and discounts for the new versions, and, chiefly, the after-sale service.

Гремим пожарными ведрами

Из круглой жестянки по несложной технологии изготавливается пожарное ведро (см. пункт 1 на рис. 2.1): вырезается сектор, затем полученная выкройка сворачивается в конус (точка a подтягивается к точке c), а шов сваривается (паяется).

Задача об оптимальном плане выпуска стульев

Суть задачи. Мебельная фабрика может выпускать стулья двух типов ценою в 8 и 12 условных единиц (у.е.[15]). Под этот заказ выделены материальные и людские ресурсы. Кроме того, известно, сколько досок, ткани и времени идет на изготовление каждого стула:

Стул		Расход досок, м		Расход ткани, м2		Расход времени, чел.-час.
Первый		2		0.5		2
Второй		4		0.25		2.5
Ресурс		490		65		320

Спрашивается, как нужно спланировать производство стульев, чтобы наделать их либо количеством, либо ценой поболее. Это и отображено в отчете о решении задачи на рис. 2.9.

Задача об оптимальных перевозках

На рис. 2.10 решается одна из разновидностей задач линейного программирования – транспортная задача: необходимо ежедневно с первого склада перевозить в два магазина 50 телевизоров[16], а со второго склада – 70. При этом первый магазин продает в день 40 телевизоров, а второй – 80 (50+70-40). В транспортной задаче неравенства в ограничениях заменены равенствами. Получается система линейных алгебраических уравнений, но не с одним, как в задаче о купце и сукне (см. рис. 1.6 и рис. 1.7) или в задаче о балке (см. рис. 1.15 и рис. 1.16), а с множеством решений, одно из которых оптимизирует целевую функцию. Известны затраты на перевозку одного телевизора со складов в магазины[17]

(четыре константы: 1200 у.е. при перевозке одного телевизора с первого склада в первый магазин, 1600 – с первого склада во второй магазин, 800 – со второго склада в первый магазин и 1000 – со второго склада во второй магазин).

A cultural aspect of the problem

Open the first page of any Western publication and you will notice the prohibition on duplication, whether chapters or pages, of the book. (I originally wrote "the formidable warning will strike your eye", but in the interest of neutrality replaced it with "you will notice"). Everyone is quite aware that only commercial duplication is meant here. Both Western and Russian libraries are quite legally equipped with photocopiers, which allow a book or a magazine to be 'xeroxed' from cover to cover, except maybe the very page with the formidable, but probably futile, warning. It is possible to duplicate the printed matter in every possible way for educational and scientific purposes (to copy an extract to an exercise book, for example).

Moreover, any hindrance for this kind of information distribution is regarded as a direct infringement of the rights of the author: not of the copyrights[3] but specifically "the rights of the author". But behind this phraseology is the fact that almost without exception, it is not the author controlling the copyright, but the publisher. The authorial rights are like human ones given 'from heaven', which can't be transferred to anyone. It is the copyright owner who is disappointed by the appearance of 'black' books on the market. The author (owner of the author's rights) may be at first flattered, but then he becomes worried about the future, but as a rule ephemeral, loss of profit[4].

The vagueness of the borders between commercial and non-commercial use can be illustrated by another fact. Suppose a graduate student has Xeroxed enough articles of other authors, and has sculpted from them a dissertation (let's be more tactful – a part of the dissertation) then received a scientific degree, and afterwards, with its help, a high-paid post in a firm or university. Even if "has sculpted from them" is replaced with "has used them as research material", the essence of the matter doesn't change: the knowledge is the most precious article in the civilised market.

Computer users are among the most avid reading public nowadays: not only adverts for romantic novels are flashing by in the Metro, but also those for various User Guides or "Excel for Dummies". This applies not only to printed matter but also to software, which is a programming product (production, products and similar are all marketing expressions). Studying a program is just as interesting and useful, culturally and educationally, as studying a book. A misfortune for programs, but perhaps a hidden blessing, is their easy copying. They can be duplicated much more easily than books. Furthermore, even the most ingenious programs are obsolete before the copyright expires, in contrast to the works of classical literature. Nowadays anyone nowadays can publish the undying compositions of Pushkin and Shakespeare.

Взгляд шутника

Есть особый род шутников (к ним относит себя и автор), получающих удовольствие от попыток розыгрыша компьютера. «Много ты, машина, о себе воображаешь. Посмотрим-ка, проглотишь ли ты вот это?!», – так или примерно так думают они, вводя в ЭВМ заведомо «неправильную» информацию. Анализ реакции компьютера (программной среды) на подобные шутки пользователя может дать не меньше, чем классический разбор программы.

В этюде будет рассмотрено решение в среде Mathcad задач из области вычислительной математики. Примеры взяты не из пакета Mathcad (хотя там есть схожие задачи), а из других источников, и подобраны так, чтобы можно было показать не только легкость и изящество их решения, но и возникающие при этом осложнения и пути их преодоления. К примерам, которые прилагают к пакетам фирмы-разработчики, следует относиться с большой опаской. Тут можно вспомнить эпохальную вычислительную машину «Наири», в матобеспечении которой была программа «Поиск минимума функций». Так вот, после опробования слово функций (множественное число) в ее названии приходилось менять на слово функции (единственное число), так как минимум искался только у приложенной к программе функции и больше ни у какой другой.

Взгляд дериватора

Есть особый род извращенцев… Автору не хватило духа вынести этот термин в заголовок этюда, и он заменил его нейтральным, производным от латинского derivatio (отклонение). Читатель, может быть, до этого места книги не доберется, а об авторе подумает черт знает что. Так вот, есть особый род дериваторов, получающих удовольствие от попыток решения задач программными средствами, для этих целей прямо не предназначенными.

– А вы ноктюрн сыграть смогли бы на флейте водосточных труб?!

– А вы тра-та-та та-та-ра-та бы в среде программы тра-та-та?!

Взгляд эстета

После выстрела и команды «Искать!» собака может вернуться к охотнику с тремя результатами:

1.    Собака приносит подстреленную дичь.

2.    Собака, израсходовав отпущенный лимит времени или услышав призывный сигнал охотника, возвращается с пустыми руками, пардон, зубами.

3.    Охотник получает «трофей» – стреляный пыж или рваный башмак, но собачьи глаза и собачий хвост выдают собачью хитрость.

Есть особый род эстетов, получающих удовольствие от попыток облагораживания технического текста цитатами из художественной литературы. Но не этот смысл слова «эстет» подчеркнут в названии этюда. Автору уже не раз доводилось признаваться своим читателям, что для него в программной среде важны не только чисто технические параметры (быстродействие, богатство встроенных функций и т.д.), но и «красота» программы. Под красотой же следует понимать не только цветовую палитру или изящество окон и иконок, но и то наслаждение, которое программа может доставлять при решении даже простейших задач. И не только своими новыми, ранее неведомыми возможностями, но и своими... ошибками. Автор попытался было описать всю эту гамму чувств, но его опередил Карел Чапек своим рассказом «Игла», где необыкновенно точно передан дух расчетов – и не важно, проводятся ли они на бумаге или на компьютере. Помимо этого, чапековский отрывок поможет понять, при чем тут охотник:

Когда я работал в бухгалтерии и составлял, бывало, полугодовой отчет, подчас случалось, что цифры не сходятся. Однажды в наличности не хватило трех геллеров. Конечно, я мог просто положить в кассу эти три геллера, но это была бы неправильная игра. С бухгалтерской точки зрения это было бы неспортивно. Надо найти, в каком счете допущена ошибка, а счетов у нас было четырнадцать тысяч. И скажу вам, когда я брался за баланс, мне всегда хотелось, чтобы там обнаружилась какая-нибудь ошибка. Тогда я, бывало, оставался на службе хоть на всю ночь. Положу перед собой кучу бухгалтерских книг и берусь за дело. И для меня колонки цифр становились не цифрами, они преображались просто необыкновенно. То мне казалось, что я карабкаюсь по этим колонкам вверх, словно на крутую скалу, то я спускаюсь по ним, как по лестнице[35], в глубокую шахту. Иногда я чувствовал себя охотником, который продирается сквозь чащу цифр, чтобы изловить пугливого и редкого зверя – эти самые три геллера. И до того мне в такие минуты становилось хорошо от этого ощущения движения и силы, такое я чувствовал вокруг себя волнующее приволье, словно и в самом деле переживал необыкновенное приключение. Целыми ночами я мог охотиться за тремя геллерами, и когда находил их, то даже не думал, что это лишь жалкие гроши. Это была добыча, и я шел спать, торжествующий и счастливый...

Поиск решения с помощью функций root, Find, MinErr, Minimize и Maximize во многом напоминает ружейную охоту. Пользователь формирует анализируемую функцию, вводит ограничения, выставляет параметры поиска (заряжает ружье, выслеживает дичь), а затем нажимает клавишу F9 (спусковой крючок ружья). Собака (cреда Mathcad) прыгает в воду и возвращается с тремя результатами:
1.    Решение найдено (см. пункт 4 рис. 3.1).
2.    Решение не найдено (пункт 5).
3.    Mathcad пытается подсунуть пользователю то, что только издали напоминает правильный результат (пункт 6).
При этом ситуация осложняется еще и тем, что пользователь Mathcad, в отличие от охотника, который знает, что такое дичь, часто не имеет понятия о том, что такое правильный результат. У среды Mathcad, к сожалению, нет глаз и хвоста, по которым можно определить, что именно принесено к ногам охотника – пользователя пакета.
Работа с функциями root, Find, MinErr, Minimize и Maximize – это хождение на охоту с чужой собакой, повадки которой неизвестны. «Своя собака» – это методы и алгоритмы, написанные на языке Mathcad и вставленные в документ, по которым решение ищется не вслепую, а наверняка (см. этюд 6). А если писать программы недосуг, то вот семь советов по работе с функциями root, Find, MinErr, Minimize и Maximize:
1.    Найдя решение, еще раз заставьте Mathcad найти его уже от новой опорной точки. Неплохо при этом использовать одновременно все инструменты, заложенные в Mathcad. Из этюдов 2 и 3 мы знаем, что максимум, например, можно искать минимум тремя способами (нечаянный каламбур!): через поиск корней системы уравнений, составленных из частных производных анализируемой функции, с помощью функции MinErr и прямым способом – через функцию Maximize. Что здесь сработает – неизвестно, наверное, даже разработчикам Mathcad. Если из разных опорных точек разными методами найден один и тот же результат, то надо перекреститься и сказать: «Слава Богу! Задача решена!»


2.    Перед решением оптимизационной задачи с ограничениями прогоните ее не с функцией MinErr, Minimize или Maximize, а с функцией Find для того, чтобы оценить область существования решений.
3.    Начинайте поиск оптимального решения от одной из точек, найденных в пункте 2 и лежащих недалеко от оптимума.
4.    Вводите ограничения постепенно: ввели первое – нашли какое-то подобие решения, ввели второе – уточнили его и т.д.
5.    Начинайте решение оптимизационной задачи с целочисленными аргументами без ограничений на целочисленность. Нецелочисленный ответ всегда будет полезен, так как 1) от него можно начать поиск целочисленного решения, 2) можно удовлетвориться нецелочисленным решением (появление совместителя, например, в задаче об оптимальном штатном расписании) и 3) числа можно округлить вручную, если целочисленное решение отыскать невозможно.
6.    Проверяйте правильность найденных корней, минимумов и максимумов построением графиков и поверхностей, где эти точки видны, благо пакет Mathcad имеет богатый набор графики. Если аргументов у функции больше двух, постройте графики сечений через точку оптимума (рис. 3.5) по всем координатам и убедитесь, что там все частные производные равны нулю. Неплохо тут протабулировать анализируемую функцию вокруг найденной точки и показать, что отход от оптимума ухудшает результат.
7.    Прежде чем решать задачу численно, проанализируйте ее средствами символьной математики (этюд 7). Если даже аналитическое решение не будет найдено, то можно, например, выведенную частную производную использовать в численном решении системы (гибридность решения задачи – см. раздел 7.5).
[1] Он уже был раскрыт в двух предыдущих изданиях книги. Автор еще раз просит у читателя прощения за повторы и за самокомпиляцию (см. также предисловие).
[2] Рутинные операторы, формирующие матрицу M, по которой строятся графики, захлопнуты – см. рис. 2.7, где они открыты.


[3] Это и понятно: поиск корней уравнений – задача нередко существенно более сложная, чем задача поиска минимума. Поэтому чаще поступают наоборот: для решения системы уравнений составляют выражение (функционал), частные производные которого – это выражения исходной системы. У функционала ищут минимум, который одновременно является и корнем исходной системы.
[4] В среде Mathcad есть много других функций, генерирующих случайные числа с иными законами распределения.
[5] Это мы считаем, что fuzzy переводится как «пушистый», но это еще и «not in focus», то есть «нечеткий».
[6] Если, конечно, точно вычисляется значение p в пределах первых 15 цифр.
[7] Продолжим мысль А.С.Пушкина и воскликнем: «Каким образом программист в ограниченном наборе функций и команд видит будущую Программу?»
[8] Горе от ума, точнее, от высоких технологий – от цифрового, а не аналогового способа отображения реальности.
[9] В Mathcad-документе на рис. 2.2 эти вектора также формировались при построении графика. Так что перебор присутствовал и там, но был завуалирован.
[10] Здесь мы от текстового индекса отказались, чтобы читатель не путал его с числовым индексом и чтобы не получались трехэтажные индексы.
[11] Слово «враждебное» здесь не совсем точно передает суть проблемы, но читатель понимает, о чем идет речь. Так учитель подсовывает ученику заковыристый интеграл, любя его (и интеграл и ученика) и понимая, что с подобным интегралом ученик, слава Богу, никогда не столкнется, решая реальную задачу.
[12] Проблеме качественной подготовки персонала в энергетике стали уделять особое внимание после Чернобыльской катастрофы.
[13] Известный русский адвокат Лохвицкий (отец писательницы Тэффи) помог советом одной даме выпутаться из весьма затруднительных обстоятельств.
– Не знаю, как Вас благодарить! – воскликнула эта дама, встретив адвоката через некоторое время.
– Сударыня, – сказал Лохвицкий, – с тех пор, как финикийцы изобрели деньги, этот вопрос отпал сам собой.
[14] Бартер покоится на трех китах: а) неумение производственников работать в новых условиях, б) желание


уйти от налогов и в) процветание
фирм-паразитов (посредников), имеющих на реализации бартерных операций существенный «навар». Кроме того, денежный обмен убивает инфляция. В товарной цепочке все дорожает более-менее одинаково.
[15] Белая эмаль ПФ-115, если это кого-то интересует.
[16] Без этого, на первый взгляд лишнего ограничения могут получиться довольно казусные решения типа «купи на стороне маленькие банки с краской, сдай их на завод, а вместо них получи дополнительные большие – лимит отпущенных денег не будет превышен, но объем краски увеличится».
[17] Мне всегда в таких ситуациях вспоминается строка Франсуа Вийона: «От жажды умираю над ручьем...»
[18] Новая оптимизационная задача линейного программирования, которая передо мной, слава Богу (или увы – новый этюд в книгу), не стояла: Котовская ТЭЦ выделила пятитонный ЗИЛ.
[19] Исключение из правил – учебный процесс: вспомним суворовское «Тяжело в ученье – легко в бою».
[20] 16×63 = 1008, но счет барабанов у нас начинается не с единиц, а с нулей. Числа 16 и 63 легко найти на калькуляторе, разделив 14 миллионов на стоимость литра краски, перемноженной на емкость барабана – 55 и 15 литров.
[21] Автор в свою очередь немножко обманывает читателя: не присочинишь, не напишешь книгу. На самом деле все оказалось проще, а Оля по-своему была умнее всех нас: она отнесла 186 тысяч в графу «Коммерческие услуги» – и никакой оптимизации.
[22] Такой вариант расфасовки (чертова дюжина в квадрате) страшновато было везти из Котовска в Москву.
[23] Две целевые функции (объем и стоимость) в задаче о краске можно объединить в одну, перемножив или сложив их.
[24] Ломает линейность задачи такой распространенный прием, как скидка оптовикам – цена единицы товара падает при увеличении объема его закупки.
[25] Эта главка написана совместно с В.Усенко.
[26] Здесь спокойно можно обойтись без if: с логическим умножением все ясно; логическое сложение будет давать либо нуль, либо число, отличное от нуля.
[27] Текстовый процессор Word, в среде которого писалась книга, заметил ошибку в этом предложении и, либеральничая, выдал сообщение: «возможно, не хватает запятой после слова «нельзя».
[28] В среде Mathcad 8 все переменные имеют тип Variant (стандарт технологии OLE 2).
[29] Вариант названия этой главки книги: «Mathcad и «цветная» булева алгебра».
[30] Терпимость, отказ от крайних оценок и суждений.
[31] Их раскаты продолжают звучать в Северной Ирландии, на Балканах, на Кавказе, заглушая истинные причины конфликтов (см. дивертисмент № 1).
[32] Комплексная переменная позволяет перевести вопрос с отрезка на прямой (дилемма: виновен – невиновен) на плоскость (трилемма: виновен – невиновен – а было ли вообще преступление).
[33] Писатель с трагической судьбой, умевший как никто другой облекать самые глубокие мысли в самые «нелепые» литературные формы.
[34] Оружие делает равными хлипкого интеллигента, кующего славу и богатство Родины, и «качка», делающего страну пугалом для всего цивилизованного мира.
[35] См. рис. 2.6 в этюде 2– прим. автора.

A police aspect of the problem

There are always articles in the Russian press about the routine dispersal of pirate CD-ROMs of popular computer programs, by traders in Moscow outside the OMON (civilian police headquarters); somewhere at the All-Russian Exhibition Centre (formerly the NKVD building); in the Mitino district; and near the Gorbunov Palace of Culture (a favourite location called "Gorbushka").

One's first reaction is: "At last!" But later, other ideas surface. When people with machine guns at the ready are examining a hawker's documents in a pedestrian subway, nine out of ten passers-by assume not that they're enforcing law and order, but collecting a cut to turn a blind eye. The tenth passer-by believes that the small fry will be hauled in again, while the real organisers of illegal trade will get off with a mild scare. God forbid the idea that any problem can be solved purely by police action in our country! It has not proved a workable approach so far, and even when it appeared so, historically it led us down the path of the Gulag labour camps. Furthermore, the possibility is always looming.

Заяц

Чтобы приготовить рагу из зайца, нужно иметь как минимум зайца. Чтобы обработать (сгладить, аппроксимировать, интерполировать, экстраполировать и т.д.) экспериментальные данные, нужно иметь как минимум эти данные.

Чаще всего экспериментальные данные представляют собой набор пар чисел (Xi, Yi), где Yi – экспериментальные значения некоторой искомой функции, а Xi – значения аргумента.

Сортировка

Пары экспериментальных данных перед дальнейшей обработкой желательно отсортировать по возрастанию значений X. Это можно сделать вручную, переставив местами две первых пары, как в нашем случае (пункт 1 рис. 4.1), или (при объемных массивах данных) автоматически через функцию csort (пункт 2 рис. 4.2), возвращающую упорядоченную матрицу по отмеченному номеру столбца (у нас это нуль[4]

– второй аргумент функции csort). Для этого оба вектора-столбца X и Y сливаются в матрицу M с двумя столбцами, которая после сортировки расчленяется на те же, но уже упорядоченные векторы-столбцы. Это приходится делать из-за того, что некоторые функции Mathcad (например, linfit, о которой речь пойдет ниже) отказываются иметь дело с неотсортированным вектором. Да и вообще, как говорят немцы, Die Ordnung muß sein! – Должен быть порядок!

Поп-стат, или Линейная интерполяция

Встроенные функции intercept (to intercept по-английски – отложить отрезок на линии) и slope (наклон) решают самую простую и самую распространенную задачу линейного сглаживания[5]

экспериментальных данных методом

наименьших квадратов (см. пункт 3.1).

Полином

Исследователю, обрабатывающему на компьютере свои экспериментальные точки, нет дела до всех этих методологических тонкостей. Не напороться бы на фактическую ошибку, и на том спасибо. Уже упоминавшийся KISS – принцип программирования призывает пользователя прибегать к закрытым алгоритмам только в крайних случаях. При поиске сглаживающего полинома Р-й степени при Р, равном единице (линейная задача), можно обойтись без функций intercept и slope, вспомнив, что эта оптимизационная задача сводится к решению системы двух линейных алгебраических уравнений. Полином более высокой степени потребует решения более объемной, но все той же линейной системы.

Полусвобода

Потребность в замене сомножителей Xk полинома более сложными формулами вызвала к жизни функцию linfit (LINear FITting – линейное сглаживание).

Опять полусвобода

При обработке данных эксперимента, разбросанных «как попало», часто хочется плюнуть на критерии оптимизации и просто провести линию (кривую или, на худой конец, ломаную, состоящую из прямых отрезков) непосредственно через точки. Благо в среде Mathcad есть для этого инструментарий: средства линейной интерполяции (функция linterp – рис. 4.7) и интерполяции сплайном (interp – рис. 4.8) – линейным (lspline), параболическим (pspline) и кубическим (cspline).

Еще немного статистики

На рис. 4.10 показано, как функция lspline может сгладить уже не линией, а поверхностью

экспериментальные точки двухфакторного эксперимента с помощью двухмерной сплайн-интерполяции. У нас есть уже не вектор, а матрица M экспериментальных точек, зависящих от двух переменных эксперимента: давления пара и его температуры.

Экспертная оценка качества чего-либо[14]

Качество есть качество. Качество нельзя измерить[15], но можно оценить. Существуют две формы оценки качества: лингвистическая и количественная. В первом случае качество определяют словами: например, «качество высокое», «среднее», «низкое» и т.д. Во втором случае качество оценивают по некоторой условной шкале числом K (0 ? K ? M, где M - высший балл в числовой оценке качества). Например, «пять», как в российской, или 100 как в английской школах.

Для оценки качества привлекаются эксперты. Экспертной оценке качества могут быть подвергнуты товары и услуги, проекты и законы, знания и квалификация, выступления фигуристов, гимнастов или вокалистов и многое другое.

В повседневной жизни при принятии решения можно исходить из лингвистической оценки качества: мы покупаем хороший чай или инструмент высокого качества

(если позволяют средства). Однако есть такие задачи, в решении которых лучше руководствоваться количественной оценкой качества. Кроме того, обычно лингвистические оценки строятся на основе экспертных количественных оценок. Так, качество выпускника английского университета и достоинство диплома, который он получает, определяется по следующей шкале:

Средний балл в интервале оценок по 100-бальной шкале		Достоинство диплома (лингвистическая оценка)
90 - 100		С отличием
85 - 90		Первой ступени А
80 - 85		Первой ступени Б
70 - 80		Второй ступени
менее 70		Обычный

Независимо от объекта, качество которого подлежит экспертной оценке, методика ее получения в основе своей одинакова.

Рассмотрим задачу оценки деловых качеств руководителя (менеджера). Для оценки потребуются модель качества менеджера, эксперты и математическая обработка результатов работы экспертов.

Модель качества специалиста может быть представлена в виде некоторого набора важнейших качественных параметров (качеств), характеризующих его профессиональный уровень, личностные, деловые качества и предопределяющих успешную работу в рассматриваемой сфере деятельности.

Допустим, что этот набор включает следующие качества:
1) уровень и качество образования, опыт практической работы,
2) эрудиция, знания и умения в своей и смежных сферах деятельности,
3) обучаемость и способность обучать,
4) культурный уровень, моральные стандарты,
5) физическое и психологическое здоровье, возраст,
6) характер, отношение к окружающим,
7) умение руководить,
8) амбициозность, стремление к лидерству,
9) способность к риску,
10) динамизм (способность оценивать и принимать изменения внутренней и    внешней среды).
Эксперты располагают данными (анкеты, опросные листы, результаты тестов и прочее), позволяющими оценить по пятибалльной системе степень принадлежности качества кандидату. Пятибалльная система привычна и обеспечивает возможность представительной оценки степени принадлежности качества кандидату, например, по следующему алгоритму:

Принадлежность качества кандидату	Оценка в баллах
отсутствует	1
проявляется в слабой степени	2
проявляется	3
проявляется явно	4
присуще в полной мере	5

Результатом работы экспертов станет таблица оценок каждого из десяти качеств модели каждым экспертом[16]
(количество экспертов определяется важностью решения и средствами, выделенными  на экспертизу).

A moral aspect of the problem

Police raids on the black-market software dealers – and this was mentioned in the mass media – were initiated by Russian computer companies, who had noticed illegal copies of their software on hawkers' stands. It's worth noting that the office workers of these companies have cut their teeth professionally on pirate copies of others' programs. They have, of course, been installing these illegal programs with the aim of general education and science, but consider the following. It's alleged that the Moscow department of a certain renowned computer company was behind the police raids. A department of that very company followed up with a lengthy series of copyright infringement trials. This renowned company would be advised to understand the Windows interface copyright before going off to inform on someone else. Have you ever seen the principal of this firm? Does he look like a man who has been robbed?

The Biblical story tells that Jesus Christ rescued an unfaithful wife from mob law, having appealed for someone without sin to cast the first stone at the miserable woman. I have a similar feeling, that our press (the voice of the crowd) attempts to invoke mob law against our miserable domestic program users[5]. In doing so, a hawker from Gorbushka and a high school teacher are quite often lumped into the same category.[6] Yes, they both indeed have illegal copies in their hands, but they should be named and, especially, judged in a different manner, considering all the above angles. The Gorbushka traders are not concerned with copyright law at all. They should be prosecuted under quite different measures and articles of law – such as infringement of trade regulations, or even larceny and robbery. The Russian software manufacturers – and not only Russian – have got into a vicious circle. On the one hand, it's valid to protect your own rights by all possible means, but on the other, you can scarcely claim the moral high ground if you have repeatedly infringed someone else's rights and will continue to do so (if your son, for instance, 'skims' virtual games from black-market disks at home).

If the program is stolen ... No, we won't hurl a stone; we'll rephrase. If the author or the copyright owner is ignorant of the program duplication, it is not a cause for concern: conversely, it should be a matter for pride that it is used (for the author, of course, rather than the dealer). The program ought to be protected by active positive means (good after-sale service[7], or an electronic key as a last resort) rather than fiscal. There's an analogy to adultery, which is piracy in family life[8]. If a man has a pretty wife, and his neighbour is leering (or worse) at her, it is wise for him to struggle against infidelities actively by gifts and declarations – in short, good after-marriage service (we can consider the ancient chastity belt analogous to the electronic key[9]). What's unhelpful is shadowing her by private detective. And it's extremely repugnant to try to enforce community fidelity by condemning other people's wives or trying to bind behaviour by Zalesskian[10] legal declarations and clauses.
It appears the author has found for himself one solution to the computer piracy problem. It's impossible to be, as the old joke goes, "a little bit pregnant". But, probably, it's possible to be "a little bit honest" in the commercial use of others' programs. My colleagues and I design programs for power stations. This work began, naturally, with illegal use of such programs as Turbo Pascal, Visual Basic etc. But as soon as we had received the first money for our own programs we sold, we didn't pay anyone's salary or buy a new computer: we had spent it on acquiring legally the software tools we had used, even if we didn't use them any more[11]. At present all our commercial projects are based on the legal programs, while the educational ones – I work in the Moscow Power Engineering Institute – for the time being aren't. More correctly, they aren't entirely: the software is bought (though not always – a stone can be hurled at us for that) for one computer, but afterwards installed on all the equipment in an educational class[12]. But the solution of this problem is only a matter of time. Russia will either finally get bogged down in different crises, or will adjust to a normal educational system (and public health service, social maintenance etc.) with appropriate financing. For the present, it would be pragmatic not to place a moratorium on the use of illegal copies, nor condemn those who apply them to general education and school aims (considering that the range of commercial use of others' programs is very wide). At one end of the scale is the post-graduate student processing experimental data, and at the other the supplier and distributor of black-market laser disks. It's hardly the nastiest of black-market dealings: let's be pleased that the trade is in hardware and programs, rather than firearms and drugs.


Chekhov, by his own confession, " squeezed out the serf from himself drop by drop". But he never had it in mind to forcibly squeeze the bad qualities from his readers. Chekhov just helped them become better through his works, and nothing more. Let's squeeze computer piracy from ourselves, drop by drop. This process should go on without hysterics, without police swoops and especially without informing, while remaining comfortable with our own conscience and casting only occasional glances at our purses and the Criminal Code.
I fear that the computer piracy problem in our country will be settled in a purely Soviet manner: through the further expansion of the administrative machinery. A computer police would be established, for instance, which in much the same manner as the tax police wouldn't be able to poke its nose into the opulent private residences, springing up all over near Moscow without any tax returns; or into the wholesale markets that service half of Moscow without any cash registers. Harassing the ordinary business person or worker, hardly surviving in our tax disorder, is what this police would do. The tax police should break in not only bootleggers' doors, but also the luxurious office of the authority, decorated on budget means (in the first case an armoured vest should be put on; in the second, napkins). So, I am afraid that the computer police, if it is nevertheless established, won't go first to Gorbushka, but to any high school or a research institute in order to impose a fine on the above-mentioned post-graduate student.
I will spend a part of royalties for this book on a legal version of the text editor which has helped it to be written. But I want to be completely frank with the reader and say that I will only do this: if royalties suffice; if no new version of the text editor appears (in which case the new one will be purchased – or "stolen"); and if I don't change my mind.
[1] As this book was being perfected, there appeared on sale a 'black' laser disk "Mathcad 8 Pro with Russian language specification". But it was a double trick: a) the disk, naturally, contained a stolen copy of Mathcad; and b) the specification turned out to be scanned or stolen from the published paperback of VP Diakonov's Mathcad 7 manual.


1 [2]There's a saying that the piano is very easily played: all you do is push the right keys at the right time! We have already emphasised this in Etude 3, discussing computer arts. And there are only a few geniuses at the piano, because the Creator is unable to attend to all players. We won't consider here the diligence of the musician (or programmer), and refer the reader to Pushkin's "Mozart and Salieri", which develops this subject rather profoundly.
[3] In English, there is no confusion between "rights of the author" and "copyright" – a right to copy. But in Russian, "copyright" is translated ambiguously as "authorial rights".
[4] Not losses but profits may arise here. An author, having written a new work, can often make much more profit if his illegal copies are no less famous than legal ones. Examples are Bulgakov, Vysotsky, Pasternak, and Brodsky; the latter two would scarcely have obtained a Nobel Prize if they had been widely published in due time.
[5] You can bet your life that those writing accusatory articles have at least one illegal program (DOS or Windows Word, or DOS Lexicon) installed on their computer. Many police departments are equipped with computers (documentation, databases and such like) but again anything may be staked that no department, including that organising the computer market raids, cares always to purchase the legal program versions. Police officials often give crime reports on television. Next to the spokesperson, as a rule, there's a computer: they're not fools. The screen shows the two blue logos of Norton Commander - stolen, by the way.
[6] There's a poster hanging in the Белый Ветер (Byeliya Vyetyer, meaning "White Wind") computer store on Nikolskaya Street in Moscow: a tattooed hand covering a mouse, with the caption above: "Don't steal!". I have walked through the store observing the prices of notebooks, the shop's speciality. If the mark-up accounts for 20-30%, it's called commercial; if 200-300%, gangsterism. The price of the most expensive Western notebook amounts to $2500 dollars. Only a special order for mother-of-pearl keys may cost more. To afford a 5000 "bucks" notebook and its entire software is only within the grasp of the very hand drawn on the poster, whose significance is somewhat different after a trip around the store.


[7] The above- mentioned Moscow department of the renowned company on the one hand is struggling with piracy, and on the other, indirectly promoting it. A certain colleague of the author bought there, for a firm he 'moonlights' for, a legal copy of the office system for $2500, though it costs 90 roubles on a hawker's stand. During the installation, advice was needed. He phoned the dealer, who replied that the after-sales service had been reassigned to another firm. He phoned there, where they said that consultations were chargeable: $60 a question. For such money they, of course, are consulting everybody, not only legal users.
[8] A sexual angle on the problem, if you like.
[9] An analogy here is in that two parties are involved: a wife and a husband (a program and a user). And the real pirates do not care a straw: it's quite easy to break both a chastity belt and an electronic key. There is another parallel: promiscuous sex and illegal program duplication are the main ways for viruses, human and computer respectively, to proliferate.
[10]Pereslavl-Zalessky is a university city in the Rostov area, home of the Program Systems Institute, where a group of programmers wrote a declaration not to use unlicensed programs.
[11] See the chapter "How the author sold programs" in Etude 3.
[12] I became acquainted with this approach while studying (good and bad) in Germany. Quite often only one program is installed on many computers there, but at the same time they ask the permission of the manufacturing firm. The firm gives permission, sufficient for the university's needs (would they find another place so suitable for the successful advertising of its products?) realising that if it refuses, the program will be installed anyway.

Эпидемия

Одно из основных потребительских качеств компьютера – это отношение цены к производительности. С подобным критерием можно подойти и к примерам, входящим в пакеты программ. Только вместо производительности нужно рассматривать занимательность задачи, а вместо цены – размер соответствующего файла. В этом смысле рекордсмен пакета Mathcad– задача «Эпидемия». Ее уникальность еще и в том, что она – единственная, автор которой (John Truxal) отмечен в разделе Acknowledgments документации пакета Mathcad.

Суть задачи. В городе, население которого составляет 20 000 человек (см. пункт 1 на рис. 5.1), появляются 50 инфекционных больных, что вызывает эпидемию. Предположим, что прирост больных за день пропорционален произведению числа здоровых (еще не переболевших и не приобретших иммунитет) на число больных. Коэффициент пропорциональности Пр интегрирует разного рода меры профилактики. Если, к примеру, жители города будут носить марлевые повязки или сделают прививки, то этот коэффициент уменьшится. Спрашивается, как развивается эпидемия: как изо дня в день меняется число больных.

Диффуры

Описанная задача об эпидемии сводится к решению задачи Коши для системы двух обыкновенных дифференциальных уравнений (ОДУ) первого порядка относительно двух неизвестных функций Больные(t) и Здоровые(t).

Больные’(t) = Больные(t) × (Пр × Здоровые(t)-1)

Здоровые(t) = -Пр × Больные(t) × Здоровые(t)

В пункте 2 на рис. 5.1, по сути, реализован метод Эйлера[3] с единичным шагом интегрирования Dt.

Больные(t+1)

= Больныеt + Dt × Больные¢t

Здоровые(t+1)

= Здоровыеt + Dt × Здоровые¢t

Заглядывая вперед, в этюд 6 (вернее, готовя читателя к нему), покажем, как вектор-выражение пункта 2 на рис. 5.1 реализуется средствами программирования (цикл с параметром):

for t Î 1..13

Больныеt+1 ¬ Пр×Здоровыеt ×Больныеt
3доровыеt+1 ¬ 3доровыеt - Пр×Здоровыеt ×Больныеt

В среде Mathcad до версий PLUS 5.0 дифференциальные уравнения без особых ухищрений можно было решать только методом Эйлера, который имеет низкую точность и производительность (плата за простоту). Инструментарий для решения дифференциальных уравнений (систем) различного порядка и различными методами появился в арсенале Mathcad PLUS 6.0. В него входят 13 встроенных функций (Bustoer, bustoer, bvalfit, multigird, relax, Rkadapt, rkadapt, rkfixed, sbval, Stiffb, stiffb, Stiffr и stiffr), работа одной из которых (rkfixed – метод Рунге ¾ Кутты (rk) четвертого порядка с фиксированным (fixed) шагом интегрирования) показана на рис. 5.2. У этой функции пять аргументов: вектор начальных значений искомых решений, абсцисса начальной точки интегрирования, абсцисса конечной точки интегрирования, число шагов интегрирования и функция-вектор правых частей системы. Функция rkfixed возвращает в матрицу (у нас она имеет имя Z) с P+1 столбцами и n строками (P – количество уравнений или порядок уравнения) таблицу решений системы: первый (вернее, нулевой) столбец – это значения аргумента t (их задает пользователь через величины tнач, tкон[4] и n), а последующие столбцы – значения ординат решения.

Еще одна «эпидемия»

А теперь наши читатели получат домашнее задание.

Даны математическая модель развития финансовой пирамиды и ее реализация по разностной схеме. Необходимо составить и решить систему дифференциальных уравнений, описывающих развитие эпидемии, пардон, финансовой пирамиды.

К задачам, решаемым на персональном компьютере, не в последнюю очередь относятся и финансовые, связанные с ведением бюджета семьи, фирмы, завода и т.д. Итак, финансы. Компьютер может помочь учитывать, сохранять и приумножать их минимум тремя способами:

1.     На компьютере заводится электронная версия бухгалтерской книги, куда записываются все доходы и расходы. Для этих целей годятся такие программы, как Excel, Lotus 1-2-3, QuattroPro (электронные таблицы), 1C:Бухгалтерия (специализированные пакеты[9]) и т.д. Пакет Mathcad, кстати, ведет свою родословную от электронных таблиц, которые также можно считать «волшебной» счетной доской. Первое его отличие состоит в том, что в среде электронных таблиц знак «равно» ставится перед выражением, а в среде Mathcad – после. Второе отличие в том, что Mathcad поддерживает графический режим интерфейса: = 5×25 + 3Ù12 (Excel); 5×25 + 312 = (Mathcad). Третье отличие, максимально приближающее стиль Mathcad к стилю написания формул на обычном листе бумаги, заключается в том, что формулы и константы электронных таблиц жестко привязаны к сетке столбцов и строк. Об этом мы подробно поговорим в приложении 7, когда будем описывать методику совместной работы Mathcad и Excel.

2.     Компьютер подсоединяется к банковской электронной сети так, что домашняя хозяйка или бухгалтер фирмы могут сами проводить необходимые платежи, не выходя из дома. Здесь на первый план выступает проблема безопасности: платежное поручение должно быть зашифровано и сопровождаться электронной подписью. Об этом мы еще поговорим в этюде 7.

3.     На компьютере можно смоделировать и просчитать ту или иную финансовую операцию (покупка облигаций или акций, открытие счета или взятие кредита в банке и т. д.) и посмотреть, во что это выльется.

Среди примеров, входящих в пакет электронных таблиц Excel, есть задача, связанная с покупкой ценных бумаг. Рассчитывается, сколько и каких акций нужно купить, имея в запасе ограниченное количество свободных денег, чтобы сумма будущих дивидендов была максимальной (задача линейного программирования – см. рис. 2.9 и 2.10 в этюде 2, 3.10 и 3.11 в этюде 3).
Среди примеров, входящих в пакет математической программы Mathcad, есть задача, связанная с моделированием развития эпидемии. Задается начальное число здоровых и больных, а далее просчитывается, как развивается эпидемия – как меняется число больных по дням. Мы только что эту задачу разобрали.
Попробуем скрестить эти две задачи и получить новую, связанную с моделированием развития финансовой пирамиды, которая во многом похожа на эпидемию. Сделаем мы это в среде пакета Mathcad, который вполне подходит для таких целей. Более того, к пакету Mathcad можно прикупить электронный учебник «Personal Finance», который поможет научиться вести финансы и из которого при необходимости в рабочий документ переносятся нужные формулы и константы.
Автор имел опыт участия в финансовых пирамидах. Первый опыт ¾ очень давний, очень невинный и без особых последствий. В школьные годы кем-то в классе было предложено не тратить выдаваемые родителями ежедневные обеденные 20 копеек, а складывать их и отдавать все разом поочередно каждому участнику этой финансовой кампании. Так воплощалась старая, как мир, детская мечта: «Вот если бы каждый взрослый дал мне по копеечке... Он бы этого и не заметил, а у меня бы оказался целый капитал». Но в классе вышло так, что участники этой складчины, получившие деньги, из игры выбывали, она потихоньку глохла и кто-то (а среди них оказался и автор) остался с носом.
Второй опыт участия в финансовых пирамидах автор приобрел вместе со всей страной 17 августа 1998 года.
Сейчас, слыша о крахе «Тибетов», «Светлан» и прочих «Чар», автор вспоминает детскую мечту, школьные двугривенные и не только их.
Банковская система любой страны, как на трех китах, покоится на трех числах. Первое число N1 – плата за кредит. Взял в банке сто рублей – будь любезен в конце года верни 100 + N1 рублей. Второе число N2 – процент по вкладу. Положил в банк сто рублей – получи в конце года 100 + N2 рублей. Разница между первым и вторым числами (N1 > N2) заставляет банки прибыльно работать. Третье число N3, подпирающее снизу два первых и заставляющее людей нести деньги в банк, – это величина инфляции[10]. В нормальной экономической ситуации низкий уровень инфляции и не очень высокая плата за кредит держат в узких рамках процент по вкладу:
N1 > N2 > N3.
Если же инфляция составляет 1000 и более процентов в год, то многие люди, забывая о ненормальности такой ситуации, легко верят в 1000 и более процентов годовых по вкладу (ведь величина N2 должна быть больше величины N3) и «ложатся в основание» очередной финансовой пирамиды. Если, конечно, законодательством страны позволительно такие пирамиды строить. Есть и менее наивные люди, понимающие, что пирамида – это особый род игры, где нужно уметь «вовремя смыться».
Итак, строим финансовую пирамиду.

Немного истории

При работе в среде Mathcad всегда ощущалась потребность в программировании для расширения и совершенствования базового набора математических инструментов – операторов и функций. Искушенные пользователи решали эту проблему тремя путями.

Путь 1. В самых первых версиях Mathcad были[2] две функции (if и until), позволявшие через различные хитрости и трюки реализовывать две основные алгоритмические конструкции – выбор (if) и повторение (until). Хитрить же приходилось из-за неспособности функций if и until иметь в качестве аргументов блок составных операторов. Поэтому для реализации даже несложного алгоритма нужно было подключать механизм вложенных функций и

операторов, что нередко превращало программу

в настоящую криптограмму, в которой даже сам автор разбирался с трудом.

Вот как выглядит поиск корня уравнения методом половинного деления (рис. 6.1) с использованием функции if и until (автор А.Шевченко). Читатель, забегая вперед, может сравнить «программу» на рис. 6.1 с программой (без кавычек) на рис. 6.20, реализующей практически тот же алгоритм.

Панель программирования

С первого взгляда на Mathcad возникает вопрос: почему в него не был встроен какой-либо известный и широко используемый язык программирования, а разработан новый, ни на что не похожий[4]? Электронные таблицы Excel, текстовый редактор Word и базы данных Access (Microsoft Office) используют встроенный BASIC[5], что кажется естественным даже для самых непримиримых противников этого языка. Но после детального знакомства с языком Mathcad удивление сменяется пониманием и даже удовлетворением. Становится очевидным, что в рамки традиционных языков с их программами в текстовом формате невозможно втиснуть богатый набор инструментария Mathcad, который реализован не только и не столько в виде функций, сколько в общепринятом в математике виде[6].

В Mathcad, по сути, не встроен язык программирования, а просто снято вышеупомянутое ограничение на использование составных операторов в теле алгоритмических управляющих конструкций выбора (if) и повторения (until).

Кроме того, введено понятие локальной

переменной, добавлен цикл с параметром for, операторы досрочного выхода из цикла break и continue, а также оператор досрочного выхода из программы return. Алгоритмические конструкции в среде Mathcad вводятся не традиционным набором через клавиатуру ключевых слов if, then, else, while и т.д., а нажатием одной из кнопок панели программирования (Programming):

Программа-константа – программа-переменная – программа-функция

Кнопки программирования (см. рис. 6.2) по своей сути дополняют традиционные встроенные операторы (+, -, *, ¸ ...) и функции (sin, cos, log ...), с помощью которых пользователь формирует выражения, значение которых присваивается константам, переменным и функциям пользователя.

Программа-скаляр – программа-вектор – программа-матрица

Эта тройка переменных может задаваться, естественно, и программно.

Рекурсия

Рекурсивная функция – это такая функция, которая вызывает сама себя в момент ее создания[22]. Рекурсия – очень мощный и удобный инструмент решения задач. Так, например, один из самых быстрых алгоритмов сортировки массива использует рекурсию. Вычислить детерминант квадратной матрицы также помогает рекурсия и т.д.

Языки программирования в своем развитии обычно проходят три стадии:

1. Рекурсия невозможна.

2. Рекурсия не разрешена, но применяется по принципу: «Если нельзя, но очень хочется, то можно». Так, на старых версиях языка BASIC рекурсия реализовывалась через оператор ON N GOTO, передающий управление программой на N-ю строку.

3. Рекурсия разрешена.

Mathcad вторую стадию проскочил (условно проскочил – это мы еще отметим, разбирая рис. 6.13).

И вот уже трещат морозы

И серебрятся средь полей...

(Читатель ждет уж рифмы розы;

На вот, возьми ее скорей!)

Читатель ждет уж примеров рекурсии в среде Mathcad? Скорее всего, нет. Традиционные примеры (розы-морозы) ему оскомину набили. Но мы попробуем что-нибудь свеженькое. Например, двустороннюю (ретроспективную) рекурсию.

Как запомнить число e (основание натурального логарифма) с девятью цифрами после запятой? Очень просто – две целых семь десятых плюс два раза Лев Толстой – 2.718281828, то есть к числу 2.7 нужно приписать два раза год рождения классика (1828). Остается самая малость – запомнить, в каком году родился Лев Толстой, или, на худой конец, сообразить, что это случилось в прошлом веке[23], чтобы вспомнить хотя бы три знака числа e после запятой: 2.718. Ретроспектива, обращенная в XIX век, поможет запомнить довольно-таки точное значение одной из фундаментальных констант математики.

Как запомнить, что факториал нуля равен не нулю (типичная ошибка), а единице? Очень просто. Нужно применить ретроспективный метод поиска факториала числа: сообщить машине факториал какого-либо положительного числа N (5! = 120, например) и то, что факториал предыдущего числа N-1 равен факториалу первого (N!), разделенному на N. Факториал пяти (120) – это такая же тривиальная истина, как и то, что Лев Толстой родился в XIX веке, а грубая оценка числа е – 2.7.

Размерность

По знаменитой формуле Н.Вирта программа – это сумма алгоритма и структуры данных. Алгоритм программы в среде Mathcad задается нажатием десяти кнопок на панели программирования (рис. 6.2), отвечающих за циклы, альтернативы и прочее. Структура данных в среде Mathcad также проста. Там есть только вещественные переменные двойной точности, которые могут превращаться в комплексные или целочисленные, группироваться в векторы и матрицы (простые и вложенные), принимать, если надо, текстовые значения.

Remake

В седьмой части этюда автор расскажет в стиле римейк об особенностях языка Mathcad.

Почему римейк? Во-первых, см. предисловие. Во-вторых, у автора сохранился файл с текстом статьи «Turbo Pascal 7.0. Взгляд со стороны» (КомпьютерПресс, № 7’93), которая и подвергается римейку (remake – переработка). В-третьих, язык Mathcad, как и язык Pascal, оказался окутан паутиной старых догм[33]

структурного программирования, о которых писалось в упомянутой статье. Это делает римейк не только простым, но уместным и естественным.

Итак, remake.

Попробуем на простых примерах показать, что ввод в язык Mathcad операторов break, continue и return (см. выше) – только полшага в сторону повышения гибкости управляющих конструкций этого языка программирования.

Проблема метки (English version of text)

Проблему метки, вернее, проблему избавления от метки, мы рассмотрим на примере решения старинной английской задачи о рыбаках и рыбке:

«Три рыбака легли спать, не пересчитав и не поделив улова. Ночью один из рыбаков проснулся и решил уйти, забрав свою долю. Но число рыб не делилось на три. Тогда он, не долго думая, выбросил одну рыбку, а из остатка забрал треть. Второй и третий рыбак поступили аналогичным образом – ушли по-английски и по-джентельменски, выбросив по одной рыбке и оставив спящим товарищам четное число рыб. Спрашивается, какое минимальное число рыб в улове отвечает условию задачи».

Пусть читатель сначала попробует решить эту задачу без компьютера. Компьютер же мы привлечем к этой работе для двух целей. Во-первых, на задаче о рыбаках и рыбке мы рассмотрим некоторые методы структурирования

программ в среде Mathcad – методы освобождения программ от меток и «втискивания» их в узкие рамки структурных управляющих конструкций, описанных выше (см. рис. 6.2). Во-вторых, мы покажем, что задача о рыбаках и рыбке до сих пор решалась неправильно...

Эту задачу в среде Mathcad можно решить, не прибегая к средствам программирования.

Золотое сечение

Программа на рис. 6.26 ищет минимум функции одной переменной методом золотого сечения[41]. В ней используется вспомогательная функция с именем Зол_Сеч, позволяющая отрезок a-b (отрезок неопределенности) поделить в золотом соотношении. Вывод этой функции через решение уравнения золотой пропорции средствами символьной математики (см. этюд 7) представлен в пункте 1 рис. 6.26.

Силы Кориолиса

На рис. 6.27 представлена созданная с помощью программирования функция minimum, возвращающая координаты точки минимума функции многих переменных (ее имя – аргумент y) и начинающая поиск от начальной точки приближения (вектор x). Алгоритм поиска минимума прост. От точки начального приближения по всем координатам делается шаг D (третий аргумент функции minimum). В новых местах[44]

вычисляются значения минимизируемой функции. Туда, где функция имеет минимальное значение, делается переход, данная точка становится новой точкой приближения к минимуму, а все вышеописанные действия («ощупывание» функции вблизи точки приближения) повторяются. Если окажется, что вблизи новой точки приближения все новые значения функции увеличиваются, то шаг поиска (D) уменьшается вдвое, а все действия повторяются. Поиск заканчивается, когда значение D становится меньше TOL (системная переменная Mathcad, регулирующая точность вычислений).

Продолжение задачи о краске

Применение средств программирования позволяет по-новому решить нашу задачу о краске (см. рис. 3.11 в этюде 3). При единственности решений, оптимизирующих либо объем, либо стоимость краски, разливаемой в барабаны двух типов, можно найти не одно, а ряд решений, где объем меньше максимального не более, чем на 2%, а при поиске максимума цены – на 0.5%.

Задача о компьютерах

Для производства четырех видов компьютеров (С1, С2, С3 и С4) имеются[48]

комплектующие пяти видов. Необходимо спланировать выпуск компьютеров (найти значение переменных С1, С2, С3 и С4) так, чтобы:

их число было максимально;

их стоимость была максимальна.

Исходные данные по задаче сведены в таблицу:

№ компьютера		Стоимость (у. е.)		Число единиц комплектующих, идущих на один компьютер
				1		2		3		4		5
1		600		1		0		4		0		3
2		2500		1		0		8		0		8
3		25 000		0		1		0		4		15
4		60 000		0		1		0		8		64
Есть комплектующих:		100		20		500		100		1200

Подобная задача реально стоит перед людьми, собирающими компьютеры «на коленках» отверточным способом: челноки привезли детали: 1 и 2 – это, к примеру, центральные процессоры двух типов, 3 и 4 – микросхемы памяти, а 5 – платы связи с периферией; компьютеру нужно, конечно, и многое другое, но это другое (корпуса, винчестеры) имеется в избытке. Из комплектующих нужно собрать компьютеры, максимизируя вышеотмеченные целевые функции.

Трехсторонняя дуэль

А теперь автор представляет на суд читателя свою любимую задачу – задачу о трехсторонней дуэли. Вот ее условия.

Сэм, Билл и Джон договорились сразиться на дуэли втроем по следующим правилам:

жеребьевка определяет, кто стреляет первым, вторым и третьим;

дуэлянты располагаются на одинаковых расстояниях друг от друга (по углам равностороннего треугольника);

обмениваются выстрелами по очереди, определенной жребием, пока двое не будут убиты;

очередной стреляющий может стрелять в любого из живых.

Известно, что Сэм – снайпер и никогда не промахивается с данной дистанции, Билл поражает мишень в 80% случаев, а Джон – в 50%. Какова наилучшая стратегия для каждого из участников и каковы вероятности их выживания, если они следуют оптимальным стратегиям?

В этой дуэли у Сэма и Билла могут быть две тактики поведения. Нулевая – это когда стреляющий ничего не знает о меткости соперников и целит в первого подвернувшегося. Первая – когда дуэлянту известно о том, кто как стреляет, и он метит в соперника с наивысшими стрелковыми качествами в надежде остаться tête-à-tête с наихудшим стрелком.

Джон может следовать и второй тактике. Чтобы получить наивысшие шансы выйти победителем из дуэли, он должен намеренно стрелять в воздух, пока двое его соперников живы. Ведь очередной стреляющий будет бить не в него, а в более меткого противника. После того как Сэм или Билл будет убит, Джон должен показать все, на что он способен. В такой ситуации его шансы выжить составляют 50%, если он остался наедине с Сэмом, и еще больше ¾ если с Биллом.

Участник дуэли, прежде чем выстрелить, должен, во-первых, определить самого меткого соперника, в которого нужно стрелять, руководствуясь первой тактикой поведения. Для этого предназначена функция Самый_меткий (см. пункт 2 на рис. 6.36), возвращающая номер противника с наивысшими стрелковыми качествами. В ней перебором всех участников дуэли (цикл for) учитываются, естественно, только живые противники (СтатусПротивник

= “жив”) и не сам стреляющий (Противник ¹ Стрелок).

A genuinely optimum fire bucket

(Translation into English by R.Girvin)

(Russian Text)

This optimization task was easily manageable either numerically (see Etude 2) or analytically (see Etude 7). In those, we learned how to maximise the volume of a bucket given a chosen manufacturing technology: cutting a sector from a metal disk and folding the remainder into a cone. But that way the bucket lost not only optimality, but also the status of bucket: it turned into a fire bowl! It was also impossible to put on a floor, and would be useless for any purpose except as a Vietnamese hat. In our rush for Number (the volume of the bucket) we have lost Essence (the function of a bucket, its capacity for conveniently carrying liquid).

The author recalls a cartoon film based on a Norwegian fable about a goat that learned to count, and decided to count all the farm animals: "I am one; the hen is two; the pig is three, etc." But as all the animals were moving around, the process soon turned into uproar. "Oh, have you counted me?!" "Keep still, or else..!" But everything ended happily, both for the goat and the fable.

In this story, as with any other fairy tale, there's a deep wisdom. It's necessary for us to count things, but as we interact with them we can run into a conflict. Not only does Nature dislike sharp corners, but also enumeration, which in a number of cases simply kills her. This can be observed not only in biology and physics, where the tools of knowledge frequently unrecognizably spoil the object of research, but also in computer science. This applies not only when applying computers to natural sciences applications, but also when applying computers to computers.

To establish a diagnosis, a doctor has no need to know the exact numerical value for a patient's body temperature (36.6C, 38.9C, etc). It's enough to express the thermometer indications by ranges, on which 'medics' have agreed beforehand: "low", "normal", "raised", "mild fever", "high fever". The borders of these estimates, though precisely fixed, are nevertheless imprecise – 'fuzzy'. This comes not merely from modern representations in terms of fuzzy set theory (FST) but also in terms of practical reality: thermometer error, measurement technique, and so on. A graduate of a medical school can tell you, without even pausing to think, where the division between high and very high temperature lies. The skilled doctor can decide this without consciously thinking of the number, while diagnosing better than the beginner.

Even the parameters of patients that are expressed not in real numbers, but in a kind of binary – Wasserman test positive/negative, Koch bacilli present/not present, HIV positive/negative, etc. – have 'fuzzy' borders. Laboratory analysts know this well. If you glance in any therapeutic reference book, where the symptoms of illnesses are described, normally you won't see hard numbers for body temperature, arterial pressure, haemoglobin count, etc. You'll simply see a broad categorisation: "is raised", "is lowered", and so on. Perhaps this is why programs that output a diagnosis, based on patient parameters entered into a computer, have not received wide practical application. One of difficulties in this area is translation of the parameter (a number) into a symptom (a category).
There's a generally accepted identification of three recent revolutions in programming: structural, object-oriented, and visual. But this revolutionary zeal focused more on the programs (the art for its own sake) and virtually neglected the point of programming: the models of the real world, the properties, and the events programs are simulating. Moreover, in retrospective we can see certain counter-revolutions: for example, the decline of analogue computers in favour of digital engineering. Recently, though, there has been a renaissance through the revival of principles of analogue modelling on modern digital computers (for example, the MathConnex environment included with Mathcad 7 and 8 Pro: see Appendix 7). It can similarly be seen in the technology of visual programming, where the former analogue control elements – adders, integrators etc. – are reconstructed.
But the virtual nature of these neo-analogue machines means also their strict determinism, and this brings not only positive, but also negative consequences. The principles of FST have been in programmers' hands for a long time – literally. The computer mouse reacts to two events: a click, and a double click. What, actually, is the difference one double click and two single? The duration of the pause between clicks. Expressed in non-technical language – "very short", "short", "long", etc.) this is a typical example of sets with 'fuzzy' borders. How much time is needed to increase a short pause to turn it into long, so that the double click breaks up into two single? How many handfuls of grain make a heap?


At the peak of the structural programming revolution, when in all the programming 'temples' the keyword GOTO was anathema, you frequently heard such statements as: "It's practically impossible to teach good programming to students originally taught BASIC; as potential programmers they're crippled intellectually, without hope of a cure." There were also broader warnings such as "Caution! Employment in programming is a dead end career. Don't think that having learned to program, you'll achieve anything in life".
It's as if traditional programming forces the programmer to look at the Technicolor world through monochrome glasses: a binary variable can take only two values (yes/no), and a real variable, values anywhere in a stipulated range strictly determined by the length of the mantissa. The truth lies somewhere between. The extreme points of view aren't useless – they are like book-ends that stop it sliding beyond defined extremes. The intermediate truths are termed 'fuzzy'. So one might say, "If you want to learn about the world (which is fuzzy, and unquantifiable) and to deal with it, beware of the traditional programming languages and mathematical programs with their strict determinism."
But we shall return to our problem of the fire bucket, and try to solve it using FST techniques and the opinions of people (who – thank goodness! – don't need such a rigmarole to use a simple device to escape being roasted).
Let's carry out an original poll and learn as much as we can about the parameters of an optimum fire bucket: its most convenient geometry (radius of the base of the cone to the height) and its optimum volume (the weight of the filled bucket). These can then be expressed as FST rules. How much water can you add to a bucket before it turns from light to heavy? How much can you increase or reduce the radius, or the height, of a bucket before it stops being convenient? These statements are typical definers of fuzzy sets. In the Mathcad environment, as well as in other popular packages, there are no variable types for storing such objects. But nevertheless we'll try to solve the given problem (see figures 6.41, 6.42, 6.43, 6.44 and 6.45 – a solution developed with B. Usyenko). Let's break it down into steps.



Fig. 6.41. Optimum radius of fire bucket
Step 1 (fig. 6.41). The matrix ?r stores people' s views about the optimum (most convenient) base radius r of a conical fire bucket, expressed in millimeters. This data could be gathered by making buckets of various geometries, giving them to people to try out, and then asking for estimates on a scale:
convenient (1);
more convenient than inconvenient (0.67);
more inconvenient than convenient (0.34);
inconvenient (0).
It would be possible to have more options within the range 0-1. In step 1 we have a limited familty of points, but these also could be increased; there are as many opinions as people. Readers can ask all their friends, and add new columns to the matrix [?r]
Step 2. The survey data is processed by the least squares method (see Etude 4). We can see that the data approximately fits a normal distribution curve (see figs. 6.41 and 6.42). The idea of a 'membership function' ?r for the radius of the bucket is one of the basic concepts of FST. In normal mathematics it would be considered that a certain size either belongs, or does not belong, to a particular set; in FST it's permissible to say that the size belongs to the set to some extent
(so many percent).
Step 3. The statistical processing is completed and plotted.

Fig. 6.42. Optimum height of a fire bucket
Steps 4-6 (fig. 6.42) repeat steps 1-3, but for a second parameter of the bucket, its height.

Fig. 6.43. Optimum volume of a fire bucket
Steps 7-9 repeat steps 1-3 and 1-6 for the third important parameter of the bucket, its volume (or weight – they're proportional). This is based on human estimates:
bucket is light (1);
bucket is more light than heavy (0.67);
bucket is more heavy than light (0.34):
bucket is heavy (0).
The survey data is processed as before, but using a "one-sided" cumulative distribution curve (see item 9 in a fig 6.43). (When designing technical systems, such parameters wouldn't be based on a survey but on figures provided by experts to the decision-makers).



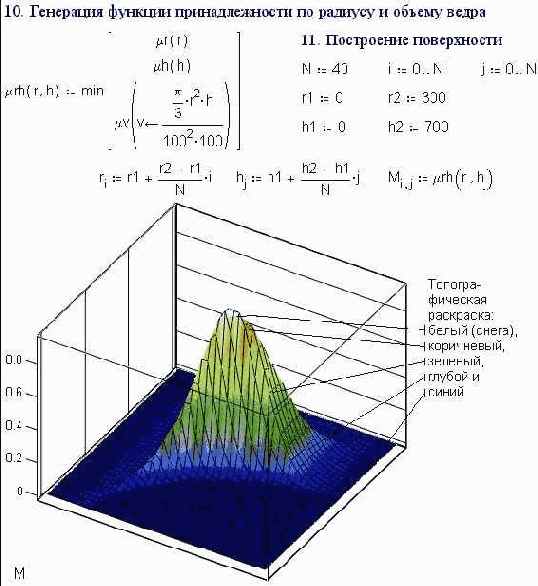
Fig. 6.44. the "Rotated" optimum fire bucket
Step 10 in fig. 6. 44 is the nucleus of the solution of our: in this, a two-parameter membership function is generated by the merging (akin to multiplication) of two single-parameter membership functions.
In FST there are no traditional concepts of addition, subtraction, multiplication etc.(those represented by the mathematical operators "+", "-", "×" etc. in the Mathcad environment). In FST, multiplication (crossing of sets – logical AND) is replaced with an operation of searching for a minimum; and addition (merging of sets – logical OR) by searching for a maximum. The mathematics of precise sets is a special case (a subset of the mathematics of fuzzy sets) where these operators/functions are genuinely equivalent. This means that in the Mathcad environment, where there are no built- in AND and OR operators, we can create equivalents using the min and max functions we described in Etude 3.
In our task the membership function mu_rh is generated by the fuzzy addition (min) of the functions mu_r, mu_h and mu_v. That is, the fuzzy set "the convenient bucket " is the intersection of three other fuzzy sets: "convenient radius of bucket" (step 1), "convenient height of bucket" (step 6) and "a not heavy bucket" (step 9).
Step 11. The top of the 'mountain' – the surface plot of function mu_rh – is the point where the parameters of most convenient fire bucket lie.

Fig. 6.45. Designing the optimum fire bucket
Step 12 (fig. 6.45). Searching for the maximum of the function mu_rh in the Mathcad environment can be done in various ways (see Etudes 2 and 3). We'll proceed this way: we'll imagine metal disks of various radius R (from 10mm-500 mm with a step of 1 mm) and cut each size into 2 to 10 identical buckets. This gives a large variety of bucket sizes and geometries, and we'll consider the optimum (the most convenient) bucket to be the one for which the membership function mu_rh is maximised.


Even the reader who hasn' t been paying much attention will notice some discrepancies and simpiflications in our analysis of this task. Three of them are:
Unlike our theoretical bucket, a real one is never filled up right to the brim ("what counts as full?" defines another fuzzy set).
The author has only loosely defined, and often confused, such concepts as "volume", "weight", and "weight of bucket".
We haven't taken into account the weight of an empty bucket, and also the material from which it is made.
However it is merely necessary to glance again at the diagrams illustrating fuzzy sets in figs. 6.41, 6.42 and 6.43
to understand a major virtue of applying FST to decision-making tasks. Our solution works in isolation, so it's possible to express the essence of a task disregarding various minor variables: the density of water, weight of the empty bucket, degree of filling, etc. This feature is now realized, for example, in automatic control systems, where regulators based on FST rules are more 'attentive' to the basic signal and less susceptible to noise. It turns out, though it seems paradoxical, that the traditional 'precise' control algorithms qualitatively lose out to 'fuzzy' ones, or are their special cases. In the field of automatic control theory, a certain stagnation could be seen until recently, as any new algorithms couldn't be compared to the older Proportional Integral Derivative (PID) control algorithm. The principles of PID control can be seen in the procedure for a bank's credit check on a client applying for a loan. The banker, in assessing the decision, considers:
1)      The sum of money in the client's account (this is the proportional component: the richer the client, the larger the loan that can be offered);
2)      The average sum in the account over, say, the last five years (the integrated component; checking this ensures that the client didn't borrow a million pounds the day before, to create the illusion of solvency); and


3)      The rate of change of the account (the differential component, showing whether the client's business is on the rise or decline);
It's possible to take into account other factors, but three is a nice number!
The PID-control algorithm has imperceptibly become something of a fetish. Fuzzy management cames as a fresh breeze in the theory of automatic control, whose basic rules are now open to review. To be sure, there are other opinions. Some scientists believe that the use of FST in automatic control, and cybernetics in general, is just replacing one uncertainty with another ("trying to stitch soapsuds", the Russian expression goes) and that's all there is to it. Sceptics explain away the observed improvement in control quality to our devoting more attention to regulator technology (as if the ritual of attention could improve performance). Besides some researchers believe that FST, since it dates back 30 years (it was devised by the Iranian-American Dr Lotfi Zadeh at UC/Berkeley in the 1960s) is old and best forgotten.
Actually, the skip from a task about a tripartite duel to one about an optimum bucket wasn't entirely casual. Traditionally, precise sets are illustrated by circles with sharply delineated borders. Fuzzy sets are drawn as circles formed of separate dots, with a high density at the centre and thinning to zero (as if evaporating) towards the edges. Such 'fuzzy set' images can be seen on a firing range wall where targets are hung. The bullet traces form a probability distribution, whose mathematics is well-known. It appears that the theory for working on fuzzy sets, as probabilistic distributions, has already existed for a long time...
We keep talking about fuzzy sets. But are they – mathematically – actually sets? To be consistent, it's necessary to ascertain that the fuzzy set has elements (fuzzy subsets, fuzzy sub-subsets, etc). We'll return to a classical example: a heap of grain. An element of this fuzzy set will be, say, a million grains. But a million grains is not a precise element: it's a fuzzy subset. If you count out grains, whether manually or automatically), it's no wonder that you might mistake, say, 999 997 grains for a million. In FST terminology, you could say that the element 999 997 has a 'membership value' 0.999997 for the fuzzy set {a million grains}. Besides, even "a grain" is not a precise element, and is another fuzzy subset: it might be a high-grade grain, but there are also underdeveloped grains, grain fragments, and bits of husk. Depending which way you decide, you might count one grain as two, or vice versa.


The fuzzy set isn' t very easily accommodated in the digital computer with classical data constructs: elements of a file (a vector) should be new files of files (composed of vectors and matrices, in the case of Mathcad). The classical mathematics of precise sets (number theory, arithmetic, etc) is rather like a hook, with the help of which we anchor ourselves on the slippery and fuzzy environmental world. And a hook is a rough implement, quite often damaging what it's embedded in. The terms describing fuzzy set membership values (there are plenty in this book and others – "much", "some", "a few", and so on) are difficult to make into programming statements because they're contextually dependent. It's one business to say, "Give me a few sunflower seeds" to someone with a cupful, and another to say the same to a driver hauling a lorryload.
Whether it is possible to see a certain crisis in theory and practice of programming connected with contradict between precise structure of the programs (data) and fuzzy world? Is it necessary to develop fuzzy programming languages for implementation fuzzy algorithms that accommodate fuzzy data? Opinions vary. In the author's view, programmers (and they have the last word) have learned poorly how to cram the fuzzy world into the strictly determined computer. Figs. 6.41, 6.42, 6.43, 6.44
and 6.45 are an example.

По-настоящему оптимальное пожарное ведро (English version of text)

Эта оптимизационная задача хорошо решается и численно (см. этюд 2), и аналитически (см. этюд 7). В ней под оптимизацией мы понимали максимизацию

объема ведра при выбранной технологии его изготовления (вырезание сектора из круглой заготовки). Но при этом ведро теряло не только свою оптимальность, но и свое звание ведра: оно превращалось в пожарный тазик (его тоже нельзя поставить на пол и использовать не по назначению) или во вьетнамскую шляпу. Мы гнались за Числом (объем ведра) и потеряли Суть (функцию ведра – емкость для удобной переноски жидкости).

Тут автору вспоминается мультфильм о козленке, который научился считать и всех встречных-поперечных пересчитывал: «Я – это раз, петух – это два, свинья – это три и т.д.» У козленка из-за этого со всей пересчитанной живностью возникали крупные неприятности: «Ах! Ты меня сосчитал?! Ну, держись!» Но все кончилось хорошо. На то она и сказка.

В этой истории, как и в любой другой запоминающейся сказке, есть глубокий смысл. Стоит нам что-то пересчитать, как мы вступаем с этой пересчитанной субстанцией в глубокий конфликт. Природа не любит не только острых углов, но и счёта, который в ряде случаев просто убивает ее. Это можно наблюдать не только в биологии и физике, где инструменты познания часто неузнаваемо портят сам объект исследования, но и в computer science. И не только в области приложения компьютеров (счёта, грубо говоря) к решению естественнонаучных задач[54], но и в области применения компьютеров к самим компьютерам.

Врачу для установления диагноза незачем знать числовое значение температуры тела больного – 36.6, 38.9 и т.д. Достаточно выразить показания термометра диапазонами (категориями), о которых медики договорились заранее – «температура пониженная», «нормальная», «повышенная», «высокая», «очень высокая» («жар»)[55]. Границы этих оценок хоть и четко зафиксированы, но тем не менее размыты – «пушисты». Это определяется не только современными представлениями ТНМ, но и погрешностью самого термометра, методикой измерения температуры и др. Выпускник медицинского вуза не задумываясь скажет вам, где лежит граница между высокой и очень высокой температурой. Опытный же врач может этого и не знать, хотя диагнозы он выставляет не хуже начинающего доктора. Даже параметры больного, выраженные не в вещественном, а в булевом виде (реакция Вассермана, наличие палочки Коха, анализ на СПИД и т.д.), имеют «пушистые» границы. Об этом хорошо знают лаборанты, проводящие анализы. Если заглянуть в любой справочник терапевта, где описаны симптомы болезней, то, как правило, конкретных чисел (температура тела, артериальное давление, содержание гемоглобина в крови и т.д.) там не увидишь. Одни слова – повышено, понижено и т.д. Программы выставления диагноза по введенным в компьютер параметрам больного не получили широкого практического применения. Одна из трудностей в этом деле – перевод параметра (числа) в симптом (категорию).

Принято выделять три революции, переводившие программирование на новые уровни: структурное, обьектно-ориентированное и визуальное. Но эта революционность была больше обращена на программы
(искусство ради искусства) и почти не касалась объекта программирования – тех моделей реального мира, свойства и события которого программно имитируются. Более того, ретроспективный взгляд может уловить и некую контрреволюционность в отказе, например, от аналоговых вычислительных машин и переход к цифровой технике. Хотя в последнее время здесь наблюдается какое-то подобие ренессанса – возрождение принципов аналогового моделирования на современных цифровых компьютерах (пример – среда MathConnex в составе Mathcad 7 и 8 Pro: см. приложение 7). Это можно отметить и в технологии визуального программирования, где воссоздаются прежние элементы управления (controls) – аналоги сумматоров, интеграторов и др. Но виртуальность этих неоаналоговых машин подразумевает и их строгую детерминированность (четкость), что влечет за собой не только положительные, но и отрицательные последствия. Сами же принципы ТНМ давно уже у программистов под рукой. В буквальном смысле. Мышка компьютера реагирует на два события – щелчок (click) и двойной щелчок (double click). А чем, собственно, один двойной щелчок отличается от двух одинарных? В длительности паузы между щелчками. Если ее выразить на языке человеческого общения (очень короткая, короткая, длинная и т.д.), то это будет типичным примером множеств с «пушистыми» границами. На сколько нужно увеличить короткую паузу, чтобы она превратилась в длинную и чтобы двойной щелчок распался на два одинарных? А сколько зернышек нужно добавить в горсть, чтобы она превратилась в кучу[56]?
В разгар структурной революции, когда во всех программистских «храмах» предавали анафеме ключевое слово GOTO[57], часто можно было услышать такую фразу: «Практически невозможно научить хорошо программировать студентов, ориентированных первоначально на BASIC: как потенциальные программисты они умственно оболванены без надежды на исцеление». Встречались и более категоричные предупреждения типа: «Осторожно! Занятие программированием может лишить вас будущего. Не думайте, что научившись программировать, вы чего-то добьетесь в жизни». Традиционное программирование как бы заставляет программиста смотреть на многоцветный мир сквозь черно-белые очки: булева переменная может принимать только два значения (да-нет), а вещественная – строго определенное в оговоренном диапазоне с фиксированной длиной мантиссы и т.д. Истина лежит посередине. Но и крайние точки зрения не бесполезны – они как бы подпирают истину с двух сторон, не давая ей скатиться к крайностям. Да и сами истины в чем-то «пушисты». А одна из них может звучать так: «Если хочешь познать мир (нечеткий, «пушистый», бесчисловой) и управлять им, то опасайся традиционных языков программирования и математических программ с их строгой детерминированностью».


Но вернемся к нашей задаче о пожарном ведре и попытаемся решить ее уже с привлечением аппарата ТНМ и с учетом мнения людей, которым – не дай Бог! – придется воспользоваться этим нехитрым средством пожаротушения.
Проведем своеобразный опрос общественного мнения и узнаем как можно больше о параметрах оптимального пожарного ведра: о его удобной[58] геометрии (радиусе основания конуса и высоте) и о его оптимальном объеме (о весе ведра с водой). Вот здесь-то и проявятся во всей своей красе положения ТНМ. Сколько нужно добавить в ведро воды, чтобы оно из легкого превратилось в тяжелое? На сколько нужно увеличить или уменьшить радиус или высоту ведра, чтобы оно перестало быть удобным? Вот эти сколько и являются типичными представителями нечетных множеств. В среде Mathcad, как и в других популярных пакетах, нет типов переменных для хранения таких величин. Но мы тем не менее мы постараемся решить поставленную задачу (рис. 6.41-6.45 – задача решена совместно с В.Усенко). Разберем ее по пунктам.

Tutti-frutti

Ниже приводится ряд программ, написанных на языке Mathcad и решающих самые разнообразные задачи (tutti-frutti по-итальянски – всякая всячина): оптимизация, головоломка, статистика, теория вероятностей...

A and B sat on a pipe

We can imagine A and B sitting down to pass the time of day – in our case, not on a simple pipe, but on a fire bucket. We'll now explain the 'universal' meaning of these parametrical factors A and B (more correctly A_r, B_r, A_h, B_h, A_v and B_v) included in the approximation expressions of stages 2, 5 and 8 (fig. 6.41-43).

Viewing the fuzzy set as a statistical distribution, A represents the 'spread' of the distribution, and B the parameter value giving the peak of the distribution. Imagine we carry out a global statistical experiment. We measure for all adult humans some parameter – weight, height, intelligence, etc – whether represented numerically or estimated by some criterion (genius, talented, very clever, simply clever... down to idiot). The data points we shall transform into a curve (see sections 1-3 in figures 6.41, 6.42

and 6.43) where the X-axis is the measured human parameter, and the Y-axis the percentage of people with a given value of that parameter. We carry out this statistical exercise separately for men (M) and women (F). What do we get?

Case 1: AM = AF, but BM > BF:

Curves turn out like this for parameters – such as height, weight, strength of muscles, etc – pertaining particularly to men rather than women. This is related to evolution: sexual dimorphism is related to the general trend in species size. If the male body is larger than the female, the next generation tends to be larger. With spiders, for example, the male is much smaller than the female, and so – thank God – spiders are smaller now than the geological past.

Case 2: AM < AF, but BM = BF:

The curve looks like this for a parameter – intelligence – whose importance applies equally to both sexes, and has not varied for millennia. Many consider it quite proven, that if modern humans were suddenly stripped of education and culture, we would be no more intelligent (maybe even less so) than the Ancient Greeks. It's not known why, but there is a greater spread for men: there are more men of genius (Nobel prizewinners, inventors, writers and artists – at the right edge of the diagram) only because there are also more men of extremely subnormal intelligence (the left edge). The average woman is cleverer the average man: the centre of the "female" distribution is raised at the expense of a smaller spread. The areas of both curves is, however, identical: no offence intended to anyone, but we believe that the Lord God or Nature (whichever you believe in) has shown consideration in distributing intelligence equally to both halves of humanity.

We can try to apply the theory of fuzzy sets, as described in Etude 3, to the problem of computer piracy. The law divides all people into two precise sets: {legal users of programs} and {illegal users – pirates}. In real life, it's much more complex: computer users fall into two fuzzy sets, with a great variety of motives. At one extreme are people trading 'black' disks at Gorbushka (the left-hand axis of the diagram above); at the other are those who work only with legal copies and have never broken any license agreement (the right-hand axis). Again, it's possible to construct a humpbacked statistical curve, this time above an axis "sinner ... saint" describing the condition of the computer market in a particular country. Where does the maximum of this curve lie, and how is it shifting with time?

A и B сидели на трубе

Сидели они не на простой трубе, а на пожарной, точнее – на пожарном ведре: сейчас будет рассказано об «общечеловеческом» смысле параметрических коэффициентов A и B (вернее Ar, Br, Ah, Bh, Av и Bv), входящих в аппроксимирующие выражения пунктов 2, 5 и 8 (рис. 6.41-43).

Давайте проведем глобальный статистический эксперимент – у всех взрослых людей на земле измерим какой-либо параметр: вес, рост, ум и т.д. ¾ словом все то, что можно измерить числом или оценить критерием (гений, талант, очень умный, просто умный... совсем дурак).

Полученные точки превратим в кривые (см. пункты 1-3 на рис. 6.41-43), где по оси X отложим параметр человека, а по оси Y – процент людей с данным параметром. При этом статобработку проведем отдельно для мужчин (м) и женщин (ж). Что мы получим?

Случай 1: Ам

= Аж, но Вм > Вж:

Такие кривые получаются для тех параметров, значение которых у мужчин больше, чем у женщин (рост, вес, сила мышц и т.д.). Это связано с эволюцией – если мужская особь крупнее женской, то новые поколения укрупняются. У пауков, например, самцы намного меньше самок – пауки сейчас, слава Богу, более мелкие, чем в доисторические времена.

Случай 2: Ам

< Аж, но Вм = Вж:

А так будут выглядеть кривые для параметров, значения которых у человека за последние несколько тысяч лет не менялись – ум, например. Многие вполне обоснованно полагают, что современный человек, если убрать налет образованности и культуры, ненамного умней древнего грека. Среди мужчин гениев[66]

(нобелевских и прочих лауреатов, великих изобретателей, писателей[67]

и художников – см. правый край графика) больше лишь потому, что и дураков среди мужчин достаточно (левый край графика). Но средняя женщина умнее среднего мужчины – центр «женской» кривой приподнят за счет меньшего разброса по краям: площади фигур под графиками одинаковы – никого не обижая, будем считать, что Господь Бог или Природа (кто как для себя считает) одинаково наделили умом обе половины человечества.

Теорию нечетких множеств, как уже было отмечено в этюде 3, можно попытаться приложить и к проблеме компьютерного пиратства. Закон делит всех людей на два четких множества: «множество легальных пользователей программ» и «множество нелегальных пользователей (пиратов)». В реальной жизни все намного сложней: нечетких множеств людей, причастных к компьютерам, великое множество (извините за тавтологию). Есть множество торгующих на «Горбушке» «черными» дисками (левый край оси – см. графики выше) и есть множество тех, кто принципиально работает только с легальными копиями и никогда не подаст руки согрешившим – нарушившим какое-либо лицензионное соглашение (правый край оси). Можно опять же над осью «грешник-праведник» построить горбатые статистические кривые, описывающие состояние компьютерного рынка в конкретной стране. Где находится максимум этой кривой, куда и с какой скоростью он перемещается во времени?

Философско-религиозный аспект проблемы

Естествоиспытатель, желающий познать окружающий мир, не может прямо обратиться к Создателю

– к Богу или к Природе, кто как для себя считает, а должен задавать вопросы самому объекту исследования, то есть должен проводить эксперимент – вносить в объект возмущения и фиксировать реакцию на них.

У программы есть авторы. Их имена далеко не всегда указаны на коробках, дисках и в документации, но они есть. Следовательно, какие-либо эксперименты над программами излишни. Возникающие вопросы нужно адресовать либо документации, либо самим авторам. Но! Если пользователю, к примеру, потребуется уточнить, в градусах или в радианах измеряется аргумент синуса, то он не будет рыться в документации, а просто напишет x:=sin(90) и посмотрит, чему окажется равна переменная x. Подобные эксперименты пользователи ставят ежечасно, обращаясь к документации только в особо сложных случаях и, как правило, не находя там ответа. Обращение же к Создателю проблематично. На hot-line сидят не авторы, а продавцы программ, что, как понимает читатель, далеко не одно и то же. Консультант фирмы скорее всего попросит вас перезвонить через пару дней, за которые он проведет свой эксперимент над программой и попытается найти ответ. Да и обращение к самому автору часто ничего не дает, так как он уже забыл свое детище и всецело поглощен новым проектом. Если даже это не так, то автор может и не помнить всех свойств, а уж тем более нюансов своего творения.

Из-за этого при работе с программами пользователь часто забывает, что это продукт ума и рук человеческих (Природа сотворенная), полагая (на уровне эмоций), что это плод работы анонимного и недоступного Создателя (Природа творящая), у которого нет hot-line. Здесь, по-видимому, и кроется философское объяснение

(но ни в коем случае не оправдание) широкого распространения нелегального копирования программ. Имеются в виду не китайско-болгарские компакт-диски типа «Все для офиса» – воровство есть воровство[68]. Речь идет об относительно честных людях, ставящих на свой компьютер программу с того же лазерного диска, чтобы познать Природу и передать свои знания, например, студентам.

Можно считать, что Создатель, бросив сверху яблоко и угодив им по Ньютоновой голове, приоткрыл нам одну из тайн своего Божественного Замысла. Заслуга гения (Ньютона) – в умении оказаться в нужном месте в нужное время[69]. Программы (и не только гениальные) как бы тоже падают к нам сверху, и человек не обязан за них платить сумасшедшие по российским меркам деньги. Отсюда и живучесть идеи shareware, которой противятся в первую очередь продавцы, а не авторы программ.
Как говорится, есть мнение, что Бог создал по своему образу и подобию не только человека, но и компьютер. Написание для него программы – это вдыхание души в безжизненное нагромождение железок. Торговля телом (трансплантация органов, переливание крови или, наконец, проституция) – реалии наших дней. Покупка и продажа души встречается только в сказках и художественной литературе (история Фауста, например). Приобретая программный продукт, мы опять же покупаем только «тело» – диски, документацию, информацию и скидки по новым версиям, а главное – послепродажный сервис.

Общекультурный аспект проблемы

Откройте первую страницу любого западного издания и вы увидите предупреждение о том, что эту книгу (ее отдельные главы или страницы) запрещено копировать. Автор сначала написал «и вам бросится в глаза грозное предупреждение», но потом заменил на нейтральное «вы увидите». Все прекрасно понимают, что имеется в виду копирование в коммерческих целях. Как на Западе, так и у нас в библиотеках вполне легально стоят копировальные аппараты, на которых «ксерят» книги и журналы от корки до корки, исключая разве что ту самую страницу с грозным, а по сути пустым предупреждением. Снимать копии с печатной продукции любыми доступными способами (выпиской цитаты в тетрадку, например) можно в образовательных и научных целях. Более того, если кто-то препятствует такому способу распространения информации, то это расценивается как прямое нарушение прав автора. Не авторских прав[70], а именно «прав автора». За этой стилистикой скрывается то, что авторскими правами почти всегда распоряжается не автор, а издатель. Права же автора, это как права человека, которые «от Бога» и которые невозможно передать кому-либо. Появление на рынке «черных» копий книги расстраивает обладателя авторских прав. Автор же (обладатель прав автора) сначала радуется этому, а потом уж огорчается по поводу потери будущей и, как правило, эфемерной прибыли[71]. Размытость границы между коммерческим и некоммерческим использованием копий можно видеть и в другом. Аспирант «наксерил» чужих статей, слепил из них диссертацию (скажем мягче – часть диссертации), получил ученую степень, а через нее – высокооплачиваемое место на фирме или в университете. Даже если слово «слепил из них» заменить на «которые помогли ему написать», то суть дела не меняется: знания – это самый дорогой товар на цивилизованном рынке.

Такой подход к книжной продукции пользователи ЭВМ (а это сейчас самая читающая публика – в метро мелькает не только дамский роман, но и какой-нибудь User’s Guide или «Excel для «чайников») перенесли и на программные продукты (продукция, продукты – это все рыночные термины). Изучить программу так же интересно и полезно (в общекультурном, образовательном плане), как и книгу. Беда, а быть может, и счастье программ лишь в том, что копировать их намного проще, чем книги. Кроме того, даже самые гениальные программы, в отличие от классической литературы, умирают раньше срока завершения действия авторских прав. Пушкина или Шекспира сейчас кто угодно может издавать.

Милицейский аспект проблемы

В печати то и дело мелькают сообщения о том, что где-то на ВВЦ (бывшая ВДНХ), в Митино и у ДК им. Горбунова («Горбушка») ОМОН разогнал торговцев пиратскими CD-ROM с записями популярных программ для ЭВМ[72]. Первая реакция на это: «Наконец-то!» Но потом приходят другие мысли. Когда люди с автоматами наперевес проверяют документы у лоточников в подземном переходе, то девять прохожих из десяти думают не о том, что наводится порядок, а о том, что просто собирается дань. Десятый прохожий думает о том, что опять «заметут» всяких мелких сошек, а организаторы нелегальной торговли отделаются легким испугом. Боже упаси решать у нас какую-либо проблему чисто полицейскими мерами. До сих пор из этого ничего толкового не получалось, а если проблема и решалась, то выходил какой-то ГУЛАГ. Кроме того, здесь плавно выходит на первый план

Моральный аспект проблемы

Милицейские рейды на рынки программ, и это отмечалось в печати, были проведены по наводке сотрудников российских компьютерных фирм, увидевших на лотках незаконные копии своих программных продуктов. Сотрудников, заметим, профессионально выросших на тех же пиратских копиях, правда, чужих программ. Нелегально ставили они их на свои компьютеры, конечно, в общеобразовательных и в научных целях, но... см. выше. К милицейским рейдам, говорят, приложило руку и московское отделение одной знаменитой компьютерной фирмы. Той самой, за которой тянется длинный шлейф судебных процессов по поводу нарушения чужих авторских прав. Знаменитой фирме можно посоветовать сначала разобраться с вопросами об авторских правах на оконный интерфейс, а потом уже «стучать куда следует». Вы видели главу этой фирмы? Похож он на человека, которого обокрали?

Библейское предание говорит о том, что Христос спас неверную жену от самосуда толпы, призвав первым бросить в несчастную женщину камень того, кто сам безгрешен. У автора такое чувство, что какое-то подобие самосуда над несчастными отечественными пользователями программ пытается совершить наша пресса (глас толпы)[73]. При этом на одну доску нередко ставятся и торговец с «Горбушки», и вузовский преподаватель[74]. Да, и у того и у другого на руках нелегальные копии, но называть и, главное, судить их нужно по-разному, с учетом вышеизложенных аспектов. Торговцы с «Горбушки» вообще не имеют никакого касательства к закону об авторском праве. К ним нужно применять другие мерки и другие статьи закона – те, где говорится о нарушении правил торговли или даже о воровстве и разбое. Производители программных продуктов у нас в России (да и не только у нас) попали в какой-то заколдованный круг. С одной стороны, хочется защитить свои права всеми возможными средствами, а с другой – не имеешь на то морального права, ибо сам такие же, но чужие права неоднократно нарушал и будешь нарушать впредь – сын, например, дома скачивает с «черных» дисков игрушки.

Если программу воруют... Нет, камень бросать не будем и скажем по-другому. Если программу копируют без ведома автора или того, кому принадлежит copyright, то нужно не огорчаться, а радоваться. Автору, конечно, а не продавцу. Защищать же программу следует активными (хороший послепродажный сервис[75], электронный ключ, наконец), а не фискальными средствами. Аналогия из области адюльтера – пиратства на семейном фронте[76]. Если у вас красивая жена, то на нее засматриваются (и не только) окружающие. Бороться с изменами следует активными методами – подарки, признания, короче, хороший послесвадебный сервис, пояс верности (электронный ключ), на худой конец[77]. Слежкой тут делу не поможешь. Тем более противно, когда осуждают чужих жен, да еще пытаются при этом писать какие-то «залесские» декларации и статьи.

Автор, кажется, нашел для себя решение проблемы компьютерного пиратства. Считается, что нельзя быть немножко беременной. Но быть немножко честным в коммерческом использовании чужих программ, наверно, можно. Автор со своими коллегами разрабатывает программы для электростанций. Эта работа начиналась, естественно, с нелегального использования программ типа Turbo Pascal, Visual Basic и т.п. Но как только мы получили первые деньги за проданные программы, то пустили их не на зарплату, не на покупку нового компьютера, а на приобретение использованных инструментальных средств – даже тех, с которыми мы уже не работали[78]. Теперь у нас все коммерческие проекты базируются на легальных программах, образовательные же (автор работает в Московском энергетическом институте) – пока нет. Вернее, немножко нет: покупается (да и то не всегда – пусть в нас бросят камень) программа для одного компьютера, а устанавливается на все машины в учебном классе[79]. Но решение этой проблемы – дело времени. Россия либо окончательно увязнет в разного рода кризисах, либо наладит нормальную систему образования (здравоохранения, социального обеспечения и т. д.) с нормальным финансированием. Третьего не дано. А пока же неплохо установить мораторий не на использование нелегальных копий, а на осуждение тех, кто это делает в общеобразовательных и учебных целях, понимая при этом, что диапазон коммерческого использования чужих программ очень широк. На одном его конце аспирант, обрабатывающий экспериментальные данные на компьютере, а на другом организатор доставки и распространения «черных» лазерных дисков. Хотя это не самый страшный «черный» бизнес: радуйтесь, что торгуют «железом» и программами, а не настоящими винчестерами и наркотиками.
Чехов, по его собственному признанию, по каплям выдавливал из себя раба. Но ему даже в голову не приходила мысль попытаться насильно выдавить что-то гадкое из читателей. Чехов своими произведениями помогал им становиться лучше, только и всего. Давайте же выдавливать из себя по каплям (вычерпывать ведрами) компьютерного пирата. Делать это надо без истерик, без милицейских шмонов и тем более без стукачества, оставаясь наедине со своею совестью, поглядывая в свой кошелек и в Уголовный кодекс.


Автор боится, что проблема компьютерного пиратства у нас в стране решится чисто по-советски – через дальнейшее увеличение административного аппарата. Будет, например, создана компьютерная полиция, которая по примеру своих собратьев из налоговой полиции не сможет сунуть нос в миллиардные особняки, как грибы растущие в Подмосковье без всяких налоговых деклараций, или на оптовые рынки, отоваривающие пол-Москвы без каких-либо кассовых аппаратов. Попортить нервы предпринимателю-производственнику, еле-еле выживающему в нашем налоговом беспределе – это полиция может. Налоговая полиция должна вышибать двери не только у нелегальных бутлеггеров, но и в шикарных кабинетах начальства, отделанных на бюджетные средства. В первом случае нужно надевать бронежилет, а во втором – памперсы. Так вот, автор боится, что компьютерная полиция, если она будет создана, первым делом пойдет не на «Горбушку», а в какой-нибудь ВУЗ или НИИ, чтобы наложить штраф на вышеописанного аспиранта.
Часть полученного за книгу гонорара автор тратит на приобретение легальной версии текстового редактора, с помощью которого эта книга писалась. Но автор хочет быть с читателем откровенен до конца и сообщает, что программа будет куплена:
если на это хватит гонорара;
если не появится новая версия текстового редактора – покупать (или «воровать») придется уже ее;
если автор не передумает.
Другую часть полученного за книгу гонорара автор потратит на приз читателю, приславшему самую короткую программу перевода римского числа в арабское. Для «затравки» автор помещает в конце этюда программу перевода арабского числа в римское (см. первую половину рис 6.46).

Открытое письмо пирата в адрес компьютерных изданий (English version of text)

Открыв любой номер любого компьютерного издания, можно наткнуться на статью, касающуюся проблемы нелегального копирования и распространения программ. Данное письмо также затрагивает эту тему, но несколько в ином ключе. Здесь нет попытки кого-то осудить или оправдать. Автор просто пытается рассмотреть проблему в необычных аспектах: философском, религиозном, общекультурном, милицейском, моральном и даже... сексуальном.

Отладка Mathcad-программ

Каждый, кто когда-либо серьезно занимался программированием, знает, что написать программу можно за несколько минут. Но на поиск ошибки в ней могут уйти часы, дни, недели...

Английский эквивалент термина отладка – a debugging заслуживает отдельного разговора. A bug по-английски – жучок, а приставка de означает удаление. Сам термин debug дословно можно перевести как обезжучивание. Эта калька с английского не такая уж бессмысленная. Один из первых компьютеров стал барахлить из-за того, что в его электронных внутренностях запутался таракан, закоротил контакты, обуглился и, как некий связист-камикадзе, замкнул их, внеся тем самым изменения в электронную схему машины.

К сожалению, пакет Mathcad не оборудован штатными средствами отладки. А к ним обычно относят следующую тройку инструментов:

1. Трассировка программы (Trace), когда после ее запуска цветом или жирным выделением отмечаются выполняющиеся операторы. Так можно проверить соответствие порядка выполнения операторов задуманному алгоритму. Программу можно выполнять и пошагово – очередной оператор выполняется после нажатия программистом какой-либо оговоренной клавиши. При этом можно «заходить» или не «заходить» в функции или процедуры. Не заходят в них в тех случаях, когда они отлажены и оттестированы отдельно (заранее).

Система Mathcad, выполняя операторы документа, своеобразно трассирует их. Если какой-либо оператор выполняется достаточно долго (суммируются элементы объемного вектора, например), то он оконтуривается и штрихуется зеленым цветом. Это можно было бы назвать трассировкой, если такое выделение операторов велось бы и в теле программ с циклами и альтернативами. Но система Mathcad рассматривает программу как единый оператор (второй атрибут программирования) и не подсвечивает операторы в нем, а оконтуривает и подсвечивает всю программу: «Ждите ответа!»

2. Пошаговое выполнение операторов обычно сопровождают просмотром (Watch) текущих значений всех или некоторых переменных. При этом на дисплей выводится специальное окно, где отмечаются имена переменных, их тип, текущее значение и др.

3. Критические операторы (места) программы отмечают точками останова (BreakPoint), где компилятор прекращает выполнение машинного кода. После этого программист может просмотреть значения всех или некоторых переменных (см. выше), подправить программу и дать команду на ее дальнейшее выполнение (выполнять программу далее в нормальном режиме, пошагово или даже пустить вспять, если чувствуется, что ошибка случилась ранее отмеченного места).
Но повторяем, среда программирования Mathcad лишена каких-либо специализированных средств отладки. Объяснить и в какой-то мере оправдать это можно лишь тем, что программирование – это лишь вспомогательный инструмент при решении задач[80]. Но при отладке самой программы Mathcad, по-видимому, инструменты отладки использовались. Автор об этом узнал случайно, когда работал с самой первой бета-версией Mathcad 8, нажав правую кнопку мыши с курсором, помещенным на рабочем листе. Вот что появилось на экране дисплея (рис. 6.48): локальное меню с волшебным словом «Debugger»:

Оптимизация Mathcad-программ

Программист, написав и отладив программу, как правило, на этом не успокаивается и начинает ее улучшать – оптимизировать. Таким программистам можно посоветовать повесить на стене перед глазами такой листочек:

«За все нужно платить!»

 

«Лучшее ¾ враг хорошего!»

«Не до жиру, быть бы живу!»

Далее в тексте читатель будет встречать подобные тривиальные истины, некоторые из них он может также вывешивать в виде плаката[89].

Поговорим о том, что можно улучшить в программах – хотя бы в тех, которые помещены в этой книге.

Программы можно оптимизировать по разным параметрам. Вот три основополагающих:

Время выполнения программы;

Объем программы: место, занимаемое ею в ОЗУ компьютера, длина файла с исходным текстом программы, хранимого в архивной памяти.

Читабельность программы; степень ее открытости для изучения другими людьми и для доработки самим автором или кем-то другим.

Последнее качество в отличие от двух первых не так просто выразить числом, на которое можно целенаправленно влиять. Но мы уже рассмотрели понятие удобное

пожарное ведро и знаем, как нечеткие

величины можно обрабатывать четкими методами (см. рис. 6.41-6.45). Открытость программ очень важна в среде Mathcad, так как этот пакет интенсивно используется в сфере образования. Все три параметра (и еще какие-то другие) можно объединить в один интегральный и применить к нему метод экспертных оценок с функциями принадлежности какого-либо элемента (параметра) нечеткому множеству «оптимально-неоптимально».

Все три вышеотмеченные качества взаимосвязаны. Только в очень неряшливо написанной программе все параметры можно улучшить. Обычно же бывает так, что, улучшая читабельность программы человеком, мы ухудшаем ее «читабельность» компьютером: комментарии в программе (в нашем случае – текстовые константы) не только увеличивают объем программы, но и замедляют ее прогонку.

Вот другой пример. Если в программе на рис. 4.10 (сплайн-интерполяция) исходные векторы и матрицы термодинамических параметров водяного пара переместить в файл на диске, а в программе оставить операторы его считывания (функция READ), то объем программы существенно уменьшится, но читабельность ее при этом ухудшится (самое интересное уйдет с экрана дисплея), а время ее выполнения изменится.

Mathcad не имеет специализированных средств, предназначенных для оптимизации программ. В «настоящих» языках программирования, вернее, в «настоящих» средах создания программ они есть.
Одно из них, называемое «profiler» (профайлер, профилировщик), позволяет провести некий хронометраж программы и выявить ее слабые места, нуждающееся в «укреплении» (в оптимизации).
Итак, поговорим о том, как Mathcad-программы можно оптимизировать.
1. Отлаживать
программу можно только после ее написания, но оптимизировать программу не просто можно, но и нужно еще до открытия панели инструментов программирования (см. рис. 6.2). «Нет ничего практичнее хорошей теории!» – вот еще строка, заслуживающая быть плакатом (см. выше). Эта истина заставляет программиста искать для программы оптимальный алгоритм.
Как можно найти корень алгебраического уравнения на отрезке неопределенности a-b? Во-первых, можно разбить интервал a-b на небольшие отрезки, равные TOL (предопределенная переменная Mathcad, отвечающая за точность расчетов), и зафиксировать место, где значения функции ближе всего к засечкам на оси х – см. рис. 6.54.

---

---