Векторное поле (Vector Field Plot – продолжение рис. 1.20)

Вместо линий графика на рис. 1.22 можно поставить маленькие стрелочки, отмечающие направление изменения функции двух переменных. Тогда получится векторное поле (

– Vector Field Plot – рис. 1.23). Возвращаясь к географической карте, можно сказать, что маленькие векторы отмечают направления течения рек и ручьев[23]. Этот график очень полезен, например, при решении дифференциальных уравнений (см. этюд 5) – с его помощью довольно просто нарисовать семейство кривых – решений уравнения.

Трехмерный точечный график (3D Scatter Plot)

Гибридом декартова графика (рис. 1.17 и 1.18) и графика поверхности (рис. 1.21) является так называемый трехмерный точечный график (

– 3D Scatter Plot – рис. 1.24). Его главное отличие от графиков, отображающих прямоугольные матрицы (рис. 1.21-1.23), состоит в том, что с его помощью можно изобразить пространственную взаимосвязь не двух, а трех векторов (x, y и P, например). С помощью трехмерного точечного графика можно визуализировать и матрицу.

Трехмерная столбчатая диаграмма (3D Bar Chart)

Элементы матрицы (или вектора) можно уподобить столбикам, расставить их на плоской поверхности двух аргументов и получить трехмерную столбчатую диаграмму (

– 3D Bar Chart). На рис. 1.25 аргумент один. Подобный, но плоский график можно построить и в декартовых координатах (см. рис. 5.1).

О графических возможностях пакета Mathcad можно написать целую книгу (что входит в перспективные планы автора). Мы же отсылаем читателя к приложению 1, где перечислены некоторые команды настройки графиков. Видов графиков, как уже было отмечено, семь, а инструментов работы с ними – три. Первый инструмент – это форматирование графика. Объемные графики (вернее, псевдообъемные – видимость объема имитируется на все том же плоском дисплее) – это скорее способ украшения

документов, а не средство научного анализа. Настоящая работа ведется с плоскими (двухмерными) графиками. Для них в среде Mathcad припасены два других инструмента: лупа (Zoom – рис. 1.26) и трассировка (Trace – рис. 1.27).

Лупа (Zoom) графиков

Если человеку необходимо более подробно рассмотреть какой-либо объект, он берет в руки лупу ¾ она и изображена на одной из кнопок панели Graph (см. рис. 1.26). Нажав на эту кнопку, пользователь вызывает диалоговое окно X-Y Zoom с четырьмя полями и пятью кнопками. Протяжкой на рассматриваемом графике можно выделить прямоугольную область (см. рис. 1.26), отмеченную пунктиром. Координаты области отображаются в диалоговом окне X-Y Zoom. Нажатием кнопки Zoom эту выделенную область можно увеличить до размеров исходного графика ¾ и таким образом под лупой рассмотреть левый корень системы уравнений, решаемой на рис. 1.8. Можно все вернуть в исходное положение (кнопка Unzoom), выбрать новую область и раскрыть ее окончательно (Full View).

Трассировка (Trace) графиков

На график можно посмотреть как бы через прицел снайперской винтовки, если нажать на последнюю, девятую кнопку графической панели (рис. 1.27), появится диалоговое окно X-Y Trace. Если после этого курсором мыши прощупывать кривую на графике, то появятся два волоска (crosshair), координаты пересечения которых отображаются в окне Trace. Эти координаты можно скопировать (CopyX и CopyY) в буфер обмена, а потом перенести в Mathcad-документ и использовать в качестве первого приближения при поиске корня системы уравнений.

Естественно, семь графиков далеко не всегда могут удовлетворить потребности и фантазию пользователя. Разработчики Mathcad не стали утяжелять пакет «экзотической» графикой, а создали новый пакет Axum, предназначенный для более тонкой и изощренной визуализации данных из среды Mathcad. Кроме того, данные из Mathcad-документа с помощью инструмента MathConnex (см. приложение 7) можно перенести в среду Excel или MatLab и там воспользоваться графическими возможностями этих пакетов.

Мастер функций Mathcad

Встроенные операторы вводятся через нажатие кнопок с их изображением – см. рис. 1.3.

Функции (встроенные и пользовательские) с одним или двумя аргументами можно вводить в Mathcad-документ через нажатие кнопок «fx», «xf», «xfy» и «xfy» (нижний ряд на панели Evaluation на рис. 1.3). При этом появляются заготовки постфиксного

и префиксного операторов с одним операндом («fx» и «xf» – первый из них и был задействован на рис. 1.16), инфиксного «xfy» и древовидного «xfy» операторов с двумя операндами. Древовидный вызов оператора хорошо проиллюстрирован на рис. 3.14 в этюде 3.

Встроенные операторы отличаются от встроенных функций (не только в среде Mathcad, но и в программировании), во-первых, тем, что функции все равны между собой, оператор же умножения «главнее» оператора сложения: 2+2*2 равно шести, а не восьми. Кроме того, в среде Mathcad встроенную функцию с одним или двумя аргументами можно непосредственно вызвать в виде оператора (a sin, например). Со встроенными операторами не все так просто. На рис 1.29 даны иллюстрации работы функций и операторов в среде Mathcad.

Операторы и функции

Второе отличие функции от оператора в среде Mathcad в том, что оператор имеет фиксированное количество операндов: один (n! – факториал, например), два (сложение, вычитание, степень, дифференциал, неопределенный интеграл), три (сумма и произведение элементов вектора, производная высокого порядка и др.), четыре (сумма и произведение ряда, определенный интеграл (см. выше) и т.д.).

Некоторые же функции (Find, MinErr, Minimize, Maximize, например) способны иметь дело с переменным числом аргументов. Третье отличие функции от оператора в среде Mathcad в том, что встроенную функцию можно переопределить. Если, например, пользователя не устраивает то, что аргумент синуса должен быть в радианах, он может заставить синус «глотать» угловые градусы (рис. 1.29).

Внешне для пользователя функция отличается от оператора тем, что у функции есть имя (это обычно слово или сокращение слова), а у оператора – символ. Правда, некоторые операторы вообще не имеют ни имени, ни символа: xy (x в степени y) и Vi (i-й элемент вектора V). Функций-анонимов в среде Mathcad нет.

Пара операторов Mathcad может иметь один и тот же символ, но прописанный разным стилем: сравните светлое равно (вывод числового значения) и полужирное равно (булево равенство). В среде Mathcad можно оперировать одноименными переменными и функциями пользователя с различным шрифтом, с помощью которого отмечаются совершенно различные переменные и функции. Так, в расчете основные переменные можно прописать шрифтом размером 14, а вспомогательные – 10. Традиционные языки программирования такого «безобразия» не допускают.

Одна из причин популярности Mathcad заключается в том, что пользователь вправе вставлять в документы либо функцию, либо оператор в зависимости от того, к чему он привык, изучая математику в школе или в институте. Благодаря этому Mathcad-документ максимально похож на лист с математическими выкладками, написанными от руки или созданными в среде какого-либо текстового процессора (Scientific Word, ChiWriter и др.).

А вот вторая причина успеха. Традиционное программирование разводит во времени процесс решения задачи на три независимых этапа: программа пишется, затем отлаживается

и оптимизируется. В среде Mathcad эти процессы слиты воедино: вводя новую формулу в документ, можно не только посмотреть результат вычислений по ней, но и построить график, создать анимационный клип и т.д.

В среде Mathcad 7 и 8 операторы «:=» (ввод значения) и «=» (вывод значения) несколько перепутались. Если пользователь забудет, что переменная А, например, не определена, и наберет на клавиатуре «A=», то оператор вывода «=» автоматически превратится в оператор присваивания «:=» (технология SmartOperator – сообразительный оператор). Вот хорошее правило: никогда не используйте оператор «:=» для ввода значения переменной. Для этого нужно использовать оператор «=». Это убережет от случайного переопределения «занятой» переменной – как пользовательской, так и встроенной. Переменная А, например, – это один ампер.

Создавая пользовательский оператор, ему можно давать не только имя, но и символ, незанятый встроенными операторами. В конце рис. 1.29 показана технология создания булевого оператора «примерно равно», доводящего до семи (опять семь!) список операторов сравнения вещественных величин («равно», «неравно», «больше», «меньше», «больше или равно» и «меньше или равно» – см. соответствующие кнопки на панели Evaluation на рис. 1.3 и 1.29). Символ «»» берется из таблицы символов Windows (Alt+0196) или из таблицы символов самого Mathcad (см. ниже), которая вызывается из Центра Ресурсов. Здесь это уже не общая переменная (с шрифтом Arial Cyr), а переменная первого пользователя (User1 со шрифтом Symbol). На рис. 1.15 по такой же технологии введена пользовательская единица измерений – угловой градус (°).



Кроме того, диалог пользователя с компьютером в средах Mathcad 7 и 8 обогащен текстовыми переменными. Для их поддержки введены «текстовые» функции. Их работа показана в пункте 1 на рис. 1.30.

Работа текстовых функций

Между числовыми и текстовыми переменными нет глубокого водораздела. Это проиллюстрировано в пункте 2 на рис. 1.30, где моделируется бросание монетки: орел – это 1, а решка – это решка. Переменная a принимает то числовое, то текстовое значение. Об этом мы еще поговорим в этюде 6 (рис. 6.46 и 6.47). В связи с этим в среду Mathcad 8 введены специальные булевы функции, возвращающие 0 или 1 – в зависимости от типа аргумента (см. пункт 4 на рис. 1.30).

[1] Покойная матушка автора умела вычислять на счетах квадратный корень.

[2]

На рисунках книги шрифт переменных и констант Arial Cyr (см. рис. 1.29), а шрифт комментариев – Times New Roman Cyr.

[3]

Там может быть и оператор, например Vi или M<n>, локализующий элемент массива (V) или матрица (M), куда заносится соответствующее значение.

[4]

Проблему русских имен переменных в среде Mathcad мы рассмотрим в главе 6 при раскладке пасьянса.

[5]

Между Given и Find могут быть записаны и неравенства. Но об этом позже.

[6]

Элементом вектора (матрицы) может быть новый вектор (матрица). В этом случае говорят о вложенном массиве (nested arrays).

[7] В математике принято говорить «элемент матрицы» и «компонента вектора», а не «элемент вектора». Но мы будем применять второй термин, так как в среде Mathcad нет принципиальной разницы между вектором и матрицей: вектор ¾ это матрица с одним столбцом.

[8]

Если при создании матрицы нажимать не OK, а Insert, то окно работы с матрицами будет оставаться на экране дисплея.

[9] В разработке функций, предназначенных для решения алгебраических уравнений и систем (Find, MinErr и др.) принимала участие и фирма Frontline System, Inc. (см. конец приложения 1 с указанием авторских прав). Эта же фирма поставила Решатель (Solver) для электронных таблиц Excel.

[10]

Это не совсем так, вернее совсем не так – см. начало этюда 3.

[11]

Символьная математика Mathcad умеет не только выяснять, является ли выражение полиномом или нет, но и вычисляет коэффициенты полинома (см. этюд 7).

[12] В Mathcad- документ греческие буквы вставляются нажатием кнопок специальной панели (ab – см. рис. 1.3). Другой способ ввода греческих букв – аккорды: Ctrl + p дает ? и т.д.

[13] В шестой версии Mathcad в меню File появилась команда Export Worksheet, существенно облегчающая эту работу. В седьмой и восьмой версиях этой функцией нагружена команда Save as... Кроме того, Mathcad-документ можно внедрить в Word-документ (и наоборот), используя технологию OLE. В среде Word, например, можно проверить орфографию и грамматику ремарок.

[14] В среде Mathcad 7 и 8 Pro допустимы не только числовые, но и текстовые переменные.

[15] А спрашивается, чего мучились ¾ инфляция опять ставит все на свои места. Кроме того, в 1999 году появилась новая «головная боль» ¾ евро.

[16] См. информацию в конце книги (рекламная пауза).

[17] Произведение силы на длину плеча приложения.

[18] В среде Mathcad 8 уже две системные переменные, влияющие на точность расчета: привычная TOL и новая CTOL.

[19] Гражданская война в Швейцарии в 1847 г. разгорелась на религиозно-метрической почве. Семь кантонов (Зондербунд) боролись за свои собственные меры веса и длины. Кроме того, туда подмешался давний спор католиков с протестантами. Нельзя же, в самом деле, лить кровь только из-за «футов-метров». Религиозные войны – это войны за освобождение совести человека. Наша православная церковь все еще ждет своего Цвингли, Кальвина, Лютера…

[20] Вернее, зачаток вектора ¾ переменная области (Range Variable).

[21]

По умолчанию задается не шаг, как на языке BASIC, а второе значение вектора. В нашем случае они совпадают.

[22] Читатель может сделать это вручную по технологии книжек «Раскрась сам».

[23] Это не совсем так, но уж больно удачно сравнение с ручьями и реками.

[24] Расхождение можно наблюдать в трактовке даже самых простых понятий. Так упоминавшиеся нами углы, которым соотносятся значения синуса, с точки зрения математика – это множество с бесконечным числом элементов. Для программистов же углы – это множество с сугубо конечным числом элементов. Если точность – одна десятая углового градуса (обычная точность технических расчетов), то множество углов в круге имеет всего лишь 3600 элементов. Реальное число в математике и реальное число конкретного языка программирования (тип real в языке Pascal или тип Single в языке BASIC)– это, как говорится, две большие разницы. Эта тенденция хорошо описана в книге Дж. Кемени, Дж. Снелла и Дж. Томпсона «Введение в конечную математику» (Издательство Иностранной литературы, 1963). Дж. Кемени, кстати, является одним из создателей языка BASIC.

Задача о пожарном ведре: схема решения

Требуется найти угол вырезки a (альфа), при котором объем ведра будет максимальным.

Эту оптимизационную задачу можно решить аналитически: см. пункт 3.3 на рис. 2.1. Но, как понимает читатель, далеко не всякую математическую задачу можно решить аналитически. Иначе бы не было таких научных дисциплин, как «Прикладная математика», «Программирование», «Численные методы» и др. Поэтому мы рассмотрим численное

решение задачи.

И при численном, и при аналитическом решении задачи мы должны вывести зависимость объема ведра V от угла вырезки a. Далее при аналитическом решении можно взять первую производную от этой функции, приравнять ее к нулю и найти корень полученного уравнения. Не обойтись тут и без второй производной, если нужно убедиться, что найденное решение – максимум, а не минимум или точка перегиба, где, как помнит читатель из курса матанализа, первая производная также равна нулю. Жестянщик, которому поручат сделать пожарное ведро, скорее всего, незнаком с дифференциальным счислением, азы которого мы только что изложили. Но в среде Mathcad поставленная задача вполне окажется по плечу «компьютеризированному» жестянщику.

Рисунок заготовки ведра и самого ведра в пункте 1 на рис. 2.1

сделан с помощью графического редактора Paintbrush и перенесен в Mathcad-документ через буфер обмена Clipboard.

В пункт 2 на рис. 2.1 скопированы данные о геометрии конуса из стандартного справочника Mathcad, который удобен тем, что входит в состав пакета и всегда находится под рукой. Справочник открывается командой Open Book… в меню Help. Перенос данных из справочника в Mathcad-документ также автоматизирован, что исключает их искажение – списывая формулу из книги немудрено и ошибиться.

Пункт 3 на рис. 2.1 – это «воспоминание о будущем». Там записаны операторы символьных (аналитических) преобразований (см. этюд 7). В пункте 3.1 оператором solve решается алгебраическое уравнение, позволяющее сформулировать функции пользователя с именами r, h и V (см. пункт 3.2). Зависимости выводятся из несложной геометрии круга и конуса: длина дуги выкройки (2×p×R-2×p×R×a/360) становится длиной окружности в основании конуса (2×p×r), а высота конуса h, радиус его основания r и радиус заготовки R ¾ это стороны прямоугольного треугольника, длины которых связаны теоремой Пифагора (см. пункт 3.2 на рис. 2.1). Оператор substitude позволяет заменять в выражениях подвыражение на другое и вывести еще одну формулу V(a) без вызова вспомогательных функций r(a) и h(a) – см. конец пункта 3.2 на рис. 2.1.

В пункте 3.3 берется производная от V(a), которая сразу упрощается (оператором символьного преобразования simplify). Несложный анализ вида производной показывает, что оптимальный угол вырезки – это один из корней квадратного уравнения a2-720a+43200. Но мы пока на это не обращаем внимания и начинаем численное решение задачи.

Решение задачи о пожарном ведре

Пусть радиус заготовки R равен одному метру (см. начало рис. 2.2). Это можно было бы и не оговаривать[1], так как значение оптимального угла вырезки не зависит от радиуса заготовки (см. конец рис. 2.1), но для численного

решения задачи о пожарном ведре это необходимо. Правда, можно было написать проще – R:=1, не привязываясь к метрам (литрам, галлонам – см. ниже). Но единицы физических величин позволяют нам дополнительно вести контроль правильности формул через соответствие размерностей[2].

Далее записана (вернее, скопирована из рис. 2.1) цепочка функций пользователя, формирующая нашу анализируемую функцию V(a), в которую вложены другие функции – r(a) и h(a). В последнюю в свою очередь также вложена функция r(a). Механизм вложения функций и операторов (встроенных и пользовательских) ¾ это мощный инструмент не только Mathcad, но и других программных сред, позволяющий быстро и изящно решать довольно сложные задач. Вложенные функции просты по виду, а механизм их формирования открыт, чего не скажешь о функции V(a) в пункте 3.2 на рис. 2.1.

Прежде чем искать максимум функции, необходимо убедиться, что он есть. Лучший же способ увидеть максимум – просмотреть график функции. В среде Mathcad есть семь видов графиков (см. этюд 1), первый из которых (X-Y-график в декартовых координатах) отображен на рис. 2.2. Здесь график построен по «двухшаговой» технологии: задается вид функции и сразу отдается команда на вставку графика в Mathcad-документ. По умолчанию аргумент меняется от минус 10 до плюс 10 с пятьюдесятью точками на графике. После построения наброска графика его нужно будет отформатировать – изменить разброс аргумента и др.

На графике в районе 60-70 градусов отчетливо виден максимум функции. Как его уточнить?

Для решения такой задачи в Mathcad 8 встроена новая функция Maximize, возвращающая координаты максимума анализируемой функции вблизи точки начального приближения. Если из заготовки вырезать сектор с углом в 66 с чем-то градусов, то такое ведро будет иметь максимальную вместимость ¾ 403 литра (106 с половиной американских или 88 с половиной британских галлонов – продолжение темы единиц измерения физических величин, начатой в этюде 1).

Заканчивается численное решение задачи о пожарном ведре проверкой правильности решения: Доверяй, но проверяй! Для этого, во-первых, оно сравнивается с аналитическим (абсолютно точным, скопированным из рис. 2.1). Во-вторых, построен график той же функции, но на ином интервале значений аргумента – вблизи найденной точки максимума: в интервале 65-67 градусов с шагом 0.1[3]. Уточняющий график построен уже по «трехшаговой» технологии ¾ с заданием области значений переменной-аргумента a. На это приходится идти, так как переменная a к этому моменту уже имеет скалярное значение, которое мешает строить график в два шага.
На рис. 2.2 читатель может видеть переменную с индексом a опт. Но здесь индекс опт (оптимальное) не числовой, как на рис. 1.6 и 1.7, а текстовый. Числовой индекс должен иметь определенное целочисленное значение, отмечающее место переменной в векторе или в матрице. Текстовый же индекс – это всего лишь продолжение имени переменной (функции). Он вводится в Mathcad-документ для эстетического эффекта – чтобы переменные были более наглядными. Получается текстовый индекс после того, как в середину имени переменной поставят точку: было a.опт, стало a опт. Числовой же индекс, как помнит читатель, вводится либо через квадратную скобку (X[n – Xn), либо через специальную кнопку Xn панели инструментов Matrix.
Попробуем усложнить задачу о пожарном ведре. Что если вырезанный из заготовки сектор не выбрасывать, а скручивать из него второе коническое ведро? Вместимость двух ведер, естественно, будет больше вместимости одного ведра. Вопрос на пари: как необходимо раскроить заготовку, чтобы суммарный объем двух ведер был максимальным? Большинство опрошенных, опираясь на здравый смысл, ответят, что заготовку нужно разрезать пополам по диаметру, и... проиграют пари.

Решение задачи о двух пожарных ведрах

На рис. 2.3 показано численное решение «двухведерной задачи» в среде Mathcad. В основном оно повторяет решение, показанное на рис. 2.2, но имеет такие особенности:

Сделано допущение, что радиус заготовки равен единице – переменная R в расчете отсутствует.

Функция объема ведра не опирается на вложенные функции. Это несколько усложняет понимание сути задачи, но ускоряет расчет.

Объем второго ведра рассчитывается также через функцию V, но аргумент a при этом сдвинут на 360 градусов: второму ведру достаются обрезки от первого ведра.

На первом графике выведена не одна кривая, а три: объем первого ведра V(a), объем второго ведра V(360 - a) и сумма объемов обоих ведер SV(a)[4]. Кроме того, шкала оси функции начата не с нуля, а со значения 0.38 для того, чтобы пользователь отчетливо увидел два максимума у функции SV и выиграл пари: заготовку нужно разрезать не по диаметру, а несколько иначе, чтобы получить два разных ведра, но с максимальным суммарным объемом.

Построен график производной функции SV, на котором видны три точки пересечения кривой с осью абсцисс, свидетельствующих о двух симметричных максимумах и об одном локальном минимуме в середине. При форматировании первый график был обрамлен (умолчание), а на втором прорисованы оси X и Y. Второй график строится намного дольше первого из-за того, что значение производной в каждой точке графика приходится высчитывать, используя алгоритм численного дифференцирования. А это сама по себе довольно сложная задача. Можно, конечно, из рис. 2.1 скопировать в рис. 2.2 выражение для производной и работать уже с ней, но мы договорились решить задачу только численными методами.

Максимумы для разнообразия найдены не через функцию Maximize, как на рис. 2.2, а через поиск корней производной функции SV. Для этого в расчет включена встроенная функция root, возвращающая корень уравнения и тоже требующая первого приближения к решению. Изменили первое приближение с 120 на 240 угловых градусов ¾ и ответ иной (второй). Кроме того, пришлось изменить c 10-3 на 10-6

значение системной переменной TOL, отвечающей за точность нахождения корня: наша производная вблизи максимумов и минимума меняется очень слабо – в пределах 10-4.
Пожарное ведро делается в виде конуса для того, чтобы его нельзя было поставить на пол, а потом использовать не по прямому назначению (для стирки, например) – такое ведро свалится на бок[5]. Решение задачи о двух пожарных ведрах также «валится на бок» – на «левый» (a < 180) или на «правый» (a >180). Такую же форму (конус без ножки) имеет бокал типа «Пей до дна!».
Не выбросив меньший сектор и сделав из него второе пожарное ведро, мы мало что выиграли – второе ведро дало небольшую прибавку в объеме (~ 50 литров). Раскрой заготовки для двух ведер не по диаметру (a=180), а хитрым способом дал совсем ничтожный выигрыш по суммарному объему ведер (что-то около литра). Но нам важен не результат, а сам процесс расчета: «Цель ничто, движение – все!»
Теперь решим задачу, подобную задаче о пожарном ведре, но более простую и более известную – задачу о максимальном объеме коробки (см. рис. 2.4). Она тоже будет иметь интересное продолжение, связанное с утилизацией отходов.

Решение задачи о коробке

У квадратной жестянки по углам вырезаются четыре квадрата. Полученная таким образом крестообразная заготовка сгибается по пунктиру в прямоугольную призму без верхней крышки, а четыре шва свариваются (паяются). Требуется рассчитать размер сторон вырезаемых квадратов (a ¾ отношение размеров квадратов), при котором объем нашего «квадратного ведра» (коробки) будет максимальным.

На рис. 2.4 показано численное решение задачи. Оно отличается от решения по пожарному ведру (см. рис. 2.2) только видом анализируемой функции и методом оптимизации: использована функция MinErr[6] в паре с ключевым словом Given, между которыми булево равенство и ограничение, заставляющее систему искать локальный, а не глобальный максимум.

Несложный анализ функции V(a) показывает, что она имеет максимум при a=1/6. Это позволяет оценить точность использованного нами метода численной оптимизации.

Продолжение задачи о коробке также похоже на продолжение задачи о пожарном ведре: обрезки идут на изготовление новых четырех коробок, новые обрезки (их уже будет 16) тоже пойдут в дело, и так до бесконечности. Но до нее (до бесконечности) мы доберемся только в этюде 7, сейчас же рассмотрим только первые семь шагов раскроя квадратной заготовки, приводящих к формированию 5461 (1+4+16+43+44+45+46) коробок-«матрешек» (рис. 2.5).

определяющую объем плодящихся вышеописанным способом

Формулу, определяющую объем плодящихся вышеописанным способом коробок, вывести несложно[7]. Если допустить, что величина a (отношение размера вырезки к размеру заготовки) сохраняется по шагам раскроя, легко показать, что сторона исходного квадрата равна a0, четырех новых – a1, шестнадцати последующих – a2 и т.д.
Теперь спрашивается (еще одно пари!), как нужно кроить заготовки: чему должно быть равно значение a, чтобы суммарный объем коробок был максимальным?
Ответ, лежащий на поверхности, – пропорция выкройки a должна быть такой, какой она была для одной коробки (одна шестая – см. рис. 2.4). Если одна коробка имеет максимальный объем, то его будут иметь и несколько коробок! Но это не так – оптимальная точка смещается вправо по оси аргументов по мере выполнения все новых и новых шагов раскроя. На рис. 2.5 для сравнения выведены две кривые: зависимость от значения a объема одной коробки и объема 5461 коробки. Прирост объема ничтожный, но нам опять же важен не результат, а процесс расчета. Особенно наглядно это видно на рис. 2.6, где приведена формула расчета суммарного объема коробок в зависимости от пропорции выкройки a и от числа шагов раскроя n.

величина a) является функцией числа

В задаче на рис. 2.6 оптимальный размер раскроя ( величина a) является функцией числа шагов, что позволяет протабулировать аргумент и функцию и проследить дрейф оптимума и прирост суммарного объема ведер. Как видно из таблиц[8], где-то в районе 7-8 шагов раскроя точность Mathcad становится недостаточной: ответы по переменной a начинают изменяться непредсказуемо, а по V – совсем не изменяются.
При поиске оптимального раскроя коробок (рис. 2.5 и 2.6) мы предположили, что величина a, при которой суммарный объем коробок максимален, должна быть одной и той же и для больших, и для маленьких коробок. Тем самым мы свели задачу к оптимизации функции одной переменной (одномерная
оптимизация). На рис. 2.7 это ограничение снято.

суммарный объем коробок рассчитывается

На рис. 2. 7 суммарный объем коробок рассчитывается как функция уже не одного, а нескольких аргументов: первый шаг раскроя – один аргумент (пункт 1), второй шаг – два аргумента (пункт 2), третий шаг – три аргумента и т.д. В пункте 1 рис. 2.7 для сравнения использованы три допустимых в Mathcad способа поиска максимума и рассчитаны отклонения от аналитического решения при проектировании одной коробки. В пункте 2 рис. 2.7 найдены оптимальные значения переменных a и b (пропорции выкройки большого квадрата и четырех маленьких квадратиков соответственно), при которых объем пяти коробок будет максимальным (двухмерная оптимизация). Мы забыли наложить ограничения на переменные a и b в блоке Given-MinErr и второй результат оказался неверным. В пункте 3 найденный оптимум проверяется на двух графиках – на линиях уровня и на поверхности.
В среде Mathcad 8 операторы, которые разработчик документа по каким-то причинам не хочет показывать другим людям, можно оконтурить сверху и снизу границами области (команда Area в меню Insert), которую затем можно захлопнуть (команда Area-Collapse в меню Format). Это нами и сделано в пункте 3 на рис. 2.7 – там запрятаны (см. след в виде горизонтальной линии) рутинные операторы формирования матрицы M, по элементам которой строятся трехмерные графики. Если теперь по этой линии два раза щелкнуть левой кнопкой мыши (или щелкнуть раз и отдать команду Area-Expand в меню Format), то область распахнется и покажет свое содержимое:

В предыдущих версиях Mathcad операторы прятали от посторонних взглядов, помещая их за правую кромку экрана дисплея, полагая, что никто не догадается туда заглянуть (тайна Полишинеля – мы уже упоминали об этом в этюде 1).
Выделенную область можно защитить[9]
(с паролем или без оного) от редактирования (команда Area-Lock в меню Format).

Прием очень удобный. Во-первых, операторы можно прятать от самого себя – отладил какой-то участок Mathcad-документа и запрятал его от греха подальше. Другой случай. Разработчик сдал заказчику расчет, оставив на виду только зону ввода исходных данных и зону с результатом (если вернуться к рис. 1.5 с задачей о купце и сукне, то это самые нижние операторы). Остальное (что заказчику знать не следует – сам расчет) скрыто и защищено паролем. Может быть, там всего лишь пара операторов, но не простых, а гениальных. Рассказывают, что один американец починил за 1000 долларов дорогую паровую машину, стукнув по ней разок молотком. Когда ему сказали, что такая работа стоит от силы доллар, то он не стал спорить: «Да, но знание места, куда нужно бить молотком, стоит 999 долларов!»


Заканчивается рис. 2. 7 формулой, по которой можно рассчитать суммарный объем любого числа коробок, изготовленных по методике, показанной на рис. 2.5. Найдены параметры раскроя при семи шагах. У нас получилась схема оптимизации по переменному
числу аргументов. Стоит только изменить длину вектора a, тут же изменится число шагов раскроя квадратной заготовки.
Продолжение и конец решения задачи о коробках – в этюде 7, где к численным методам расчета добавятся аналитические (символьные) методы и... интеллект пользователя.
Попробуем еще немного «погреметь пожарными ведрами» и зададимся новым вопросом. Что если круглую заготовку посекторно раскроить для изготовления не одного (см. рис. 2.2) и не двух (см. рис. 2.3), а трех ведер? Сможем ли мы еще что-то «выжать» из задачи? Можно ли так раскроить круглую заготовку на три сектора и свернуть из них три конуса, чтобы превысить «двухведерный» рекорд, зафиксированный на рис. 2.3? Новая, «трехведерная» задача сводится к поиску максимума функции двух переменных: a (угол заготовки для первого ведра) и b (для второго). Третьему ведру перепадут остатки: 360-a-b.

Решение задачи о трех пожарных ведрах (начало) (середина) (конец)

На рис. 2.8 помещен протокол решения «трехведерной» задачи. Поиск максимума начат опять же с формирования функции пользователя и с ее графического анализа. Поверхность функции двух переменных строилась так, как показано в пункте 3 на рис. 2.8. Создается сетка с 1681 узлом: 41 линия (0 до 40) по оси переменной a и столько же по оси переменной b. Эта сетка кладется на плоскость a-b, а затем ее узлы (от 0 до 360 градусов с шагом 9 градусов) поднимаются по оси функции V на «подобающую» каждому узлу высоту. Далее эта ажурная конструкция с помощью диалогового окна форматирования поворачивается[10]

вокруг осей V, a и b так, чтобы человек смог увидеть то, что ему нужно, – максимумы, минимумы и др. Всю эту работу машина берет на себя. От человека требуется только наметить узлы сетки (i := 0.. 40, j := 0.. 40), дать «угловое» значение ее узлам (ai := 9×i, bj

:= 9×j – углы меняются от 0 до 360 с шагом 9), заполнить матрицу M значениями «трехведерной» функции ¾ Mi,j:= V(ai, bj), перевести курсор на свободное место и отдать команду построения трехмерного графика, отображающего элементы матрицы М.

Основной недостаток трехмерной графики Mathcad заключается в том, что область изменения аргументов должна быть прямоугольной. Но в нашей «трехведерной» задаче она треугольная, так как аргументы связаны ограничением a+b£360. В пункте 2 рис. 2.8 функция V строится так, чтобы ее значения, выходящие за рамки треугольника, приравнивались к нулю (метод штрафных санкций[11]). Из-за этого задняя грань поверхности на рис. 2.8 получилась зубчатой. Тем не менее видны максимумы на сторонах треугольника области существования аргументов a и b и провисание в центре. В трех вертикальных сечениях просматривается «двухведерный» верхний график из рис. 2.3. Пакет Mathcad не смог решить двухмерную «трехведерную» оптимизационную задачу по методике, представленной на рис. 2.3 (взятие частных производных по переменным a и b и поиск корней полученной системы алгебраических уравнений). Пакет Mathcad пытался искать максимум «у края обрыва» и «сваливался» в него. Не справилась с этой задачей и специально введенная в Mathcad 8 функция Maximize при всех трех начальных приближениях (см. пункты *.1[12]): мы «танцевали» к максимуму от трех «печек» ¾ из центра треугольника (120 и 120 градусов ¾ см. пункт 4), из одного угла треугольника (0 и 0 градусов ¾ см. пункт 5) и от одной из сторон треугольника (150 и 210 градусов ¾ см. пункт 6). С поиском максимума справилась «старая добрая» функция MinErr[13] ¾ см. пункты *.2. Старая в буквальном смысле ¾ она ведет свою родословную еще с DOS-версий Mathcad и поэтому хорошо отлажена.

В пункте 7 сделан дополнительный графический анализ через линии уровня нашей «трехведерной» задачи, которая на поверку оказалась «двухведерной». Сразу виден еще один недостаток трехмерной графики Mathcad: область существования решений ¾ это равнобедренный, а не прямоугольный треугольник[14], как в пункте 7 на рис. 2.8. Оси a и b нужно размещать не под прямым углом, а под углом в 60 градусов, но Mathcad этого делать не может.
В пункте 8 сделана попытка реабилитации функции Maximize, потерпевшей полное фиаско в пункте 6. Если функция MinErr всегда должна работать в паре с ключевым словом Given, то функция Maximize ¾ может. За ключевым словом Given при необходимости пишутся ограничения, открывающие новые возможности в решении оптимизационных задач. Если из пользовательской функции убрать штрафные санкции (переопределить ее ¾ см. начало пункта 7), то функция Maximize справится с поставленной задачей (пункты 8 и 10), если… не застрянет в «седле» (пункт 9). Мы еще раз подтвердили, что третье ведро лишнее: максимумы лежат на краю обрывов – на линиях области существования «двухведерной» задачи. Максимумов шесть. К ним можно прийти, изменяя начальные приближения.
В книге мы еще не раз будем «греметь пожарными ведрами»: в этюде 6 (тестирование программы поиска оптимума функции многих переменных) и в этюде 7 (аналитическое решение задачи о ведре).
Возможность записи перед функциями Maximize и Minimize системы ограничений в виде неравенств и равенств позволяет решать в среде Mathcad новый класс оптимизационных задач. Вот две из них.

Задача о стульях

Данная задача относится к широкому классу задач под названием задачи линейного программирования: необходимо установить план (программу!) выпуска изделий (у нас это стулья), ориентируясь на целевую функцию (у нас их две ¾ общее количество и общая стоимость стульев) и принимая во внимание ограничения

(ресурсы по доскам, ткани и человеко-часам). Из рис. 2.9 видно, что можно выпускать не более 150 стульев (максимум первой целевой функции). А вот с максимизацией их общей цены не получилось: Mathcad не умеет решать задачу целочисленного линейного программирования. План выпуска стульев, максимизирующий их количество, вышел целочисленным случайно.

Транспортная задача

Спрашивается, как нужно организовать перевозки (найти значения переменных с1м1, с1м2, с2м1 и с2м2), чтобы затраты были минимальны. На рис. 2.10 дан ответ. Парадокс задачи в том, что по самому дешевому маршруту (со второго склада в первый магазин – 800 у.е.) ничего не возится (с2м1 = 0). Этот парадокс мы также обыграем в следующем этюде.

Задачи на рис. 2.9 и.2.10 простенькие, но очень, если так можно выразиться, жизненно важные. На каждом шагу приходится что-то оптимизировать (расходы, например), принимая во внимание всякого рода ограничения (доходы!). Возвращаясь к сноске 17, можно привести такой пример. После часа пик (зимнее утро, к примеру) расход электроэнергии падает и необходимо снижать нагрузку электрогенераторов. Как это делать? Можно отключить отдельные турбогенераторы, а можно оставить их в работе, изменив нагрузку. Диспетчер энергосистемы дает соответствующие команды, ориентируясь на некие целевые функции: средний расход топлива по системе, выброс с дымовыми газами вредных веществ в атмосферу, износ оборудования, степень готовности электростанций и дальше менять нагрузку и т.д. Переменные такой оптимизации могут быть и вещественными (мощность отдельного энергоблока, которая меняется, естественно, в разумных пределах, определяемых техническими условиями – ограничения в задаче) и целочисленными (число работающих блоков). Эта задача очень сложная, но и очень эффективная – здесь речь идет о высвобождаемых составах с топливом.

Вот еще примеры. Когда нужно убирать пшеницу? Пораньше – зерно еще не вызрело. Попозже – часть зерна уже осыпалась. Сколько и каких акций стоит купить на ограниченную сумму денег, чтобы будущий дивиденд был максимален? В каких средствах массовой информации стоит размещать рекламу на выделенные по смете деньги, чтобы эффект от нее был максимален?

Разговор об оптимизации мы продолжим в этюде 3 в несколько ином ключе.

[1] Тем более что, переменная R уже занята под хранение градусов Ренкина. В этом можно убедиться, набрав R= и получив R=0.556 K (градус Ренкина в градусах Кельвина). Присвоением R:=1m мы «испортили» данную системную переменную, что может выйти нам боком, если в расчет придется вводить температуру. Отсюда вытекает хорошее правило работы в среде Mathcad: «Никогда не пользуйтесь оператором «:=». Для присваивания значения переменной лучше работать с оператором «=», автоматически превращающимся в оператор «:=», если соответствующая переменная не занята пользователем или системой.

[2] В предыдущем издании книги автор так и написал R:=1 без указания, что это не просто единица, а единица длины. Из-за этого в формуле для h была допущена, а, главное, не исправлена, ошибка, сказавшаяся бы на расчете, если бы R стала равна не единице, а, допустим, двум.

[3] Такую работу может сделать и «Лупа» графика – см. рис. 1.26.

[4] Здесь ? не символ суммы, а просто заглавная греческая буква «сигма». Три функции вводятся в график через запятую, но автоматически выстраиваются столбиком.

[5] Автор, служа в армии и моя там, как водится, полы, ставил пожарное ведро (другого не было) в перевернутую табуретку. Отсюда и «любовь» к пожарным ведрам, вылившаяся на страницы этой книги.

[6] Эту функцию мы еще помянем добрым словом ¾ см. сноску 13.

[7] В среде Mathcad допустимо разрывать длинные суммы для более компактного их размещения на экране дисплея и на бумаге принтера. Для этого нужно нажать Ctrl+Enter вместо плюса.

[8] У нас получились некие лестницы, которые мы еще обыграем, рассказывая о чувствах, которые могут охватывать пользователя Mathcad.

[9] Эта возможность появилась еще в седьмой версии Mathcad.

[10] В среде Mathcad 8 эту работу можно делать по новой технологии: прижать график левой кнопкой мыши и вращать его, двигая мышь.

[11] Функция max здесь работает в качестве логического ИЛИ – см. в этюде 3 главку «Mathcad и булевы (логические) функции»: если a<0, или b<0, или a+b>360, то объем ведра становится равным нулю, иначе – сумме объемов трех ведер.

[12] Здесь звездочка это 4, 5 и 6. Пользователям ЭВМ такое сокращение (обобщение) знакомо по работе с файлами.

[13] Библейские герои за свои заслуги перед Богом получали дополнительную гласную в свое имя: Был Аврам (Абрам), стал Авраам (Исак – Исаак и т.д.). В Mathcad 8 имя нашей «заслуженной» функции изменилось: было minerr (или Minerr), стало MinErr.

[14] Треугольник – это основа визуализации трехкомпонентных смесей

(сплавов): поверхность над таким треугольником отображает какой-либо параметр (плотность сплава, к примеру), а стороны треугольника – это процентное содержание каждого из трех компонентов. Углы треугольника – чистый металл, стороны – двухкомпонентный сплав, а нутро треугольника – трехкомпонентный сплав. Очень часто здесь, как в драке, третий оказывается лишним. Так, например, припой для пайки – это сплав свинца с оловом, имеющий минимальную (опять оптимизация) температуру плавления. Добавление в припой третьего металла (цинка, например) только ухудшает этот основной его технологический показатель.

[15] Это, естественно, не доллары США, а на самом деле условные единицы, не влияющие на решение задачи.

[16] Автор сначала хотел было написать «компьютеров», ориентируясь на тематику данной книги, но потом передумал – см. следующую сноску.

[17] Автор на своих лекциях в Московском энергетическом институте заменяет магазины на электростанции, куда из шахт

подвозится уголь. Одним словом, «Служил Гаврила почтальоном, Гаврила уголь, пардон, почту развозил…» – см. предыдущую сноску. Уголь удобен тем, что это не целочисленная задача.

Поиск корня уравнения

Теперь мы подшутим

над функцией root, и если не получим от этого удовольствия, то хотя бы уясним себе, какие «подводные камни» могут нас ожидать.

Если в качестве первого приближения (опорной точки) принять не минус 50, а плюс 5 (пункт 5), то функция root выкинет «белый флаг»: сообщение «Can’t converge to a solution», отказываясь решать поставленную задачу, хотя плюс 5 намного ближе к корню, чем минус 50. Вот вам и первое приближение! Но это еще полбеды. Настоящая беда случается тогда, когда функция root (как, впрочем, и некоторые другие функции и операторы Mathcad) не отказывается решать поставленную задачу, выдавая при этом неверный результат (феномен медвежьей услуги).

Если функцию y(x) умножить на константу, например на 10-5, то ее корни останутся на старых местах. Но это утверждение в среде Mathcad не является истиной – см. пункт 6 рис. 3.1.

Не то беда, Авдей Флюгарин,

Что родом ты не русский барин,

Что на Парнасе ты цыган...

Беда, что скучен твой роман.

Не то беда, что ты, Mathcad, неправильно решил простейшую задачу: и более мощные специализированные пакеты, ориентированные только на решение алгебраических уравнений и систем, делают тут промах. Беда в том, что Mathcad в этом честно не признался, как это было в пункте 5 на рис. 3.1.

Философский смысл любой шутки заключается в том, что у шутника и у того, над кем подшучивают, разные понятия о природе вещей. У пользователя и у среды Mathcad разные понятия о том, что такое корень уравнения: человек считает, что корень – это то значение аргумента, при котором выражение равно нулю; функция же root «считает», что корень – это то значение аргумента, при котором значение выражения по модулю не превышает значения системной переменной TOL, которая по умолчанию равна 10-3. Отсюда и путаница в пункте 6 на рис. 3.1. Чтобы функция root там сработала правильно, необходимо переменной TOL присвоить новое значение (10-7, например), заменив им предопределенное. Можно поступить и по-другому – умножить в пункте 6 правую часть функции на 100000, убрав тем самым коэффициент 0.00001. Метод балластных (нормирующих) коэффициентов особенно эффективен при решении алгебраических систем (что уже было отмечено в этюде 1). Он позволяет уравнять все уравнения (прошу простить за тавтологию) по отношению к точности, с которой система решается через блок Given-Find. На нижнем графике рисунка 3.1 ось X «утолщена» до значения TOL (пунктир). Корень там, где кривая касается этой «толстой» оси.

В среде Mathcad 8 переменная TOL была дополнена еще одной системной переменной ¾ CTOL (tolerance of the constraints ¾ точность ограничений), которая также по умолчанию равна 10-3, но уже отвечает не за поиск корней и оптимумов, а за ограничения ¾ за уравнения и неравенства, записанные после ключевого слова Given.

С промахом, зафиксированным в пункте 5 рис. 3.1, можно разобраться после знакомства с вычислительными методами, заложенными в функцию root. В Руководстве пользователя Mathcad сказано, что функция root ищет корень выражения методом секущих, и дано его описание, которое автор перевел на язык BASIC.

' Поиск корня уравнения методом секущих

' Реализация на языке BASIC Mathcad-функции root

 

Def FnY(x) = 2 * X ^ 3 + 20 * x ^ 2 – 2 * x + 100 ' Анализируемая функция

TOL = 0.001 ‘ Точность поиска корня

‘ Начало процедуры поиска корня

Input "X нач. :=", X ‘ Начальное приближение

If Abs(FnY(X)) < TOL Then

            root = X ‘ Начальное приближение и есть корень уравнения

  Else ‘ Расчет второй опорной точки

            If X = 0 Then h = TOL Else h = X * TOL

            X0 = X : X1 = X + h

            Do ‘ Цикл приближения к корню

                        root = X1 – FnY(X1) * (X1 – X0) / (FnY(X1) – FnY(X0))

                        X0 = X1: X1 = root ' Подготовка к следующему приближению

            Loop Until Abs(FnY(X1)) <= TOL ‘ Условие завершения цикла

End If

Print

"Y=0 при X="; root ‘ Вывод результата

BASIC-программа поиска корня уравнения

Проанализировав эту программу, можно понять, почему корнем другого уравнения Y = X2 - 4 при нулевом (симметричном – проблема Буриданова осла) начальном приближении оказывается плюс, а не минус 2:

x := 0          x := root(X2 - 4, X)    x = 2

Хотя в BASIC-программе полностью реализован метод секущих, описанный в Руководстве пользователя, но...

Во-первых, в вышеприведенную BASIC-программу не заложено никаких сообщений об ошибках, а функция root его выдает (см. пункт 5 рис. 3.1). Во-вторых, BASIC-программа, в отличие от функции root, прекрасно нашла корень уравнения y(x), заданного в пункте 1, от начального приближения, равного плюс 5. И, в-третьих, в BASIC-программу заложен не метод секущих, а комбинированный метод Ньютона-секущих. Классический метод секущих требует задания не одного, а двух начальных значений аргумента: через одну точку проводится касательная (метод Ньютона), а через две – секущая. Вот так мы разобрались с функцией root! Хотели над ней подшутить, а она сама над нами посмеялась.

В этюде 6 читатель может найти функции пользователя для поиска корней уравнений методом Ньютона, методом половинного деления и методом секущих, ориентированные по точности не на значение анализируемой функции (Do ... Loop Until Abs(FnY(X1)) <= TOL – см. программу на рис. 3.2), а на значение аргумента (Do ... Loop Until Abs(X1 – X0) <= TOL, например). На такую подмену приходится идти, решая реальную задачу. Так, например, в коллекции автора есть учебная программа определения значения рН раствора, где рН ¾ это корень уравнения электронейтральности раствора (баланс катионов и анионов). Но нас мало интересует дисбаланс ионов (отклонение анализируемой функции от нуля) ¾ главное, чтобы новое значение рН отличалось от предыдущего не более чем на величину 10-3

(обычная точность рН-метра).

Поиск минимума у двухмерной экспоненциальной функции

Двухмерная экспоненциальная функция имеет минимум (нулевое значение) при x=1 и y=10. Это хорошо видно в пункте 1 на рис. 3.3, где показаны поверхность и линии уровня вблизи минимума[2]. Эти графики несложно построить, если, конечно, знаешь, где находится минимум, охватываемый переменными x1, x2, y1 и y2. Поверхность развернута так (см. ее координаты на фрагменте окна редактирования), чтобы линии уровня являлись проекцией поверхности на горизонтальную плоскость.

В пункте 2 при поиске минимума в качестве начальных приближений давались точки, расположенные по углам прямоугольника ¾ области существования аргументов на графиках. Так испытывалась сходимость метода поиска минимума. Зафиксирована всего лишь одна осечка: при начальном приближении x=1.2 и y=14 не был найден корень системы, состоящей из приравненных к нулю частных производных двухмерной экспоненциальной функции[3].

Поиск минимума у функции Розенброка

Функция Розенброка примечательна тем, что ее минимум невозможно увидеть ни на линиях уровня, ни на поверхности (пункт 1 на рис. 3.4). Скажем осторожнее – автору не удалось этого сделать. На графиках просматривается типичный овраг, где анализируемая функция в одном направлении изменяется круто, а в перпендикулярном – слабо. Этим пытаются как бы дезориентировать программу поиска минимума – на то и создаются тестовые функции. Графики строились по новой, третьей технологии ¾ задавался центр (x и y) квадрата со стороной 2D области существования аргументов на графиках. Вторая технология ¾ это когда задаются координаты углов прямоугольника существования аргументов на графиках (см. пункт 1 на рис. 3.3). Первая технология (кстати, самая неудобная для понимания) была использована, например, в рис 2.8 – там область размаха поверхности завуалирована в значениях переменных i и j.

В пункте 2 на рис. 3.4 поиск минимума велся от трех начальных точек (10-10, 100-10 и 100-100) тремя способами. Итоги «соревнования»: на первом месте по-прежнему функция MinErr, которая выдавала абсолютно точный результат (пару единиц). На втором месте функция Minimize c относительно правильными ответами. Функция же Find сошла с трети дистанции – только при первом приближении был выдан относительно точный результат. Здесь, по-видимому, с функцией Find овраг сыграл злую шутку.

Функция Розенброка имеет минимум (нуль) при x=1 и y=1. Через эту точку можно провести секущие плоскости и показать на декартовых графиках, что функция там минимальна (см. пункт 3 на рис. 3.4), ее частные производные равны нулю, а частные производные второго порядка положительны.

Поиск минимума у функции Пауэла

Функция Пауэла (рис. 3.5) имеет четыре аргумента. Следовательно, в трехмерном мире – даже виртуальном – никакими поверхностями и линиями уровня минимум (нуль) функции Пауэла не локализовать (не визуализировать). Проверить соответствие найденной точки (четыре нуля) минимуму можно либо через декартовы графики сечений по технологии рисунка 3.3), либо через линии уровня, что и было сделано в пунктах 2.1 и 2.2 на рис. 3.5. Для этого две координаты фиксируются на нулевых значениях, а две другие изменяются вокруг нуля (нули – это координаты минимума). Таких топограмм четырехмерной функции можно построить шесть штук следующих пар аргументов: a0-a1, a0-a2 (см. рис. 3.5), a0-a3, a1-a2, a1-a3 и a2-a3 (по четырем последним парам читателю предлагается построить топограммы самому). Решение по функции Пауэла более-менее удачно велось с помощью функций MinErr и Minimize. Поиск корня системы четырех алгебраических уравнений – частных производных функции Пауэла – здесь применить нельзя, так как переменные анализируемой функции у нас не скалярные величины (с именами a, b, c и d, например), а одиночная переменная-вектор с именем a. По индексным переменным производная в среде Mathcad не высчитывается. Читатель при желании может переопределить функцию Пауэла (задействовать в ней четыре переменные-скаляра) и решить задачу с помощью частных производных. Так, кстати, решалась эта задача в предыдущих изданиях книги.

Выводы по испытаниям трех функций – в конце этюда.

Подсчет числа p методом Монте-Карло

Есть более простой способ статистического расчета числа p, чем тот, который использовал Бюффон. Можно нарисовать квадрат, вписать в него круг («квадратура круга») и бросать туда камешки. Так как в площади круга запрятано число p («пи эр в квадрате» – вспомним старый анекдот о том, почему у поезда колеса стучат), то через подсчет попаданий в круг можно оценить число p. Бюффон этот метод не использовал наверное из-за того, что трудно добиться равномерного попадания камешков в квадрат.

На рис. 3.6 зафиксирована оценка площади круга, вписанного в квадрат, и сделана попытка расчета значения числа p. Как это делалось?

В пункте 1 на рис 3.6 формируются два вектора X и Y, элементы которых (а их 7000) ¾ случайные вещественные числа в интервале от минус до плюс единицы. X и Y – это по своей сути координаты точек случайного падения камешков в квадрат размером 2 на 2. Далее в пункте 2 эти камешки сортируются на «чистых и нечистых»: координаты точек, попавших в круг, дублируются в векторах Xo и Yo (o ¾ попал), а не попавших ¾ в векторах Xx и Yx (x ¾ промах). После этого несложно визуализировать попадание точек в круг с помощью параметрического декартового графика. Достаточно при форматировании графика указать, что линий нет, а есть одни точки. При этом точки, попавшие в круг (вектора Xo и Yo), более толстые. Теперь для оценки числа p можно подсчитать число попаданий камешков в круг (пункт 4) ¾ число ненулевых элементов вектора Xo (или Yo). В пункте 5 число p рассчитывается и сравнивается с его точным значением.

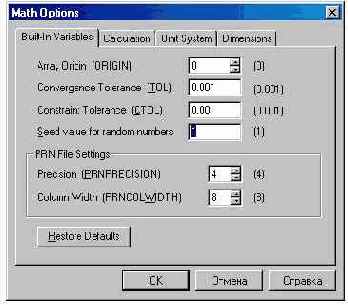
Функция rnd в среде Mathcad имеет аргумент, отличающийся от своих аналогов на языках программирования. В среде BASIC или Pascal аргумент функции rnd связан с приставкой псевдо- в ее названии, а не с диапазоном генерируемых случайных чисел. Да, числа генерируются случайные, но ряд этих чисел псевдослучаен, так как его в любой момент можно повторить. За такой повтор на языках программирования отвечает аргумент функции rnd, а в среде Mathcad – число (по умолчанию это 1), хранящееся в окне Seed value for random numbers (инициализация генератора случайных чисел) ярлыка Built-in Variables окна Math Options, которое вызывается на дисплей командой Options в меню Math:

От истинно случайных чисел отказались еще на заре развития компьютерной техники, когда пытались встраивать в ЭВМ что-то похожее на рулетку. Но это устройство оказалось слишком неповоротливым, а главное, с его помощью невозможно было получать повторяющиеся ряды случайных (псевдослучайных) чисел, что необходимо при отладке программ. Поэтому генерированию случайных чисел на физических моделях (рулетка) предпочли их математическое моделирование. Какой алгоритм заложен в функцию rnd, пользователя волнует мало – главное, чтобы ряд генерируемых чисел не вырождался, а сами числа распределялись в заданном диапазоне равномерно[4], в чем можно убедиться визуально – см. пункт 3 рис. 3.6.

Наш подсчет числа p методом Монте-Карло (а рулетка была не зря упомянута) – это чистой воды извращение (пардон, деривация): то же число p (или интеграл) легко можно рассчитать напрямую – конец пункта 5. Но все-таки наше извращение было не таким уж извращенным.

Во-первых, решив задачу на рис. 3.6, мы, по сути, не рассчитали значение p, а проверили качество генератора псевдослучайных чисел, то есть добротность встроенной функции rnd. При числе бросаний «камешков в воду», стремящемся к бесконечности, ошибка метода Монте-Карло должна стремиться к нулю, если функция rnd работает правильно.

Во-вторых, есть фигуры, площади которых невозможно рассчитать традиционными методами, без «извращений». Пример – площадь облака на снимке из космоса. Эту площадь довольно точно и, главное, быстро (в метеорологии вчерашний прогноз никому не нужен) можно определить, ткнув случайным образом несколько раз в фотографию иголкой, и… см. рис. 3.6.

Традиционные способы подсчета площади фигуры (интеграла) тут не годятся не только потому, что контуры облака невозможно описать какой-либо интегрируемой функцией, но и из-за того, что они размытые, нечеткие.

В математике, самой точной на свете науке, появилось новое направление: теория нечетких множеств (другой термин – «размытые множества», но по-английски это звучит более поэтично: «fuzzy sets» – пушистые множества[5]). Эта теория оперирует такими «перлами», как «скорее 1, чем 2», «скорее плюс, чем минус», «точка находится скорее под графиком, чем над ним» и т.д. В основе теории нечетких множеств лежит знаменитый софизм: «Если к горсти зерна добавить еще одно зернышко, превратится ли она в кучу? А если добавить два зерна? А сколько зерен превратят горсть в кучу?» Это самое сколько



– типичный представитель fuzzy set, к которому трудно приложить и современную теорию чисел, и саму цифровую вычислительную технику. Программирование же – это по своей сути жонглирование нулями и единицами, то есть крайняя категоричность мироощущения, когда все богатство цветов и оттенков сводится к черному и белому. Мир же состоит не из чисел, а из куч, горстей, облаков, то есть из нечетких множеств, к обсчету которых современные компьютеры приспособлены очень плохо. Кто поднимался на самолете сквозь облака, знает, что никакой границы между облаком и не облаком нет. В этом-то, по-видимому, и будет заключаться один из будущих кризисов теории программирования и вообще элементной базы компьютеров. К теории нечетких множеств мы еще вернемся в конце этого этюда в главке о четкой и нечеткой логике и в этюде 6. А пока задание читателю – реализовать в среде Mathcad метод подсчета числа p, предложенный Бюффоном.

Поэтому повторяю – наше извращение на рис. 3.6. было не таким уж извращенным.

Можно сказать, что на рис. 3.6. мы, подражая Казимиру Малевичу, нарисовали «Черный круг в черном квадрате». Так мы невольно вторглись в Мир Искусства…

Считается, что искусство зиждется на трех китах. Вот они: чувство меры, воображение и ... потребность в извращениях, связанная с сомнениями и творчеством.

Теперь о сомнениях.

Подсчет объема конуса

На рис. 3.7 не только рассчитан объема конуса методом Монте-Карло, но и дано изображение самого конуса. В изобразительном искусстве есть направление, называемое пуантилизм

(от французского pointiller – писать точками). Его последователи формируют картину отдельными мазками правильной точечной или прямоугольной формы. Мы уже нарисовали в такой манере «Черный круг в черном квадрате». «Натюрморт с конусом», выполненный в этом же стиле, можно увидеть в пункте 3 рис. 3.7. Здесь «поработал» Scatter Plot – трехмерный точечный график. Так незаметно мы перешли от двухмерной к трехмерной графике – от живописи к… скульптуре.

Рисовался (вернее, ваялся) конус так. В прямоугольный параллелепипед размером 2 на 2 на 1 бросались случайным образом «камешки» – формировались три вектора X, Y и Z, элементы которых – случайные числа в диапазоне минус единица – плюс единица (векторы X и Y) и ноль – единица (вектор Z см. пункт 1 на рис. 3.7). Далее точки, не вписывающиеся в конус, отсеивались: соответствующим элементам вектора Z присваивалось значение бесконечности (пункт 2), и они... «улетали на небо», формируя линию над конусом (пункт 2).

Пункты 3 и 4 – это подсчет объема конуса методом Монте-Карло и сравнение его с истинным объемом конуса[6]. Сомнения остались, но очень незначительные – в пределах ошибки метода Монте-Карло.

Один великий художник сказал, что ваять очень просто – берется глыба мрамора и от нее отсекается все лишнее. «Всякий талант неизъясним. Каким образом ваятель в куске каррарского мрамора видит сокрытого Юпитера и выводит его на свет, резцом и молотом раздробляя его оболочку?»[7]

А вот еще одно парадоксальное высказывание: «Играть на фортепиано очень просто. Достаточно в нужный момент нажимать нужные клавиши!» Все это можно рассматривать как некую браваду или как попытки Художника подурачить публику, пристающую с «глупыми» вопросами о тайне творчества. А можно принять за руководство к действию. С живописью мы разобрались (см. рис. 3.6) – возьмемся теперь за скульптуру.

На рис. 3.7 у нас есть «глыба мрамора» размером 2 на 2 на 1, от которой также отсекается лишнее (осколки падают не на пол, а улетают на небо). Пока у нас «изваялся» простой конус, но ничто не мешает нам усложнить формулы в пункте 2 на рис. 3.7 и слепить Венеру Милосскую или Мыслителя Родена… На рис. 3.8 дается методика ваяния человеческой фигуры.

Ваяние на компьютере

Автор пока поступил проще. Он через команды форматирования графика окрасил точки конуса на рис. 3.7 в зеленый цвет, подбросил еще несколько точек красного цвета и большего диаметра. Поучилась неплохая новогодняя елка.

Сейчас компьютер широко используется как рабочий инструмент художника (интеллектуальная кисть или что-то в этом роде). Распечатки цветных принтеров оправляются в рамки и выставляются в, так сказать, реальных и виртуальных компьтерно-художественных салонах (см., например, журнал «КомпьюАрт»).

Но автору хотелось бы обратить внимание уважаемых читателей на другое – на проблему эстетического вида не просто компьютерных рисунков, а листингов программ и, в частности, на проблему соответствия (или противопоставления) формы листинга содержанию программы.

Программисты, которым не чуждо образное мышление, давно уже подметили, что процедуры и функции имеют свое собственное «лицо», по которому она безошибочно узнается на экране дисплея или на бумаге принтера. Одна процедура как ухоженная крестьянская лошадка круглая и гладкая – работает себе спокойно, перекачивая, например, данные из одного формата в другой. И внешне она неприметна –  взгляд на ней не останавливается. Другая процедура все время норовит выкинуть какой-нибудь фортель, настолько она неотлаженна (необъезженна). И своими очертаниями она походит на скакуна, в седле которого сидит герой многочисленных живописных полотен и скульптур. Третья процедура так и просится, чтобы ее оправили в раму и повесили на стену, настолько она хороша и закончена, а главное, ее форма полностью отвечает ее содержанию. Она передает не только мысли, но даже и настроение

художника, пардон, программиста, ее создавшего.

Автор далеко не искусствовед и не смеет особо распространяться на эту тему.

В комментариях к публикуемым компьютерным рисункам, как правило, подчеркивается, что их авторы – компьютерные художники. В прилагательных к существительным очень часто таится некая ущербность или по, крайней мере, двусмысленность: не просто математика, а «Прикладная математика» – см. главку «Mathcad и Maple» в этюде 7. Термин компьютерный художник

содержит в себе некую двойственность. С одной стороны, прилагательным «компьютерный» как бы извиняются перед потенциальным зрителем за эстетику рисунков (см. наши «рисунки» 3.6 и 3.8). А с другой стороны – предупреждают о том, что при создании рисунков использовались специфические инструменты и методы (авангардистские изыски).

Настоящий художник готов работать на чём угодно и чем угодно. Рисунки Анатолия Зверева (художника с трагической судьбой, какая, увы, часто постигает гениев), выполненные чуть ли не окурком на обрывке листа бумаги, продаются на аукционах за большие деньги. Давайте дождемся времен, когда распечатки принтеров будут выставляться в Лувре, в Эрмитаже или на худой конец продаваться на художественных аукционах. Последнее вряд ли случится. На аукционах могут продать дискету, принадлежавшую компьютерному художнику (фетиш – сейчас так продаются гитары великих музыкантов). Дело в том, что у computer art нет понятия оригинала и копии[8]. А это может убить даже настоящие шедевры, которые иногда публикуются на обложках и внутри глянцевых изданий. Пушкин говорил: «Пóшло то, что пошлó в народ». Только самые гениальные произведения искусства способны выдержать такое испытание хождением в народ. Они-то и формируют пласт культуры, на котором базируется современная цивилизация.

Лучший способ охарактеризовать какое-либо явление – тем более в книге с претензией на искусствоведение –  это привести классическую цитату. Вот она:

Они сначала нравилися мне

Глазами синими, да белизною,

Да скромностью – а пуще новизною;

Да, слава богу, скоро догадался –

Увидел я, что с ними грех и знаться –

В них жизни нет, все куклы восковые;

А наши!...

Угадайте, о чем говорил пушкинский Дон Жуан! Да-да – и о компьютерной анимации, о рисунках, созданных с помощью компьютерной графики... Скажем мягче (и с надеждой) – о современных образцах этого симбиоза науки, технологии и искусства. Ведь, в компьютерных рисунках больше чувствуется несовершенный инструмент (новизна – парадокс high technology), чем художник.

Задача о пожарных ведрах: перебор

В решении задачи о пожарных ведрах на рис. 3.9 в пунктах 1 (одноведерная задача) и пункт 2 (двухведерная задача) формируются векторы a, V и V2 по 361 элементу в каждом[9]. Ключевой оператор решения использует встроенную функцию max, возвращающую максимальное значение своего аргумента – вектора (матрицы). Функции, возвращающей номер максимального элемента вектора (матрицы), в среде Mathcad нет – с рассуждениями по этому поводу читатель может ознакомиться в этюде 4. Поэтому на рис. 3.9 (как и на рис. 3.6 и 3.7) задействован оператор суммы, перебирающий все варианты ведер и запоминающий угол вырезки для изготовления одного ведра максимального объема – 66 градусов (пункт 1) или двух ведер с максимальным суммарным объемом – 117 и 243 (360-117) градусов (пункт 2). Наш метод перебора опасен тем, что если у вектора (матрицы) два и более максимальных значений (как у вектора V2), то в лучшем случае появится сообщение об ошибке, а в худшем – неправильный ответ (см. пункт 2 на рис. 3.9 с aопт[10]=360). При решении трехведерной задачи (пункт 3) на область максимума была как бы наброшена сетка, в узлах которой просчитаны значения «трехведерной» функции. Далее были определены координаты сетки, где данная функция максимальна. Такой контрольный расчет перебором еще раз показал, что третье ведро лишнее – мы получили уточненное решение двухведерной задачи из пункта 2.

Наше решение выглядит несколько извращенным – в функцию max, составляющую ядро расчета на рис. 3.9, и в другие, ей подобные, также заложен перебор: что-то другое здесь вряд ли придумаешь.

Хотя как сказать. Представим такую житейскую ситуацию. Садовод собрал на своем дачном участке урожай яблок и решил похвастаться самым крупном

плодом перед соседями. Будет ли он перебирать все яблоки, чтобы выбрать предмет гордости? Конечно, нет. Самое большое яблоко никому не нужно. Нас интересует самое большое яблоко с определенной степенью вероятности. Кроме того, в термин «большое» мы вкладываем не вес яблока и не его геометрические размеры, а его зрительный образ.

Пусть у нас 100 плодов. Берем первое попавшееся более-менее крупное яблоко и считаем, что оно самое большое со степенью вероятности, намного превышающей 1% (1/100). Второе выбранное яблоко (а оно, естественно, должно быть больше первого) существенно повышает вероятность выбора самого большого. Так очень скоро, перебрав (взвесив, измерив или просто оценив на глаз) всего лишь несколько яблок, а не все сто, можно выбрать относительно самое большое яблоко. Кто-то возразит, что яблоки перед отбором могут быть кем-то
отсортированы так, что самое большое окажется в хвосте очереди (на дне корзины). Но это уже будет искусственная ситуация, враждебная человеку[11]. Мы же говорим о дружественных
ситуациях. Данный алгоритм станет совсем естественным, если отбирается не самое большое, а, например, самое красивое яблоко. Здесь полный перебор будет уж совсем диким. К понятиям большое и красивое можно приложить теорию нечетких множеств, о которой речь пойдет в этюде 6.
К сожалению, задачи, приведенные в данной книге, начиная с самой простой (задача о купце и сукне – см. этюд 1) и заканчивая самой сложной (это, наверное, задача о трехсторонней дуэли – см. этюд 6), нельзя отнести к разряду естественных. Все они довольно надуманные, призванные скорее иллюстрировать возможности Mathcad, а не показывать пути решения практических задач. Автора утешает и одновременно огорчает то, что таким недостатком грешат почти все книги по программным средам. Надуманная задача – это призма, сквозь которую вдумчивый читатель посмотрит на реальную задачу.

Определение плана выпуска стульев: перебор

Оказывается, при переборе всех вариантов выпуска стульев (а их не так уж много – на рис. 3.10 мы просчитали 150 на 150 = 22 500 вариантов) можно найти два оптимальных плана, причем самый оптимальный и по цене, и по количеству (20+112=132 стула стоимостью 1504 у.е.) – это не округление дробного ответа, полученного на рис. 2.9. Возвращаясь к теме враждебности задачи, можно так подобрать ее условия, что ответ окажется совсем вдалеке от первоначального дробного…

Это был эпиграф, приступаем к рассказу.

У Михаила Жванецкого часто спрашивают, откуда он берет темы для своих миниатюр. «Выглядываю в окно и прислушиваюсь к разговорам на улице», – таков ответ великого сатирика. «А как Вы все это запоминаете?», – следует новый вопрос. «Да я забыть не могу!»

Житейские сюжеты стоит коллекционировать и для написания компьютерных этюдов, что является хобби автора этой книги.

По профессии автор – преподаватель вуза (Московского энергетического института), где он читает курс лекций по информатике и смежным дисциплинам, а также руководит группой технологов и программистов, разрабатывающих обучающие программы и компьютерные тренажеры для ТЭС и АЭС[12]. Электростанциям и энергообъединениям нужны наши программы, но их приобретению мешает пресловутый кризис неплатежей. Вот какой компьютерный этюд имел место в марте 1997 года.

Акционерное общество Тамбовэнерго, не имея свободных денег, тем не менее изъявило желание приобрести наши программы. Котовскому лакокрасочному заводу (ЛКЗ – Тамбовская обл.) для производства нужна электроэнергия. Московскому энергетическому институту для ремонта аудиторий требуется краска. Нашей научной группе необходимо новое компьютерное «железо», инструментальные средства и, естественно, зарплата. Для решения подобных проблем человечество еще на заре цивилизации придумало деньги[13]. Переход же нашей страны от непонятно чего к рынку возродил натуральный обмен – бартер[14]. В вышеописанной товарной цепочке не хватало одного звена, чтобы она замкнулась. К счастью, в МЭИ поступила партия компьютеров, парочку которых мы договорились обменять на краску. В этой комбинации заключается только часть описываемого компьютерного

этюда, если вспомнить шахматное толкование слова «этюд» – решение головоломки путем составления цепочки ходов.

Вторая часть компьютерного этюда имела место уже в Тамбове и в Котовске – на ЛКЗ. В Тамбовэнерго мне (автор переходит к рассказу от первого лица) после сдачи программ выдали доверенность на получение лакокрасочной продукции на 14 млн., естественно, старых рублей в счет задолженности завода за электроэнергию и отправили в Котовск. В отделе сбыта ЛКЗ сначала наотрез отказались отпускать краску за какие-то там непонятные задолженности, а не за живые деньги, но после угрозы отключения света и тепла с трудом, но согласились. Краска, которая мне подходила[15], вернее не мне, а отделу снабжения МЭИ, стоила 14 600 рублей за литр и разливалась в тару (в барабаны, если следовать москательному жаргону, которого я нахватался в Котовске) объемом 15 и 55 литров. Пустые барабаны стоили 24 и 30 тыс. рублей соответственно. Работница отдела сбыта ЛКЗ (ее звали Оля), выписывая на компьютере накладную, спросила, в каких емкостях (пардон, барабанах) я возьму краску. Чутье давнего собирателя компьютерных этюдов сразу подсказало, что тут кроется типичная и, главное, реальная задача линейного программирования, где целевая функция, которую нужно максимизировать, – суммарный объем краски, переменные – количество наполненных краской барабанов по 15 и 55 литров, которые нужно забрать, и три ограничения – (1) стоимость краски не должна превышать оговоренных с Тамбовэнерго 14 млн. рублей, (2) нельзя брать неполную банку (ограничение на целочисленность

переменных) и (3) количество банок разной вместимости не должно быть отрицательными числами[16]. Оля вызвалась помочь решить эту оптимизационную задачу и тут же с помощью калькулятора[17]

прикинула, что мне нужно взять 16 больших и 2 маленьких барабана, вмещающих 910 литров краски на сумму 13 млн. 814 тыс. рублей. Вспомнив, как я отчаянно торговался в Тамбовэнерго и все-таки увеличил цену программ с 12 до 14 млн. руб., я спросил у Оли, а можно ли не терять 186 тысяч – не оставлять их Тамбовэнерго. Она сказала, что нет, так как такие задачи решает чуть ли не каждый день, оптимизируя не только стоимость краски, но и ее загрузку в контейнеры различной вместимости[18], и что она «собаку съела» на решении таких проблем.



Наблюдая за «танцем» Олиных пальцев на кнопках калькулятора и за числами на его дисплее, я понял, что Оля использует так называемый «рабоче-крестьянский» и, главное, ненадежный алгоритм оптимизации: сначала выбирается краска в большой таре, а затем остаток денег (или объема контейнера) заполняется краской в маленькой таре. Примерно так мы пакуем чемодан, отправляясь в поездку, – сначала кладем в него крупные вещи, а потом напихиваем в пустые пространства всякую мелочь. Еще раз вспомнив Вийона (смотри сноску 17), я спросил у Оли, почему она не использует для решения таких задач компьютер и табличный процессор Excel, рабочий лист которого как будто специально был выведен на экран ее компьютера. Я тут же вызвался показать, как это делается. В среде Excel есть так называемый Решатель (Solver), диалоговое окно которого вызывается командой Найти решение... из меню Сервис.

В этом окне пользователь указывает ячейку, хранящую целевую функцию, значение которой нужно максимизировать, ячейки с переменными поиска (в начале оптимизации они либо пусты, либо хранят значения первого приближения к максимуму) и ограничения.

Алгоритм оптимизации с помощью Решателя Excel можно назвать «ленивым»: пользователь формирует таблицу расчета и говорит: «По щучьему велению, по моему хотению сделай так, чтобы»... целевая функция приняла максимальное (минимальное, определенное) значение, но при этом были выполнены все ограничения». Для этого пользователю достаточно нажать кнопку Выполнить. Решатель Excel выдал нам старый результат – 16 больших и 2 маленьких барабана. Но сдаваться не хотелось.

Есть хорошее правило – проверять решение задачи не только другими методами, но и другими программными средствами. Кроме того, не следует забывать о KISS-принципе программирования. С поцелуями он ничего общего не имеет, хотя хорошее отношение к решаемой задаче и к компьютеру в нем просматривается. KISS – это аббревиатура английской фразы: «Keep It Simple, Stupid! – Делай это проще, дурачок!» Она призывает решать поставленную задачу наипростейшими способами и прибегать к изощренным алгоритмам и методикам только тогда, когда простые способы не годятся из-за длительности времени счета или из-за нерационального использования других ресурсов человека и/или компьютера[19].



Простейший способ решить на компьютере поставленную задачу – это перебрать

все варианты и остановиться на оптимальном. Благо вариантов не так уж много – 1088: на отпущенные 14 миллионов можно было взять не более 63 маленьких барабанов с краской или не более 16 больших [20]. Перебор можно назвать «компьютерно-рабоче-крестьянским» методом решения. Но помимо прочего он может дать стопроцентную уверенность не только в правильности, но и в единственности

найденного решения и даже показать, что таких решений несколько. А такая ситуация нередка в задачах целочисленного

линейного программирования.

Итак, перебор. Следуя вышеописанному правилу, новый метод решения задачи необходимо совместить с новым программным средством для его реализации. Это, конечно, можно было сделать и в среде Excel, составив таблицу всех решений и/или написав программу перебора на языке Visual Basic for Applications (VBA), встроенном в Excel. Но у Оли на компьютере был установлен еще и Mathcad (феномен рояля в кустах). Он довольно успешно решает задачи самого разного плана (включая и экономические) без обращения к чистому программированию (BASIC, C, Pascal и др.). Кроме того, в то время я работал над книгой, которую читатель держит в руках. Пример с краской эту книгу только украсит (нечаянный каламбур).

Задача о краске

Протокол «контрольного взвешивания» краски в среде Mathcad приведен на рис. 3.11. Комментарии поясняют, что происходит в формулах. Во-первых, функция Maximize, как и ожидалось, дала дробный ответ (см. пункт 2) – маленьких банок можно не брать, если можно брать дробное количество больших. Пришлось, вспомнив эпиграф и название этюда, перейти к перебору вариантов. В Mathcad-документе формируются две матрицы с именами Об (пункт 3.2) и Ст (пункт 3.3), элементы которых (их 1088 – у матриц 17 столбцов и 64 строки) хранят значения объема (Об) и стоимости (Ст) краски в зависимости от комбинаций расфасовки. Далее (пункт 3.4) некоторым элементам матрицы Об присваиваются нулевые значения, если данные комбинации расфасовки не проходят по стоимости. Остальное – ловкость рук и никакой математики: в пункте 3.5 определяется номер строки (переменная N_15) и номер столбца (N_55) матрицы Об, на пересечении которых находится элемент с максимальным значением. Ответ (6 маленьких барабанов и 15 больших) неприятно удивил Олю. Она невольно обманывала меня на 5 литров краски и на 139 тыс. руб.

Метод поиска координат точки максимума, реализованный на рис. 3.11 (двойная сумма), имеет существенное ограничение: в анализируемой матрице (у нас это Об) должен быть только один максимальный элемент. Если их несколько, то ответ будет неверен: в переменные N_15 и N_55 будут записаны суммы координат точек с максимальным элементом. Мы это наблюдали в пункте 2 на рис 3.9.

Так Mathcad сэкономил мне почти полторы сотни тысяч рублей. Деньги не такие уж большие, но если присовокупить к ним новый компьютерный этюд в книгу, новую тему лекции и новую лабораторную работу по информатике, а также гонорар за эту книгу, то игра стоила свеч.

Вернувшись из Тамбова домой в Москву, я в спокойной обстановке у своего родного компьютера еще раз проанализировал задачу. И вот что получилось.

Во-первых, заставить Решатель Excel правильно «разъяснять» задачу о краске можно было, изменив начальные установки Решателя. А для этого нужно было не полениться и нажать на кнопку Параметры... в диалоговом окне Поиск решения. В новом диалоговом окне Параметры поиска решения достаточно было допустимое отклонение уменьшить с 5 до 1%. После этого правильное решение (15 больших и 6 маленьких барабанов) было бы найдено. Честно говоря, в Excel плох не Решатель, а его начальные установки. Очень мало пользователей Excel, прибегающих к услугам Решателя, нажимают кнопку Параметры... Тот же, кто разбирается в сути установок оптимизации, как правило, с Excel не работает. Отсюда и недоразумения.

Во-вторых, и Оля, и Excel, и Mathcad в разной степени меня немножко обманули[21]: 910 литров краски можно было отгрузить и другим вариантом – 13 маленьких и столько же больших барабанов[22]. В этом случае осталось бы «сдачи» всего 12 тыс. рублей. Более того, решение задачи о краске с новой целевой функцией (стоимость краски в банках) дает еще один результат: 37 маленьких и 6 больших барабанов, выбирающий еще одну тысячу из Тамбовэнерго.

Вариант расфасовки (число маленьких барабанов/число больших барабанов)	2/16	6/15	13/13	37/6
Объем краски (л)	910	915	910	885
Остаток невыбранных денег (руб.)	186 000	47 000	12 000	11 000

В-третьих, когда я показал эту таблицу в отделе снабжения МЭИ, то мне было сказано, что самый оптимальный вариант и для меня (мне важны деньги) и для МЭИ (ему нужна краска) четвертый: у Тамбовэнерго были бы выбраны почти все деньги, а 885 литров краски, как это ни кажется странным, больше, чем 910 и 915. Дело в том, что при крупной расфасовке много краски теряется из-за переливов в меньшую тару. 15-литровый барабан можно взять в ремонтируемую аудиторию и там полностью использовать.
Неверное решение задачи получается не только из-за плохих методик или дефектных программных средств, но и из-за того, что пользователь сам толком не знает, чего он хочет. Все программы решения задачи линейного программирования требуют четкого формулирования одной единственной целевой функции[23]. При решении учебных задач цель ясна. А что является целью в жизни? Но это уже не математика, а философия...
У метода перебора, реализованного на рис. 3.11, есть три собственных ограничения:
1) число переменных не может быть больше двух, так как в среде Mathcad есть векторы и матрицы, но нет тензоров (трех- и более мерных матриц);
2) при чрезмерном размере матрицы компьютер отказывается иметь с ней дело, выдавая протестующее сообщение типа «не хватает памяти»;
3) счет (если перебор можно назвать счетом) может длиться нестерпимо долго.
Первые два ограничения снимаются при переходе от метода формирования матрицы (рис. 3.11) к методу перебора вариантов с запоминанием только оптимального плана, который можно реализовать средствами программирования, что мы и сделаем в этюде 6 (см. рис. 6.31 и 6.32).
Метод перебора оказывается незаменимым (то есть опять же бывает не таким уж извращенным), когда задача, оставаясь целочисленной, теряет свою линейность[24]. В этом случае традиционные методы (например, симплекс-метод) часто оказываются бессильными.
Тем не менее реализация метода перебора в среде Mathcad всегда будет извращением чистой воды. Mathcad – это программа интерпретирующего типа с низкой скоростью выполнения исходного текста. Для перебора нужны не просто компиляторы, а компиляторы, оптимизирующие время выполнения программы.

Поиск места для ларька

На рис. 3.12 помещен протокол решения задачи о поиске места для ларька на дачном участке. Критерий поиска – минимум суммы расстояний от ларька до всех остальных домиков. Их координаты X и Y – случайные числа в интервале от 0 до 20 (наша задача учебная). Ларек может быть либо встроен в один из домиков (пункт 1), либо стоять отдельно (пункт 2). На рис. 3.12 координаты встроенного ларька определяются перебором. Затем эти координаты (Xiопт и Yiопт) становятся первым приближением для уточнения местоположения отдельно стоящего ларька. Заканчивается расчет графическим описанием и сути и решения задачи. Здесь главное – правильно отформатировать точки на графике. Поэтому выведено окно форматирования графика.

Вернемся к тестовым задачам на рис. 3.3-3.5.

На рис. 3.3 и 3.4 формируются матрицы М, элементы которых – значения анализируемых функций в узлах сетки, накрывающей точку минимума. Элементы матрицы М средствами Mathcad превращаются в линии уровня и в поверхность. Но эти матрицы могут сослужить нам и другую службу – координаты их минимальных элементов могут стать точками первого приближения к минимуму. Нащупать минимум (максимум) функции более чем двух аргументов (например, функции Пауэла – см. рис. 3.5) можно средствами программирования (см. этюд 6).

Транспортная задача, решенная нами на рис. 2.10, кочует из одного учебника в другой. Везде отмечается такой ее парадокс – по самому дешевому маршруту при минимизации затрат на перевозки ничего не возится. Если бы мы решали эту задачу вручную без компьютера, то сначала полностью загрузили бы дешевый маршрут, а потом все остальные. Этим парадоксом может воспользоваться хозяин транспортного предприятия, максимизировав свою прибыль от перевозок (см. рис. 3.13):

Транспортная задача (извращенное решение)

В этом случае второй по дороговизне маршрут (1200 у.е.) остается свободным – внешне все выглядит прилично.

Но парадокс задачи не в этом. Вернее, не только в этом. Дело в том, что она недостойна не только функций Minimize и Maximize, но даже и грубого перебора, так как сводится к решению простейшего уравнения:

с1м1+с2м1=40

Если с1м1=0, то с2м1=40, и затраты на перевозки максимальны. Если с2м1=0, то с1м1=40, и затраты максимальны. Рис. 2.10 и 3.13 – это чистой воды извращения. Или неумение либо нежелание подумать как следует над задачей.

Логические операторы и функции

Во-первых, булевы функции в среде Mathcad можно определить. Математика (см., например, «Справочник по математике для научных работников и инженеров» Корн Г. и Корн Т.) оперирует одной

одноместной (с одним аргументом) и семью

двухместными (с двумя аргументами) булевыми функциями. Все они определены в пунктах 0-7 на рис. 3.14. Если булеву переменную уподобить выключателю с двумя позициями («вкл» и «выкл»), то конъюнкция

– это последовательное соединение выключателей (пункт), а дизъюнкция – параллельное. Электрический аналог эквиваленции (пункт 3) может очень пригодиться для освещения длинного коридора, свет в котором зажигается и тушится независимо в двух его концах двумя выключателями.

В пункте 8 на рис. 3.14 сформирована трехместная булева функция с именем Решение, возвращающая вердикт жюри из трех человек: решение проходит, когда «за» голосуют двое или трое. Воздерживаться или уклоняться от голосования нельзя.

Функция Решение (программная реализация процедуры голосования) в пункте 8 на рис. 3.14 также имеет электрический аналог (аппаратная реализация – машинка для голосования) – комбинацию выключателей, соединенных последовательно и параллельно.

Двухместные булевы функции (пункты 1-7 на рис 3.14) имеют четыре (22) комбинации значений аргументов (таблица истинности), трехместные – уже 8 (23), одноместная, естественно, только две (21) – 0 или 1. Самих же двухместных булевых функций может быть 16 (42 – мы описали только семь), трехместных уже 64 (43 – мы описали только одну). Одноместных булевых функций четыре (41 – мы описали только одну). Вот другие три одноместные булевы «функции» y2(x):=1, y3(x):=0 и y4(x):=x. Но никакой практической ценности в программировании они не имеют: первые две (y2 и y3) – это константы, а y4 – это просто сам аргумент. Ненаписанные нами остальные девять (16-7) двухместные булевы функции (там тоже есть константы) имен не имеют и, как правило, ни в математике, ни в программировании не применяются.

В математике булева функция выдает два значения (0 – 1, да – нет, истина – ложь и т.д.), в программировании же – минимум три: да, нет и... аварийный останов, связанный с ошибкой (один или несколько аргументов не определены). Такую ошибку можно обработать (в Mathcad для этого служит оператор on error) и пустить расчет по третьему пути. Одноместных булевых функций может быть больше четырех. Как понравится такая функция: y5(x):=if(rnd(1)>0.7, 1, 0), возвращающая единицу с вероятностью 30%, и нуль – с вероятностью 30%.

Функцию Решение можно построить намного проще – вычислить среднее арифметическое значений аргументов. Эту работу выполняет встроенная Mathcad-функция mean. Если оно окажется больше, чем 0.5 – то решение принято (возвращается единица), нет – нуль:

Решение(V):= mean(V) > 0.5

Число аргументов новой функции Решение, таким образом, допустимо увеличивать, не прибегая к сложному дереву булевых операций, показанных в пункте 8 на рис. 3.14.

В пункте 9 на рис. 3.14 формируется еще одна функция Решение для голосования комитета с любым числом членов, принимающих решение большинством голосов. Но при этом часть голосующих обладает правом вето

(пример – Совет Безопасности ООН где, как писал Джорж Оруэл: «все равны, но некоторые равнее»). Люди (или страны: США, Россия, Китай, Франция и Великобритания, если иметь в виду СБ ООН) с правом вето у нас объединены в вектор Const (постоянные члены СБ), а все остальные – в вектор Var. Если для принятия решения большинством голосов годится среднее арифметическое, то для блокировки принятия решения – среднее геометрическое (gmean): корень n-й степени из произведения n сомножителей. Эта встроенная функция появилась только в восьмой версии Mathcad. При этом gmean требует, чтобы все элементы вектора (матрицы) аргумента были ненулевыми. Поэтому в пункте 9 на рис. 3.14 мы сначала переопределили функцию gmean так, чтобы она «проглатывала» и нулевые элементы вектора-аргумента, а потом уже с ее помощью сформулировали функцию Решение для электората типа СБ ООН. В конце пункта 9 показаны три типичных исхода голосования:

— решение принимается большинством голосов;

—    решение проваливается одним человеком с правом вето;

—    решение не проходит, так как большинство против.

Конечно, использование среднего геометрического для подсчета голосов – это чистой воды извращение (см. название данного этюда). Тут можно использовать функцию And – просто логическое умножение безо всякого корня. В пункте 10 на рис. 3.14 сформулированы функции And и Or, аргументы которых – векторы-столбцы с переменным числом элементов[26].



Этой главке автор хотел дать и другое название – «Казнить нельзя помиловать». Но уж больно оно избитое. Традиционно читателя просят поставить запятую в этом предложении[27]

и проследить, как меняется смысл вердикта в зависимости от места такого невинного знака препинания.

А как вам понравится такой ответ на вопрос о месте запятой: запятую нужно «размазать» по предложению – n процентов запятой поставить после слова «казнить», а 100-n – после слова «нельзя». Трактовать такую новую грамматическую (пунктуалистическую?) конструкцию можно по-разному. Но сначала поговорим о самой постановке вопроса.

Один лидер «третьего рейха» любил повторять, что он всегда хватается за пистолет, слыша слово «культура». Сталкиваясь с логической задачей, программисты «хватаются» за троицу булевых функции Not, And, Or и т.д. Но их-то и нет в списке встроенных

функций Mathcad. Нет там и булевых (логических) переменных. Тут программист чертыхнется (а зря – см. ниже) и напишет соответствующие пользовательские функции (см. пункты 0 – 7 на рис. 3.14), заставляя числовые[28]

переменные выполнять по совместительству и роль булевых. После этого ничего не стоит написать булеву функцию Решение, возвращающую единицу

(логическое «Да») или нуль («Нет») в зависимости от итогов голосования – решение принимается, если двое или трое присяжных проголосуют «За».

Возвращаясь к дилемме «казнить-помиловать» и допуская совмещение должностей присяжного, судьи и палача, можно попытаться заменить в схеме пункта 8 электрическую лампочку на... электрический стул. Говорят, что подобная схема рубильников на самом деле запитывает американское орудие казни. Каждый из трех, приводящих приговор в исполнение, надеется, что он включил не настоящий рубильник, а муляж рубильника.

Еще немного об «электрических цепях». Последнее время в быту получают распространение выключатели, плавно меняющие накал лампочек от нуля до ста процентов. Еще раньше такие устройства (реостаты) стали применяться в театрах и кинозалах. Медики уверяют, что плавный переход от света к темноте через полумрак благотворно влияет на зрение.



А можно ли подобными регуляторами заменить выключатели в вышеприведенной схеме аппаратной реализации процедуры голосования? Может ли функция Решение иметь не только логические, но и вещественные аргументы и возвращать вещественное значение, плавно меняющееся от нуля до единицы (от 0 до 100%)? Очень часто, осуждая или оправдывая кого-либо, трудно прийти к однозначному решению. Даже на первый взгляд явное преступление может иметь такую оценку – «это скорее беда, чем вина подсудимого». Но людей, принимающих решения, по-прежнему заставляют давать только черно-белые оценки[29].

Толерантность[30]

сначала проникла в религию. Человечество, нахлебавшись крови в религиозных войнах[31], относительно поумнело. Сейчас цивилизованный человек может сказать о себе, что он на k процентов атеист, на l процентов мусульманин, на m процентов – католик, а на n процентов – протестант (гугенот – вспомним Варфоломеевскую ночь и Париж, который стоил мессы). И не обязательно, чтобы k+l+n+m равнялось ста процентам. Во многих церквях Америки по пятницам служит мулла, по субботам – раввин, а по воскресеньям – священник (поп, пастор, ксендз) и никого это не шокирует. Затем толерантность охватила мир искусства, размыв систему классических канонов и стилей. Сейчас главное – это талант художника и то, что он хочет сказать миру. И не важно, кто он – реалист, импрессионист (нео-, пост- и т.д.) или просто примитивист, впервые взявшийся за кисть в 70 лет. Теперь стали говорить и о терпимости в науке. Ее проявления – теория нечетких множеств

(fuzzy sets – см. рис. 6.41-6.45 в этюде 6) и теория нечеткой логики (fuzzy logic). Неоднозначность оценок стала превалировать не только в гуманитарных дисциплинах (см. сноску 27 с деликатной подсказкой Word’а), но и в точных науках – в математике, например. Автор где намеренно, а где по незнанию (по недопониманию – хороший пример нечеткого множества в живом языке) не совсем верно трактует положения теории нечетких множеств. Раньше бы такого автора с кашей съели. А теперь ничего – публикуют, читают.



Но это, конечно, не значит, что размываются все грани черно-белых оценок. Об этом хорошо сказано у Пушкина:

Ах! Чувствую: ничто не может нас

Среди мирских печалей успокоить;

Ничто, ничто… едина разве совесть.

Так здравая она восторжествует

Над злобою, над темной клеветою. –

Но если в ней единое пятно,

Единое, случайно завелося,

Тогда – беда! Как язвой моровой

Душа сгорит, нальется сердце ядом,

Как молотком стучит в ушах упрек,

И все тошнит, и голова кружится,

И мальчики кровавые в глазах…

С другой стороны у Ф.М.Достоевского в «Скверном анекдоте» читаем: «Был он и честен, то есть ему не пришлось сделать чего-нибудь особенно бесчестного…».

Давайте посмотрим, как нашу задачу о голосовании можно решить с учетом положений теории нечеткой логики (пункт 10 на рис. 3.14). Задачу можно обогатить элементами нелинейности, приняв во внимание условное деление голосующих на консерваторов (k), традиционно склонных к осуждающим приговорам, центристов (c) и либералов

(l – эль). Степень радикальности жюри присяжных (парламента и вообще любого электората) будем учитывать через коэффициент k. Голосующие устанавливают степень своего решения «за» (от 0 до 1), но на исход голосования влияют функции yk, yc и yl, демпфирующие крайние оценки (см. пункт 10.1).

«Цветная» функция Решение, построенная на функциях min и max (см. пункт 10.2), при логических значениях аргументов (0 или 1) полностью эквивалентна своему «черно-белому» аналогу, использующему функции And и Or (см. пункт 8). Встроенные функции min и max способны работать и с логическими, и с вещественными, и даже с комплексными[32]

аргументами. Кроме того, функции min и max удобны еще и тем, что их аргументами может быть вектор-столбец (аргумент функции max в пункте 10.2), вектор-строка (min) и даже матрица (см. рис. 6.34 в этюде 6). Это позволяет комбинировать типы аргументов (горизонталь-вертикаль) создаваемой «цветной» логической функции, делая ее более компактной и более легкой для понимания. (Здесь вызывается не функция, а постфиксный оператор – это позволяет убрать лишние скобки.)



Ладно, скажет читатель, а что делать с вердиктом присяжных такого рода: «Виновен на 57%, невиновен на 43%»? Что делать? Смотреть на графики, материализующие «цветное» решение!

В пункте 10.2 на рис. 3.14 визуализированы вердикты присяжных при фиксированном решении либерала 0.5 (воздержался – ни то ни се).

Интерпретация цвета участков поверхности решения (здесь, к сожалению, не цвета, а оттенки серого) может быть такая:

красный цвет графика говорит сам за себя – кровь, «вышка»;

оранжевый – пожизненное заключение;

желтый – каторга;

зеленый – тюремное заключение;

голубой – условное осуждение;

синий – общественное порицание;

фиолетовый – невинен.

Цветовую палитру («Каждый охотник желает знать, где сидят фазаны!») можно сдвигать, учитывая тенденции в общественном сознании и изменения в законодательстве – мораторий на смертную казнь, например. При этом нужно будет «сдвигать вниз» (в холодные тона) и другие виды наказаний. В наших тюрьмах условия содержания такие, что смертная казнь может оказаться просто наградой. Основной довод противников смертной казни в том, что жизнь – это Дар Божий, и только всевышний может приговорить к высшей мере. Но и свобода не меньший дар! Второй довод в том, что смертная казнь делает невозможным исправление судебных ошибок. Но. Отсидел человек 20 лет в камере пожизненного заключения, а ему говорят, пардон, мы ошиблись. Кто вернет загубленную жизнь.

Строить «цветные» логические схемы поможет и нечеткая функция Not:

Not(x):=½1-x½ или ½100-x½.

В пункте 10.3 на рис. 3.14 функции max и min заменены на их «аналоги» – на функции mean (среднее арифметическое) и gmean (среднее геометрическое). Поверхность стала более гладкой – природа, как мы знаем, не терпит острых углов.

В пункте 11 на рис. 3.14 сформированы многомерные функции And и Oг. Но записать допустимо еще проще:

And(x):=min(x)          Or(x):=max(x),

А можно работать только с min и max, которые хорошо справляются и с булевыми (четкая логика), и с вещественными (нечеткая логика) аргументами. Но если пользователь оптимизирует программу (см. главку 6.12), то вместо функции min лучше использовать оператор умножения. Дело в том, что при умножении сразу возвращается нуль, если первый сомножитель нулевой. Функция же min излишне педантична – она перебирает все элементы своего аргумента-матрицы (вектора).

Но увлекаться статистическими функциями (min, max, mean, gmean, rnd, var и др.) при реализации логических схем нужно осторожно. Уинстон Черчиль говорил, что есть Большая Ложь, Просто Ложь и… Статистика – героиня этого этюда.

Функция «Победитель»

Что происходит в функции Победитель?

В начале дуэли все участники живы: все три элемента вектора Статус принимают значение “жив”[50]. Далее проводится жеребьевка: определяется направление очередности выстрелов (если переменная Очередь равна единице, то очередность идет в таком направлении ...0®1®2®0®1®2.., если минус единице – ...0®2®1®0®2®1) и определяется первый стреляющий (переменная Стрелок). Кроме того, обнуляется переменная Убийство, по которой прерывается цикл выстрелов в дуэли.

Математическая модель дуэли опирается на цикл с выходом из середины (while ... break…): дуэль продолжается, пока не будут сделаны два результативных выстрела. В теле цикла while определяется Цель – самый меткий противник, которого убивают (СтатусЦель

¬ “убит”), если, во-первых, не промахиваются (МеткостьСтрелок

> rnd(1)) и (And), во-вторых, не (Not) стреляют намеренно в воздух. Второе имеет место при хитрой тактике стреляющего (ТактикаСтрелок = 2) и (And), если метких противников более одного.

Определение следующего стреляющего ведется в цикле с постпроверкой (while ... break): цикл прерывается, когда, перебирая очередь, отмеченную выше (...0®1®2®0®1®2.. или ...0®2®1®0®2®1...), «натыкаются» на живого участника.

Возвращает функция Победитель номер участника дуэли (0, 1 или 2), оставшегося в одиночестве (значение переменной Стрелок по выходу из цикла).

Функция Победитель возвращает непредсказуемое целочисленное значение 0, 1 или 2, так как в ней в трех местах вызывается встроенная в Mathcad функция rnd, которая возвращает псевдослучайное число в интервале от нуля до значения аргумента функции rnd. Этот аргумент у нас равен либо единице (случайный выбор очередности выстрелов и имитация выстрела с вероятностью попадания, пропорциональной меткости стреляющего), либо трем (случайный выбор первого стреляющего – здесь дополнительно работает встроенная функция floor, возвращающая у положительного вещественного числа его «пол» (в смысле не «потолок» – по-английски a floor): floor(0.54), floor(1.82), floor(2.48) = 0...

Ввод и сортировка двух векторов

В пункте 1 на рис. 4.1 переменным X и Y присваиваются транспонированные векторы-строки, а не просто векторы-столбцы. Это делается для компактности записи. Кроме того, элементы векторов имеют лишние нули – 4.0 вместо 4 и т.д. За счет этого выравниваются по вертикали пары значений Xi и Yi. Без такой маленькой хитрости рано или поздно пары собьются, что будет мешать их просмотру и редактированию. Альтернативное решение этой проблемы – хранение пар данных в матрице с двумя строками и с числом столбцов, равным числу пар[1].

Считается, что программиста от простого смертного можно отличить по простому тесту. Если программиста поставить в голову шеренги и приказать: «По порядку рассчитайсь!», то программист сначала уточнит, по какой системе нужно рассчитываться (двоичная, восьмеричная, шестнадцатеричная, десятеричная[2]...), а потом выкрикнет: «Нулевой!» В среде Mathcad по умолчанию номер первого элемента вектора (первого ряда и первого столбца матрицы) нулевой. Именно поэтому при семи экспериментальных точках, координаты которых заносятся в векторы X и Y, константа N равна шести (феномен программиста в строю). Номер первого элемента массивов и векторов хранится в системной переменной ORIGIN (an origin – начало, источник), значение которой (по умолчанию оно нулевое) в Mathcad-документе можно изменять (ORIGIN:=1, например). Допустимо менять и второе умолчание «шеренги» – систему счислений.

Ввести в среде Mathcad переменную-вектор можно двумя различными способами (см. этюд 1): отдачей команды Matrices из меню Math (Insert – Mathcad 7 и 8) либо нажатием на панели математических инструментов кнопки с изображением матрицы (щелкнув по ней курсором мыши) – см. рис. 1.7. Ввод за переменной ее индекса также допустим двумя способами: нажатием на панели математических инструментов на кнопку-иероглиф «Переменная с индексом» или набором за именем переменной символа открывающихся квадратных скобок (рудимент языков Pascal и C, где квадратные скобки означают индексную переменную).

Векторы X и Y совсем не обязательно вводить в Mathcad-документ вручную с клавиатуры. Если экспериментальный стенд оборудован средствами АСНИ (автоматизированной системой научных исследований) и данные с приборов заносятся на магнитный диск, то Mathcad-выражение X:=READPRN(имя файла) поможет считать их и оформить в виде Mathcad-вектора (матрицы) с именем X[3]. Кроме того, не следует забывать, что Mathcad – это полноценное Windows-приложение со встроенными средствами обмена в статике и динамике (Clipboard, DDE, OLE). Объемную задачу можно решить лишь тогда, когда голос Mathcad звучит в стройном хоре других приложений (графические, текстовые и табличные процессоры, базы данных, языки программирования и т.д.).

Линейное сглаживание

Задача аппроксимации, и не только линейной – это типичная оптимизационная задача (см. этюды 2 и 3 и линии уровня в пункте 3.2 на рис. 4.2), сводящаяся к поиску минимума целевой функции СКО (среднеквадратичное отклонение) двух переменных a и b. В свою очередь, линейное сглаживание сводится к решению системы линейных алгебраических уравнений (см. этюд 1 и пункт 3.3 на рис. 4.2), состоящей из приравненных к нулю частных производных функции СКО по коэффициентам a и b.

Решение, показанное в пункте 3.2, предпочтительней для сферы образования – оно как бы «кричит» о сути метода наименьших квадратов: в функции СКО фигурирует квадрат, а сама функция минимизируется.

Определение точки с максимальным отклонением от прямой

Найденные тем или иным способом значения коэффициентов a и b сглаживающей функции y(x) = a + b×  x позволяют построить на графике прямую с роящимися вокруг нее точками (у нас квадратиками – рис. 4.3). Подобным графиком на практике, как правило, завершают обработку экспериментальных данных: график, во-первых, даст наглядное представление о качестве сглаживания, а во-вторых, поможет в случае чего отловить допущенные ошибки ввода исходных данных (пропуск десятичной точки, например). Этой цели может служить и предварительная сортировка векторов (см. пункт 2 на рис. 4.1): ошибочные значения (промах эксперимента, неправильный ввод данных) часто всплывают на концах упорядоченного вектора. В-третьих, график сам по себе ценен. С помощью графика, то есть с другого конца, можно довольно быстро решить задачу линейного сглаживания. У автора в лаборатории есть сотрудница, у которой глаз-алмаз: она при помощи тонкой прозрачной линейки так проводит прямую вблизи экспериментальных точек, что по ней можно определить коэффициенты a и b с точностью не меньше трех процентов (толщина карандашной линии).

Несколько слов о графических возможностях Mathcad и других подобных пакетов. Если студент начнет строить график функции по технологии, заложенной в математическом пакете, то автор выгонит такого студента с занятий, да притом вослед будет улюлюкать и топать ногами. Все (скажем осторожнее – почти все) математические пакеты при построении графиков никак (почти никак) не используют элементы искусственного интеллекта, а просто сканируют значение аргумента и проставляют точки с заданным пользователем шагом или с шагом, определяемым разрешением дисплея (принтера). Студентов же учат совсем другому – анализу функции, поиску характерных точек (корней, минимумов, максимумов, точек перегиба и т.д.), опираясь на которые и строится график: парабола, гипербола или какая-нибудь там лемниската Бернулли (см. рис. 1.18 в этюде 1). Но Богу – Богово, кесарю – кесарево, машине – машиново. Беда многих преподавателей в том, что они относятся к математическим пакетам не как к инструментальным средствам, требующим определенной сноровки и навыка (и головы, конечно), а как к своим своеобразным коллегам, которых на пушечный выстрел нельзя подпускать к студентам, изучающим математику, дабы они (студенты) не набрались от них (от пакетов) разных глупостей. Дежурная фраза одной знакомой автора: «Mathcad – круглый дурак, Maple – полный кретин, Mathematica – законченная идиотка».

Нелишне дополнить результаты сглаживания указанием точки, максимально отклонившейся от прямой (см. рис. 4.3). Само значение такого выброса найти несложно через функцию max. А вот с определением координат этой точки придется повозиться: привлечь аппарат булевых выражений, принимающих два значения – True (в среде Mathcad – единица) и False (нуль), умножение которых на текущий индекс фиксирует искомую координату.

В пакете Mathcad более 50 встроенных операторов (см. приложение 2) и почти 300 функций (см. приложение 3). Пять встроенных функций (csort, intercept, slope, min и max) были задействованы в задачах на рис. 4.1-4.3. Когда программисту предстоит решать какую-либо локальную задачу, то перед ним часто встает альтернатива: кодировать ли решение прямо в программе или выносить его наружу, оформляя в виде процедуры (функции). Считается, что глупый человек учится на своих ошибках, а умный – на чужих. Начинающий программист пишет свои процедуры (функции), а опытный ищет их в наборе ранее созданных. Знание пакета Mathcad – это на 90% знание операторов и функций[6], в него встроенных. Остальное – ловкость рук и программирование (средство создания новых инструментов – см. этюд 6).

Есть три причины, заставляющие даже сверхумного программиста отказываться от готовых программных форм и «изобретать велосипед». Первая причина лежит в сфере образования: тексты программ должны быть прозрачными для обучаемых. Во-вторых, в открытый участок программы легко ввести дополнения и изменения, расширяющие сферу ее применения и/или снимающие ранее наложенные ограничения. Так устроен, к примеру, пакет MatLab (разработка фирмы The Math Works). В его состав входят исходные тексты на языке C всех встроенных процедур и функций, так что пользователь перед включением их в работу может что-то узнать о методах, заложенных в них, и/или прощупать их работоспособность. В-третьих, всегда есть опасения, что в готовую программную форму затесалась чужая ошибка, которая, как бомба замедленного действия, может взорвать всю программу в самый неподходящий момент – после сдачи готового программного продукта заказчику или после того, как он разойдется по дилерской сети. Пример у нас под рукой (рис. 4.3). При всем богатстве встроенных функций пакету Mathcad не хватает функции определения в векторе или в матрице координат минимального (максимального) элемента. Выход из положения – это сумма (для вектора) или двойная сумма (для матрицы) произведений номера текущего элемента на булево выражение (см. рис. 4.3). Эту конструкцию так и хочется оформить в виде новой функции с именем imax, например, и больше с такой задачей не возиться. Но в новую функцию перекочует и будет замаскирована ошибка – неясно, что будет возвращать новорожденная функция imax, если в аргументе-векторе (в массиве) два или более максимальных элементов. Из прозрачной формулы с суммой это понятно, а из «затененной» функции imax – нет. Все эти замечания можно отнести и к встроенным функциям intercept и slope, возвращающим значения коэффициентов сглаживающей прямой. Всегда остаются сомнения, а нет ли в этих функциях фактической или методологической ошибки. Последнюю можно обнаружить, если подставить в функции intercept и slope аргументы-векторы с двумя или даже одним элементом. Через две точки всегда можно провести прямую. Через одну точку прямых можно провести бесчисленное множество. И в том, и в другом случае сумма квадратов отклонений двух точек (одной точки) от прямой будет минимальной (нулевой), и требования метода наименьших квадратов будут выполняться абсолютно. Но в первом случае функции intercept и slope будут решать простую интерполяционную задачу, для которой в среде Mathcad есть особый математический аппарат (см. ниже). Во втором случае (X и Y – не векторы, а скаляры) функции intercept и slope должны выдавать бесчисленное множество значений, связанных ограничением Y = a + b × X. В плане выполнимости критерия наименьших квадратов здесь все безупречно, но методология, заложенная в функции intercept и slope, приводит к тому, что при числе элементов в векторах X и Y, меньшем двух, выдается сообщение об ошибке. Но все это слабая защита, которую пользователь легко может обойти, подсунув функциям intercept и slope более одной точки, но с повторяющимися значениями аргументов. Резюме: играть можно не только с игровыми программами. На эту роль подходят и серьезные математические пакеты – было бы желание у пользователя. Компьютер же, как здоровая молодая собака, всегда готов играть со своим хозяином. Замахнется, к примеру, человек палкой, но не бросит ее, – собака прыгает, вертит головой, но не знает, куда бежать. Подсунет пользователь машине хитрый аргумент – функция не знает, что с ней делать, и выдает какие-то странные сообщения об ошибках, веселящие пользователя.

Есть направление в искусстве под названием поп-арт – популярное искусство. Методика обработки статистических данных, показанная на рис. 4.2, может быть названа поп-статом.

Аппроксимация полиномом 3-й степени

На рис. 4.4 формируются матрица A коэффициентов при неизвестных и вектор B свободных членов системы четырех линейных алгебраических уравнений, к которой сводится задача об аппроксимирующем полиноме третьей степени (кубическом). Сама система может решаться либо матричными операторами (a:=A-1×B), либо обращением к встроенной функции lsolve (см. пункт 3.3.2 рис. 4.2). Полноценный программный пакет всегда должен предоставлять пользователю возможность сделать какую-либо операцию двумя, а еще лучше тремя различными способами. Пользователь будет чувствовать себя комфортно в программной среде, если его право выбора не ограничено. На выбор же могут влиять не только сомнения в качестве тех или иных готовых инструментальных средств (см. выше) или нечеткое знание области их применения, но и вкусовые предпочтения пользователя. Решение системы линейных алгебраических уравнений (базовая задача любого Решателя) через матричные операторы неудобно тем, что пользователь все время напарывается на сообщения об ошибках, набирая R:= B / A или R := B × A-1. Крамольность первого выражения очевидна – в математике нет понятия матричного деления. Но почему нельзя писать R := B × A-1, знают далеко не все. Так или иначе, о KISS-принципе не следует забывать. Помнить следует и другое предостережение, зафиксированное в пословице: «Простота хуже воровства». Выкладки рис. 4.4, от которых рябит в глазах из-за обилия «сигм», можно упростить вводом переменных с индексом Ak,m и Bk (рис. 4.9). Но! Автор уже раз обжегся на суммировании в среде Mathcad, когда рассматривал систему искусственного интеллекта SmartMath (рис. 7.15 в этюде 7): за суммой, особенно тройной с пересекающимися индексами, может таиться ошибка.

Сглаживание с использованием функции linfit

Аргументы функции linfit – числовые векторы X и Y и вектор-функция f, хранящая набор пользовательских сомножителей (на рис. 4.5 – это 1, 1/x, 1/x2 и 1/x3), коэффициенты которых функция linfit возвращает в вектор a, опираясь на метод наименьших квадратов (см. рис. 4.5).

Нелинейное сглаживание

1. В среде Mathcad есть функция genfit (GENeral FITting – общее сглаживание), допускающая множество параметрических коэффициентов у сомножителей произвольного вида. Она, в отличие от функции linfit, решает нелинейную[7]

задачу аппроксимации. Пример использования функции genfit дан в пункте 7.1 на рис. 4.6. В функцию-вектор f необходимо занести не только само сглаживающее выражение (у нас это экспоненциальная функция), но и его частные производные[8] по искомым параметрам a0 и a1,.объединенным в вектор. Из-за того, что нелинейная задача может иметь более одного решения, функция genfit требует начального приближения (третий аргумент-вектор), вблизи которого и ищется одно из решений.

2. Без функции genfit задачу нелинейной аппроксимации, как правило, решают линеаризацией

исходных данных, подключая к работе уже известные нам функции intercept и slope. В нашем случае (пункт 7.2 на рис. 4.6) при исходном уравнении Y=a × x b  встроенные функции intercept и slope прикладывают к новому уравнению Ln(Y)=Ln(a)+b×Ln(X). Но это приводит к некоторому искажению математической модели: сумма X и сумма логарифмов X – это далеко не одно и то же.

3. В ряде случаев при решении задачи нелинейной аппроксимации можно обойтись и без функции genfit (пункт 7.1 рис. 4.6), и без искажающей линеаризации (пункт 7.2), применив открытый алгоритм поиска значений коэффициентов a0 и a1, минимизирующих целевую функцию – сумму квадратов отклонений точек от кривой. Расчет, показанный в пункте 7.3 на рис. 4.6, кроме того, не требует знания частных производных сглаживающего уравнения.

В конце рис. 4.6 приведено графическое сравнение трех методов нелинейного сглаживания. Из графика видно, что линеаризация исходных данных (пункт 7.2) привела к существенным искажениям результата. Поиски же параметрических коэффициентов через функцию genfit (пункт 7.1) и через минимизацию (пункт 7.3) близки по результатам.

Практический совет по выбору наиболее подходящей формулы для сглаживания. В Mathcad-документе можно хранить набор формул, подключая одну из них по мере надобности к статистической обработке экспериментальных точек. В диалоговом окне Properties (свойства – оно вызывается командой Properties в меню Format) есть переключатель Disable Evaluation (Запретить вычисления), позволяющий превращать математические выражения[9]

в комментарий:

Данный переключатель превращает выражение в комментарий (что отмечено черным квадратиком правее выражения) и переопределяет тем самым функцию пользователя. О втором переключателе (Enable Optimization – Разрешить оптимизацию) будет рассказано в этюде 7 (раздел 7.3).

В Mathcad-документе можно записать множество функций пользователя, подключая одну из них к аппроксимации: линейной (рис. 4.2), экспоненциальной (рис. 4.6), логарифмической и т.д., и подбирая тем самым наилучшую модель обработки экспериментальных данных. Выбор формулы можно вести и без переключателя Disable Evaluation, опираясь на свойство среды Mathcad включать в расчеты только последнюю запись функции. Нужную функцию можно просто перетаскивать (технология drag-and-drop) в конец списка.

Интерполяция сплайном

Отличия в линейной (lspline), параболической (pspline) и кубической (cspline) интерполяции сплайном заметно проявляются только на концах отрезка X1-XN. Эти области на рис. 4.8 рассмотрены «под лупой». Здесь нужно говорить уже не об интерполяции, а об экстраполяции (см. ниже рис. 4.14)

Несложно через точки провести полином N-й степени (рис. 4.9):

Интерполяция полиномом

Но нанизать опытные точки на интерполяционный «шампур», напрочь игнорируя неизбежные ошибки эксперимента, может только совсем безграмотный исследователь. У интерполяции другие сферы применения. Расскажем об одной из них. При решении в среде Mathcad какой-либо задачи нередко образуется составная функция[10], обращение к которой вызывает длинную цепочку сложных вычислений, связанных с поиском корней уравнения, с дифференцированием, интегрированием и т.д. Работать с такой функцией становится невмоготу даже на мощном компьютере. Один из выходов – омолаживание «бабушки»: табулирование «тормозной» функции с последующей заменой ее на эрзац-функцию, опирающуюся на интерполяцию – линейную, нелинейную или сплайном. И что удивительно, «омоложенная» функция, хоть и теряет напрочь свою физику, но в особых условиях может возвращать более точное значение, чем ее прародительница, в которой накапливаются ошибки численных методов. Узлы же интерполяции можно просчитать на пределе точности.

Двухмерная сплайн-интерполяция[11]

Далее автор приводит несколько пронумерованных «Советов тем, кто работает с Mathcad», которые публикуются в журнале КомпьютерПресс – на бумаге и на прилагаемом к журналу лазерном диске.

Педагогический опыт автора[12]

говорит о том, что студенты, выполняющие термодинамические расчеты, очень часто ошибаются в размерностях: складывают, например, джоули с британской единицей теплоты, а ответ записывают в калориях, забывая о соответствующем пересчете. Мы этой темы уже подробно коснулись в этюде 1. Среда Mathcad позволяет правильно (с соответствующими пересчетами) оперировать размерными величинами и «ругается» только в крайних случаях, когда, например, складывается длина с массой. Наша пользовательская функция hss(T, P) возвращает размерную величину (удельная энтальпия перегретого водяного пара), а ее аргументы (давление и температура пара) – также размерные величины.

Примеры работы двухмерной сплайн-интерполяции

На рис. 4.13 приведен пример формирования с помощью одномерной сплайн-интерполяции еще одной важной термодинамической функции одного аргумента – зависимости удельного объема кипящей воды от ее температуры.

Пример одномерной сплайн-интерполяции

Сплайн-интерполяция особенно критична на границах отрезка (области) существования аргументов. Вне этих границ речь идет уже не об интерполяции, а об экстраполяции – о предсказании значений функции за границами отрезка.

На рис. 4.14 показана работа функции predict, с помощью которой предсказывается

поведение какой-либо зависимости.

Экстраполяция

У функции predict (prediction – предсказание) три аргумента: вектор имеющихся данных (у нас 100 значений функции y(x) на интервале от 0 до 99 с шагом 1), число последних данных, учитываемых в предсказании (у нас их 50) и число предсказываемых данных (100). На графике на рис. 4.14 толстая кривая – функция y(x) на интервале 0-99, тонкая кривая – функция y(x) на интервале 100-199, а квадратики – предсказанные значения (не все, а только кратные 5), которые где-то в районе 160-170 обрываются.

Задание читателю, подготавливающее его к чтению следующего этюда, где будет описана математическая модель одной финансовой операции, – предсказать курс доллара на будущую неделю, опираясь на данные предыдущего месяца или года.

На рис. 4.15 проиллюстрирована работа сглаживающей функции supsmooth. Решается такая задача – сгладить функцию стоимости, например, комплектующих компьютера (см. задачу на рис. 6.33-6-35) в зависимости от объема закупки (скидка оптовикам).

Оценка качеств менеджера (начало)

В пункте 1 на рис. 4.16 оценки экспертов введены в матрицу M, содержащую девять строк (число экспертов n, j=1..9) и десять столбцов (число качеств m, i=1..10).

Пятибалльная средневзвешенная оценка деловых качеств менеджера определяется по формуле:

                                                      (4.1)

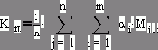
где m – количество оцениваемых качеств, i := 1, 2.. m,

n – число экспертов, j := 1, 2.. n,

Мj,i – оценка j-м экспертом i-го качества в баллах,

ai – весовой коэффициент для i-го качества.

Весовые коэффициенты определяют относительную значимость качеств: если i-е качество представляется незначимым, то весовой коэффициент ai равен нулю. Придание коэффициенту

ai значения, равного единице, делает незначимыми все остальные качества. Весовые коэффициенты должны удовлетворять следующему условию:

                                                                             (4.2)

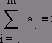
Значения весовых коэффициентов могут быть установлены различными способами:

лицом, принимающим решения (ЛПР);

экспертом с соблюдением условия (4.2);

по результатам экспертных оценок качества, косвенно отражающих мнения экспертов о значимости оцениваемых характеристик.

В последнем случае весовые коэффициенты рассчитываются по формуле:

                                              (4.3)

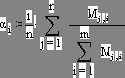
Вычисленные значения весовых коэффициентов в табличной и графической формах представлены в пункте 3 на рис. 4.17.

Оценка качеств менеджера (окончание)

Средневзвешенная оценка качества менеджера в баллах (пункт 4 на рис. 4.17) ¾ Kм = 4.162.

Алгоритм определения весовых коэффициентов ai влияет на оценку качества, которая может быть выполнена по выбору ЛПР на основе гипотезы равной значимости весовых коэффициентов:

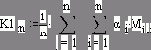
где ai = 1 / n.

В этом случае оценка качества значительно возрастает (в сравнении со средневзвешенной оценкой) – K1м

= 4.593.

Значения весовых коэффициентов могут быть установлены с учетом специфики конкретного заказа из условия приоритета  качеств (требуется «высокий» профессионал, личность приятная во всех отношениях, но без особой склонности к руководству). В этом случае приоритеты могут быть установлены, например, на следующих значениях: для профессиональных качеств ¾ kп1=1.15, личностных ¾ kп2 =1.05, деловых ¾ kп3 =0.8. Значения весовых коэффициентов для групп качеств r определяются формулой:

(ar)i = kпr / n,     где  n = 9,  r= 1, 2, 3,

и равны – (a1)i =

1.15 / 9 = 0.128; (a2)i =  1.05 / 9 = 0.117; (a3)i =  0.8 / 9 = 0.089.

Вектор-строка весовых коэффициентов имеет вид:

i		1		2		3		4		5		6		7		8		9
(ar)I		(a1)i		(a1)i		(a1)i		(a2)i		(a2)i		(a2)i		(a3)i		(a3)i		(a3)i

Средневзвешенная оценка качества менеджера  в баллах (пункт 8 на рис. 4.17) ¾

Kм

= 4.496.

Итак, в рассмотренном примере в зависимости от способа определения весовых коэффициентов получены три оценки качества:

Km = 4.162 – при экспертной оценке a;

K1m

= 4.593 – случай равнозначимых весовых коэффициентов;

K2m = 4.496 – при приоритете (kп1=1.15) профессиональных качеств.

Выбор кандидата – прерогатива лица, принимающего решение, или конкурсной комиссии.

Рассмотренная методика применима для оценки качества продукции, результатов испытаний, экзаменов и других задач экспертной оценки.

Возможно, руководителю группы экспертов или заказчику экспертизы потребуется анализ результатов работы экспертов для оценки их компетентности, пристрастий или добросовестности.

Весовые коэффициенты i-го качества в оценке j-го эксперта рассчитываются по формуле



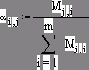
Результаты расчета содержатся в матрице a (пункт 5 на рис. 4.17).

Для наглядного представления результатов работы экспертов, анализа оценок, близости объекта к эталону качества в некоторых задачах очень удобна радарная диаграмма (Radar-diagram). Пример – экспертиза проекта электростанции по таким показателям: экономичность, экологичность, архитектурные решения, совместимость с еще не подпорченным ландшафтом, безопасность, надежность, значимость для экономики региона и др. Для всех показателей из центра диаграммы проводятся лучи, на которых откладываются средние значения оценок экспертов. Соединив точки на лучах, получим многоугольник. Эталону качества будет соответствовать вписанный в окружность с радиусом М (М – высший балл по шкале оценок) правильный многоугольник[17]. Степень приближения к эталону наглядно представляется формой и относительной площадью получившегося на основе оценок экспертов многоугольника (пункт 2 на рис. 4.6).

Тема оценки качества далеко не исчерпана. Интересные решения могут быть получены с использованием теории нечетких множеств (см. этюд 6).

[1] Сравните пары римских и арабских чисел на рис. 6.47.

[2] В среде Mathcad при форматировании чисел допустимо менять систему счислений. Двоичная система появилась только в Mathcad 8.

[3] Для поддержки АСНИ существуют также и специализированные программные средства – LabVIEW, LabWindows (разработка National Instruments, Corp.), например.

[4] Здесь лучше записать не нуль, а системную (предопределенную) переменную ORIGIN. Так мы и поступим в пункте 3.2 на рис. 4.2.

[5] Здесь чаще используют термин «аппроксимация» – приближение прямой линии к точкам. Еще здесь упоминают регрессию

– зависимость средней величины (прямая линия) от других величин (экспериментальные точки). Тут можно усмотреть некую путаницу в терминологии. Надеемся, что читатель в данном случае сам разберется, что к чему.

[6] Третья группа инструментов решения задач – это команды меню.



[7] Градация на линейную и нелинейную аппроксимацию весьма условна.

[8] Вот здесь-то и пригодятся средства символьной математики (этюд 7).

[9] На него нужно предварительно поместить курсор.

[10] Студенты автора называют ее «тормозная бабушка».

[11] Операторы функции, формируемых на рис. 4.10 и 4.13, объединены в единый операторный блок. Это позволяет использовать механизм локальных переменных – см. этюд 6.

[12] Автор советов – преподаватель Московского энергетического института. Основа не только российской, но и мировой энергетики – это теплоэнергетика (ТЭС и АЭС), где рабочее тело – в основном, вода и водяной пар.

[13] Если создаваемая функция будет использоваться для решения обратной задачи (поиск, например, значения температуры при заданных значениях давления и энтальпии пара), то такие сообщения об ошибке лучше убрать. При численном поиске корня уравнения (а к этому сводится такая задача) ничего не будет страшного в том, что мы временно будем вылезать из области разумного существования аргументов.

[14] Главка написана совместно с М.Панько.

[15] Понятие «эталон качества»- синоним оценки «высочайшее качество».

[16] Существенный недостаток данной методики в том, что все эксперты обязаны оценить все без исключения качества испытуемого. Мы должны заполнить прямоугольную таблицу – матрицу. Но в реальной жизни далеко не все привлеченные к этой работе являются признанными экспертами в оценке всех качеств объекта исследования. Мы уже сталкивались с подобной проблемой, втискивая табличные данные по энтальпии пара в квадратную матрицу – см. рис. 4.10.

[17] Вспомним чеховское: «В человеке все должно быть прекрасно – и лицо, и одежда, и душа, и мысли!»

Задача об эпидемии – разностная схема

Все это словесное описание модели эпидемии легко вмещается в Mathcad-документ (рис. 5.1) с двумя формулами (пункт 2), объединенными в вектор, что эквивалентно BASIC-конструкции:

For t = 1 To 13

            Больные(t + 1) = Пр * Больные(t) * Здоровые(t)

            Здоровые(t + 1) = Здоровые(t) - Больные(t)

Next

Если бы два выражения в пункте 2 на рис. 5.1 не были заключены в скобки, то их выполнение сразу бы прерывалось сообщением об ошибке. Система Mathcad пыталась бы сначала полностью заполнить вектор Больные, а уже потом – вектор Здоровые. Скобки изменяют порядок счета: он ведется не по строкам, а по столбцам: сначала заполняются вторые элементы векторов Больные и Здоровые (первые элементы заполняются в пункте 1 – начальные условия), а потом третьи и т.д. Этими скобками мы меняем естественный порядок выполнения операторов[1]

¾ они выполняются не слева направо и не сверху вниз, а крест накрест.

Результаты расчета графически отображены[2]

в пункте 3. На тринадцатый день (спад эпидемии) в городе было 105 больных. Критическая точка – девятый день (3972 больных), ради поиска которой и затевают весь этот расчетный сыр-бор: моделируя эпидемию, мы можем распланировать работу санитарных служб города – подвезти в аптеки лекарства, отозвать врачей из отпуска, выписать из больниц выздоравливающих и т.д. В оригинальном решении задачи дополнительно прослеживается динамика изменения числа умерших во время эпидемии. Но мы исключим эту печальную кривую. Тем более что она и математически не вписывается в задачу: динамика числа умерших просчитывается отдельно от динамики больных и здоровых.

Задача об эпидемии – решение системы дифференциальных уравнений

В пункте 5 рис. 5.2 столбцы матрицы Z (время, число больных и число здоровых) разнесены по отдельным векторам и отображены графически, что позволяет проследить динамику развития эпидемии.

На рис. 5.2 получены несколько иные результаты, чем на рис. 5.1, хотя характер кривых сохранился: максимум больных (3119) наблюдается не на 9-й, а на 7-й день, на 13-й день мы имеем не 105, а 209 больных. Это объясняется и различными значениями точности расчетов (на рис. 5.1 делалось 13 шагов интегрирования, а на рис 5.2 ¾ 500) и различными примененными методиками (Эйлер против Рунге и Кутта[5]).

В функцию rkfixed заложен широко распространенный метод решения дифференциальных уравнений – метод Рунге ¾ Кутта[6]. Несмотря на то что это не самый быстрый метод, функция rkfixed почти всегда справляется с поставленной задачей. Однако есть случаи, когда лучше использовать более сложные методы. Эти случаи попадают под три широкие категории: система может быть жесткой[7]

(Stiffb, Stiffr), функции системы могут быть гладкими

(Bulstoer) или плавными (Rkadapt). Нередко приходится пробовать на одном дифференциальном уравнении (одной системе) несколько методов, чтобы определить, какой метод лучше (быстрее, точнее). Примерно так мы сравнивали в этюде 3 разные способы поиска оптимумов функции.

Когда известно, что решение гладкое, используется функция Bulstoer, куда заложен метод Булирша ¾ Штёра, а не Рунге ¾ Кутты, используемый функцией rkfixed. В этом случае решение будет точнее. Список аргументов и матрица, получаемая при работе с функцией Bulstoer, такие же, как и при работе с rkfixed.

Можно решить задачу более точно (более быстро), если уменьшать шаг (у нас это Dt) там, где производная меняется быстро, и увеличивать шаг там, где она ведет себя более спокойно. Для этого предусмотрена функция Rkadapt (adaption –адаптация). Но, несмотря на то что при решении дифференциального уравнения функция Rkadapt использует непостоянный шаг, она тем не менее представит ответ для точек, находящихся на одинаковом расстоянии, заданном пользователем. Аргументы и матрица, возвращаемая функцией Rkadapt, такие же, как при rkfixed.

При решении жестких систем следует использовать одну из двух встроенных функций, разработанных специально для таких случаев: Stiffb и Stiffr.
Они используют метод Булирша ¾ Штёра (b) или Розенброка (r). Форма матрицы-решения, полученной с помощью этих функций, идентична матрице, полученной через rkfixed. Однако Stiffb и Stiffr требуют дополнительного аргумента J:
Stiffb(x, tнач, tкон, n, f, J)
Stiffr(x, tнач, tкон, n, f, J),
где
x – вектор n начальных значений;
 tнач, tкон – конечные точки интервала, в котором должно быть найдено решение дифференциальных уравнений. Начальные значения x определяются в точке tнач;
n – количество точек за начальной точкой, в которых должно быть определено решение. Это определяет число рядов (1 + n) матрицы, которую генерируют функции Stiffb и Stiffr;
f(t, x) – функция-вектор правых частей системы;
J(t, x) – матрица-функция размерности n×(n+1), в которой содержится матрица Якоби правых частей дифференциальных уравнений.
В функциях для решения дифференциальных уравнений, описанных ранее, предполагалось, что необходимо получить таблицу значений x(t) относительно значений t, расположенных на одинаковом расстоянии друг от друга на отрезке интегрирования, ограниченном точками tнач и tкон. Но часто требуется найти решение только в конечной точке tкон. Хотя описанные функции определяют значение x(tкон), они проделывают при этом много ненужной работы, высчитывая промежуточные значения x(t).
Если необходимо узнать только значение x(tкон), используются следующие функции:
bulstoer( x, tнач, tкон, acc, f, kmax, save)
rkadapt( x, tнач, tкон, acc, f, kmax, save)
stiffb( x, tнач, tкон, acc, f, J, kmax, save)
stiffr ( x, tнач, tкон, acc, f, J, kmax, save),
где
x – см. выше;
tнач, tкон – конечные точки интервала, на котором должно быть найдено решение дифференциальных уравнений. Начальные значения t определяются в точке tнач;
acc – контролирует точность решения. При небольших значениях acc делаются более мелкие шаги вдоль траектории, что увеличивает точность решения;


f(t, x) – см. выше;
J(t, x) – см. выше;
kmax – максимальное количество промежуточных точек, в которых будет найдено решение. Значение kmax устанавливает верхнюю границу количества рядов матрицы, получаемой этими функциями;
save – наименьшее допустимое расстояние между величинами, в которых должно быть найдено решение. Значение save устанавливает нижнюю границу разницы между любыми двумя числами в первой колонке матрицы решения.
Вернемся к нашему примеру с эпидемией. Если известно начальное число больных (N=50 – см. пункт 1 на рис. 5.1), то это значит, что их сразу пересчитали. А если это так, то их знают поименно. Но в этом случае больные должны быть изолированы, и никакой эпидемии не будет вообще (Пр=0). В реальной задаче мы можем знать число жителей в городе (число здоровых на день начала эпидемии) и число больных в какой-то последующий день, когда становится ясно, что разразилась эпидемия. Другими словами, нам что-то известно о параметрах на краях отрезка, охватывающего некий динамический процесс.
На рис. 5.3. реализован метод последовательных приближений для решения по разностной схеме такой краевой задачи: в начале эпидемии в городе 20 000 здоровых жителей, а в конце эпидемии – 100 больных. Спрашивается, сколько больных было в начале эпидемии.

Решение краевой задачи об эпидемии разностной схемой

Ответ (51 больной) получен за семь приемов: задается начальное число больных, которое корректируется в зависимости от того, какое число больных оказывается в конце эпидемии. На рис. 5.3 можно, конечно, не дублировать Mathcad-оператры, а просто вручную подправлять первое приближение.

С помощью функций Bustoer, bustoer, Rkadapt, rkadapt, rkfixed, Stiffb, stiffb, Stiffr и stiffr, решающих задачу Коши, краевую задачу можно также решить последовательными приближениями (см. рис. 5.4 с функцией rkfixed):

---

---