Решение краевой задачи об эпидемии функцией rkfixed
Нижняя кривая на рис. 5.2 похожа на траекторию полета снаряда[8], поэтому метод последовательных приближений, приложенный к краевой задаче, называют также методом стрельбы: можно менять искомые начальные условия, последовательно приближаясь к решению, имея на другом конце отрезка «корректировщика огня», в лексиконе которого три слова: «перелет», «недолет» и «попал» («почти попал», учитывая заданную точность расчета – см. комментарии на рис. 5.3). По правде говоря, метод стрельбы берет свое название не от вида кривой, а от особенностей решения краевой задачи применительно к дифференциальному уравнению второго порядка, когда приходится менять угол наклона ствола пушки – значение первой производной на конце отрезка интегрирования. В нашей задаче об эпидемии (система двух обыкновенных дифференциальных уравнений) для попадания в цель приходится менять не угол наклона пушки, а ее подъем над землей – число больных в начале эпидемии. Тут, как правило, используют метод половинного деления, когда отрезок «перелет-недолет» делят пополам.
Решение краевой задачи об эпидемии функцией sbval
Метод стрельбы заложен и во встроенную функцию sbval, работа которой показана на рис. 5.5. Она требует начального приближения и соблюдения некоторых условностей, связанных с нашими знаниями состояний решаемой системы на концах отрезка интегрирования. Функция sbval не совсем обычная. Мы привыкли к тому, что, например, операторы A:=sin(X) и A:=sin(30) идентичны, если переменная X имеет значение 30, несмотря на то, что в первом случае у функции sin в качестве аргумента выступает переменная, а во втором – константа. Функция же sbval в этом отношении аномальна. Она возвращает значение в зависимости не только от конкретных значений аргументов, но и от того, введены они в виде переменных (x0) или в виде констант (20 000). Из-за этого даже специалистам по дифференциальным уравнениям часто приходится ломать голову, чтобы сообразить, как можно условия краевой задачи «запихнуть» в функцию sbval. Здесь фирма MathSoft несколько отошла от первоначальной идеологии пакета Mathcad, подразумевавшей, что запись условия задачи на экране дисплея должна выглядеть естественно.
Типичный пример – численное решение в среде Mathcad системы алгебраических уравнений: сначала задается начальное приближение к корню (ведь корней может быть много), потом за ключевым словом Given (дано) в естественном виде пишется сама система уравнений, после которой помещается функция Find, возвращающая значения своих аргументов, превращающих ранее записанные уравнения (до слова Given) в тождества. Функция Find также аномальна: она возвращает значения, зависящие не только от значений аргументов, но и от того, что вблизи нее находится. Это, конечно, грубейшее нарушение правил построения функциональных зависимостей. Но разработчикам Mathcad пришлось пойти на это ради того, чтобы алгебраические уравнения в Mathcad-документе хранились в естественной форме. При создании математических пакетов типа Mathcad приходится решать не только чисто математические проблемы (разработка алгоритмов решения и реализация их средствами вычислительной математики), но и проблемы единства формы представления задачи (интерфейс пользователя) и методов ее решения.
Функция sbval не решает краевую задачу, а только находит недостающие значения на краю отрезка. После этого краевая задача переходит в задачу с начальными условиями (задача Коши), которая и решается в пункте 7 рис. 5.5. Заодно проверяется точность решения: задали 100 больных – получим почти 100 (ошибка во втором знаке после запятой).
Для решения краевой задачи в среде Mathcad есть еще одна функция – bvalfit. Она используется в тех случаях, когда нет всей необходимой информации для функции sbval, но известно решение задачи в промежуточной точке. Функция bvalfit решает задачу с двумя граничными точками, начиная с конечных точек и следуя траекториям решения и его производным в промежуточных точках:
bvalfit( x1, x2, tнач, tкон, tf, f, load1, load2, score),
где
x1- вектор предполагаемых начальных значений, не определенных в точке х1;
x2 – то же для точки х2;
tнач, tкон – конечные точки интервала, в котором должно быть вычислено решение дифференциального уравнения;
tf – точка между tнач и tкон, в которой траектории решений, начатые с tнач, и траектории, начатые с tкон, должны совпадать;
f(t, x) – векторная функция, состоящая из n элементов, содержащая первые производные неизвестной функции;
load1(tнач, x1) – векторная функция, n элементов которой соответствуют значениям n неизвестных функций в точке х1. Некоторые из этих значений будут постоянными, заданными начальными условиями. Другие будут неизвестны вначале, но будут найдены. Если значение неизвестно, то следует использовать соответствующее предполагаемое значение из вектора x1;
load2(tкон, x2) – аналог load1, но для значений n неизвестных функций в точке х2;
score(tf, x) – векторная функция, состоящая из n элементов. Эта функция применяется для того, чтобы задать, как решения должны совпадать в точке tf. Обычно нужно определить score(tf, x):= x, чтобы все решения неизвестных функций совпадали в точке tf.
Функция bvalfit по своей сути решает две краевые задачи на двух смежных отрезках интегрирования. Она особенно полезна, когда производная имеет разрыв где-то внутри интервала интегрирования. При развитии эпидемии (наша задача) такое может произойти, если, например, комиссия из центра снимет с работы медицинское начальство города и тем самым изменит значение коэффициента Пр.
Второй тип задач с граничными условиями появляется при решении дифференциального уравнения с частными производными. В этом случае приходится фиксировать значение решения не в двух точках, как было сделано в предыдущей «плоской» задаче, а в совокупности точек, составляющих границу: в углах прямоугольника, например. В среде Mathcad имеются две функции (relax и multigird) для решения таких уравнений. Но разговор о них выходит за рамки этой книги. Скажем лишь то, что эти функции предназначены для решения дифференциальных уравнений конкретного вида – уравнений Лагранжа и Пуассона. Задачи другого вида требуют составления индивидуальной схемы решения с привлечением той же «плоской» функции rkfixed.
Моделирование развития финансовой пирамиды
В пункте 1 рис. 5.6 вышеприведенного протокола работы в среде Mathcad определяются константы – ее имя, знак присвоения (:=) и величина. Комментарии расшифровывают их.
В пункте 2 определяется состояние пирамиды на первый день: вводятся индексные переменные – первые значения векторов M, NK и MMM.
В пункте 3 записана динамика изменения курсов продажи и покупки акций – функции P(t) и K(t): объявляется о выпуске акций (билетов) номиналом в 100 рублей со следующим курсом продажи P и покупки K:
Таблица 5.1
| Число дней, прошедших с начала эмиссии акций (билетов) | 1 | 2 | 3 | ... | 51 | ... | 365 | ... | |||||||||
| Продажа (руб.) | 105 | 107 | 109 | ... | 205 | ... | 833 | ... | |||||||||
| Покупка (руб.) | 100 | 102 | 104 | ... | 200 | ... | 828 | ... |
Из таблицы 5.1 видно, что купленная акция может дать дивиденд в 723% годовых при номинальной своей цене в 100 рублей. Если уровень инфляции достаточно высок, то люди верят в реальность таких огромных дивидендов и пирамида растет. Но опасность краха этой затеи ощущают почти все и отдают свои деньги не на год, а, допустим, на 50 дней (переменная Время – среднее время между покупкой и продажей акций – см. пункт 1). За этот период по каждой акции можно «наварить» магические 100 рублей, фигурирующие во многих пословицах и поговорках.
Далее векторы NK и NP заполняются по простой разностной схеме: известно предыдущее значение элемента вектора (на день t) – рассчитывается его очередное значение (на день t+1).
В городе, где строится пирамида, миллион жителей (N – см. пункт 1), среди которых царит некий ажиотаж, подогреваемый вышеприведенной таблицей курсов. Языком математики его можно описать формулой, связывающей число проданных населению акций в конкретный день (NK) с общим числом проданных акций (сумма NK за предыдущие дни) и условным числом жителей, не купивших пока акции (N минус сумма NK за предыдущие дни). Повторяем, развитие финансовой пирамиды во многом напоминает развитие эпидемии, когда число заболевших (купивших акции) в конкретный день пропорционально числу больных в городе (числу проданных акций), перемноженному на число еще не переболевших (не купивших акции). В случае эпидемии коэффициент пропорциональности зависит от мер профилактики. В случае финансовой пирамиды этот коэффициент (мы его условно назовем коэффициентом ажиотажа – KA) зависит от уровня инфляции, рекламы (вспомним Марину Сергеевну, Леню Голубкова и прочих «бабочек»), наличия других параллельных пирамид, от срока, прошедшего с момента шумного краха предыдущей пирамиды, и т.д. Многие экономические явления (кризисы, банкротства) прокатываются волнами. Период пика волн финансовых пирамид составляет, по различным оценкам, от 25 до 30 лет, что связано, во-первых, с приходом к активной жизни свежих, незатронутых пирамидами сил, и, во-вторых, с короткой людской памятью. На таких волнах многих ждет финансовое кораблекрушение. Другие же (а их намного меньше – и в этом фокус пирамид), подобно отважному и ловкому серфингисту, получают «финансовое» удовлетворение.
За волной купивших акции «катит» волна желающих их продать – вернуть свои «кровные» и причитающиеся дивиденды. Здесь мы также до предела упростим модель и будем считать, что волна продающих акции отстает от волны их купивших на число дней, хранящихся в переменной Время:
NPt+1 = 0, если t £ Время
NPt+1 = NKt-Время, если t > Время.
Волны покупателей и продавцов акций могут иметь разные формы – подчиняться, например, нормальному закону распределения (см. в этюде 6 рис. 6. 41 в этюде 6). Главное здесь раздвоенность волн: человек сначала покупает акцию (билет) и только потом ее продает.
Ну а теперь можно подсчитывать барыши и кататься на волнах финансовой пирамиды.
Развитие финансовой пирамиды
Несложно вычислить, сколько денег (вектор M ¾ см. пункт 5 на рис. 5.7) будет на счету организаторов пирамиды завтра (t + 1), если известно, сколько их в наличии сегодня (t), и если известен курс акций и количество покупок и продаж:
Mt+1 = Mt + NKt × K(t) - NPt × P(t)
Люди, покупающие акции, приносят деньги в кассу. Люди, акции сдающие, забирают деньги из кассы. Но есть еще один человек, залезающий в кассу. Это – организатор пирамиды, имеющий свой «профит», что выражается в том, что из кассы ежедневно изымаются три процента (Доход := 0.03 – см. пункт 1) наличных денег:
Доход × Mt
Естественно, доход изымается, если (if) в кассе есть деньги. В реальной жизни, конечно, касса худеет на значительно большие суммы – налоги, оплата текущих расходов, реклама и т.д. Расход := 300 000 – см. пункт 1.
В 1202 году Леонардо Пизанский (1180-1240) описал одну из первых моделей развития замкнутой биологической системы, населенной условными кроликами. Если соответствующим образом определить их плодовитость и долголетие, то численность популяции кроликов будет меняться из поколения в поколение по строгому закону:
Таблица 5.2
| Поколение | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... | 27 | ... | |||||||||||
| Число кроликов | 1 | 1 | 2 | 3 | 5 | 8 | 13 | ... | 196 418 | ... |
Читатель, конечно, уже догадался, что речь идет о числах Фибоначчи: Леонардо Пизанский более известен под именем Фибоначчи (Fibonacci – сокращение от filius Bonacci – сын Боначчи). В новом поколении кроликов их число будет равно сумме числа кроликов в двух предыдущих поколениях (см. программу на рис. 6.11 в этюде 6). Со временем про этих условных кроликов забыли, но числа Фибоначчи (1, 1, 2, 5, 8, 13 и т.д.) нашли применение в прикладной математике (см. этюд 6).
Наша модель развития пирамиды также позволяет сгенерировать некий числовой ряд, отображающий состояние дохода организаторов этой финансовой операции (вектор МММ):
Таблица 5.3
| День | Доход (округлено до рублей) | Примечание | |||
| 1 | 70 000 000 | Начало пирамиды | |||
| 2 | 72 100 000 | ||||
| 3 | 74 128 022 | ||||
| 4 | 76 086 206 | ||||
| ... | ... | ||||
| 168 | 303 058 831 | ||||
| 169 | 303 485 168 | ||||
| 170 | 303 635 916 | День икс | |||
| 171 | 303 635 916 | ||||
| 272 | 303 635 916 | ||||
| ... | ... |
/p> Назовем числа второго столбца таблицы 5.3 числами Мавроди[11]. Будем надеяться, что со временем о финансовых пирамидах забудут, но числа Мавроди войдут в историю. Тем более, что сам Сергей Мавроди по образованию математик.
В пунктах 5-6 графически отображено развитие пирамиды. Просматривая матрицу M, можно определить «день икс», когда прибыль организатора достигает максимума (у нас это 170-й день – см. пункт 7), и когда пирамиду пора разваливать – уходить на «дно», баллотироваться в депутаты или уезжать за границу. Благо денег на это «наварено» достаточно – почти триста миллионов при всего лишь трехпроцентной норме прибыли.
Мы же никуда пока не уезжаем, остаемся у своего компьютера и, собираясь вкладывать деньги в какое-то надежное или сомнительное предприятие, сначала должны просчитать, что из этого может выйти. Так мы легко можем вернуть и приумножить деньги, потраченные на приобретение компьютера и программы Mathcad[12], а также на операционные системы Windows, под управлением которой Mathcad работает.
Кроме того, читатель должен не забывать о задании, которое он получил, – решить задачу о финансовой пирамиде не по разностной схеме, а через дифференциальные уравнения.
[1] Об этом атрибуте программирования будет подробнее сказано в этюде 6.
[2] Здесь используются два типа декартова графика: линия с точками в виде квадратиков и так называемая bar-diagram – плоская столбчатая диаграмма.
[3] Или Ойлера – что в него заложено, можно увидеть в этюде 6 на рис. 6.3.
[4] Здесь лучше написать Тнач и Ткон, опустив индекс.
[5] Многие математики полагают, что есть только один метод Эйлера. Все остальное ¾ модификации этого метода.
[6] Или Рунге – Кутты, что в него заложено – см. рис. 6.3 в этюде 6.
[7] Термин «жесткий» происходит из механики, где численное решение некоторых систем дифференциальных уравнений требует разного шага интегрирования по разным искомым функциям.
[8] Она может быть совсем не похожа на траекторию полета снаряда, но… читаем дальше.
[9] В этюде 6 мы рассмотрим методику составления одной функции для такого рода расчетов, возвращающую сумму налога.
[10] Некоторые банки Великобритании предлагают своим клиентам такие условия: процент по вкладку равен уровню инфляции плюс 1-2%.
[11] Или числами ГКО, если вспомнить 17 августа 1998 г.
[12] См. в конце книги информацию о фирме СофтЛайн, официальном представителе MathSoft на российском рынке (рекламная пауза!).
Поиск корня алгебраического
Кроме «зашифрованности» алгоритма (чего стóят аргументы функции until на рис. 6.1) «беспрограммный» поиск корня имеет и другой недостаток: он приводит к нерациональному использованию ресурсов компьютера – к генерации векторов a и b, у которых нас интересуют только последние (last) элементы: между ними зажат искомый корень (переменная корень)[3].
Операторы if и until позволяют менять естественный порядок выполнения операторов в Mathcad-документе: сверху вниз и слева направо. Кроме того, есть еще два признака программирования: локальные переменные и объединение операторов в операторные блоки.
Путь 2. Версии Mathcad начиная с 4.0 – это полноценные Windows-приложения. При решении конкретной задачи в среде Mathcad можно в статике (через файлы на диске или через Буфер обмена – Clipboard) или в динамике (технология DDE и OLE) перенести данные (скаляр, вектор или матрицу) в среду, например, fortran’а и, используя богатый набор средств вычислительной математики этого языка, решить задачу (этап задачи). В среде Mathcad 7 Pro и 8 Pro эта технология была развита и визуализирована через инструментарий MathConnex (см. приложение 10).
Путь 3. Начиная с пятой версии Mathcad пользователям была предоставлена возможность программирования на языке С и объявления в среде Mathcad новых встроенных функций (операторов). Код этих функций нужно откомпилировать каким-либо 32-разрядным транслятором и прикрепить к среде Mathcad через механизм DLL. Но этот путь с самого начала был тупиковым. Во-первых, Mathcad создавался как инструмент решения широкого класса задач теми, кто не хотел или не умел возиться с классическими языками программирования. При обращении же к языку C получалось, что от чего ушли, к тому и пришли. Во-вторых, тот, кто все-таки переключался из среды Mathcad в среду языка С, как правило, там и оставался, решая всю задачу целиком. В-третьих (вернее, во-вторых с половиной), если кто-то и мог решить свою задачу на языке С, то он обычно не пользовался услугами Mathcad по моральным соображениям, считая это ниже своего достоинства. Но главным недостатком в технологии использования C для расширения возможностей Mathcad является невозможность включения в C-программу богатого математического инструментария Mathcad. Технология написания С-функций описана в приложении 8.
Панель программирования Mathcad
Щелчок по одной из этих кнопок создает на дисплее заготовку соответствующей программной конструкции.
Опишем их.
Кнопка

Было

стало

Вертикальная линия объединяет отдельные операторы в операторный блок с одним входом и одним выходом, который выполняется как единый оператор (один из трех атрибутов структурного программирования). Какое-то подобие операторного блока пользователь Mathcad часто выделяет и в беспрограммном документе, реализуя, например, метод последовательных приближений (см. пункт 6 на рис. 5.1).
Кнопка

A := A := B + C (Pascal),
А = А = В + С (BASIC)[7].
В Mathcad-выражении:
A := A ¬ B + C
все более-менее ясно: локальной переменной A (она в середине между символами «:=» и «¬») присваивается значение суммы двух переменных B и C, значение которых уже задано выше в Mathcad-документе (глобальные переменные). Затем эта сумма передается глобальной переменной A (она слева от знака «:=»).
Простейший пример, показывающий разницу между глобальной и локальной переменной:

Негативное изображение переменной В будет свидетельствовать о том, что ее значение вне программы (В ¬ 3) неопределенно[8]. Благодаря локальным переменным можно создавать объемные Mathcad-документы, поручая разработку отдельных функций и операторов разным программистам и не заботясь о разделении переменных: в разных программах переменные могут совпадать по имени, но при этом они не будут перебегать дорогу друг другу (технология программирования «сверху вниз»). С локальными переменными мы, кстати, сталкивались и ранее: примеры индексы i, j и др. в операторах суммы или произведения (см., например, конец рис. 3.14).
Итак, локальная переменная распространяет свое действие только на программу, а глобальная – на весь документ (на низ документа). Но в среде Mathcad есть инструментарий, позволяющий переменным, пользовательским функциям и операторам проникать и в другие документы, но с их, так сказать, согласия. Представим такую ситуацию. Конкретный пользователь создал функции, которые помогают ему быстро решать задачи в конкретной научно-технической области. Решая очередную задачу, пользователь должен в начале документа записать все нужные для расчета функции. Среда Mathcad предоставляет пользователю и другое решение данной проблемы. В новом документе можно сделать ссылку (Reference) на документ (файл с расширением *.mcd), хранящий нужные пользовательские функции, операторы и переменные. Документ, на который ссылаются, может в данный момент не быть открытым, а просто храниться на диске. После этого к создаваемому документу как бы приписывается сверху еще один документ. Пример ссылки на другой Mathcad-документ можно видеть на рис. 6.29, 6.30 и 6.49.
Нажав на кнопку

с предпроверкой – слово while с двумя пустыми квадратиками:

В первый квадратик (правее while) нужно будет записать булево выражение (переменную), управляющее циклом, а во второй (ниже while) – тело цикла, операторы которого будут выполняться, пока булево выражение возвращает значение «Да» (в среде Mathcad – это числовое значение, отличное от нуля). Если в теле цикла более одного оператора (а это основное отличие оператора while от вышеупомянутой функции until), то нужно воспользоваться кнопкой Add Line (см. выше).
Численное решение задачи Коши (иллюстрация цикла while)
На рис. 6.3 представлены программы численного решения дифференциального уравнения методом Эйлера и методом Рунге ¾ Кутты 4-го порядка. Ядро программ – цикл while. Созданные программно функции Euler и RK4 возвращают значение (в случае системы уравнений – вектор значений) неизвестного выражения, являющегося решением обыкновенного дифференциального уравнения (системы). Аргументы функций Euler и RK4: х1 – значение (вектор значений в случае системы) искомого выражения в начале отрезка интегрирования (решается задача Коши), t1 и t2 – интервал интегрирования, n – число шагов интегрирования и f – правая часть дифференциального уравнения (в случае системы f – вектор-выражение). Функции Euler и RK4 протестированы на расчете числа е (численное решение задачи Коши для дифференциального уравнения х’ = х) и на задаче об эпидемии, которая нами уже была решена встроенными средствами Mathcad (см. рис. 5.2) функцией rkfixed. Программой же на рис. 6.3 мы как бы раскрываем алгоритм работы функции rkfixed. Читатель может доработать функции Euler и RK4 так, чтобы они возвращали решение не только в конечной точке интегрирования, но и на всем интервале интегрирования. Так работает встроенная функция rkfixed.
В программах на рис. 6.3 записаны комментарии – названия функций. Mathcad, к сожалению, не имеет стандартных средств комментирования программ, поэтому мы поступили так – записали в текст программы текстовую константу “Метод Эйлера” и “Метод Рунге ¾ Кутты 4-го порядка”. Комментарии в тексте программ компилятором игнорируются[10], но они помогают читающему программу понять, что здесь имелось в виду, почему тут был использован данный оператор, а не другой и т.д. В программе без комментариев через некоторое время не сможет разобраться (а тем более подправить или развить ее) даже автор.
Кнопка

if A > B then C := D
в среде Mathcad будет выглядеть несколько по-арабски (по-еврейски – записана справа налево):
С ¬ D if A > B.
Но если плечо альтернативы – составной оператор, то все встанет на свои места, вернее, будет записано по-китайски (сверху вниз):
Pascal:
if A>B then begin E:=F; F:=G end[11];
Mathcad:
|
if A>B |
|
E¬F F¬G |

|
Pascal: |
if A > B then C := D else E := F; |
|
Mathcad: |
C ¬ D if A > B |
|
E ¬ F otherwise |
C¬if(A > B, D, F) или if(A > B, C¬D, E¬F)
Понять, почему в Mathcad не было использовано традиционное слово else, можно, если принять во внимание то, что операторы if и otherwise позволяют записать в программах алгоритмическую конструкцию множественное ветвление. Разберем ее на примере задачи о расчете налогов (федеральный налог США с недельного заработка).
Налоги США (иллюстрация конструкции «выбор»)
Функции Tax1 и Tax2 (пункт 1) возвращают налог с холостых и женатых по прогрессивной шкале налогообложения (см. график в пункте 3). В данном примере (и во всех других) без оператора otherwise можно обойтись (сравните окончания функций Tax1 и Tax2). Он необходим в тех случаях, когда булево выражение, объединяющее оставшиеся случаи ветвления, трудно сформировать. Оператор otherwise – это гибрид ключевых слов ELSE, ELSEIF и CASE ELSE языка BASIC.
Программы на рис. 6.4 несложно реализовать и без программирования (без операторов if и otherwise), задействовав традиционную Mathcad-функцию if и вкладывая ее саму в себя: if(..., if (..., if(... и т.д. Но программирование функций Tax1 и Tax2 делает их более прозрачными и для понимания, и для редактирования.
В седьмой версии Mathcad появился оператор досрочного прерывания программы, который вводится нажатием кнопки return. Он очень уместен в программе на рис. 6.4 (см. пункт 2): если налогоплательщик мало получает и тем самым освобожден от налога, то нечего и забираться в глубь программы. Кроме того, программой в пункте 2 на рис. 6.4 проиллюстрирована работа текстовой переменной (у нас это S), а также функции error выдачи пользовательского сообщения об ошибке: если к «покрасневшей» функции Tax (последняя строка в пункте 2) подвести курсор, то «выпадет» пользовательское сообщение об ошибке “Укажите правильный статус налогоплательщика”. Дополнительно в функцию Tax на рис. 6.4 введены денежные единицы по принципу «Время – деньги» – см. рис. 1.14.
В программах на рис. 6.4 можно заменить константы и получить функцию для расчета российских налогов. Автор этого не делает по следующим причинам.
Во-первых, за нашей шкалой налогообложения не угнаться. Инфляция с деноминацией и с новой инфляцией делает бессмысленными коэффициенты формул. Кроме того, наши парламентарии считают, что у нас налоги не собираются из-за плохой налоговой системы, в частности, из-за неправильных коэффициентов функции Tax. Но это иллюзии. Налоги у нас не платят в первую очередь из-за того, что люди не хотят отдавать свои деньги неизвестно на что[12]. На больницы, на школы денег нет, а губернатор N-ской области, где эти бедные школы и больницы расположены, еженедельно на своем личном самолете со своей многочисленной свитой летает в Москву. Когда ему говорят, что так делать нельзя, что бюджетные средства в первую очередь должны идти в социальную сферу, то он эти законные претензии называет «дешевым популизмом». Сами же налогоплательщики не желают иметь в качестве посредников таких нечестных людей и стараются отдавать деньги бюджетникам напрямую – собирают деньги на уборку класса, передают конверт с «благодарностью» врачу и т.д. Конечно, это порочная система, но что делать, если люди, призванные распоряжаться нашими деньгами, не могут или не хотят сделать это умно и честно.
Сравнивая нашу шкалу налогов с американской, следует отметить, что в США при больших заработках ставка налога падает с 33 до 28%. Дальновидная политика! В стабильном обществе богатые люди свои доходы не прячут и не проедают, а пускают в дело – расширяют производство, покупают акции и т.д. Кроме того, американская налоговая система нацелена на укрепление семьи. Но мы отвлеклись от основной темы…
Кнопка

Когда заранее известно, сколько раз нужно выполнить какую-то часть программы (тело цикла), то используют не цикл while, а цикл for, в заголовке которого пишут не булево выражение, а параметр цикла и указывают, какие дискретные значения он должен принимать в цикле. Эти значения можно перечислить через запятую (1, 2, 3.7) или указать диапазоном (2.. 100) или вектором (V). В программах на рис. 6.3, кстати, более уместен цикл for с заголовком for t Î t1, t1 +D.. t2, а не цикл while. При этом программы можно будет несколько упростить, убрав операторы t ¬ t1 и t ¬ t + D (см. рис. 6.5).
Решение буквенной головоломки USA+USSR=PEACE (иллюстрация цикла с параметром)
Программа на рис. 6.6 решает буквенную головоломку USA+USSR=PEACE, где требуется указать, какие цифры скрываются за буквами. В программе три цикла с параметром (A, C и S), которые вложены друг в друга. В программе, не мудрствуя лукаво, можно было записать все семь циклов – по числу неизвестных задачи U, S, A, R, P, E и C. Но тогда перебор (а именно этим способом решается наша головоломка – вспомним «извращения» этюда 3) длился бы нестерпимо долго. Несложный предварительный анализ условий задачи (U ¬ 9, Р ¬ 1, Е ¬ 0 и R ¬ 10 + A) сокращает число циклов до трех и делает время счета приемлемым. Один из основных недостатков языка Mathcad – это невозможность вывода на дисплей промежуточных результатов расчета. А они не только помогают отлаживать программы, но и в ряде случаев просто необходимы при поиске единственно правильного решения из множества возможных (см., например, программы на рис. 6. 34 и 35 с решением задачи о компьютерах). В Mathcad-программах допустима запись вариантов ответов (промежуточных результатов) в матрицу (в вектор), которую после выполнения программы можно просмотреть, что и сделано на рис. 6.6. При этом в матрицу M записываются не только значения числовых переменных, но и текстовые константы[13]
(“+”, “=” и др.), делающие ответ более читабельным. Правильный ответ хранится в первом столбце матрицы M. Вернее, в первой строке – матрица у нас транспонируется для большей компактности[14]. Остальные ответы неверны – там разным буквам соответствуют одинаковые числа.
Цикл с параметром в среде Mathcad более гибок, чем его аналоги в языках BASIC или Pascal. Вот еще варианты заголовков циклов с параметром в среде Mathcad, кроме тех, которые показаны на рис. 6.6 (там специально приведены разные варианты заголовков циклов):
for A Î V (V – вектор)
for A Î 5, 4.7, 8.9, 7.3×10-5
for i Î i1.. i2.
Последний вариант примечателен тем, что переменные i1 и i2 могут принимать любые значения, и необязательно, чтобы i1 было меньше i2. В языках BASIC и Pascal разное соотношение между i1 и i2 требует различного синтаксиса заголовка цикла с параметром:
For i= i1 To i2 или For i=i2 To i1 Step -1 (BASIC)
for i:=i1 to i2 do или for i:=i2 downto i1do (Pascal).
Кнопки



Все структурные управляющие конструкции Mathcad можно усмотреть в простой житейской ситуации: потчевание гостей чаем и кофе. Хозяйка проверяет, нет ли на столе пустой чашки (булева переменная, управляющая циклом while), и наполняет ее (тело цикла) чаем или кофе (альтернатива). Добавление в чашку кусочков сахара – новый, вложенный цикл. При разливе чая чашка (стакан) может лопнуть, что прерывает цикл, из которого выходят в конец цикла (break – гости встают из-за стола и занимаются чем-то другим) или в начало цикла (continue – на столе меняется скатерть и чаепитие возобновляется). Третий сценарий: разбитая чашка так расстраивает хозяйку, что вечеринка досрочно заканчивается (return).
Ниже приведены другие примеры программ в среде Mathcad.
Общие замечания. Язык программирования Mathcad по своей идеологии очень похож на язык FRED интегрированного пакета Framework. Говорят, что один из «погорельцев» фирмы Ashton-Tate (разработчика Framework) перешел в фирму MathSoft и приложил руку к созданию языка программирования Mathcad. Внешне же своими вертикальными линиями, фиксирующими вложения конструкций программы и операторные блоки, пакет Mathcad напоминает алгоритмические конструкции книги А.П.Брудно «Программирование в содержательных обозначениях» (М.: Наука, 1968). В свое время я очень увлекался подобными линиями, втискивая программы в рамки структурных диаграмм (см. рис. 6.21, а также книгу «128 советов начинающему программисту». – М.: Энергоатомиздат, 1991). Вертикальные линии программ Mathcad более наглядны (особенно для обучения структурному программированию), чем просто операторные скобки (begin-end на языке Pascal, фигурные скобки языка С, оператор list() языка FRED, конец строки BASIC-программы, круглые скобки математических выражений и т.д.).
Говоря о структурном программировании, нельзя не отметить тот факт, что разработчики языка Mathcad отказались от метки и операторов условного и безусловного перехода к метке как инструмента реализации разветвленных алгоритмов. Для некоторого смягчения этой категоричной позиции и были введены операторы return, break и continue.
Программа-константа
Программу, формирующую константу, подобрать несложно. Но зачем? Константу можно раз и навсегда рассчитать (задать), а потом вставлять результат в Mathcad-документ (константы p, е и др.). Но иногда для лучшего понимания сути константы полезно оставить механизм ее формирования открытым. Программа на рис. 6.7 подсчитывает число, фигурирующее в легенде об изобретателе шахмат, который в награду попросил дать ему такое количество зерна, какое он может положить на шахматную доску с тем, чтобы на первой клетке было одно зернышко (21-1 т.е. 20), на второй – два (22-1), на третьей – четыре (23-1) и т.д. (на новой клетке зерен в два раза больше, чем на предыдущей). На рис. 6.7 подсчитывается не все количество зерен на шахматной доске, а их масса в британских тоннах, не превышающая 100 000 тонн (масса одного зерна принята за 0.3 грамма).
Программы-переменные и программы-функции читатель увидит ниже.
Программа-скаляр
Программа на рис. 6.8 возвращает скалярное значение – номер элементов (iopt) векторов X, Y и Z при котором... В этюде 3 мы искали домик на дачном участке, где следует устроить, например, продовольственный ларек. Критерий выбора – минимальная сумма расстояний от ларька до всех остальных домиков. Теперь (рис. 6.8) ларек у нас уже космический, а задача трехмерная. На рис. рис. 3.12 подобная задача решалась без привлечения инструментов программирования.
Программы на рис. 3.12 и 6.8 довольно примитивны. Но читатель может их развить, заменив, например, декартову систему координат на географическую, где вектор X будет хранить значения долготы, а вектор Y – широты
объектов. Тогда задача может свестись к поиску места, например, для вертолетной площадки, обслуживающей геологов или нефтяные скважины, и стать не только более сложной, но и более реальной[15].
Программа-матрица (пасьянс «Турецкий платок»)
Рассмотрим эту особенность на такой занимательной задаче.
Очень часто, решая ту или иную проблему, мы оказываемся в шкуре буриданова осла. Задача может иметь два альтернативных решения, как две охапки сена слева и справа от упомянутого животного. Все доводы «за» и «против» уравновешены. Как в этом случае поступить? Ехать или не ехать в командировку? Покупать или не покупать еще один винчестер? Поистине, гамлетовские вопросы задает нам жизнь!
Некоторые в таких ситуациях бросают монетку, другие загадывают мужчину или женщину и смотрят в окно, ожидая, кто первый появится. Но все это ненаучные методы. Монетка может куда-нибудь закатиться, а по улице как назло за целый час только кошка и пробежит...
Есть проверенный столетиями метод принятия подобных решений. Достаточно разложить пасьянс. Сошелся – решение принято и все сомнения прочь. Можно подыскать дополнительные доводы в его пользу, и начать воплощать в жизнь. Пасьянс психологически нас на это настраивает.
Но принять решение подобным образом иногда бывает трудно, так как не всегда под рукой есть колода карт, да и не совсем удобно раскладывать их на рабочем месте. Но это можно сделать и на экране дисплея. В среде Windows, например, есть игры-пасьянсы («Солитер» и «Косынка»), но мы придумаем что-нибудь новенькое, а, главное, более занимательное и поучительное – разложим в среде Mathcad старинный пасьянс «Турецкий платок». На это есть три причины:
1.Чтобы лучше освоить программную среду, нужно постараться решить в ней задачу, для этого крайне неподходящую. Да, это своего рода программистское извращение, но – см. этюд 3.
2.В детстве каждый нормальный человек, наигравшись, ломал игрушку, чтобы посмотреть, как она устроена. Посмотрим и мы, как тасуется колода и раскладывается пасьянс.
3.По традиции гадать на картах и раскладывать пасьянсы разрешается только в святки[16]. Наш пасьянс можно считать числовой головоломкой, которую позволительно решать круглый год.
Mathcad-документ (см. рис. 6.9) позволяет разложить пасьянс «Турецкий платок» по следующим правилам. Из одной перетасованной колоды в 52 листа выкладывают картинкой вверх пять рядов по 10 карт в каждом. Последние две карты кладут в шестой неполный ряд на любое место, как правило, к первому и второму столбцам. Требуется распустить этот «платок», снимая из разных столбцов за один ход по две нижние одинаковые карты – тройки, дамы, тузы и т.д.
Для снятия карт нужно скопировать правую часть оператора П = ... (саму матрицу) на свободное место, подвести курсор к нужной текстовой константе (к карте), щелкнуть по левой кнопке мыши и нажать клавишу Delete. Вместо числа появится пустой квадратик.
Из разложенного пасьянса сняты две двойки. Теперь можно снять две восьмерки, два короля или две десятки (вопрос – какие из трех открытых). После этого откроются новые карты. Если удастся снять все 52 карты, то это означает, что в командировку все-таки ехать придется, а винчестер покупать надо.
Составление программы, формирующей матрицу П (раскладка пасьянса) – прекрасное и, что не менее важно, занимательное средство изучения таких базовых понятий линейной алгебры, как вектор и матрица. Так, при формировании матрицы П транспонируется матрица Масть (она ставится «на попа» – матрица с одной строкой превращается в матрицу с одним столбцом, то есть в вектор). Далее с помощью функции stack составляется новая нерастасованная колода карт, где одна отсортированная масть идет за другой (вектор Колода). Затем в цикле с параметром (for...) с помощью цикла while[17] и функции rnd идет формирование перетасованной колоды – вектора Тасованная_колода, который в конце программы двойным циклом с двумя параметрами (for... for...) складывается слоями в матрицу П.
Программу, формирующую матрицу П, можно развить: заставить программу отбраковывать явно нерешаемые раскладки – такие, например, где в одном столбце оказались три или даже четыре одинаковые карты. Еще одна тупиковая ситуация – две пары карт крест накрест закрывают друг друга. Это будет хорошим упражнением, закрепляющим навыки работы с «матричными» операторами и функциями в среде Mathcad. А вот более сложное задание читателю: доработать программу так, чтобы она сама раскладывала пасьянс, либо на худой конец сообщала, что его можно решить, просто снимая снизу первые подвернувшиеся одинаковые открытые карты. Более умная стратегия подразумевает выбор карты из трех или четырех одинаковых открытых карт.
Кроме линейной алгебры, наша программа затрагивает и другие интересные разделы математики – теорию вероятностей, статистику (см. функцию rnd, генерирующую псевдослучайные числа). Интересный вопрос: можно ли составить программу, высчитывающую вероятность сходимости того или иного пасьянса? Считается, что пасьянс «Солитер», входящий в стандартную поставку Windows, раскладывается при любых начальных раскладках. Но это только гипотеза…
Часто бывает так, что человек прекрасно делает то, чему он учился играючи и с большим удовольствием: ходит, говорит, плавает, катается на велосипеде и т.д. и т.п. Автор, например, задолго до школы научился считать, играя в карты: валет – двойка, дама – тройка и т.д. И сейчас, обращаясь к своим студентам, не устает повторять, что главное, что нужно получать от учебы, – это не знания, не практические навыки, а... удовольствие. Не получая радости от учебы, от повседневного труда, человек тратит свою жизнь впустую... Например, если тяжело идет освоение линейной алгебры – расслабьтесь и постарайтесь получить удовольствие.
Начинать изучение векторов и матриц (массивов данных) в курсе программирования (информатики) можно со знакомства со встроенными функциями и операторами конкретной программной среды. А можно раскладывать пасьянсы.
Как уже отмечалось ранее, переменные в Mathcad могут быть локальными, самообъявляющимися в программах (как, например, переменные Случайное_число, Колода, Карта, Столбец и Ряд в программе на рис. 6.9). Значение локальных переменных пропадает по выходу из программы. Разработчики языка Mathcad посчитали лишним обязательное объявление переменных до их использования (как это делается при работе с языком Pascal, например). Наверное, переменные не объявляются из-за того, что они все однотипные[18]. Но необъявление переменных может приводить к ошибкам, которые трудно выявить, так как язык Mathcad не имеет средств отладки
(debugging). Ввел программист в программу переменную dаy, а через пару операторов написал dey (что по произношению более соответствует английскому слову day (день); можно умудриться написать и dаy, где вторая буква будет из русского алфавита) – программа выдает неверный ответ. Опечатки в программе часто бывают намного страшней в плане отладки, чем ошибки алгоритма. Кроме локальных и глобальных переменных, значения которых заданы вне программы и автоматически в нее проникают, в среде Mathcad есть и системные (предопределенные) переменные и константы. Пример – числа e и p, значение которых определено самой системой (математикой), а не пользователем (см. приложение 4).
Мы уже не первый раз используем буквы кириллицы в именах переменных и функций. В программе на рис. 6.9 впервые все переменные прописаны по-русски. Pro и Contra этого приема.
Pro[19]:
Полные имена переменных (Столбец, Ряд вместо i, j) делают программу более простой для понимания, но более сложной для написания (рекомендуется длинные переменные писать один раз, а потом копировать в нужных местах). Конечно, можно было написать и английские термины в качестве имен переменных, но они будут выглядеть чужеродными в пасьянсе, программу которого для русскоязычного читателя написал человек, считающий себя русским. Да и автор, честно говоря, не знает, как будет по-английски «Масть», «Колода». Лезть же в словарь не с руки. Проще написать Мast, Коloda. Проще, да некрасиво (см. ниже).
Contra:
Русские имена переменных порождают «смешенье языков французского с нижегородским»: for Столбец?! Правильнее и грамотней писать for Солбца[20] (для Столбца); на многих программистов русское имя объекта программирования (файла, переменной, функции и т.д.) действует как красная тряпка на быка[21].
В латинском и русском алфавитах многие буквы (например, а, с) совпадают по написанию. Из-за этого в программе могут оказаться переменные, одинаковые для человека, но разные для Mathcad.
Выбор для переменных шрифта с окончанием Cyr приводит к перекодировке символов. Из-за этого, например, может пропасть восклицательный знак в факториале и др.
Расчет факториала (двусторонняя рекурсия)
Работая по программе с двусторонней рекурсией, показанной на рис. 6.10, можно не только правильно определить факториал нуля (единица), но и получить факториалы отрицательных (?!) чисел. Только нужно обучить этому машину – заложить в программу двустороннюю рекурсию для поиска факториала на всем целочисленном диапазоне[24]. «Двусторонность» здесь проявляется в том, что факториалы ищутся не только справа, но и слева от пяти.
Описывая в этюде 5 модель финансовой пирамиды, мы упомянули числа Фибоначчи, которые связаны с условными кроликами:
| Поколение | ... | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... | |||||||||||
| Число кроликов | ... | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | ... |
Приведенный ряд специально начат не с традиционного места (первое поколение), а с четвертого поколения (три кролика), для того чтобы задать читателю вопрос, подобный тому, который стоял в задаче о факториале: «Чему равно минимальное число кроликов в популяции – каково наименьшее число Фибоначчи?» Нормальный ответ, приводимый во всех учебниках, – ноль. Но не будем спешить и напишем программу с двусторонней рекурсией, взяв за базовые числа Фибоначчи не традиционную пару 0 и 1, а 13 и 21 (седьмое и восьмое поколения – см. рис. 6.11).
Расчет чисел Фибоначчи (двусторонняя рекурсия)
Ряд кроликов Фибоначчи в «отрицательных поколениях» зеркально отображает значения в «положительных поколениях», но с переменным знаком.
Числа Фибоначчи в наше время широко применяются в вычислительной математике, в том числе и для иллюстрации рекурсии, как, например, в нашей книге. Кроме того, метод Фибоначчи используется для поиска минимума. Частный случай метода Фибоначчи – метод золотого сечения (см. рис 6.26): пара смежных чисел Фибоначчи при N, стремящемся к бесконечности, соотносится по золотому сечению.
Расчет изящных чисел Фибоначчи (двусторонняя рекуррентность)
Использование рекурсии для поиска чисел Фибоначчи – это стрельба из пушки по воробьям. Намного эффективнее рассчитывать подобные числа в цикле, рекуррентно. На рис. 6.12 представлена программа, по которой ищутся, если так можно выразиться, изящные (fine) числа Фибоначчи[25], где базой будут тройка, семерка[26] и туз (11). Следующим изящным числом Фибоначчи будет 21 (3+7+11, тоже красиво – вспомним знаменитую карточную игру). Предыдущим числом окажется 1 (11-7-3, опять неплохо, если принять во внимание, что сестра таланта не только краткость, но и простота). Остальные изящные числа Фибоначчи, пользуясь программой на рис. 6.12, рассчитать несложно – главное тут суметь дать им «изящное» толкование.
В программе на рис. 6.12 еще раз подчеркнуто, что размещение нескольких операторов на одной строке – это недокументированный прием. Если такая «упакованная» программа будет давать неверный результат, то фирма MathSoft за это ответственности не несет. Мы же будем считать такую программу «заархивированной» и не занимающей много места в книге. Такую программу при вводе в компьютер требуется «разархивировать».
Другой резон размещения нескольких операторов на одной строке лежит в сфере образования. Автор просит своих студентов операторы, не находящиеся в причинно-следственной связи, писать на одной строке – A
< 1 B
< 2, например. Оператор же, который опирается на предыдущий (предыдущие), следует писать внизу:
| A < 1 B < 2 C < A + B |
Так можно имитировать параллельные вычисления на однопроцессорной машине: считается, что операторы на одной строке выполняются одновременно, а записанные столбиком – последовательно.
Задание читателям на закрепление пройденного: сделать программу на рис. 6.11 рекуррентной, а на рис. 6.12 – рекурсивной[27].
Расчет чисел Аккермана
Есть более крепкий орешек – числа Аккермана, зависящие уже от двух переменных (см. рис. 6.13 с двойной рекурсией). В среде Mathcad числа Аккермана можно рассчитать только для значений аргументов m и n, находящихся недалеко от нулей («каботажное плавание»). Расчет, например, значения Akk(4, 6) через некоторое время аварийно прерывается – см. рис. 6.13. Рекурсия – это когда программист, сокращая текст программы, перекладывает свои проблемы на плечи машины, которой приходится генерировать длинный ряд новых локальных переменных. Отсюда и сбои. Выход из положения – замена рекурсии на рекуррентность (цикл), что автор и предлагает сделать читателям по отношению к числам Аккермана.
Для закрепления темы рекурсии приводим текст BASIC-программы, решающей известную головоломку «Ханойские башни»[28]
(рис. 6.14):
DefInt N
DefStr X-Z
Declare Sub PUTDISK (N%, X$, Y$, Z$)
Input "Число дисков в пирамиде"; N0
PUTDISK N0, "A", "B", "C"
End
Sub PUTDISK (N%, X$, Y$, Z$)
DefInt N
DefStr X-Z
If N = 1 Then
Print X; "-"; Z
Else
PUTDISK N - 1, X, Z, Y
Print X; "-"; Z
PUTDISK N - 1, Y, X, Z
End If
End Sub
BASIC-программа «Ханойские башни»
Суть головоломки. Имеется три стержня, на первый из которых (у нас в программе на рис. 6.14 он маркирован как A) нанизаны диски на манер детской пирамидки: самый большой диск внизу – самый маленький наверху. Предлагается переложить эти диски на второй стержень (C), беря их по одному и не кладя большой диск на маленький. Для временного складирования разрешается использовать третий диск (B). Программе на рис. 6.14 достаточно сообщить только число дисков в пирамиде N. После запуска программа будет возвращать порядок перекладки дисков:
N=2: A-B, A-C и B-C (три хода)
N=3: A-C, A-B, C-B, A-С, В-A, B-C и, наконец, A-C (семь ходов)
N=4: …(15 ходов) и т.д.
Число перестановок в общем случае равно 2N-1. Задача с N дисками легко сводится к задаче с N-1 дисками, а задача с N-1 дисками легко сводится к задаче с N-2 дисками и т.д. до задачи с двумя дисками, которая решается просто – A-C (см. на рис. 6.14 фрагмент программы If N = 1 Then Print X; "-"; Z). Отсюда и рекурсия в программе на рис 6.14.
Задание читателям[29]
– переписать BASIC-программу на рис. 6.14 для Mathcad. Подводный камень: BASIC-программа оператором Print выдает результат из подпрограммы. В языке Mathcad это сделать невозможно – там допустимо сначала полностью заполнить матрицу, и только потом вывести ее на дисплей.
По легенде тибетские монахи уже несколько тысячелетий перекладывают 64 золотых диска, нанизывая их на алмазные стержни. Когда головоломка будет решена и на стержне C окажутся все диски, наступит конец света. Спасает нас лишь то, что при 64 дисках для решения головоломки потребуется:

Это без учета ложных ходов и времени, необходимого на ручной или компьютерный расчет порядка перестановки дисков.
Размерность в программе
Тип числовой переменной в среде Mathcad, как уже было отмечено в этюде 1, в какой-то мере заменяется размерностью хранимой величины, что очень удобно в инженерных расчетах. По программе на рис. 6.15 рассчитывается площадь треугольника (пункт 1). Аргументами функции Площ_треуг могут быть величины с разной размерностью длины (метры – m, сантиметры – cm, дюймы – in). Система Mathcad сама в них разберется, сделает нужные пересчеты и выдаст правильный результат в выбранной пользователем системе единиц (кг-м-с, г-см-с, СИ или британская).
Система Mathcad, кроме того, ведет контроль размерностей и не позволяет складывать, например, метры с килограммами или секундами (см. соответствующее встроенное сообщение об ошибке в конце пункта 1 на рис. 6.15).
Функция в среде Mathcad, как уже отмечалось, может возвращать несколько значений, объединенных в вектор. Программно заданная пользовательская функция в пункте 2 на рис. 6.15 возвращает значение периметра и площади треугольника. Но если пользователь захочет сделать размерными аргументы, чтобы функция вернула ему значение периметра и площади треугольника с соответствующими размерностями (пункт 3), то его ждет неудача. При этом будет выдано дезинформирующее сообщение об ошибке: «Несоответствие единиц измерения». Пользователь будет думать, что он складывает метры с килограммами, как в пункте 1. Но причина в другом – вектор в среде Mathcad может хранить переменные только одной размерности. Из-за этого нам уже пришлось отказаться от размерностей при решении задачи о равновесии балки – сравните рис. 1.15 и 1.16.
Можно заставить функцию выдавать две величины не сразу, а попеременно – в зависимости от значения дополнительного аргумента (пункт 4): если i = “Периметр”, то функция Параметры_треуг возвращает периметр треугольника, если i = “Площадь”, то – площадь. Но и здесь работа с размерностями будет приводить к сбоям – см. пункт 5 на рис. 6.15. Функция Параметры_треуг всегда возвращает размерность переменной из последней строки программы.
Ошибок в среде Mathcad, как и в любой другой программной среде, достаточно. Автор акцентирует внимание на этой ошибке по двум причинам. Во-первых, автор когда-то убил уйму времени, отлаживая программу, подобную программе на рис. 6.15, и не понимая, в чем суть ошибки. Во-вторых, дал об этом знать разработчикам Mathcad, но в восьмой версии эта ошибка почему-то не была исправлена. Кстати, об ошибках…
Считается, что по-настоящему красивая женщина («чертовски красивая») непременно должна иметь внешний дефект (ошибку Природы), небольшой, но сразу бросающийся в глаза: вздернутый нос, родинка, веснушки... Такие «украшения» лишний раз напоминают о том, что это не богиня, от которой лучше держаться подальше, не бездушная «кукла восковая», а земная женщина. Вот хрестоматийный пример: Наталья Николаевна Пушкина (урожденная Гончарова) – петербургская красавица, которая тем не менее чуть-чуть косила[30]. А вот другой пример – Шекспир воспел «смуглую леди сонетов» в те времена, когда белизна лица считалась непременным атрибутом женской красоты.
Слово «чуть-чуть», только что промелькнувшее в тексте, напоминает о кратком, но точном определении художественного вкуса: «Искусство – это чувство меры». Рафинированное произведение искусства, созданное на основе чистых канонов, находится как бы в неравновесном состоянии. Маленький щелчок («глюк» в программе, родинка на лице красавицы или ее легкое косоглазие, кривая колокольня в Пизе, корявый автограф в углу картины или темный штрих в биографии художника или программиста[31], на худой конец) сталкивает эту шаткую балансирующую конструкцию либо в чулан поделок (кич), либо в сокровищницу шедевров.
А вот еще пример, поворачивающий проблему на новую грань, где пересекаются плоскости формы и содержания. Сергей Довлатов в своих записках упоминает об известном профессоре-филологе с такими косыми глазами, что с ним трудно было общаться – непонятно, в какой глаз нужно смотреть. Этот профессор, прикрывая рукой левый глаз, говорил собеседнику: «Смотрите в правый. На левый не обращайте внимания. Левый – это дань формализму». Хорошо дурачиться, создав предварительно целую филологическую школу – ошибки простительны только в гениальных программах.
Если читатель увидит опечатки или даже ошибки в этой книге, то автор просит, во-первых, сообщить об этом автору, а, во-вторых, перечитать то, что написано выше.
Работа с размерностями вообще требует особой аккуратности. Вот хороший совет при работе в среде Mathcad. Вводить в Mathcad-документ новую переменную лучше оператором «m=» (вывод значения), а не оператором «m:=» (ввод значения). Этим пользователь проверяет лишний раз, не занята ли уже переменная m хранением заданной ранее величины. В Mathcad 7 и 8 этот прием не обременителен, так как в среде этих версий оператор «m=» автоматически (Smart Operator) превращается в оператор «m:=», если переменная m свободна от хранения чего-либо.
Предпроверку переменных особо можно рекомендовать в расчетах с использованием размерностей физических величин[32]. В этом режиме (а он включается по умолчанию) предопределенными (системными) будет огромное число «популярных» переменных (A, c, C, F, g, H, J, K, L, m, N и т.д. – см. приложение 7), хранящих единичные значения физических величин (сила тока, скорость, заряд, емкость, ускорение, индуктивность, энергия, температура, длина, количество вещества и т.д.). В таком расчете «невинное» выражение «m:=3» развалит весь стройный порядок единиц измерения: вместо метров появится черт знает что.
Метод Ньютона I (BASIC): цикл с выходом из середины
На рис. 6.16
приведена BASIC-программа поиска корня алгебраического уравнения методом Ньютона (касательных). Почему мы начали с языка BASIC, ведь этюд посвящен языку программирования Mathcad? Дело в том, что язык BASIC кроме традиционной тройки циклов (цикл с предпроверкой, цикл с постпроверкой, цикл с параметром) имеет и универсальный цикл с выходом из середины: Do [...] If ... Then [...] Exit Do [...] Loop. Эта конструкция наряду с другими преимуществами, о которых будет сказано ниже, позволяет реализовывать алгоритмы в их естественной последовательности. Так, в программе на рис. 6.16 объявляются функции пользователя (анализируемое уравнение y и его производная dy), запрашивается значение начального приближения к корню x и задается значение погрешности TOL. После этого организуется цикл, но не традиционный, а с выходом из середины. В цикле, следуя естественному порядку алгоритма Ньютона, рассчитывается новое приближение к корню (x1), и если оно отстает от предыдущего не более чем на величину заданной погрешности[34], то (Then) задача считается решенной (Exit Do). Если нет, то ведется подготовка к новому приближению (x = x1), а цикл повторяется (Loop).
При реализации на языке Mathcad этот несложный алгоритм обрастает «архитектурными излишествами», так как его приходится реализовывать функцией и «запихивать» в прокрустово ложе цикла while – см. рис. 6.17.
Метод Ньютона II: цикл с предпроверкой
Цикл с предпроверкой (цикл while) требует, чтобы булево выражение заголовка было определено еще до входа в цикл. А этого нет при поиске корня методом Ньютона. Приходится до входа (и для входа) в цикл писать x1 ¬ x + 2 × TOL. Подобным образом лгут детям (а машина тоже в каком-то смысле дитя), заставляя их что-то делать. Строку x1 ¬ x + 2 × TOL можно уподобить стартеру двигателя внутреннего сгорания, работающего, кстати, как и программа на рис. 6.17, циклически. Вот какими аллегориями (дитя, двигатель) обросла наша простенькая программа из-за того, что в языке Mathcad нет цикла с выходом из середины. На рис. 6.17 можно отметить и другую ненатуральность программы – постановку телеги впереди лошади: в цикле сначала приходится готовиться к новому приближению (x1 ¬ x), хотя еще не ясно, понадобится оно или нет, а только потом проводить его.
Операторы break, continue и return, введенные в Mathcad, призваны вернуть программе на рис. 6.17 ее естественность, но...
Метод Ньютона III: имитация цикла с выходом из середины
BASIC-конструкция Do ... Loop (см. рис. 6.16) на рис. 6.18 превратилась в конструкцию while 1 ..., которую на латинский язык можно перевести как «ad calendas greaces» – «до греческих календ». Здесь, как и в программе на рис. 6.17, пришлось идти если не на обман, то на натяжку: «выполняй, пока рак на горе не свистнет».
Оператор continue отличается от оператора break тем, что передает управление не в хвост, а в гриву (начало) цикла[35]. Но в документации и в файлах помощи Mathcad нет примеров, обосновывающих использование оператора continue. Не смог придумать их и автор.
История с вводом в Mathcad операторов break и continue и return подтверждает старую истину о том, что «нет ничего практичнее хорошей теории». И вот почему.
Вышеприведенный анализ циклов на языке Mathcad имеет не только сугубо практический, но и чисто теоретический аспект. Как известно, набор управляющих конструкций любого структурного языка ведет свою родословную от основной структурной теоремы Дейкстры, объявившей войну меткам: «Алгоритм любой сложности можно реализовать, используя только цикл while и альтернативу». Автор потратил уйму времени и сил на поиск доказательства этой теоремы в статьях или книгах, но так ничего и не нашел. А вот показать, что данная теорема не верна, можно в два счета – см. рис. 6.19 и рис. 6.20. Эти программы решают уже известную нам задачу о корне алгебраического уравнения, но другим методом – методом половинного деления. Его алгоритм – простейшая иллюстрация теоремы Дейкстры: цикл (while) приближения к корню, в которой вложена альтернатива (if ... ). Если корень правее центра интервала a-b, то к нему (к центру) подтягивается левый край (a ¬ x), если нет – правый (b ¬ х).
Метод половинного деления I (Mathcad)
В программе на рис. 6.20 альтернатива программы на рис. 6.19
заменена на два цикла while, операторы тела которых попеременно выполняются либо раз, либо ни разу, что регулируется булевой переменной Flag.
Метод половинного деления II (Mathcad)
Кроме того, в программе на рис. 6.20 проведена чистка цикла, в теле которого значение анализируемой функции рассчитывается всего раз. В программе на рис. 6.19 это делалось два раза. Второе изменение в программе на рис. 6.21
по сравнению с программой на рис. 6.19
состоит в том, что не используется функция Хевисайда. Букву Ф у нас принимают не за греческую букву «фи», а за русскую букву «эф» и делают ошибку, которую трудно понять и поэтому тяжело исправить. Функцию Хевисайда заменяет произведение значений анализируемой функции на концах вилки. Булева операция And в программе на рис. 6.20 вызывается не в виде функции And(..., ...), а древовидным оператором.
Метод половинного деления III (QBasic)
В аналогичной BASIC-программе (на рис. 6.21 она вписана в структурную диаграмму) также обошлись без альтернативы. Более того, удалось избавиться и от переменной-диспетчера Flag, заменив два цикла while на один цикл, но с двумя выходами из середины – одним условным, а вторым безусловным.
Весь фокус программ на рис. 6.20 и 6.21
в том, что альтернатива – это средство ускоренного «путешествия» по алгоритму только в одну сторону (сверху вниз и слева направо), а цикл – в обе. Отсюда и ненужность (в теоретическом плане, конечно, а не в практическом[36]) альтернативы. Цикл Do [...] If
... Then [...] Exit Do [...] Loop можно считать гибридом цикла и альтернативы.
Доказательством теоремы Дейкстры может служить факт, что до сих пор не было случая, когда задуманный алгоритм нельзя было бы реализовать, используя только цикл и альтернативу[37]. Если альтернативу исключить, то основная структурная теорема должна звучать так: «Алгоритм любой сложности можно реализовать, используя только цикл». Вот это-то теоретическое положение вводом операторов break, continue и return подсовывает задним числом язык программирования Mathcad под свой фундамент. Обращаю внимание на несовершенный вид глагола – «подсовывает», а не «подсунул» – цикл с выходом из середины на языке Mathcad осуществим через насилие над циклом while (рис. 6.18). При этом приходится писать в заголовке цикла какую-нибудь тривиальную истину: «Волга впадает в Каспийское море».
Теорему Дейкстры следует «понизить в звании» и называть леммой, то есть вспомогательной теоремой, служащей для доказательства основной.
Здесь мы вернулись к спорам, бушевавшим лет 30 назад. Операторы break, continue и return, введенные в язык Mathcad, дали нам повод напомнить о них. Эти операторы по принципу «и вашим и нашим» примирили сторонников и противников оператора перехода к метке.
Задача о рыбаках и рыбке: «беспрограммное» решение в среде Mathcad
На рис. 6.22 показано, как задача решается методом последовательных приближений – задается первое приближение к ответу (50 рыб), а затем от этого числа отнимается по единице до тех пор, пока убывающий улов не будет представлять собой целочисленный ряд: было 25 рыб (искомый ответ задачи), первый рыбак выбросил одну, забрал треть и оставил товарищам 16 рыб (по 8 каждому); второй рыбак (не зная, что первый ушел) оставил 10 рыб, а третий – 6. Задача решена, но с применением «ручной» работы, состоящей в наблюдении за значениями переменной Улов и в изменении (уменьшении на единицу) значения переменной Ответ. (Блоки операторов, фиксирующих действие трех рыбаков, можно не дублировать, как это сделано на рис. 6.22. Достаточно уменьшать[38]
значение переменной Ответ и следить за значениями переменной Улов).
Попробуем автоматизировать поиск ответа в задаче о рыбаках и рыбке.
‘ 1. Исходная неструктурированная Basic-программа
Input "Предположение"; Ответ
label: Улов = Ответ
For Рыбак = 1 To 3
Улов = Улов – 1
Улов = Улов - Улов / 3
If Улов > Int(Улов) Then Ответ = Ответ - 1: Goto label
Next
Print "Ответ "; Ответ; “рыб”
‘ 2. Первый шаг структурирования - разбег
Input "Предположение"; Ответ
Ответ = Ответ + 1 ‘ Шаг назад
label: Ответ = Ответ - 1 ‘ Шаг вперед
Улов = Ответ
For
Рыбак = 1 To
3
Улов = Улов – 1
Улов = Улов - Улов / 3
If Улов > Int(Улов) Goto label
Next
Print "Ответ "; Ответ; “рыб”
‘ 3. Второй шаг структурирования – ввод признака
Input "Предположение"; Ответ
Ответ = Ответ + 1
label: Ответ = Ответ – 1
Улов = Ответ
Поделили = "да" ’ Признак дележа улова
For Рыбак = 1 To 3
Улов = Улов – 1
Улов = Улов - Улов / 3
If Улов > Int(Улов) Then
Поделили = “нет”
Next
If Поделили = “нет Goto
label
Print "Ответ "; Ответ; “рыб”
‘ 4. Третий шаг структурирования – отказ от метки
Input "Предположение"; Ответ
Ответ = Ответ + 1
Do ’ Начало цикла с постпроверкой
Ответ = Ответ – 1
Улов = Ответ
Поделили = "да"
For
Рыбак = 1 To
3
Улов = Улов – 1
Улов = Улов - Улов / 3
If
Улов > Int(Улов) Then
Поделили = “нет”
Next
Loop Until Поделили = "да" ’ Конец цикла
"Ответ "; Ответ; “рыб”
BASIC-программы решения задачи о рыбаках и рыбке
На рис. 6.23 представлены четыре Basic-программы, решающие задачу о рыбаках и рыбке в автоматическом режиме: оператор Input запрашивает первое приближение (те же 50 рыб, к примеру), а оператор Print выдает ответ – 25 рыб. В первой BASIC-программе один к одному реализован алгоритм «ручного» расчета: как только в теле цикла с параметром (три последовательных ухода рыбаков) переменная Улов обретает дробный «хвостик» (встроенная BASIC-функция Int этот «хвостик» обрезает; ее Mathcad-аналог – функция floor), то (Then) предположение уменьшается на единицу (Ответ = Ответ - 1), а управление программой передается к оператору, помеченному меткой (Goto label). Прежде чем эту программу перевести на язык Mathcad, ее нужно освободить от метки[39]. И не только потому, что в арсенале средств программирования Mathcad нет метки и операторов условного и безусловного перехода к метке, но по другим причинам, не связанным с Mathcad. В нашей коротенькой программе-безделушке (пункт 1 на рис. 6.23) метка вполне уместна и естественна, но если программа с метками разрастается, то в ней становится трудно разбираться и ее практически невозможно отлаживать и расширять. Программа, как справедливо подчеркивают адепты структурного программирования, становится похожа на спагетти: вытаскиваешь (вилкой) блок операторов для отдельной отладки или компиляции, а к нему намертво привязаны нити (макаронины) Goto-переходов. Кроме того, такую программу невозможно создавать группой разработчиков (технология снизу вверх). Первые реализации языка Pascal совсем не имели меток, так как этот язык разрабатывался Н.Виртом в первую очередь для обучения студентов структурному программированию. Метка появилась только в поздних версиях этого языка. Так от детей в период, когда они учатся жить (выживать!), прячут спички.
Первый шаг структурирования BASIC-программы на рис. 6.23 – это превращение конструкции:
If
Улов > Int(Улов) Then
Ответ = Ответ - 1: Goto label
в оператор условного перехода к метке:
If Улов > Int(Улов) Goto label
Это сделать несложно (см. пункт 2 на рис. 6.23), применив в программе технику разбега спортсмена перед прыжком: шаг назад от черты-метки (Ответ = Ответ + 1) и разбег (Ответ= Ответ - 1). Структурирование программы, как правило, несколько усложняет алгоритм: «За все нужно платить!», «Красота требует жертв!» и т. д.
Второй шаг структурирования – это вытаскивание оператора безусловного перехода из тела цикла For. Для этого в программу (см. пункт 3) вводится вспомогательная булева переменная-признак Поделили, а в теле цикла оператор условного перехода к метке заменяется на оператор «альтернатива с одним плечом» (одна из основных структурных управляющих конструкций). Сам же оператор условного перехода «сползает» вниз. После этого в программе «вырисовывается» еще одна основная структурная управляющая конструкция – цикл с постпроверкой, который в третьем варианте на рис. 6.23 реализован через метку и оператор условного перехода к метке. После этого программу наконец-то можно совсем освободить метки, реализуя алгоритм через цикл с постпроверкой, в тело которого вписан цикл for, а в него ¾ альтернатива с одним плечом (пункт 4).
После всех этих манипуляций четвертый вариант BASIC-программы можно один к одному переписать для Mathcad – см. рис. 6.24. Придется только оформить ее в виде функции пользователя: в языке Mathcad нет операторов Input и Print[40]. Их аналоги в среде Mathcad (операторы - := - и - =) работают, увы, только вне программ.
Mathcad-программа решения задачи о рыбаках и рыбке
На рис. 6.24 показаны вызовы функции Ответ при различных значениях предположений (50, 24, минус 3 и даже минус 30 рыб). Английский физик Поль Дирак придумал не только античастицы, но и «антирыбы»: он сказал, что задача о рыбаках и рыбке решалась неправильно (25 рыб). Правильный ответ – минус две рыбы (плюс две антирыбы): выбрасываем одну – остается минус три, забираем треть – остается минус две и так до бесконечности. Наше компьютерное решение задачи показывает, что и Дирак ошибался: «Поль, ты не прав!» Условию задачи отвечает бесконечный ряд чисел (назовем его «рыбный ряд Дирака») с шагом 27.
Чтобы не прослыть совсем уж полным педантом (программистом-занудой), можно в конец цикла for на рис. 6.24 вставить оператор break if Поделили = ”нет”, прерывающим выполнения цикла for. Если рыбаков будет не трое, а больше (тридцать три рыбака, например – задача для читателя), то этот прием существенно ускорит работу программы (см. главку «Оптимизация Mathcad-программ»).
Можно еще усложнить задачу, заставив любое количество рыбаков выбрасывать или подлавливать любое количество рыб.
Задачу о рыбаках и рыбке можно решать другим способом – перебором с другого конца: задать не начальное число рыб в улове, а предположить, что последний рыбак оставляет две рыбы (меньше не может быть), и увеличивать их число на единицу, если условия задачи не выполняются. Задача будет решаться быстрее, но минус двух рыб, а, тем более, минус 29 рыб мы не получим: «Keep if simple, stupid! – Делай это проще, дурачок!» Человеку психологически трудно спуститься к отрицательным числам в ответе, машина же делает это спокойно, без всяких предрассудков. Не дает отрицательного ответа и аналитическое решение задачи – поиск целочисленных корней одного уравнения с двумя неизвестными.
Остается рассказать о последней кнопке


Суть оператора проста: если при выполнении правого операнда возникнет ошибка, то выполняется левый операнд. Этот оператор позволяет реализовывать в Mathcad-программах метод проб и ошибок.
Автору, как только он познакомился с оператором on error, сразу захотелось испробовать его на простом примере:

Но оказалось, что объявленная таким образом функция y(х) возвращает нуль, а не единицу при x = 0. Дело в том, что система Mathcad, оптимизируя произведение, выдает нуль, если первый сомножитель равен нулю. Функцию y(х) нужно переписать по другому:
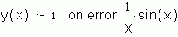
но и эта запись не совсем правомочна. Проще записать:

Оператор on error незаменим в тех случаях, когда ошибку сложно локализовать, что иллюстрирует пример на рис. 6.25.
Работа оператора on error
Здесь графически решается неравенство: функция f(x) возвращает нуль не только тогда, когда логарифм меньше единицы, но и тогда, когда делается попытка взятия логарифма от неположительного числа. Можно, конечно, решить квадратное уравнение и обойти ошибку функцией или оператором if, но на рис. 6.25 мы все сделали проще.
Поиск минимума методом золотого сечения
Аргументы функции мин_З_С:
имя функции, у которой ищется минимум (y[42]);
левое значение интервала неопределенности (a);
правое значение интервала неопределенности (b).
Функция мин_З_С возвращает значение аргумента, при котором функция y имеет минимум[43]. Он ищется циклически. Условие завершения цикла – сужение интервала неопределенности до величины, меньшей или равной значению TOL. В цикле интервал неопределенности делится в золотом соотношении, что позволяет при новом приближении к максимуму использовать данные предыдущего приближения. Это вытекает из свойств золотого сечения и позволяет в цикле вычислять только одно значение функции, а не два, как при использовании метода половинного деления (см. рис. 6.55).
Функция мин_З_С протестирована на поиске объема пожарного ведра максимальной вместимости (задача из этюда 2). Функция, связывающая объем ведра с углом вырезки заготовки, задана также программными средствами (а не вложением вспомогательных функций, как на рис. 2.2). С помощью программы поиска минимума ищется максимум за счет изменения знака анализируемой функции. Отсюда можно предположить, что одна из новых встроенных в Mathcad 8 функций ¾ Minimize или Maximize ¾ лишняя. Но это не так – в оптимизационных задачах с ограничениями (см., рис. 2.9 и 2.10) заменить поиск минимума на поиск максимума не так просто.
Поиск минимума многомерной функции
Функция minimum протестирована (рис. 6.28) на решении «четырехведерной» задачи (см. этюд 2, где решались «одно-«, «двух-» и «трехведерные» задачи – поиск оптимального посекторного раскроя круглой заготовки для изготовления одного, двух и трех пожарных ведер с максимальным суммарным объемом). Показано, что четвертое ведро лишнее (как, кстати, и третье – см. рис. 2.7).
Тестирование функции minimum на «четырехведерной» задаче
Алгоритм спуска к минимуму, заложенный в программу на рис. 6.27, ¾ простой и без всяких оптимизирующих хитростей. Так, например, при очередном приближении к минимуму лишний раз рассчитывается значение анализируемой функции в предыдущей точке. Если анализируемая функция простая и ее значение высчитывается быстро, то это повторение мало влияет на общее время поиска минимума. Но что будет, если функция достаточно сложная? Предлагаем читателям доработать программу на рис. 6.27 и исправить отмеченный недостаток. Программа должна запоминать значение анализируемой функции в предыдущей точке приближения и использовать его в новом приближении. Это, кстати, заложено в метод золотого сечения (см. рис. 6.26). А вот более сложное задание. При поиске минимума функции двух переменных мы «перекрещиваем» точку очередного приближения, как бы благословляя успех поиска:

Более оптимальная стратегия может требовать «охвата» очередной точки не крестом, а равносторонним треугольником со стороной D (симплекс-метод; при минимизации функции трех переменных точка помещается внутри тетраэда и т. д.):
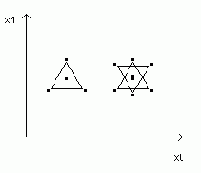
Кроме того, неплохо треугольник (либо звезду Давида или даже пятиконечную звезду – новое задание читателю) при каждом шаге приближения к минимуму ориентировать в пространстве случайным образом, растягивать его вдоль одной из вершин. Этим также можно добиться более оптимальной стратегии поиска минимума.
Описанные ухищрения можно перенести и на задачу с n переменными оптимизации (n-мерная иудейская или пятиконечная звезда!). Все это будет хорошим заданием читателям. Поиск и испытание алгоритмов оптимизации относится к одному из разделов вычислительной (прикладной) математики. В данной книге мы только чуть-чуть заглянули в него.
Читатель может отметить еще одну «неоптимальность» программы на рис. 6.27. Она генерирует не только вектор значений переменных, где функция минимальна, но и целую матрицу М с «историей» поиска, которую потом приходится транспортировать (МТ), определять номер ее последнего столбца (L) и вычленять его (М<L-1> – см. рис. 6.28). Но перегрузка программы на рис. 6.27 не была напрасна. Как уже отмечалось ранее, программирование в среде Mathcad лишено средств отладки. Простейшее, но тем не менее очень эффективное средство отладки программ – наблюдение за промежуточными результатами. А как раз это в среде Mathcad делать невозможно. И все же – если нельзя, но очень хочется, то можно. Программа, приведенная на рис. 6.27, успешно справляется с довольно-таки сложными задачами (см., например, рис. 6.28). Но если ей подсунуть совсем уж простую функцию – тестовую функцию Розенброка из этюда 3, то при определенных начальных приближениях программа на рис. 6.27 зациклится – ответа от нее не дождешься. В чем тут дело? Ответить на этот вопрос поможет некоторая модернизация программы: прервать ее работу можно не только по условию D £ TOL, но и по дополнительному условию, например, n > 30. После того как число шагов приближения n превысит 30, можно будет просмотреть след поиска минимума функции Розенброка или иной другой (задание читателю).
След при минимизации функции двух переменных
На рис. 6.29 показан след поиска минимума функции х8+y6.
Наполните ванну водой, бросьте туда перышко или какой-нибудь другой легкий предмет и выдерните пробку. Перышко сначала будет более-менее спокойно двигаться к отверстию (первый график на рис. 6.29), а затем закрутится в водовороте (второй график). Наш метод поиска минимума можно назвать не просто методом наискорейшего спуска, а методом наискорейшего спуска воды. Жидкость не просто спускается водоворотом, она всегда вращается в одну сторону. Если даже раскрутить ее в противоположном направлении, то, преодолев насилие, она снова потечет по часовой стрелке. Говорят, что это физическое явление через силы Кориолиса связано с вращением Земли: на экваторе вода в ванне не закручивается, но севернее или южнее экватора она приобретает «правый» (как на рис. 6.29) или «левый» уклон. Автор проверил эту гипотезу: он переслал по е-mail файл с задачей коллеге в Австралию. Все подтвердилось: линии траектории спуска стали закручиваться в другую сторону – против часовой стрелки. Интересно, как они себя поведут на Северном или на Южном полюсах? С водой там все ясно, она вообще не будет течь – замерзнет. А вот что будет с кривыми? К сожалению, у автора нет коллег в Арктике и Антарктике.
Читатель, наверное, уже догадался, что его разыгрывают – этот материал был опубликован в апрельском выпуске одного компьютерного журнала[45].
Но самое смешное в этой истории то, что траектории спуска, показанные на рис. 6.29 в Австралии на самом деле стали закручиваться в другую сторону. Все объяснилось довольно просто: при передаче файла на линии произошел маленький сбой и в программе на рис. 6.27 вместо строки for i Î ORIGIN .. L - 1 появилась строка for i Î L - 1 .. ORIGIN[46]. Вот и все объяснение. Но виноваты в этом все те же силы Кориолиса – магнитные диски винчестеров на серверах и маршрутизаторах Южного полушария вращаются несколько иначе, чем на Северном полушарии. Отсюда и сбои, выявить которые довольно сложно, так как при контрольной обратной пересылке файла ошибка исправляется по принципу «минус на минус дает плюс»[47].
След при минимизации функции трех переменных
На рисунке 6.30 показан объемный след при оптимизации функции трех переменных x8
+ y6 + z4.
В целях все той же отладки можно отслеживать ход поиска минимума функции четырех и более переменных, отображая проекции следа на отдельные плоскости по паре взятых переменных.
Программное решение задачи о краске: оптимизация стоимости краски
Обе программы выдают по шесть вариантов решений, лежащих вблизи максимумов объема и цены краски. Эти решения пересекаются: варианты 6/15 (шесть маленьких и пятнадцать больших) и 13/13 просматриваются в обоих решениях.
Решение задачи о компьютерах с помощью функции Maximize
На рис. 6.33 приведено решение этой задачи линейного программирования с помощью встроенной Mathcad-функции Maximize[49]. Целевые функции (ЦФ) в Mathcad-документе записаны двумя способами: общее число компьютеров (ЦФ1) как функция четырех аргументов-скаляров и стоимость компьютеров (ЦФ2) как функция одного аргумента-вектора. Это позволяет решить задачу двумя способами: «скалярным» (решение 1 по числу компьютеров) и «векторным» (решение 2 по стоимости компьютеров). Второе решение удобно тем, что его методика позволяет легко корректировать задачу: ввод новых переменных и новых ограничений требует лишь внести изменения в векторы КЦФ (стоимость компьютеров) и k (ресурсы по комплектующим) и в матрицу kC (расход комплектующих). Да, вторая методика лучше, но второе решение никуда не годится: как понимать дробные решения ¾ как призыв поставлять компьютеры россыпью или не полностью укомплектованными? Если с первым решением все ясно (можно изготовить максимум 120 компьютеров; какой стоимостью и в каком раскладе ¾ мы еще об этом поговорим), то второе нужно дорабатывать: цифры плана выпуска компьютеров нужно округлять. Дело в том, что функция Maximize не умеет возвращать решение задачи целочисленного линейного программирования. Не совсем умеют ее решать и специально созданные для этих целей программы ¾ вспомним, как в среде Excel решалась задача о краске (см. главку «Как автор продавал программы» в этюде 3).
Целочисленное решение, максимизирующее число компьютеров, получилось, можно сказать, случайно. Так же «случайно» был получен целочисленный план перевозки телевизоров со вкладов в магазины и план выпуска стульев из этюда 2.
Ничего не остается делать, как прибегать к методу перебора, плюсы и минусы которого рассмотрены в этюде 3.
Решение задачи о компьютерах перебором (максимум – стоимость)
На рис. 6.34 и 6.35 приведено решение задачи о компьютерах методом перебора. В программах реализовано три вложенных цикла – по числу типов компьютеров, максимальное количество которых подсчитать несложно: 62 штуки – С2 (лимит по комплектующему №3), 20 – С3 (по №2) и 12 – С4 (по №4). Важное замечание! В программах фиксируются все планы выпуска компьютеров, максимизирующие их число (120 штук) или стоимость (875 600 у.е. – эту цифру можно определить предварительно, отыскивая один план из многих возможных). Что дал перебор и чего не дал бы другой метод решения задачи целочисленного линейного программирования? Оказывается, планов выпуска 120 штук компьютеров целых 156. Можно выпускать не только 100 первых и 20 третьих типов компьютеров (решение, найденное на рис. 6.33), но и 75, 25, 15 и 5. Стоимость компьютеров при этом увеличивается с 560 000 у.е. до 782 500 (см. последний, 155-й столбец).
Функция Maximize «спрятала» от пользователя оптимальный план. Более того, если на рис. 6.33 в качестве начального приближения дать оптимальное первое приближение (75, 25, 15 и 5), то Maximize упорно вернет старый результат – 100, 0, 20 и 0 компьютеров.
На рис. 6.34 выведены первые и последние столбцы матрицы План, содержащей все 156 планов выпуска компьютеров общим числом 120, но с разной стоимостью: от 560000 у.е. (100, 0, 20 и 0 компьютеров разного типа) до782 500 у.е. (75, 25, 15 и 5 компьютеров).
Еще более интересное решение получается при максимизации стоимости компьютеров (рис. 6.35). Дело в том, что при решении задач линейного программирования, как правило, оперируют только неотрицательными значениями переменных (см. ограничение С ³ 0 на рис. 6.33). Но при С1<0 задача может быть сформирована с таким дополнением: «Купи на стороне компьютеры первого типа, разбери их, а дефицитные детали пусти на производство более дорогих машин». Стоимость компьютеров даже с учетом расходов на приобретение машин первого типа может быть выше, чем при традиционном решении. Так и получилось – см. рис. 6.35: матрица План содержит только 2 столбца с «нормальным» решением (1-й столбец: 1, 60, 5 и 10 компьютеров и 4-й столбец: 1, 56, 3 и 11 компьютеров). Максимальная стоимость (883 800 у.е.) получается тогда, когда на стороне покупается 27 компьютеров первого типа.
Метод перебора становится незаменим в том случае, когда задача о компьютерах перестает быть линейной. А это случается, если поставщик комплектующих делает скидку при покупке оптом. Такая динамика изменения цен нами статистически обработана – см. рис. 4.15.
Вспомогательные функции программы «Дуэль»
Участник дуэли, придерживающийся второй (хитрой) тактики, перед выстрелом в цель или перед намеренным промахом должен пересчитать противников, стреляющих лучше его. Эту работу выполняет функция Меткие. В нее заложен такой же алгоритм перебора противников, как и в функции Самый_меткий. Функции Самый_меткий и Меткие в качестве аргументов имеют вектор Меткость, вектор Статус и скаляр Стрелок. Функции при своей работе вызывают логическую функцию And (логическое И ¾ см. пункт 1) с агрументом-вектором, которая возвращает 0 (логическое «нет»), если хотя бы один из элементов вектора (аргумента) равен нулю (см. главку «Mathcad и булевы (логические) функции» в этюде 3). Для реализации математической модели дуэли нам еще понадобится функция логического отрицания Not, определяемая также в пункте 1 на рис. 6.36.
Функция Победитель (пункт 3 на рис. 6.37) возвращает номер победителя в одиночной дуэли. При этом учитывается меткость и тактика каждого участника дуэли (два вектора-аргумента функции Победитель).
Проведение дуэлей
Функция Вероятность_победы (пункт 4 на рис. 6.38) возвращает вектор, элементы которого – это отношение числа побед каждого участника дуэли к общему количеству дуэлей (третий аргумент функции Верояность_победы; два первых аргумента-вектора – это параметры дуэлянтов: их меткость и тактика), то есть вероятность победы.
Теперь, когда все необходимые функции сформированы, можно проводить статистические испытания (см. пункт 5 на рис. 6.38) и фиксировать вероятности побед участников дуэли, исходя из их меткости и тактики. Если увеличивать число побед (переменная N), то, набравшись терпения[51], можно получить результат, близкий к теоретическому.
Задача о трехсторонней дуэли приводится во многих книгах[52]. И что интересно – она там решается неверно. Априори считается, что в этой дуэли самый слабый стрелок (Джон с номером 3) имеет наихудшие шансы выжить. Но если он немного подумает (хитрая техника), то вероятность выйти победителем у него становится самой высокой (52.2(2)%).
Наше решение (см. пункт 5 на рис. 6.38) говорит о том, что у Джона и так самые высокие шансы выжить (44-46%). Начиная хитрить, он мало чего выигрывает, но подводит Билла – своего товарища по несчастью стрелять хуже Сэма.
Откуда такая ошибка в постановке задачи? Дело в том, что у дуэлянтов есть еще одна, нулевая
тактика. Если участники дуэли ничего не знают о стрелковых качествах соперников, то они бьют в первого попавшегося. Здесь вероятность побед можно подсчитать сразу без компьютера: Сэм – 43.48% (1/(1+0.8+0.5)), Билл – 34.78% (0.8/(1+0.8+0.5)) и Джон – 21.74% (0.5/(1+0.8+0.5)) или 100 - 43.48 - 34.78). Но мы составили программу и для этого случая (см. рис. 6.39).
Проведение трехсторонней дуэли (бей в случайного)
Программа 6.39 не считает вероятность побед, а скорее проверяет качество генератора псевдослучайных чисел – добротность функции rnd (см. рис. 6.40).
Статистические испытания функции rnd на трехсторонней дуэли
Задачу подправили, теперь ее можно развить.
Подсчитанная нами вероятность побед относится к ситуации, когда еще не проводилась жеребьевка по очередности выстрелов: переменная Очередь у нас либо единица, либо минус единица.
Но после жеребьевки шансы Сэма и Билла резко меняются. Дела Билла становятся совсем уж плохи (10-12%), если Джон после своего намеренного промаха передает право выстрела не ему (Очередь = -1), а Сэму (Очередь = 1). И наоборот: Сэм может потерять свои 30%, если после намеренного промаха Джона Билл будет стрелять в Сэма. У Джона вероятность победы (52.2(2)%) не зависит от очередности выстрелов.
Можно придумать и проанализировать четвертую тактику ведения дуэли: Билл и Джон сговариваются
целить в Сэма, убить его, раз он такой меткий, а уж потом выяснять отношения между собой. Инициатором такого сговора, как понимает читатель, скорее всего, будет Билл. Джон пойдет на него, если не смоделирует дуэль на компьютере и не узнает, что из этого может получиться.
Еще одно задание читателю: доработать программы на рис. 6.36-6.40 так, чтобы они были пригодны для дуэли с любым числом участников.
Наше решение задачи о трехсторонней дуэли замыкает троицу новых решений старых проблем. Две другие – задача о рыбаках и рыбке (рис. 6.24 – там мы показали, что Дирак был не прав) и основная структурная теорема (главка «Remake», где мы показали, что альтернатива ¾ это не основная, а всего лишь вспомогательная структурная управляющая конструкция программирования).
Наша модель – не такая уж оторванная от жизни. Дуэли в чистом виде сейчас, к счастью, не проводятся. Но какое-то подобие дуэли со сговором участников наблюдается на рынках, включая финансовые. Кровь там не льется, но случаются инфаркты, лопаются компании, банки, разоряются люди и даже целые страны (Южная Корея, Индонезия, Малайзия, если иметь в виду 1998 год).
Теория игр, тактика поведения участников – это не только интересная, но и очень полезная штука. Недаром в 1998 году лауреатами Нобелевской премии по экономике стали ученые, применившие теорию игр к анализу работы биржи.
И все- таки сама модель чересчур искусственна. Что такое меткость дуэлянта и как ее определить? Проводить реальные статистические испытания? Но одно дело стрелять по мишеням, а другое – целить в живого человека. На дуэлях, как правило, не убивают наповал, а ранят с различной степенью тяжести. Подстреленный дуэлянт, если хватало сил и злости, стрелял в противника (дуэль Пушкина и Дантеса, например). Попытки «приземлить» задачу о дуэлях неизбежно потребуют привлечения аппарата теории нечетких множеств (ТНМ). В этюде 3 мы уже слегка коснулись ее положений.
Меткость дуэлянта – величина нечеткая, «размытая». Никто и нигде не измеряет ее числами, а только оценивает категориями (лингвистическими константами): «мазила», «хороший стрелок», «снайпер» и т.д. Статус дуэлянта – это никакая не булева переменная. Вспомним «консилиум врачей» (из этой компании запомнилась только фельдшерица Жаба) у лежащего без чувств Буратино: «Пациент скорее мертв, чем жив», – «Нет, пациент скорее жив, чем мертв» и т. д.
Оставим дуэли в покое (да и задача уж больно кровожадная[53]) и попытаемся решить что-нибудь попроще – нашу старую задачу об оптимальном пожарном ведре (см. этюд 2).
Оптимальный радиус пожарного ведра
Пункт 1 (рис. 6.41). Матрица mr хранит представления людей об оптимальном (удобном) радиусе основания конуса пожарного ведра (r), выраженном в миллиметрах. Эти данные можно получить так: изготовить много ведер различной геометрии, дать людям поносить их и оценить по такой шкале:
удобное (1);
скорее удобное, чем неудобное (0.67);
скорее неудобное, чем удобное (0.34);
неудобное (0).
Можно принимать во внимание и другие оценки в диапазоне 0-1.
В пункте 1 мы ограничились семью точками, но их может быть намного больше: сколько людей, столько и мнений. Читатель при желании может опросить своих друзей и дополнить матрицу mr новыми столбцами.
Пункт 2. Данные опроса обрабатываются методом наименьших квадратов (см. этюд 4). На рис. 6.41 (как, кстати, и на рис. 6.42 и 6.43) в качестве аппроксимирующей кривой взята кривая нормального[59]
распределения. Получена функция принадлежности по радиусу ведра mr, которая является одним из базовых понятий ТНМ: в привычной математике считается, что некая величина либо принадлежит, либо не принадлежит определенному множеству; в ТНМ допустимо говорить о том, что величина принадлежит множеству в некоторой степени (на столько-то процентов).
Пункт 3. Статистическую обработку принято заканчивать графиком.
Оптимальная высота пожарного ведра
Пункты 4-6 (рис. 6.42) повторяют пункты 1-3, но уже для второго параметра ведра – его высоты.
Оптимальный объем пожарного ведра
Пункты 7-9 повторяют пункты 1-3 и 1-6 для третьего важного параметра ведра – его объема (веса, массы). При этом предлагается дать такие оценки:
ведро легкое (1);
ведро скорее легкое, чем тяжелое (0.67);
ведро скорее тяжелое, чем легкое (0.34):
ведро тяжелое (0).
Данные опроса также обрабатываются с использованием нормального, но уже «однобокого» распределения (см. пункт 9 на рис. 6.43).
При проектировании технических систем, конечно, не проводят опрос общественного мнения, а прислушиваются к экспертам, к лицам, принимающим решения (ЛПР).
Перевернутое» оптимальное пожарное ведро
Пункт 10 на рис. 6.44. является ядром решения задачи: в нем генерируется двухпараметрическая функция принадлежности путем слияния (перемножения) ранее заданных функций принадлежности.
В ТНМ нет понятий сложения, вычитания, умножения и др., лежащих в основе традиционной математики и реализованных в среде Mathcad операторами «+», «-», «×» и т.д. В ТНМ умножение (пересечение множеств, And) заменено на операцию поиска минимума, а сложение (слияние множеств, Or) – на поиск максимума. Математика четких множеств является частным случаем математики нечетких множеств – в программах вместо функции (оператора) And можно использовать функцию поиска минимума, а вместо функции Or – функцию поиска максимума. В среде Mathcad, кстати, нет встроенных функций And и Or[60], но есть встроенные функции min и max – это мы уже отмечали в этюде 3. В нашей задаче функция принадлежности mrh получается путем нечеткого сложения (min) функций mr, mh и mv – нечеткое множество «удобное ведро» лежит на пересечении
трех других нечетких множеств: «удобный радиус ведра», «удобная высота ведра» (пункт 6) и «нетяжелое ведро» (пункт 9).
Пункт 11. Вершина «горы» (поверхность функции mrh[61]) – это то место, где «лежит» самое удобное пожарное ведро.
Проектирование оптимального пожарного ведра
Пункт 12 (рис. 6.45). Искать максимум функции mrh в среде Mathcad можно различными способами (см этюды 2 и 3). Мы поступим так: изготовим от 2 до 10 одинаковых ведер[62] из круглых заготовок различного радиуса R (от 10 до 500 мм с шагом 1 мм). Оптимальным (самым удобным) будем считать то ведро, у которого функция принадлежности mrh максимальна[63].
Даже не очень внимательный читатель заметит неточности, допущенные при решении задачи об удобном ведре. Вот три из них:
ведро никогда не наполняется до краев;
автор уж очень вольно обращается с такими понятиями, как объем, вес и масса ведра, путая их;
не учтен вес пустого ведра, а также материал, из которого оно сделано.
Однако стоит еще раз мельком взглянуть на графики, иллюстрирующие нечеткие множества на рис. 6.41-6.43, чтобы понять важнейшую особенность решения задач с привлечением аппарата ТНМ. Наше решение вычленяет, если так можно выразиться, суть задачи, оставляя без внимания различные мелочи: плотность воды, вес пустого ведра, степень его наполнения и др.
Эта особенность в настоящее время реализована, например, в системах автоматического регулирования, где регуляторы, настроенные с учетом положений ТНМ, более «внимательны» к основному сигналу и менее восприимчивы к шуму. Оказалось, хотя это и кажется парадоксальным, что традиционные «четкие» алгоритмы управления качественно проигрывают «нечетким» либо являются их частными случаями. В теории автоматического регулирования наблюдался некий застой, так как никакие новые алгоритмы не могли сравниться со старым добрым пропорционально-интегрально-дифференциальным (ПИД) алгоритмом (законом) управления. Принципы ПИД-регулирования можно узреть в процедуре принятия решения о выдаче кредита клиенту банка, когда принимающий решение банкир учитывает, во-первых, количество денег на текущем счете просящего (пропорциональная составляющая – чем богаче клиент, тем больше денег ему можно дать в долг), во-вторых, динамику изменения текущего счета (дифференциальная
составляющая – дела клиента на подъеме или в упадке) и, в-третьих, среднее количество денег у клиента за последние, к примеру, пять лет (интегральная составляющая – не занял ли клиент вчера денег на стороне, чтобы создать видимость своего благополучия). Можно учитывать и другие составляющие, но… три – красивое число.
ПИД-алгоритм регулирования как- то незаметно был фетишизирован. Идеи нечеткого управления – это свежая струя в теории автоматического регулирования, основные положения которой в настоящее время подвергаются ревизии. Правда, есть и другое мнение. Некоторые ученые полагают, что использование аппарата ТНМ в теории автоматического регулирования и в кибернетике вообще – это попытки замены одной неопределенности на другую (шило на мыло, грубо говоря). Только и всего. Наблюдающиеся эффекты повышения качества управления скептики объясняют тем, что на регуляторы лишний раз обратили внимание (принцип доброго слова, которое и кошке приятно). Кроме того, некоторые исследователи полагают, что ТНМ (ей всего лишь 30 лет, а открыл ее миру Л.А.Заде – американец иранского происхождения) – это хорошо забытое старое. Мы не случайно перешли к задаче об оптимальном ведре от задачи о трехсторонней дуэли. По традиции, четкие множества принято иллюстрировать кругами с резко оконтуренными границами. Нечеткие же множества – это круги, образованные отдельными точками: в центре круга точек много, а ближе к периферии их густота уменьшается до нуля; круг как бы растушевывается на краях[64]. Такие «нечеткие множества» можно увидеть... в тире ¾ на стене, куда вывешиваются мишени[65]. Следы от пуль образуют случайные
множества, математика которых известна. Оказалось, что для оперирования нечеткими множествами годится уже давно разработанный аппарат случайных множеств...
Мы говорим нечеткое множество. А множество чего? Если быть последовательным, то приходится констатировать, что элементом нечеткого множества оказывается... новое нечеткое множество новых нечетких множеств и т.д. Вернемся к классическому примеру – к куче зерна. Элементом этого нечеткого множества будет миллион зерен, например. Но миллион зерен это никакой не четкий элемент, а новое нечеткое множество. Ведь считая зерна (вручную или автоматически), не мудрено и ошибиться – принять за миллион 999 997 зерен, например. Тут можно сказать, что элемент 999 997 имеет значение функции принадлежности к множеству «миллион», равное 0.999997. Кроме того, само зерно ¾ это опять же не элемент, а новое нечеткое множество: есть полноценное зерно, а есть два сросшихся зерна, недоразвитое зерно или просто шелуха. Считая зерна, человек должен какие-то отбраковывать, принимать два зерна за одно, а в другом случае одно зерно за два. Нечеткое множество не так-то просто запихнуть в цифровой компьютер с классическими языками: элементами массива (вектора) должны быть новые массивы массивов (вложенные вектора и матрицы, если говорить о Mathcad). Классическая математика четких множеств (теория чисел, арифметика и т.д.) – это крюк, с помощью которого человек разумный
фиксирует (детерминирует) себя в скользком и нечетком окружающем мире. А крюк, как известно, ¾ инструмент довольно грубый, нередко портящий то, за что им цепляются. Термины, отображающие нечеткие множества (а их достаточно в этой и любой другой книге – «много», «слегка», «чуть-чуть» и т.д. и т.п.), трудно «запихнуть» в компьютер еще и потому, что они контекстно зависимы. Одно дело сказать «Дай мне немного семечек (зерна)» человеку, у которого стакан семечек, а другое дело – человеку, сидящему за рулем грузовика с семечками.
Можно ли усмотреть некий кризис в теории и практике программирования, связанный с противоречим между четкой структурой программ (данных) и нечетким миром? Следует ли разрабатывать «нечеткие» языки программирования для реализации «нечетких» алгоритмов и для размещения «нечетких» данных? Мнения здесь разные. Программисты (а за ними последнее слово) худо-бедно научились «запихивать» нечеткий мир в строго детерминированный компьютер. Пример на рис. 6.41-45.
Перевод чисел из арабской в римскую систему и наоборот
Так было написано во втором издании книги про Mathcad 7. После выхода книги в свет автор получил решение от Артема Михайлюка, студента Киевского политеха (см. вторую половину рис 6.46). Он же прислал и совсем короткое решение – см. первую половину рис 6.47.