Работа банкомата
Операции по переводу чисел мы проводим каждый день по многу раз, расплачиваясь за покупки. Алгоритм перевода чисел может быть применен, например, в работе банкомата (см. вторую половину рис 6.47).
Окно отладки Mathcad-документа в бета-версии Mathcad 8 Pro
Можно предположить, что если курсор помещался в рамках программного блока, то выводился список локальных переменных программы и выполнялись другие отладочные операции. Но эта таблица была «мертва», а в последующих бета- и в коммерческой версиях Mathcad 8 ее совсем не стало[81].
Тем не менее потребность в отладке программ осталась, и мы о ней поговорим.
Существует две категории ошибок в программах. Ошибки первой категории связаны с неправильным обращением к функциям и операторам Mathcad, формирующим программу. Вот типичное сообщение дефектной программы: «Индексы переменной-вектора (матрицы) вне оговоренных пределов!» Вторая категория ошибок связана с дефектом самого задуманного алгоритма: программа работает без аварийных остановов, но выдает совсем не то, что от нее ожидалось.
Так или иначе, программу нужно «обезжучивать» – искать и удалять ошибки в ней. Вот семь советов на этот случай:
1. Прежде чем писать Mathcad-программу стоит «прощупать» ее основные операторы и порядок их выполнения в «беспрограммном» режиме. Мы так уже поступали, решая задачу о рыбаках и рыбке (рис. 6.22-6.24), например. А вот более «серьезный» пример. На рис. 6.49-6.50[82]
показано, как в среде Mathcad определяется коэффициент полезного действия (кпд) цикла Ренкина, где из котла в турбину поступает перегретый (острый) пар; отработавший (мятый) пар сбрасывается в конденсатор, из конденсатора вода насосом закачивается обратно в котел: так замыкается простейший цикл работы воды и водяного пара. Необходимо определить кпд этого цикла (отношение полезной работы турбины к затраченному теплу) в зависимости от его параметров: от температуры и давления острого пара и давления в конденсаторе (пункт 2 на рис. 6.49). Для расчета нам потребуются термодинамические функции воды и водяного пара: в пункте 3 делается ссылка (команда Reference… в меню Insert) на Mathcad-документ, их хранящий. Сама методика формирования этих функций (одно- и двухмерная сплайн-интерполяция) описана в этюде 4. После такой ссылки кпд цикла рассчитывается по несложным формулам, вытекающим из закона сохранения энергии.
Расчет кпд цикла Ренкина (ручной режим – начало)
Если теперь поменять параметры цикла (пункт 2 на рис. 6.49), то измениться и кпд[83]
(конец пункта 3).
Расчет кпд цикла Ренкина (ручной режим – продолжение)
Этот расчет (отлаженный и протестированный – в Mathcad-документе на рис. 6.49-6.50 выведены для контроля значения всех переменных, задействованных в расчете) целесообразно сгруппировать в функцию-программу (пункт 4.1 на рис. 6.51), по которой очень просто получить расчетные таблицы (пункт 4.3 на рис. 6.52) или графики (пункт 4.3).
Расчет кпд цикла Ренкина (функция пользователя)
При формировании функции следует не писать операторы заново, а копировать их из отлаженного документа, дабы не наделать новых ошибок.
Расчет кпд цикла Ренкина (работа функции пользователя)
Эту функцию можно использовать в новых расчетах, например, при определении реального, а не теоретического кпд реальной тепловой электростанции[84].
Если в программе есть цикл (не термодинамический, а цикл выполнения блока операторов), то его можно развернуть: дублировать операторы блока или вести расчет по этому блоку столько раз, сколько нужно. Так мы поступали, «беспрограммно» решая задачу о рыбаках и рыбке (рис. 6.22) и краевую задачу об эпидемии (рис. 5.1-5.4). Кроме того, не следует забывать о встроенных в Mathcad-функцях if и until, реализующих основные структурные конструкции (выбор и повторение) вне программ. На рис. 6.1 с помощью этих функций «запрограммирован» сложный алгоритм – поиск корня алгебраического уравнения методом половинного деления.
2. Да, в среде Mathcad специализированных средств отладки программ нет. Но они есть в других популярных программных средах: Visual Basic, Visual C, Delphi: и др. Задуманный алгоритм можно сначала реализовать и опробовать в «настоящих» программных средах, а потом уж переписать для Mathcad. Так мы поступали, решая задачу о рыбаках и рыбке (рис. 6.23 и 6.24) или составляя программы поиска корня алгебраических уравнений методом половинного деления и методом Ньютона, а также при поиске минимума методом золотого сечения. Автор задачу о трехсторонней дуэли (рис. 6.36-6.40) сначала поставил, а, главное, отладил в среде языка Visual Basic, а уже потом переписал для Mathcad, где это сразу сделать не удалось.
Воспользоваться этим советом можно лишь в том случае, если в программе нет специфических Mathcad-операторов и функций, отсутствующих в «настоящих» языках.
3. Создавая программу-функцию, на первом этапе стоит сделать так, чтобы она возвращала не только значение «одноименной» переменной, но и некоторых других, задействованных в расчете. Для этого достаточно в конец программы поставить не имя главной переменной, а какой-либо локальной, вспомогательной. Можно все переменные, задействованные в расчете, объединить в вектор и выдать их все на дисплей.
В Mathcad- программу можно вставлять своеобразные точки останова (BreakPoint): операторы return X, где X – это какая-либо локальная переменная программы. После отладки эти операторы убираются совсем или нейтрализуются таким оператором: return X if 2<1.
Если программа зацикливается и ее приходится прерывать нажатием клавиши Esc (текущие значения локальных переменных при этом просмотреть, увы, невозможно), то можно посоветовать в подозрительный цикл вставить дополнительный счетчик. Расчет будет безаварийно завершен, когда значение счетчика достигнет заданной программистом величины.
4. Если функция имеет ограниченный набор значений аргументов и/или возвращает ограниченный набор значений, то стоит не полениться и протестировать функцию глобально. Так, на рис. 3.14 в этюде 3 одноместные, двуместные и трехместные логические функции при тестировании возвращают все, что от них требовалось: у функции Not(x) два значения, у функций And(x1, x2) … AntiOr(x1, x2) – четыре значения, а у функции Решение(х1, х2, х3) – восемь.
5. Случай, описанный в пункте 4, довольно редкий. Если аргументы функции имеют действительные значения[85]
и (или) она возвращает действительные числа, то стоит проверить работу новоиспеченной функции в «экстремальных условиях» – на границах допустимых значений.
6. Вот хорошее правило: после создания программы ей нужно «подсунуть» условия задачи, решение по которым заранее известно. Так, на рис. 6.17-6.20 Mathcad-программы возвращают корни алгебраического уравнения, используя различные способы (метод половинного деления, метод Ньютона, метод секущих). Анализируемое уравнение у нас было простое: х2 - 3 = 0, корни которого известны заранее: плюс-минус квадратный корень из трех. На рис. 6.5 показаны программы решения обыкновенных дифференциальных уравнений и систем методом Рунге ¾ Кутты. Прежде чем с помощью этих функций заняться решением задачи о развитии эпидемии, мы «потренировались» на «кошечках»: рассчитали с их помощью значение основания натурального логарифма (число е).
7. Решая поставленную задачу, нужно постараться разбить ее на отдельные блоки и оформить их в виде отдельных коротких программ[86]. Это позволит локализовать ошибку и облегчить ее поиск. Объемная Mathcad-программа, в которую вкралась ошибка (ошибка алгоритма или ошибка в использовании инструментов Mathcad) – это что-то неисправимое ¾ «вещь в себе». Так, решая задачу о трехсторонней дуэли (рис. 6.36-6.40), мы выделили в отдельные функции такие действия стреляющего, как определение самого меткого противника и пересчет противников, стреляющих лучше[87]. Эти функции были протестированы и только потом стали вызываться из основной программы.
Разбивать на отдельные блоки программу целесообразно не только для оформления в функции, но и просто для отладки, для конструирования. Mathcad в этом отношении обладает уникальными возможностями: отдельные блоки программы (тело цикла, плечи альтернатив) из программы можно изъять и расположить вокруг. На рис. 6.53 изображена «разъятая» программа поиска минимума методом золотого сечения (ее рабочий вариант см. на рис.6.26). В самой же программе остались «местодержатели» (placeholder).
Разъятая Mathcad-программа
Программы можно не только «обезжучивать» (отлаживать), но и «нажучивать». В стародавние времена, когда программы в ЭВМ вводили не их авторы, а девочки-перфораторщицы и готовые тексты программ из-за этого содержали много «глупых» ошибок типа 5 вместо S, 1 (один) вместо I («и» латинское) и т.д., практиковался (больше, конечно, в теории, а не на практике) довольно оригинальный способ отладки по принципу «клин клином вышибают». Если нужно было узнать, сколько в программе осталось «жучков», то в нее... вводили еще сотню ошибок. Затем другой человек эту программу отлаживал. И если оказывалось, что он, к примеру, выловил 50 специально введенных ошибок и 10 первоначальных, то с определенной долей вероятности можно было считать, что в программе осталось еще с десяток «натуральных» жучков-ошибок. Кстати, подбор искусственных ошибок – это и наука, и искусство высокого класса, а сам процесс отладки очень трудоемкий, способный довести программиста до белой горячки. Недаром по-английски to go bugs означает сойти с ума. Очень часто бывает проще стереть написанную программу и ввести ее заново, чем искать в ней ошибки. Один коллега автора долго не мог понять, что происходит в такой коротенькой цепочке операторов:
a := 3 b := 1 a - b= -3
Если от трех отнять единицу, то должна выйти двойка, но никак не тройка, да еще с минусом? Ответ оказался прост, но эта простота была уж точно «хуже воровства». Дело в том, что в приведенном примере не b вычитается из a, а переменная a умножается на минус b. В среде Mathcad начиная с 7 версии, если константа умножается на переменную, то знак умножения можно опускать. Этот прием особо удобен при вводе размерностей 5m, 3 kg и т.д. – человек еще до общения с компьютером привык не ставить тут знака умножения. В вышеприведенном примере сначала было записано 3 b=, но потом тройку заменили на переменную a, а b на минус b. Услуга Mathcad (программисту не нужно вводить знак умножения) здесь оказалась «медвежьей». Вот еще иллюстрации принципа «Не верь глазам своим!»:
MT – что это? Транспонированная матрица M или матрица (вектор, скаляр) M в степени T?
Аi ¾ это i-й элемент вектора А или i – это часть имени переменной с текстовым индексом (набираем A.i, получаем А i)?
В переменной Стрелок первая буква английская «си» или русская «эс»?
Свести с ума может и такая «первоапрельская» шутка. Программист на минутку отлучился от компьютера, а «шутник» вверху Mathcad-документа, на правом, невидимом листе написал sin(x):=cos(x), e:=p или что другое из области «crazy[88]». Можно у отдельной переменной незаметно поменять шрифт с Variable на User1, например – эффект тоже будет очень интересным. В таких ситуациях не стоит пытаться отыскать ошибку – лучше начать все с «чистого листа»: создать новый пустой рабочий документ и в него постепенно переносить отдельные фрагменты «сумасшедшего» Mathcad-документа, отлавливая ошибку…
Поиск корня методом прямого перебора
Не трудно подсчитать, сколько раз в программе на рис. 6.54 вызывается функция y(x) – считать не будем, а просто скажем, что очень много. Наша тестовая функция (см. пункт 6 в главке «Отладка Mathcad-программ») простенькая и компьютер обрабатывает ее за микросекунды[90]. Но что будет, если функция сложна, отображает математические модели реального мира и работает довольно долго? Тут пригодится метод половинного деления (метод Ньютона, метод касательных и др. – см. программы 6.16-6.21). Если поиск корня методом перебора требует N вычисленных значений анализируемой функции, то метод половинного деления – всего лишь log2N.
Методом половинного деления[91]
можно искать и минимум функции на отрезке a-b (рис. 6.55):
Поиск минимума функции методом половинного деления
В программе на рис. 6.55 значение анализируемой функции в цикле высчитывается дважды – чуть левее и чуть правее середины интервала неопределенности. При реализации метода золотого сечения (рис. 6.26) для поиска минимума значение анализируемой функции в цикле высчитывается всего лишь раз, но сама программа становится несколько сложнее. Но если необходимо найти глобальный (самый минимальный) минимум полиэкстремальной функции на отрезке a-b, то ничего, кроме метода перебора, здесь не применить. Желательно при этом делить отрезок неопределенности не на равные доли, а случайно, реализуя метод случайного поиска (рис. 6.56):
Поиск минимума функции методом случайного поиска
2. Один и тот же результат на компьютере можно получить разными путями. Но эти пути могут занимать разное время. Автор для оценки времени работы программ использует пользовательскую встроенную функцию GetTime(a). Эта функция возвращает время (в секундах), представляющее собой разницу между системным временем компьютера и значением аргумента функции GetTime[92]. Таким образом можно количественно оценить время выполнения отдельных Mathcad-операторов. С этой функцией можно проводить эксперименты и наметить некоторые пути оптимизации программ (темы лабораторных работ по программированию).
Замена произведения возведением в целую степень
На рис. 6.57-6.59 введутся простейшие действия: числа перемножаются – число возводится в n-ю степень; числа складываются – число умножается на целочисленную константу. Результаты, как и следует ожидать, одинаковые, но время их достижения разное.
Хронометраж вложенных циклов
На рис. 6.60 с помощью Mathcad рассчитывается сумма номеров строк и столбцов. Вывод: при организации вложенного цикла необходимо «запихивать внутрь» циклы с большим числом параметров. Дело в том, что внешний цикл организуется всего лишь раз, а внутренний – по числу значений параметра внешнего. На организацию (активизацию) цикла нужно время – отсюда и экономия.
Примем оптимизации, использованный на рис. 6.60 можно назвать постановкой матрицы «на попа»: если считать, что во внешнем цикле перебираются столбцы, а во внутреннем – строки, то формируемая матрица должна «стоять торчком» – в ней 3 столбца и 100 000 строк, а не наоборот.
Существенно ускорить работу программ можно за счет чистки циклов: «Не откладывай на завтра то, что можно сделать сегодня (послезавтра) – не делай в цикле то, что можно сделать до (после) цикла!» Из циклов (да и вообще из программ) целесообразно убрать все комментарии (у нас это текстовые константы), поместив их, например, в голове программы (см. рис. 6.57) либо правее зоны программы. Если в цикле делается ссылка на элемент вектора или матрицы и эта ссылка в цикле не меняется, то лучше этот элемент массива скопировать в скаляр до входа в цикл. Тело циклов, особенно вложенных, – это главное поле оптимизации: любая экономия здесь отзывается сторицей.
4.Разбивка программы на отдельные подпрограммы повышает ее читабельность (см., например, рис. 6.36-6.40), но одновременно увеличивает время прогонки. Отсюда вывод: в отлаженной программе для ускорения ее работы можно ссылки на подпрограммы (функции) заменить на сами подпрограммы. Особый выигрыш во времени счета достигается в программах, где ссылаются на подпрограммы (функции), записанные в других Mathcad-документах, хранимых на диске (см., например, рис. 6.49).
5. Большие массивы данных можно записывать либо в виде объемных векторов и матриц (см., например, рис. 4.10 и 4.13 в этюде 4), либо в виде файлов на диске, данные из которых считываются операторами READ и READPRN. Выбор того или иного способа хранения данных влияет и на читабельность программы и на скорость ее выполнения. Отсюда вывод, который читатель сделает для себя сам. Автор же, заканчивая эту главу, должен признаться, что три вышеотмеченных приема оптимизации Mathcad программ и другие, подобные им– это «ловля блох». По-настоящему оптимизировать программу можно, отказавшись от написания ее средствами Mathcad, и перейдя к программированию на языках не интерпретирующего, а компилирующего класса. Но при этом закроется доступ к специфическим Mathcad-функциям и операторам.
[1] В восьмой версии Mathcad новых инструментов программирования не появилось.
[2] Они остались в последующих версиях для совместимости с более ранними версиями и для тех пользователей, кто к ним привык. Правда, в мастере функций Mathcad 8 (см. рис. 1.28) функции until уже нет.
[3] На рис. 6.1 элементы векторов а и b выведены для контроля правильности решения задачи, что нередко приходится делать в целях отладки
программ (см. также рис. 6.29 и 6.30, где след поиска отображен на графиках – двух- и трехмерном).
[4] Язык Mathcad, развиваясь в седьмой версии, стал все больше приобретать черты языка С. Здесь нет ничего удивительного, так как сам Mathcad писался на этом языке.
[5] VBA – Visul Basic for Applications.
[6] В Mathcad-программе поиска корня функции методом Ньютона (см. рис. 6.17) читатель может увидеть дифференциал в его общепринятом обозначении. Таким же образом в программы записываются интегралы, суммы, произведения и т.д.
[7] Первое выражение (Pascal) содержит явную синтаксическую ошибку, второе – нет, так как на языке BASIC – символ «=» означает не только присвоение, но и булеву операцию «эквивалентно». В среде языка С программист написал бы А = А == В + С, а на языке Pascal . А := А = В + С.
[8] В седьмой и восьмой версиях Mathcad оператор вывода числового значения «=» автоматически (SmarOperator) превратится в оператор присвоения «:=». Но это умолчание можно отменить.
[9] Цикл по-другому еще называют итерацией. Вот что написано в статье «Итерация» одной занимательной энциклопедии: «см. итерация».
[10] Для ускорения счета рекомендуется убирать из программ комментарии, хотя бы из тела цикла. Компилятору нужно время не только на выполнение оператора, но и на то, чтобы понять, что данный оператор выполнять не следует.
[11] Ключевые слова begin и end в среде языка Pascal отмечают начало и конец программных блоков.
[12] По TV крутятся рекламные ролики: «Нашим школам не хватает учебников. Наши детские дома требуют ремонта. Пожалуйста, заплатите налоги!» Здесь уместно будет добавить: «Пожалуйста, не воруйте бюджетные средства!»
[13] А мы знаем, что в среде Mathcad число и текст – это информация одного типа Variant. Поэтому их можно объединять в векторы и матрицы.
[14] Для этой же цели на одной строке программы мы записывали несколько операторов, разделяя их пробелами. Пробел ставится так. Сначала операторы разделяются запятыми (так было возможно разделять операторы в седьмой версии Mathcad), а потом запятые стираются. При этом появляются круглые скобки, которые можно оставить, а можно убрать. Размещение нескольких операторов на одной программной строке, как и комментирование программ текстовыми константами – это недокументированные приемы, поэтому их по возможности лучше не применять (см. также рис. 6.26). Даже вне программ нужно стараться размещать операторы столбиком. Иначе пользователь Mathcad (особенно начинающий) часто будет сталкиваться с ошибкой размещения следующего оператора чуть-чуть выше предыдущего, что нарушает причинно-следственную связь.
[15] Такую задачу в свое время успешно решал на языке BASIC К.Лапинг (рубрика «Человек и компьютер» журнала «Наука и жизнь»), которую автор в свое время редактировал вместе с Ю.В.Пухначевым.
[16] В период между Рождеством и Крещением. Программа на рис. 6.9 написана автором (вернее, подправлена для Mathcad 8) 11 января 1998 года. Так что здесь все в порядке.
[17] Здесь более уместен цикл с постпроверкой, но его нет в среде Mathcad.
[18] До Mathcad 7 Pro их тип был вещественный и при необходимости комплексный. В седьмой и восьмой версиях тип переменных – Variant (помесь числа с текстом), если исходить из стандарта языка Visual Basic и технологии OLE.
[19] Слово Pro (professional) фигурирует в названии самой современной версии Mathcad – Mathcad 8 Pro. Но в нашем контексте (см. выше) оно является латинским словом «за». Хотя слово Pro в названии пакета можно считать и некой агитацией в пользу Mathcad.
[20] Такое было возможно в ранних версиях языка BASIC, где допускались длинные переменные, но они идентифицировались только по двум первым символам.
[21] Некоторые полагают, что лет через 10-20 мы перейдем к написанию русских текстов латиницей: sejchas tak pishut teksty mejdunarodnych telegram. Молдавия, Азербайджан и некоторые другие страны СНГ уже перешли от кириллицы к латинице. Основная причина в сфере информатики. Вспомним, какие абракадабры нередко приходят к нам по e-mail.
[22] У алхимиков есть символ: «Змея, глотающая свой хвост», который подходит и для рекурсии – маленькая программа, заглатывающая память компьютера.
[23] Автор зкладывает в книгу ошибку 2000-го года: если описанному правилу будет следовать читатель в 2001 году, например, то он неверно вычислит значение данной константы – 2.719.
[24] Кстати говоря, факториал отрицательных чисел не такая уж полная чушь. У факториала (оператор целочисленного неотрицательного операнда) есть вещественный «родственник» – гамма-функция (она есть в среде Mathcad), которая работает и с отрицательными нецелыми аргументами. Значение гамма-функции при целых отрицательных значениях «улетают» в плюс-минус бесконечность.
[25] Тема чисел Фибоначчи неисчерпаема. В США даже издается специальный журнал «Fibonacci Quarterly» (электронная версия: http://www.math.uga.edu/~andrew/Fibonacci/fibauthor.html).
[26] Тройки и семерки, как автор уже отмечал неоднократно, пронизывают Mathcad.
[27] Увлекающимся числовыми последовательностями можно рекомендовать через Internet зайти на сайт www.research.att.com/~njas/sequences и воспользоваться функцией lookup. После этого можно вводить фрагмент любой взбредшей в голову числовой последовательности и ждать ответа – вариантов продолжения этой последовательности, правда, только односторонних.
[28] Еще один «долгожитель», иллюстрирующий рекурсию в книгах по программированию.
[29] Подобные задания получают студенты автора, желающие досрочно сдать экзамен по «Информатике».
[30] Слегка косят две наши милые современницы – актрисы Татьяна Шмыга и Людмила Максакова.
[31] Который, например, что-то «позаимствовал» у другого программиста, но не признается в этом даже в суде.
[32] Если единицы физических величин не используются, то нужно их совсем отключить (окно Unit System, вызываемое командой Options в меню Math).
[33] У слова «догма» есть не только отрицательный, но и положительный оттенок. Без догм не обойтись в процессе воспитания и обучения.
[34] Можно использовать и другой критерий завершения цикла: значение анализируемой функции становится меньше значения заданной точности. Так было сделано в документе на рис. 6.1 и так задумано в стандартной функции root (см. рис. 3.1).
[35] В программу на рис. 6.18 вместо «безоперандного» оператора break можно вставить оператор return, что позволит убрать последнюю строку программы с указанием локальной переменной, чье значение программой возвращается. Хотя переменную можно убрать и в программе на рис. 6.18 с оператором break. Но есть хорошее правило, не полагаясь на умолчание (программа Mathcad всегда возвращает значение последнего присваивания), дополнительно фиксировать имя возвращаемой переменной (сравните окончания программ на рис 6.17 и 6.18).
[36] Программистам-ортодоксам, раз и навсегда исключившим метку из своего арсенала, можно посоветовать наложить на себя еще одну епитимью – писать программы без использования оператора if, опираясь только на цикл while и помня, что альтернатива с одним плечом – это цикл, тело которого выполняется либо раз, либо ни разу. Предлагаем читателю для начала исключить оператор if из программ этой книги. Пример – рис. 6.20 и 6.21.
[37] Многие программисты причисляют к основным структурным управляющим конструкциям и вызов функции, особенно, рекурсивный: числа Фибоначчи без рекурсии подсчитать можно (рис. 6.11), а числа Аккермана (рис. 6.13) – затруднительно.
[38] Метод последовательных приближений широко используется в инженерных расчетах. Если блок операторов, по которым рассчитывается новое приближение, объемный, то можно рекомендовать «опустить» оператор задания первого (предыдущего) приближения к оператору вывода значения очередного приближения, записав там Ответ?50 (если говорить о программе на рис. 5.22). Это исключит «ползанье» по Mathcad-документу.
[39] Структурная революция началась со статьи Э. Дейкстры «Programming without GOTO». Сейчас многие программисты-снобы, как нами уже отмечено, хвастают тем, что они написали не одну сотню программ, ни разу не обратившись к метке.
[40] В языке Visual Basic оператора Print тоже нет, а есть метод Print.
[41] Программы на рис. 6.26 и 6.27 были написаны для Mathcad 7, где не было средств оптимизации.
[42] Предполагается, что анализируемая функция y(x) на отрезке a-b непрерывна и имеет один минимум – представим себе веревку, протянутую между двух столбов. Оптимизация такой функции – типичная инженерная задача. Пример: самолет имеет минимальную (взлет и посадка) и максимальную скорость полета (рывок перехватчика); между ними «провисает» крейсерская скорость с минимальным расходом горючего на километр пути.
[43] Вернее, возвращает среднее арифметическое от a и b, когда отрезок между ними становится меньше TOL и одновременно накрывает точку минимума.
[44] Их четыре в двухмерной задаче, 6 в трехмерной и т.д.
[45] Первоапрельский выпуск (1997 г.) еженедельника «КомпьюТерра», который назывался «КомпьюМорра».
[46] Здесь записано ORIGIN, а не просто 0 (нуль) для того, чтобы не быть привязанным к текущему значению системной переменной ORIGIN.
[47] Попытка продлить шутку.
[48] Если иметь в виду плановое хозяйство, то «выделено».
[49] Подобные задачи мы решали в этюде 3.
[50] Хорошее правило: никогда не оставляйте в теле цикла с параметром один оператор, дополняйте его хотя бы комментарием, чтобы зафиксировать начало и конец блока операторов, составляющих тело цикла.
[51] Автор оставлял на работе включенный компьютер на выходные, а в понедельник утром считывал результат прогонки модели при N:= 1000000.
[52] Смотри ссылку в конце рис. 6.38; кроме того, эта задача есть в сборнике задач по программированию для школьников.
[53] Вариант для дам: дуэлянты стреляют не пулями, а шариками с краской. Есть такая игра под названием Paintball («красящий шарик») – участники носятся друг за другом со специальными пистолетами, оставляющими яркие пятна на одежде соперника.
[54] Многие исследователи сетуют на то, что компьютер, обрабатывая эксперимент, отдаляет (и даже отделяет) их от объекта исследования.
[55] Причин, почему у современных медицинских термометров на жидкокристаллический дисплей по-прежнему выводятся не слова, а числа, несколько. Главная, по-видимому, в том, что цифры во все времена были и будут вне языкового Вавилона прошлого и современного мира (информационное эсперанто) – они понятны и европейцу, и китайцу, и арабу независимо от их образовательного уровня. Но тот же европеец, китаец или араб, глядя на термометр, видит не цифры, а диапазоны: нормальная, повышенная и т.д.
[56] Пример нечеткого множества, кочующий из одного учебника по ТНМ в другой.
[57] Эта «анафема» коснулась и Mathcad, в среде которого метки нет (см. выше).
[58] Узкое и длинное ведро будет при носке волочиться по земле, а широкое – задевать за ногу. Понятия «удобно» нет в классической математике, но в ТНМ оно узаконено.
[59] Норма – это тоже из области теории нечетких множеств. Кто-нибудь по-настоящему задумывался, почему нормальное распределение называется нормальным?
[60] Их при желании можно создать – см. этюд 3.
[61] Она похожа на перевернутое и слегка помятое пожарное ведро.
[62] Здесь учитывается удобство уже не потребителя, а производителя пожарных ведер – круглая заготовка раскраивается без обрезков.
[63] В конце аллеи участка, где расположена дача автора, стоит пожарный щит. После определения параметров оптимального пожарного ведра автор не поленился – взял в руки линейку и пошел обмерить реальное пожарное ведро на щите. Но ведро, как и все остальное (топор, лом, багор и пр.) оказалось нарисованным на щите (виртуальный пожарный щит – «отмазка» от пожарной инспекции – в каморке папы Карло висел подобный котелок над очагом).
[64] Автор не устает повторять своим студентам, что в реальной жизни есть два нечетких множества: множество вакантных мест на рынке труда и множество людей, ищущих работу. Говоря языком математики, можно сказать, что эти множества пересекаются, но отнюдь не совпадают. Цель образования, кроме, конечно, получения удовольствия (см. комментарии к рис. 6.9), – это процесс попадания в область пересечения данных множеств.
[65] В этюде 3 на рис. 3.6 мы нарисовали что-то подобное – черный круг точек, случайно и равномерно расположенных в квадрате. В квадрат можно было «кидать» точки по иному закону распределения, например по нормальному. Так можно визуализировать нечеткое множество.
[66] Эксперимент не совсем чист – женщинам приходится вынашивать, рожать и воспитывать детей, что, конечно, отвлекает от научного и художественного творчества.
[67] Более-менее «приличные» дамские романы («Сага о Форсайтах», «Анна Каренина» и др.) написаны, кстати, мужчинами – Джоном Голсуорси и Львом Толстым.
[68] В момент завершения работы над этой книгой в продаже появился «черный» лазерный диск «Mathcad 8 Pro с документацией на русском языке». Но это был двойной обман: а) на диске была, естественно, ворованная копия Mathcad и б) документацией оказалась отсканированная или украденная в издательстве мягкая копия книги В.П.Дьяконова по Mathcad 7.
[69] Говорят, что играть на фортепьяно очень просто. Достаточно нажимать нужную клавишу в нужное время. Мы это подчеркнули еще в этюде 3, когда обсуждали «художества» на компьютере. Гениальных же пианистов единицы потому, что Создатель не в силах обслужить всех играющих. Проблемы трудолюбия музыканта (программиста) мы касаться не будем, отсылая читателя к «Моцарту и Сальери» Пушкина, где эта тема разработана достаточно глубоко.
[70] В английском языке нет такой путаницы – там пишут Copyright – права на копирование. У нас же этот термин переводят неправильно – «авторские права».
[71] Здесь могут быть не потери, а прибыли. Тот же автор, написав новый труд, может получить за него гораздо больше, если он известен в читающем мире не в последнюю очередь и через нелегальные копии. Примеры: Булгаков, Высоцкий, Пастернак, Бродский… Последние двое вряд ли получили бы Нобелевские премии, если б их в свое время издали массовыми тиражами.
[72] О великий и могучий!.. В одном предложении семь аббревиатур, но иначе не скажешь.
[73] Можно дать голову на отсечение, что у писавших обличительные статьи на компьютере хоть одна из программ (DOS-Windows-Word или DOS-Лексикон) стоит нелегально. Многие милицейские отделения оборудованы компьютерами (документация, базы данных и т.д. и т.п.), но опять же можно дать что угодно на отсечение, что ни в одном отделении, включая и то, из которого был организован рейд на компьютерные рынки, вы не увидите коробок с легальными версиями программ. Милицейские чины часто по телевизору комментируют криминальную сводку. На втором плане, как правило, компьютер – тоже, мол, не лыком шиты. На экране – две голубые панели NC. Ворованные, кстати говоря.
[74] В магазине концерна « Белый ветер» на Никольской улице в Москве висит плакат: татуированная рука накрывает мышку компьютера, а сверху надпись: «Не воруй!» Автор прошелся по магазину и посмотрел цены на ноутбуки (специализация концерна). Так вот, если надбавка к цене составляет 20-30%, то ее называют торговой, а если 200-300%, то – бандитской. На Западе цена самого дорогого ноутбука 2500 долларов. Дороже может стоить только какой-нибудь спецзаказ с перламутровыми клавишами. Купить ноутбук за 5000 «косых» да еще и полное программное обеспечение к нему может только тот, чья рука изображена на плакате, смысл которого после экскурсии по магазину меняется.
[75] Упоминавшееся московское отделение знаменитой фирмы, с одной стороны, борется с пиратством, а с другой – его косвенно поощряет. Один коллега автора купил там для фирмы, где он «халтурит», легальную копию офисной системы за 2500 долл., хотя на лотках ее продают за 90 рублей. При установке программы понадобилась консультация. Звонят продавцу, а он отвечает, что перепоручил послепродажную поддержку программы другой фирме. Звонят туда. А там отвечают, что у них консультации платные – 60 долл. за вопрос. За такие деньги они консультируют, естественно, всех подряд, а не только легальных пользователей.
[76] Сексуальный аспект проблемы, если хотите.
[77] Аналогия здесь и в том, что и тот и другой мешают жене и мужу (программе и пользователю). Настоящим же пиратам все нипочем – и пояс верности, и электронный ключ ломаются довольно просто. Еще одна параллель: беспорядочный секс и нелегальное копирование программ – это главный путь распространения вирусов, человеческих и компьютерных.
[78] См. главку «Как автор продавал программы» в этюде 3.
[79] Автор познакомился с такой практикой, учась (хорошему и плохому) в Германии. Там нередко ставят программу одной установки на много машин, но одновременно просят на это разрешение фирмы-изготовителя. Фирма дает на это добро, идя навстречу университету (где еще можно так успешно рекламировать свою продукцию) и понимая, что в случае отказа программы все равно поставят.
[80] Как сказать. Этот этюд самый объемный в книге. К помощи Mathcad часто обращаются те, кто не может или не хочет работать с чистыми языками программирования. Но постепенно эти люди втягиваются в программирование в среде Mathcad и по необходимости переходят к «серьезным» языкам.
[81] Можно только предположить, что отладчик фирма MathSoft приберегает для «этапной» версии Mathcad – Mathcad 2000. Сейчас как из рога изобилия посыпятся программные продукты с приставкой «2000».
[82] Здесь мы отказались от обрамления отдельных операторов серым фоном.
[83] Принцип «Щелкни кобылку по носу – она махнет хвостом».
[84] Что с успехом делают студенты автора при курсовом и дипломном проектировании.
[85] С точки зрения чистой математики действительных значений даже в узком диапазоне неограниченное количество. В среде Mathcad и в других программных средах действительных значений переменных конечное число.
[86] У фанатов языка APL (у «апиэльщиков») есть неписаное правило – программа должна полностью умещаться на экране дисплея.
[87] Считается, что подпрограмма – это припев песни, который поют несколько раз, а в текстах песен печатают только один раз. Но отдельный элемент программы целесообразно выделить в отдельную процедуру даже в том случае, когда этот элемент работает всего лишь раз. Во-первых, так удобнее отлаживать программу, а во-вторых, эту процедуру можно вызывать из других программ.
[88] Автор при тестировании бета-версий Mathcad просил разработчиков ввести в систему жесткий запрет на переопределение встроенных функций и констант (встроенные операторы, кстати, переопределять нельзя), но это не было сделано.
[89] Из них можно сделать заставку для экрана дисплея, появляющуюся перед глазами пользователя, когда он на время задумывается и не касается клавиш компьютера.
[90] Водительское определение микросекунды: это время, прошедшее с момента появления зеленого света светофора до подачи звукового сигнала водителем, сидящим в задней машине. Микросекунда здесь не 10-6 с, а элемент нечеткого множества «очень быстро».
[91] Метод половинного деления – это универсальный метод численного решения задач. Вот его «зоологическая» интерпретация: «Как поймать льва в пустыне? Нужно ее оградить забором, перегородить пополам и посмотреть, где оказался лев. Эту половинку пустыни перегородить еще раз. Так поступать до тех пор, пока (оператор while) лев не окажется в ящике, размером TOL.»
[92] Эту функцию и описание ее создания можно «скачать» из ftp-сервера ftp:\\twt.mpei.ac.ru\ochkov\mathcad и поместить в подкаталог userefi каталога Mathcad. После этого ссылка на нее появится в окне вставки функций (рис. 1.28).
Команды символьных преобразований
Семь комментариев к примерам на рис. 7.1:
1. При символьном вычислении неопределенного интеграла (пункт 1 на рис. 7.1) и при интегрировании выражения константы опускаются (полагаются равными нулю). Отсюда такой «парадокс»: пользователь взял производную синуса в квадрате (см. рис. 7.2), а от полученного выражения ¾ первообразную. По идее должен вернуться прежний синус в квадрате, но мы получаем косинус в квадрате да еще и с минусом. Удивляться здесь можно, только если забыть тригонометрическую форму записи теоремы Пифагора (sin(x)2+cos(x)2=1) и тот факт, что при интегрировании константа принимается равной нулю.
Примеры трех основных команд символьной математики
2. Некоторые команды символьной математики требуют, чтобы перед их выполнением курсором была отмечена переменная, к которой данная команда адресуется (см. верхний предел интеграла в пункте 2 на рис. 7.1 и аргумент синуса на рис. 7.2). В меню Mathcad 7 и 8 Pro[3] в отличие от более ранних версий пакета такие пять команд (Solve – решить относительно переменной, Substitute – заменить переменную, Differentiate – дифференцировать по переменной, Integrate – интегрировать по переменной, Expand to Series – разложить в ряд и Convert to Partial Fraction – преобразовать в элементарные дроби) объединены в подменю Variable[4]. Человек привык, что x – это переменная, k – константа. Если человеку предложить найти корень уравнения a x=b, то он сразу выдаст ответ (x=b/a) без дополнительных вопросов. Mathcad таких условностей (умолчаний) не признает и требует указания переменной дифференцирования, интегрирования и т.д. В остальных случаях достаточно, чтобы все выражение было выделено курсором, как это было сделано с интегралом и дифференциалом пункта 1.1 на рис. 7.1. Можно выделить только часть выражения и применить нужную команду (например, Simplify – упростить) только к ней: было x×x+x×x, получили x2+ x×x, а не 2×x2, если перед упрощением курсором была охвачена не вся сумма, а только первое слагаемое[5]. Если правильного выделения нет, то соответствующая позиция меню Symbolic недоступна и, как это принято, прописана не черным, а серым цветом, призывающим пользователя исправить оплошность. Более опасный случай – это неверное выделение которое тем не менее, не блокирует команды меню. Так, в конце рис. 7.2 не было сделано должного упрощения из-за того, что курсор не охватил всего исходного выражения, а просто был помещен на синусе.
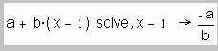
3. Если команда пункта 2 (решение уравнений) адресуется не к уравнению, а к выражению, то по умолчанию считается, что оно приравнено к нулю. Если решений более одного, то они выводятся в виде вектора. Решаться могут не только уравнения, но и неравенства. На рис. 7.3 показано, как с помощью команды Solve решается неравенство, которое мы уже пытались решить графически на рис. 6.25, иллюстрируя работу оператора on error.
Аналитическое решение неравенства
4. Команда пункта 1.2 на рис. 7.1 (вывод числового значения выражения с плавающей десятичной точкой[6]) введена в Mathcad по двум причинам. Во-первых, она позволяет делать расчеты с точностью до 4000 знаков – см. диалоговое окно Float Point Evaluation. Три точки в конце команды Float Point… (они есть и в команде Expand to Series… – разложить в ряд) означают, что перед ее выполнением последует уточняющий вопрос. В нашем случае – это точность, с которой отмеченное выражение должно быть вычислено. Обычный (не аналитический, а вычислительный) оператор Mathcad «e=» выводит основание натурального логарифма с не более чем пятнадцатью знаками в мантиссе. В пункте же 1.2 на рис. 7.1 число e вычислено с 20 знаками. Во-вторых, символьная математика пакета Mathcad оперирует некоторыми функциями, которых в самом пакете Mathcad либо нет, либо они там есть, но называются по-другому[7]. Вывести значения таких функций (на рис. 7.1 это интегральный синус Si и интегральный косинус Ci) можно через команду пункта 1.2. Объясняется это тем, что символьная математика – это не развитие пакета Mathcad, а приобретение фирмы MathSoft у фирмы Waterloo Maple ¾ у разработчика пакета символьной математики Maple V (см. раздел 7.4[8]). Отсюда некоторые нестыковки. В пакете Maple V в вычислениях возможны 64 000 (студенческая версия) и 500 000 знаков (профессиональная версия) в мантиссе[9].
5. Нередко при символьных преобразованиях из-за того, что используется чужая разработка (см. выше), ответ получается настолько не вмещающимся в рамки Mathcad (ни по форме – см. Si и Ci, ни по содержанию – число знаков), что он (ответ) не выводится на экран, а по разрешению пользователя заносится в буфер обмена Clipboard (см. пункт 1.2 на рис. 7.1, где вычислялось число p с 4000 знаками). Что с ним делать дальше, пользователь решает сам. Ответ можно перенести в среду Maple V и там «разделать», а можно попытаться вручную доработать в среде Mathcad, уточнив в help’е или в справочнике по высшей математике, что такое интегральный синус Si, интегральный косинус Ci и другие специальные функции. Нестыковки символьной математики объясняются еще и тем, что в сам Mathcad встроено много функций, которых либо нет в среде Maple V, либо они там есть, но называются или работают по-другому. Пример – функция Maximize (Minimize). В среде Mathcad она возвращает координаты максимума (минимума) функции пользователя (см. этюды 2
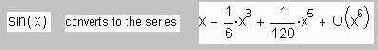
Техника аналитических преобразований с помощью команд меню Symbolic довольно проста:
пишется или откуда-то копируется исходное выражение (см. пункт 1.1 на рис. 7.1), уравнение (пункт 2) или неравенство (рис. 7.3) – делай раз;
в выражении (уравнении, неравенстве) курсором отмечается переменная (фрагмент или вся конструкция) ¾ делай два;
отдается нужная команда из меню Symbolic – делай три.
По умолчанию ответ (упрощенное или преобразованное выражение, корень, число, ряд и т.д.) появляется под исходным выражением, проталкивая вниз то, что было там записано ранее – см. опцию Vertically, inserting lines (вертикально, вставляя строки) в диалоговом окне Evaluation Style (стиль преобразований) на рис. 7.1. По такой схеме на рис. 7.1 сделано самое первое символьное преобразование ¾ взятие неопределенного интеграла от натурального логарифма. Команда[13] Evaluation Style… (последняя в меню Symbolic), вызывает одноименное вышеназванное диалоговое окно, позволяющее отойти от умолчаний в таких направлениях:
ответ можно получить ниже, но без ввода дополнительных строк (опция Vertically, without inserting lines);
ответ можно получить правее исходного выражения (опция Horizontally);
ответ может быть предварен комментарием (флажок Show Comments – см. операцию взятия производной в пункте 1.1 на рис. 7.1; комментарий системы пользователь может дополнить, сделать, например, его перевод с английского);
ответ может быть записан вместо исходного выражения (опциональный флажок Evaluation in Place).
Троица команд Упростить, Дифференцировать по переменной и Интегрировать по переменной (найти функцию, дифференциал которой – исходная функция) составляет ядро символьной математики Mathcad. Для многих студентов и инженеров этими командами (операциями) ограничивается сам математический анализ.
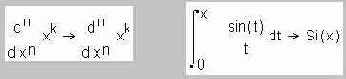
Из команд меню Symbolic заслуживают особого внимания преобразования Лапласа. Автор неравнодушен к математике[14], но любовь к некоторым ее разделам приходила с годами и с трудом. Но к операционному исчислению (в его основе лежат эти самые преобразования Лапласа) любовь пришла, можно сказать, с первого взгляда – сразу после того, как преподаватель у доски показал фокус: «накрыл» выражение шляпой преобразования Лапласа и поднял ее... Без этого раздела математики невозможно представить такие научные дисциплины, как «Теория автоматического управления», «Основы теории цепей»[15]
и др. С помощью обычных двух линеек (простейшая механическая аналоговая вычислительная машина (см. раздел 7.5), где аналог числа – расстояние) можно складывать и вычитать. Если числа нужно перемножить (поделить), то у линеек шкалы делают логарифмическими, что позволяет умножение (деление) свести к сложению (вычитанию) – ведь логарифм произведения равен сумме логарифмов сомножителей. Так устроена обычная (арифметическая) логарифмическая линейка. Преобразования Лапласа можно назвать алгебраической логарифмической линейкой. Они позволяют дифференцирование (интегрирование) заменить умножением (делением). Вот как выглядит «кругосветное путешествие» синуса (поиск производной у функции, а затем поиск первообразной у производной функции) с помощью преобразований Лапласа в среде Mathcad (рис. 7.4).
Преобразования Лапласа в среде Mathcad
Магеллан во время своего турне потерял календарные сутки. При интегрировании командой меню Symbolic (см. рис. 7.1 и рис. 7.2) константы также теряются. Кругосветное «путешествие» синуса через преобразования Лапласа (см. рис. 7.4) обошлось без потерь – исходный синус вернулся с константой С за счет того, что в промежуточных выкладках «вылезла» функция Dirac, равная бесконечности при нулевом аргументе и нулю в остальных случаях.
Команды символьных преобразований, собранные в меню Symbolic в среде Mathcad 7 и 8, Pro стали лишними[16]. Эти команды стали неким рудиментом более ранних версий (как функция until), подарком тем, кто к ним привык. Их стоит рассматривать как некие инструменты работы с базой данных по аналитическим преобразованиям (производные, интегралы, ряды и т.д.), которые в виде таблиц помещаются на первых страницах справочников по высшей математике. С одной стороны, к командам символьной математики стоит прибегать и в случае довольно простых преобразований, подобных таким, которые зафиксированы на рис. 7.1 и рис. 7.2. Дело в том, что при ручной работе неизбежны опечатки[17]. С другой стороны, элементарные преобразования следует делать самому. Это, во-первых, тренирует голову, а во-вторых... Все мы сейчас пользуемся телефонами с памятью и, звоня родным или знакомым, просто нажимаем на кнопку с именем человека вместо того, чтобы набрать номер. Все это хорошо, но если приходится звонить близким с чужого телефона, то зачастую вспомнить номер бывает трудно, а в записной книжке его, естественно, нет. Один студент автора не смог вспомнить производную от ex и побежал к компьютеру уточнить, чему она равна...
Решение дифференциального уравнения средствами символьной математики Mathcad
На рис. 7.5 командами символьной математики решается дифференциальное уравнение. Вернее, ищется одно из его решений. Полное решение можно увидеть на рис. 7.5. В конце рис. 7.5 читатель видит новый символ «®»[18], который переводит повествование от команд к операторам символьных преобразований.
Примеры работы оператора символьных преобразований
В ряде случаев оператор «®» возвращает комментарий (см. в пункте 5 ответ “undefined” – «неопределенно») при попытке вычисления предела функции 1/x без указания стороны, с которой мы приближаемся к нулю. В других случаях оператор «®» возвращает само исходное выражение (производную n-го порядка) или выражение с конструкцией, не встроенной в Mathcad, – интегральный синус, например:
Сейчас мы возьмем задачи из первых этюдов книги и по-новому их решим с помощью оператора «®».
На рис. 7.7 приведено аналитическое решение задачи о купце и сукне из этюда 1.
Аналитическое решение задачи о купце и сукне
Команда Solve из меню Symbolic годится только для решения одиночных уравнений и неравенств. Ее «численные» аналоги – функции root и polyroots. Для решения систем уравнений и неравенств предназначена функция Find, которая способна возвращать как численный, так и аналитический результат в зависимости от того, что за ней проставлено – символ «=» или «®». Во втором случае функция Find не требует первого приближения. На рис. 7.7 функция вернула Find аналитическое решение системы двух линейных алгебраических уравнений, которое было скопировано и в которое были подставлены конкретные значения переменных.
На рис. 7.8 приведен аналитический поиск минимума функции Розенброка (численное решение задачи показано на рис. 3.4), в которой константы 100 и 1 заменены на переменные a и b.
Аналитический поиск минимума функции Розенброка
Здесь через функцию Find аналитически решается система уравнений (пункт 1), собранная из частных производных функции Розенброка по x и y, приравненных к нулю.
Показано, что значение переменной a не меняет положение точки минимума – оно существенно влияет на процесс численного решения задачи, удлиняя овраг, на дне которого находится минимум. В этом можно убедиться, вернувшись к рис. 3.4 и изменив в функции Розенброка сотню, к примеру, на единицу.
Далее на рис. 7.8 в пункте 2 продолжены «деривации» этюда 3: сделаны попытки проверки на «аналитичность» двух других встроенных Mathcad-функций, также предназначенных для решения оптимизационных задач. Функция Minimize отказалась работать (пункт 2.1), а функция MinErr выдала непонятно что (пункт 2.1). Пункт 2 на рис. 7.8 – это по сути протокол экспериментов над программной средой, которые в принципе не возбраняются, но плодами которых нужно пользоваться очень осторожно.
На рис. 7.9 приведено аналитическое решение задачи о балке из этюда 1 (см. рис. 1.12, 1.15 и 1.16).
Аналитическое решение задачи о равновесии балки
Три выражения, которые вернула функция Find (пункт 1), мы использовали в этюде 1 для иллюстрации графических возможностей Mathcad (см. рис. 1.17-1.19 и 1.21-1.25).
В пункте 2 на рис. 7.9 показан и второй способ решения системы уравнений через оператор символьного преобразования с ключевым словом
(здесь ключевое слово solve – решить). Прежде чем описывать эту новую конструкцию, отметим, что в символьных преобразованиях Mathcad перестают работать встроенные единицы измерения: если оба плеча балки измеряются в метрах, то выдается правильный ответ, однако если второе плечо выражено в дюймах – ответа нет.
На рис. 7.10 приводятся образцы заготовок, которые возникают на экране дисплея в отмеченном курсором месте после нажатия клавиш панелей инструментов Evaluation и Symbolic:
Панели работы с операторами символьных преобразований
Сам оператор символьных преобразований вводится в Mathcad-документ нажатием кнопки g ® на панели Evaluation или Symbolic. После этого на экране дисплея появляется такая заготовка: g g ®. Первый операнд данного оператора – это какая-либо алгебраическая конструкция (выражение, неравенство, уравнение и др.), а второй – ключевое слово, задающее направление символьного преобразования[20]: упростить, решить, факторизировать, вычислить коэффициенты полинома и т.д. Оператор символьного преобразования с ключевым словом существенно богаче по своим возможностям команд меню Symbolic. Поэтому, как было отмечено выше, это меню фактически лишнее. Кроме того, оператор символьного преобразования сразу выдает новый ответ, если в исходном выражении что-то поменяли. Здесь не нужно стирать старый ответ, как это требуется при обращении к командам меню Symbolic.
Само ключевое слово оператора g g ® (второй его операнд) может иметь новый ключ, определяющий детали символьного преобразования. Только две команды (Simplify – Упростить[21]
и Complex – представить в комплексном виде) не имеют дополнительных ключей. Чтобы в них не запутаться, лучше не выводить на экран заготовку оператора g g ®, а поступать по-другому: записать или откуда-то скопировать исходное выражение (a+b×x=0, например) и нажать на кнопку с названием соответствующего преобразования (solve, например). После этого на экране появится уже не заготовка оператора решения уравнения, а его, так сказать, полуфабрикат: a+b×x=0 solve, g ®. В черный квадратик достаточно вставить имя переменной, по которой решается уравнение, чтобы получить ответ: -b/a. Здесь можно оперировать не только переменной, но и новым выражением – x- 1, например:
Особо хочется отметить оператор разложения на множители g factor, g ®. Если его применить не к алгебраическому выражению, а к числу натурального ряда, убрав при этом его ключ (g factor ®), то он будет называться Разложить на простые множители. Простые числа – это такие числа, которые делятся без остатка либо сами на себя (результат – единица), либо на единицу (результат – само простое число). Простые числа (2[22] – единственное четное простое число, 3, 5, 7, 11, 13, 17, 19, 23 и т.д. до бесконечности) – простые и по названию, и по определению, но за ними стоит много проблем теоретического и практического плана, одна из которых такая...
Сэм, Билл и Джон договорились... Нет, не сразиться на дуэли (см. этюд 6), а обмениваться друг с другом шифрованными сообщениями по таким правилам:
каждый i-й участник придумывает свой шифрующий (ШАi) и дешифрующий (ДШАi) алгоритмы;
шифрующие алгоритмы открыты, они известны всем участникам;
свои дешифрующие алгоритмы каждый участник держит в секрете;
если i-й участник захочет послать шифрованное сообщение j-му участнику, то он использует ШАj (он, как мы договорились, известен всем);
j-й участник, получив сообщение от i-го участника, использует ДШАj, который, как мы знаем, известен только j-му участнику;
i-й участник может послать j-му участнику шифрованное сообщение с электронной подписью[23]; для этого i-й участник, посылая сообщение j-му участнику, использует цепочку шифров ДШАi-ШАj. Получив сообщение, j-й участник читает его так: ДШАj-ШАi, восстанавливая исходный текст. При этом j-й участник будет знать, что только i-й участник мог послать такой дважды зашифрованный текст, так как при шифровании был использован ДШАi, известный только i-му участнику.
Все это выглядит просто и красиво. Проблема заключается в разработке шифрующих и дешифрующих алгоритмов. Поступим для начала так. Пусть все участники переводят свое сообщение из текста в число N (“АББА” – 01020201, например). Затем по шифрующему алгоритму Сэм возводит число в квадрат, Билл – в куб, а Джон – в четвертую степень (ША1:=N2; ША2:=N3; ША3:=N4). Дешифрующие алгоритмы (их участники должны держать в секрете) сводятся к извлечению квадратного корня, кубического корня и корня четвертой степени соответственно и в переводе полученного числа в текст. Но такая тайна будет тайной Полишинеля, так как криптоаналитику ничего не стоит, просмотрев несколько сообщений, раскрыть не только шифрующий алгоритм (а из этого никто особой тайны не делает), но и дешифрующий. Проблема создания надежных функций-ловушек
(функций, обратный алгоритм которых невозможно раскрыть, сколько ни анализируй прямой алгоритм), до сих пор полностью не решена. В криптографии пока довольствуются функциями-ловушками с «потайной кнопкой», расположение которой известно только владельцу шифра. Прятать такую кнопку можно с помощью простых чисел.
Дело в том, что сгенерировать простое число можно довольно быстро. Тем более (тем быстрее) на компьютере. Но если два довольно больших простых числа перемножить и попросить компьютер по произведению найти исходные сомножители, то эта задача окажется неразрешимой, вернее, для ее решения потребуются «миллионы лет работы самого современного компьютера»[24].
Итак, участники «шифровальной дуэли» разрабатывают шифрующие алгоритмы, используя простые числа так, что посторонний, анализируя послания, может узнать только произведение (составное число). Проблема раскрытия дешифрующего алгоритма сводится к нахождению сомножителей – к разложению числа на простые множители.
Разложение чисел на простые множители
На рис. 7.11 даны примеры работы оператора n factor ®. Если исходное число n простое, то система Mathcad довольно быстро (секунды, минуты) доказывает это и выдает один сомножитель – само исходное простое число. Короткие составные числа раскладываются на простые сомножители также за приемлемое время. Но если составное число удлинить, то Mathcad «задумывается» намертво. Не «зависает», а именно задумывается. Автор оставлял включенную машину на выходные: вместо курсора-стрелки появлялся курсор – докторская четырехуголка, что свидетельствовало о работе символьного процессора. В понедельник ответа не было, а после нажатия клавиши Esc, вызывающего диалоговое окно прерывания вычислительного процесса, и щелчку по кнопке OK работоспособность Mathcad восстанавливалась:
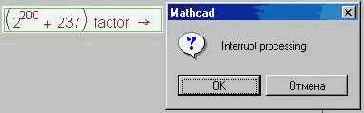
Простые числа на рис. 7.11 – это не просто простые числа, взятые наугад, а числа из различных литературных источников, где они отмечались как самые большие простые числа, известные человеку на определенных этапах развития математической науки и техники счета. Числа вида 2n-1 называют числами Мерсенна (http://www.mersenne.org). Они могут быть простыми лишь в том случае, если n – простое число (условие необходимое, но недостаточное – число 267-1 составное, хотя число 67 простое). До сих пор не доказано, имеется ли конечное или бесконечное число простых чисел Мерсенна[25]. То же можно сказать и в отношении простых чисел, состоящих только из единиц.
Особо хочется отметить число 2521-1. На рис. 7.11 показано, что это число Мерсенна – простое. Но в книге Мартина Гарднера (о ней ниже), сказано, что в 1982 году суперкомпьютер[26] «Крей» разложил его на три простых множителя за 32 часа работы. Где здесь ошибка? Либо Mathcad неправильно факторизирует числа, либо в книге Гарднера прошла опечатка (очепятка). Второе вероятнее, так как в книге отмечено, что это 69-значное число, тогда как на самом деле оно имеет больше знаков. Предлагаем читателю самому разобраться в этом вопросе. Автору тут важно поднять проблему и наметить пути ее решения с помощью Mathcad.
Для проверки чисел на простоту используют так называемую малую теорему Ферма[27] (см. пункт 2 на рис. 7.11). Если p – простое число, а число a – случайное, меньшее, чем p, то функция Ferma возвращает единицу. Если р – составное число, то функция Ferma возвращает число, большее единицы. И большая и малая теоремы Ферма пока считаются не доказанными, но если кандидат на простое число несколько раз выдерживает тест Ферма[28], то его считают «условно» простым и используют в шифровальном деле.
Я только что изложил главу «Надежные шрифты» из книги Мартина Гарднера «От мозаик Пенроуза к надежным шрифтам» (М.: Мир, 1993). После ее прочтения у меня возникло такое чувство, что либо я сам что-то недопонимаю, либо и меня и Гарднера кто-то искусно водит за нос, отвлекая от раскрытия настоящих алгоритмов шифрования.
Вот отрывок из этой книги.
«Объясняя, как работает их (шифровальная. – здесь и далее примечания автора) система, авторы из МТИ (Массачусетский технологический институт) выбрали в качестве исходного текста парафраз ремарки из «Юлия Цезаря» Шекспира (акт I, сцена 2): "ITS ALL GREEK ТО ME" («Для меня все это сущая тарабарщина» – мы говорим «китайская грамота», англичане же при этом вспоминают греков).
Прежде всего, этот текст преобразуется в одно большое число с помощью стандартного ключа: А=01, В=02, ..., Z=26 (00 – пробел между словами). Получается число 09201900011212000718050511002015001305.
Полученное число шифруется путем возведения его в s-ю степень по модулю некоторого составного числа r. Составное число r получается как произведение двух случайно выбранных простых чисел p и q, каждое из которых не менее чем 40-значно. Число s должно быть взаимно простым с числом p-1 и q-1. Числа s и r общедоступны: они используются в шифрующем алгоритме. Операция шифрования осуществляется весьма эффективно даже при очень больших значениях r; на практике она требует менее одной секунды компьютерного времени.
Два простых множителя числа r хранятся в памяти компьютера, поскольку они используются в секретном обратном алгоритме. Обратный алгоритм, используемый при дешифровке, состоит в возведении числа-шифротекста в другую степень t и в нахождении остатка от деления полученного числа на r, то есть в приведении по модулю r. Как и в предыдущем случае, на это уходит менее секунды машинного времени. Но показатель t может вычислить только тот, кто знает p и q ¾ два простых числа, которые хранятся в секрете.
Если исходный текст слишком велик для того, чтобы с ним можно было обращаться как с одним числом, то его следует разбить на блоки и каждый блок рассматривать как отдельное число. Я не буду вдаваться здесь в дальнейшие подробности. Они носят несколько технический характер и ясно изложены в отчете МТИ.
Для шифрования текста ITS ALL GREEK TO ME группа из МТИ выбрала s=9007 и r=114381625757888867669235779976146612010218296721242362562561842935706935245733897830597123563958705058989075147599290026879543541.
Число r есть произведение 64-значного простого числа p и 65-значного простого числа q, каждое из которых выбрано случайным образом. Шифрующий алгоритм заменяет число, соответствующее исходному тексту (09201...), следующим числом-шифротекстом: 199935131497805100452 31712274026064742320401705839146310370371740625971608948 927504399209626725826750128935544613538 23769748026.
Желая поощрить тех читателей журнала «Scientific American[29]», которые хотели бы испробовать свои силы на поприще криптоанализа, группа из МТИ зашифровала с помощью того же общедоступного алгоритма другой текст. Шифротекст вы видите на рис. 92 (см. книгу Гарднера). Его оригинал представляет собой предложение на английском языке. Сначала оригинальный текст был превращен в число с помощью стандартного метода, который был объяснен выше, полученное число возведено в 9007-ю степень (по модулю r) с помощью остроумного метода, изложенного в отчете. Тому, кто первым расшифрует текст, группа из МТИ обещала выплатить премию в 100 долларов.
Для доказательства того, что шифротекст действительно исходит от группы из МТИ, к нему была добавлена следующая подпись: 16717861150380844246015271389168398245436901032358311217835038446929062655448792237114490509578608 655662496577974840004057020373.
Подпись зашифрована с помощью секретного обратного шифрующего алгоритма. Так как читатель не располагает своим общедоступным шифрующим алгоритмом, вторая шифрующая операция была опущена. Каждый читатель, имеющий доступ к компьютеру и алгоритмам, опубликованным в отчете МТИ, может легко прочитать подпись с помощью общедоступных шифрующих алгоритмов группы МТИ, то есть возвести приведенное выше число в 9007-ю степень и перейти к остатку от деления на r.
Проделав эти операции, читатель получит число 06091819200019151222051800230914190015140500082114041805040004151212011819. Пользуясь стандартным ключом, читатель расшифровывает это число как FIRST SOLVER WINS ONE HUNDRED DOLLARS («первый, кто расшифрует текст, получит сто долларов»). Этот подписанный шифротекст мог быть получен только от группы из МТИ, так как обратный алгоритм, которым был зашифрован исходный текст, известен только членам этой группы.»
На этом заканчивается отрывок из книги Гарднера. Он сначала писался Гарднером по-английски, затем набирался в типографии, потом переводился на русский язык, опять набирался в типографии, затем сканировался автором для вставки в данную книгу. При такой технологии ошибки в числах текста очень вероятны. Тут вспоминается старая карикатура. Человек с перевязанными руками и ногами лежит на больничной койке, а диктор по телевизору, поставленному в палате, говорит: «Приносим извинения! В нашу вчерашнюю передачу «Делай с нами, делай как мы, делай лучше нас!» вкралась ошибка». Римейк карикатуры. «Пациент «палаты № 6» в книге по компьютерной математике читает приписку: «В наше предыдущее издание вкралась ошибка».
Автор перемножил в среде Mathcad[30]
два простых числа и поместил произведение в пункте 3 на рис. 7.1. Кто первым определит, что за простые числа были перемножены (найдет потайную кнопку шифра), получит приз, название которого также зашифровано: «Кмапвсптор к мвуепа»[31].
Оператор символьного преобразования с ключевым словом можно считать зачатком нового языка программирования, ориентированного не на вычислительный, а на аналитический процесс. Но интеграция символьной математики в среду Mathcad еще слаба и требует обилия ручной работы, без которой не составить даже функции пользователя из преобразованного выражения.
Один из коллег автора пришел в полный восторг, увидев действие пары expand – series. Ему (а он преподаватель математики в институте) по долгу службы приходится составлять вопросы для вступительных экзаменов. Ключевые слова expand – series позволяют как из рога изобилия сыпать вопросами с заголовком «Упростить», заранее имея правильный ответ. Несколько охладила этот восторг мысль о том, что абитуриенты пронесут
на экзамен ноутбук[32]
и ключевыми словами factor и simplify все эти примеры «разъяснят». Правда, на экзамене, как и в самом учебном процессе, требуется не столько ответ, сколько промежуточные выкладки... К проблеме щита и меча во взаимоотношениях ученика и учителя мы вернемся чуть позже, рассматривая место пакета Mathcad и ему подобных в процессе преподавания не только чисто технических дисциплин, но и самой высшей математики.
В среде Mathcad 8 можно вести цепочку символьных преобразований, показывая или не показывая промежуточные выкладки, которые иногда бывают настолько громоздкими, что их не то что рассмотреть – стереть с экрана бывает затруднительно.
Решение задачи о балке средствами символьной математики
На рис. 7.12 показано, как оператор solve с решает нашу старую задачу о раскрое коробки (коробок) максимальной вместимости: берется квадратная заготовка, по углам которой вырезаются маленькие квадратики. Полученная таким образом крестовина складывается в коробку (см. схему на рис. 2.4 в этюде 2). Найти параметры раскроя, дающие максимальный объем коробки. В этюде 2 мы развили эту известную школьную задачу, отметив, что из обрезков можно делать новые коробки, которых в принципе может быть бесконечное множество.
Комментарии к рис. 7.12:
В пунктах 1 (одна коробка) символьные преобразования ведутся «цугом» с выводом промежуточных аналитических выражений. Такая цепочка операторов получается следующим образом: записывается оператор дифференцирования (см. пункт 1) и нажимается кнопка оператора символьного преобразования «®» в панели Simbolic:
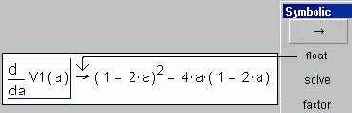
Далее ответ (производная от функции V1) охватывается курсором и нажимается кнопка Simplify в той же панели инструментов:
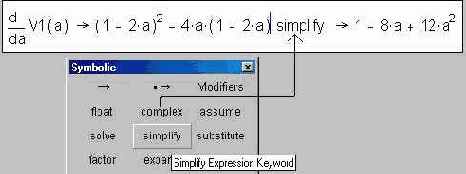
Затем к упрощенной производной прикладывается оператор решения уравнения (solve, a), возвращающий два корня, первый из которых (1/6) – ответ по задаче о коробке.
В пункте 2.1 (бесконечное число коробок с постоянной пропорцией раскроя a) символьные преобразования также ведутся «цугом». Одно из неудобств такой технологии в том, что промежуточные результаты выстраиваются по горизонтали и из-за этого их неудобно рассматривать на экране дисплея и распечатывать на бумаге принтера. На рис. 7.12 (а это, как читатель знает, «заморозка» экрана дисплея, доработанная в среде графического редактора) промежуточные выражения выстроены по вертикали, где стрелки показывают последовательность преобразований. Аналитический ответ (а численного здесь получить нельзя из-за того, что суммируется бесконечный ряд) – это вектор уже с четырьмя элементами, последний из которых (0.1736…) – решение задачи. Здесь дополнительно задействован оператор float, n, возвращающий число с плавающей точкой с n[33] знаками[34].
В пункте 2.2 операторы, решающие задачу о бесконечном числе коробок, выстроены не «цугом», а «парой», если так можно выразиться. При этом промежуточные результаты не показываются, так как они очень громоздки, и ничего не дают ни уму ни сердцу. Обычно пользователь комбинирует «упряжку» символьных преобразований, получая какое-то подобие «шестерни», когда лошади идут парами цугом.
В решении двухмерной оптимизационной задачи о пяти коробках (пункт 3 – два шага раскроя) выведены и аналитические и численные ответы (их четыре; правильный – второй).
В решении трехмерной оптимизационной задачи о двадцати одной коробке (1+4+16 –пункт 4) выведены только численные ответы (их двенадцать; правильный – восьмой сверху). Честно говоря, задача о любом числе коробок сводится к одномерной оптимизации последовательными решениями: пропорция последнего раскроя равна 1/6; зная это, можно одномерной оптимизацией найти раскрой первого шага из двух при пяти коробках и т.д. Здесь просматривается рекурсия, к которой мы еще вернемся в конце этюда.
Из рис. 7.12 видно, что символьный процессор пакета Mathcad выдает много лишних ответов. Из-за этого не только увеличивается объем Mathcad-документа, но и неизбежны сбои, когда символьная математика отказывается выполнять простейшие, на взгляд человека, операции или выполняет их не так как надо. В связи с этим в среду Mathcad введены операторы и ключи, позволяющие игнорировать (по-английски to assume) некоторые направления преобразований. На рис. 7.13 даны примеры таких игнорирований. Во-первых, пустой с точки зрения вычислительной математики оператор присваивания x:=x (пример 1 на рис. 7.13) лишает переменную x (или какую-то другую) ее численного значения. В примере 2 упрощается квадратный корень из икса в квадрате. Результат получается разным в зависимости от типа переменной x.
Игнорирования при символьных преобразованиях
По умолчанию тип всех переменных, участвующих в символьных преобразованиях, – комплексное число. Отсюда и соответствующее «упрощение» квадратного корня из квадрата – scgn(x)×x. Можно игнорировать отрицательные значения переменной (assume, x³0) и получить на самом деле упрощенный ответ – x. Ключ assume=real заставляет рассматривать все переменные в качестве вещественных (реальных). При этом можно оговорить диапазон изменения значений вещественных переменных – ключ assume=RealRange(0,¥). Ключ trig заставляет в тригонометрических преобразованиях учитывать тождество sin(x)2+cos(x)2=1.
Задача маленького Гаусса
Пакет Mathcad с выключенным режимом оптимизации (умолчание), столкнувшись с суммированием, начнет по примеру нормальных (талант – это аномалия) одноклассников Гаусса прибавлять к единице двойку и т.д.: 1+2+3+4+5+...+100. В среде Mathcad мы тоже можем написать такое длинное выражение, но проще воспользоваться оператором суммирования – см. рис. 7.14. Если в примере на рис. 7.14 увеличить значение n до миллиона, например, то время счета станет неприемлемо долгим. Если это не суммирование, а интегрирование (в руководстве пользователя Mathcad приведен пример с тройным интегралом), то это сути дела не меняет: пакет Mathcad будет по-прежнему что-то там долго и упорно суммировать[36], опираясь на соответствующий численный метод (прямоугольников, трапеций, парабол и т.д.[37]). Такие расчеты можно и нужно оптимизировать. В конце рис. 7.14 получена простая формула, которой можно заменить сумму членов натурального ряда: (n2+n)/2. Если включить режим оптимизации (переключателем Optimize в меню Math –см. рис. 7.14), то пакет Mathcad будет пытаться во всех выражениях искать упрощающие формулы и работать уже с ними, а не с исходными выражениями. Это будет глобальная оптимизация. Возможна и «точечная», локальная оптимизация, когда упрощающая формула ищется только для отдельных выражений. Для этого правой кнопкой мыши вызывается локальное меню с командами, применимыми к математическому выражению, а через него вызывается диалоговое окно свойств выражения Properties[38]. В этом окне у позиции Enable Optimization (возможность оптимизации) ставится флажок[39]. Включенный тем или иным способом режим оптимизации суммы (произведения, интеграла, дифференциала – всего, что можно заменить более простой формулой, – см. первые страницы справочников по высшей математике) заставляет систему Mathcad вспомнить о лаврах Гаусса и отказаться от лобовой атаки. Если более оптимальное решение найдено (его поиск отображается мерцанием на экране докторской четырехуголки – признак того, что работает символьная математика), то правее выражения появляется красная шестиугольная звезда[40]. Свершилось чудо – машина стала считать не только быстрее, но и умнее. Пользователь может просмотреть не только численный результат, но и аналитическое выражение, упростившее расчеты (заменившее собой сумму). Оно заносится в специальный буфер, отображаемый на дисплее командой Show Popup в локальном меню или щелчком по красной звездочке.
Программисты могут здесь вспомнить оптимизирующие компиляторы, вмешивающиеся не только в кодирование алгоритма, но и в упрощение формул. Ввел программист строку S := (A * A - B * B) / (A - B), нажал Enter, а на экране – S := A + B.
Оптимизация в задаче маленького Гаусса – это стрельба из пушки по воробьям: отрезок суммируемого ряда надо значительно увеличить, «чтобы почувствовать разницу» во времени счета. При каком значении n такая оптимизация оправдана – это новая оптимизационная задача: оптимизация, так сказать, в квадрате. Оставим ее для студенческих лабораторных работ, а сами стрельнем из пушки не по воробьям, а по... двум зайцам и покажем, что в ряде случаев оптимизация не только ускоряет расчеты, но и повышает их точность. Скажем осторожнее – влияет на точность. И не только количественно, но и качественно – за счет исправления методологических
ошибок (промахов) численных методов и их конкретных оптимизаций в среде Mathcad.
Упоминавшийся пример оптимизации интеграла из документации к пакету Mathcad тривиален – ясно, что криволинейная трапеция (сам интеграл) и набор маленьких вписанных прямоугольников (приближение к интегралу) никогда не сравняются по площади. А вот более сложный пример (рис. 7.15), показывающий двойственность процесса оптимизации.
Загадка оптимизации
Какой ответ (лобовой – 25 007 600 или хитрый – 24 999 750) правильный, сказать трудно. Автор не стал отыскивать оптимизационный алгоритм или расчетную формулу, а составил BASIC-программу и использовал ее в качестве «третейского судьи» (см. рис. 7.16). Ее запуск выдал на дисплей второе число (24 999 750), что свидетельствует в пользу «второго зайца» – оптимизация не только ускоряет расчеты, но и делает их более точными даже при работе с целыми числами. Математики, к которым автор обратился как к высшим судьям, подтвердили правильность расчетной формулы и дефектность прямого счета. Дело, по-видимому, в том, что на языке C (а на нем писался и Mathcad и Maple V) очень просто запутаться в циклах с пересекающимися параметрами, если при этом нужно оптимизировать еще и саму программу.
Dim n As Integer
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim S As Long
n = 100
S = 0
For i = 1 To n
For j = 1 To n - i
For k = 1 To n
S = S + k
Next
Next
Next
Print “Ответ:”; S
Запуск программы
Ответ: 24 997 500
BASIC-программа – «третейский судья»
Но и с BASIC-программой на рис. 7.16 не все так просто – в цикле с параметром j может оказаться и оказывается так, что n-i (конечное значение параметра цикла) становится меньше единицы (первое значение параметра цикла). В этом случае заголовок цикла должен оканчиваться оператором Step - 1. В нашей же программе шаг изменения параметра по умолчанию всегда равен плюс единице (см. также описание цикла for в этюде 6).
Рассказывая о преподавателе математики, который пришел в восторг от новых ключевых слов expand и series, до предела упрощающих составление вопросов для экзаменов, автор высказал опасение, что абитуриент пронесет на экзамен ноутбук и без труда все решит. Именно «пронесет», а не принесет. За стилистическими различиями скрывается большая проблема, связанная с принятием или непринятием компьютерной математики в преподавании школьных и вузовских дисциплин.
После того как автор стал использовать пакет Mathcad в курсе «Оптимизация химико-технологических процессов», ход занятий кардинально изменился. Раньше разбору сути научно-технической проблемы удавалось отводить не более 20% учебного времени, а остальные аудиторные часы «уходили в гудок» – тратились на разъяснение методов оптимизации и способов их реализации на языках BASIC, C, fortran. Пакет Mathcad и ему подобные перевернули эту ненормальную пропорцию: появилась возможность быстро и элегантно (у английского слова smart есть и другой перевод – «элегантно») решать поставленные задачи без кодирования алгоритма, а в естественном их представлении не только численно, но и аналитически. К программированию приходится прибегать лишь в крайних случаях, когда стандартных средств не хватает. А среда Mathcad позволяет дополнять свой арсенал новыми функциями, программируя их (см. этюд 6). Но эта работа – удел избранных. Основная масса студентов никогда серьезно программировать не будет. Учить их программированию для заполнения графика учебной нагрузки можно, но эффект от этого будет минимальным, а удовольствия никакого. Как игра на скрипке требует особого музыкального слуха, так и написание серьезных программ немыслимо без особого программистского чутья («слуха»), которым обладают далеко не все.
Сейчас в среде преподавателей живо обсуждается вопрос о месте компьютера в процессе изучения высшей математики. Реакций на появление описываемых в книге инструментальных средств две: (а) «держать и не пущать» и (б) кардинально менять методику и содержание учебных курсов. Калькуляторы ликвидировали устный счет как род занятий по арифметике. Автор, учась в начальной школе, должен был через три секунды дать правильный ответ на вопрос: «Сколько будет, если помножить 89 на 76?» Теперешним школьникам, вооруженным калькуляторами, такие вопросы могут только в страшном сне присниться. Здесь впору и сожалеть: устный счет – прекрасная гимнастика для ума. Недаром старый Болконский мучил княжну Марью алгеброй, а самые знаменитые биржевые аферисты – прекрасные математики (вспомним финансовую пирамиду из этюда 5). Есть опасение (или надежда – кому как), что средства символьной математики ликвидируют такие формы практических занятий, как поиск пределов, интегралов, разложение функции в ряд, дифференцирование и др. А это львиная доля содержания семинаров по математике.
Проблема же компьютера на вступительном экзамене по математике снимается довольно просто: если абитуриент с его помощью решит все задачи, то ему впору не пятерку ставить, а диплом выдавать.
На самом деле реакций на появление средств символьной математики не две, а три. Третья реакция определяется не отношением преподавателей к этому ноу-хау, а отношением общества к самим преподавателям. При нынешнем уровне оплаты учителям впору спасибо говорить лишь за то, что они входят в аудиторию и ведут занятия по накатанному пути и на довольно высоком уровне. О кардинальной переделке методики и содержания учебных курсов не может быть и речи. Для этого к занятиям нужно основательно готовиться[41], а времени нет: чтобы прокормить семью, надо халтурить (образчик такой «халтуры» перед глазами читателя). Да и сама символьная математика пока не так совершенна, чтобы можно было все бросить и ухватиться за нее. Тот же Гаусс в гробу перевернулся бы, если б увидел, как пакет Mathcad оптимизировал его несколько измененную школьную задачу. Оказывается, что перестановка слагаемых местами меняет сумму.
Парадокс режима оптимизации
Подобная неприятность случается и при использовании оптимизирующих компиляторов, о которых мы уже упоминали и работать с которыми нужно очень осторожно. Автор когда-то долго бился над одной программой, пока не понял, что оптимизирующий компилятор упорно выносит за рамки цикла системную переменную, считая ее константой. Ошибки вычислительной математики, как правило, понятны и простительны, ошибки же символьной математики иллюстрируются пословицей: заставь дурака богу молиться – он и лоб расшибет. Фокус рис. 7.17 в том, что там решается квадратное уравнение, у которого, как известно, два корня. В практических расчетах отрицательный корень часто отбрасывается. Его принимают за пришельца из потустороннего мира (отрицательная масса, концентрация, абсолютная температура и т.д.). Символьная математика, желая угодить пользователю, подсовывает ему один корень, но не тот, какой надо. Оба корня (100 и -101) найдены на рис. 7.17.
В Руководстве пользователя Mathcad запрещается в суммах давать верхнему пределу значение меньше, чем нижнему. В этом, наверное, заключается ключ к разгадке проблемы на рис. 7.17. Программа же на рис. 7.16 имеет циклы с положительным единичным шагом параметра, что не вполне соответствует суммам на рис. 7.15 (см. описание цикла с параметром в этюде 6).
Но шутки, тем более грубые, в сторону. Реакция «держать и не пущать» вполне обоснована. Опыт западных университетов показывает опасность подмены традиционных занятий изучением математических пакетов[42]. В процессе решения огромная роль отводится постановке учебной задачи и интерпретации результата. Освоение машинной математики может создать иллюзию освоения самой математики: студент, выполнив кучу команд и получив на дисплее массу чисел, формул и графиков, не знает, что с ними делать дальше, и не понимает, где кроется настоящее решение. Из-за этого многие преподаватели вполне обоснованно считают, что включение в уроки математики компьютера равносильно... дооборудованию спортивного тренажера гидроусилителями[43]. Другое дело старшие курсы, где математический аппарат применяется для решения конкретных научно-технических задач.
В седьмой версии Mathcad символьная математика проникла и в программирование – см. рис. 7.18.
Символьная математика и программирование
Символьная математика пока плохо стыкуется с программами Mathcad. Стоит программы на рис. 7.18[44]
слегка усложнить, как тут же появляются сообщения об ошибке. Особенно несовместимы с символьной математикой операторы if, otherwise, break, continue и return (острые углы, которые не терпит природа). В программирование Mathcad проникли пока только зачатки символьной математики из пакета. Подождем новой версии Mathcad, а сейчас обратим свои взоры к Maple V.
Путешествие» тройки в среде языка BASIC
Этот протокол показывает, что происходит манипуляция исходной тройкой сначала прямыми (степень, тангенс), а потом обратными (корень, арктангенс) действиями, в связи с чем в переменную e возвращается уже нетройка (тройка с хвостиком).
В среде Mathcad (рис. 7.20) текстовый режим ввода выражений заменен на графический. Кроме того, знак присвоения «=» заменен на знак «:=», а оператор print реализуется через Mathcad-оператор «=». Но это сути дела не меняет: тройку постигла та же печальная участь, что и на рис. 7.19.
Путешествие» тройки в среде Mathcad
Пакет Maple – это, грубо говоря, BASIC-интерпретатор, к которому «прицепили» более 2500 встроенных функций, решающих разнообразные математические задачи: поиск корней уравнений и систем, построение графиков, оптимизация, линейная алгебра, интегральные преобразования, линейное программирование, статистика, тензорный анализ, анализ функций комплексных переменных, теория графов, комбинаторика и многое другое.
Основной (а для многих пользователей – единственный) режим работы Maple – это режим немедленного выполнения команд строки. Как и в среде BASIC, они вводятся в виде текста, а двоеточие служит разделителем операторов. На экране дисплея в среде Maple по умолчанию строки ввода прописаны красным цветом, графический отклик системы – синим, а комментарии пользователя – черным. У языка GW-BASIC цветового выделения не было (впервые этот прием был использован в языке Quick Pascal, а сейчас расцвечивают почти все программы[49]). Готовность интерпретатора «слушать» очередную фразу пользователя (который постепенно переставал быть программистом) отмечалась восклицанием Ok, аналогичным слову «прием» у радистов. А вот как выглядит «кругосветное путешествие» тройки в среде Maple (рис 7.21).
Путешествие» тройки в среде Maple
Глядя на рис. 7.19-7.21, можно утверждать, что Maple – это BASIC, в котором поменяли идеологию (структуру хранения и обработки данных); а Mathcad – это BASIC, в котором изменили интерфейс. Короче говоря, Maple – это BASIC сегодня. (Сравнение, конечно, еще то! Вспомним другое: «Сталин – это Ленин сегодня». Автору в свое время набили голову всякой идеологической мурой, которая всплывает из глубин памяти в самые неожиданные моменты. Вот еще одно идейно выдержанное определение: «Mathcad – это материалистическое направление развития языка BASIC, а Maple – идеалистическое».)
Интерфейс Maple ориентирован на тех пользователей, которые уже набили руку на программировании в средах традиционных языков с вводом сложнейших формул в текстовом режиме. Для таких людей ввод квадратного корня и других математических операций с помощью нажатия соответствующих кнопок на панелях инструментов (технология Mathcad – см. рис. 1.3 в этюде 1) – чистой воды профанация. Редактирование в графическом режиме ранее введенной формулы для них часто становится вообще неразрешимой задачей. Те же, кто с пеленок вкусил легкость и удобство ввода формул в их естественной «многоэтажной» математической нотации Mathcad, морщат нос от всяких там sqrt, int, diff (корень, интеграл, дифференциал – технология Maple) и т.д. Именно на них ориентирован интерфейс Mathcad, и в этом, наверное, одна из причин его популярности. В пятой версии Maple появилась возможность ввода текстовых заготовок функций через нажатие соответствующих кнопок – см. рис. 7.21.
Роковое путешествие» тройки в среде Maple
Протокол на рис. 7.22 почти полностью повторяет протокол на рис. 7.21, только в формулах число 77 заменили на 2, а число 99 – на 3. Задачу упростили, но тем не менее исходная тройка в ней безвозвратно потеряна. Вместо нее вылезло комплексное число, на тройку совсем не похожее. Ошибки вычислительной математики искажают числа слегка (см. рис. 7.19 и 7.20), ошибки символьной математики почти всегда бывают фатальны. Но чаще приходится говорить не об ошибках, а о взаимном недопонимании пользователя и программы. Фокус рис. 7.22 состоит в том, что арктангенс – это не совсем обратная тангенсу функция, а квадратный корень из числа – это не совсем то же, что число в степени одна вторая. Еще раз повторяем, что без хорошего знания математики к Maple лучше не обращаться.
Одно время, когда персональные компьютеры были у нас новинкой, за работающим у дисплея человеком пытались наблюдать психологи. Наблюдать и делать выводы, которые, как правило, были двух сортов: психолог либо формулировал всем известную истину либо психолог изрекал явную глупость. Умный психолог выбирал третий вариант – он молчал. Что-то подобное можно отметить, анализируя работу символьной математики. Несложно придумать пример (см. рис. 7.22), на котором она «сломается» и выдаст «неправильный» результат (Mathcad и BASIC задачу на рис. 7.22 решают «правильно»). Более-менее простые аналитические преобразования выполняются вручную, и компьютер ничего нового здесь не открывает. Обычная (увы) реакция компьютера на сложные задачи – молчание (см. рис. 7.24, где показана попытка аналитического решения дифференциальных уравнений).
Решение дифференциального уравнения в среде Maple
Инструменты символьной математики Mathcad (см. рис. 7.5) позволяют найти за раз только одно из решений (без констант) дифференциального уравнения, записанного на рис. 7.23. Пользователю при этом придется поработать головой и руками, преобразуя исходное уравнение в интегральное, копируя промежуточные выкладки и т.д. Поэтому знание математики нелишне и при работе с Mathcad.
Возвращаясь к теме интерфейса Maple, отметим, что документ Maple может быть структурирован
пользователем: если щелкнуть по кнопке, расположенной левее названия параграфа, то соответствующая область захлопнется и останутся только название параграфа и кнопка – но уже не с минусом, а с плюсом внутри. Это очень удобно при работе с объемными документами. Такая технология заложена во многих Windows-приложених, например в текстовом редакторе Word. В последних версиях Maple и Mathcad допустимы гипертекстовые ссылки.
Как понимает читатель (вернее, знает из курса высшей математики), далеко не всякое дифференциальное уравнение имеет аналитическое решение, описываемое комбинацией известных математических функций и операторов, да и не всякое существующее аналитическое решение удается найти. Кроме того, очень часто аналитическое решение бывает настолько громоздким, что от него приходится отказываться, особенно если нужно найти решение в точке (задача Коши). На рис. 7.24 решается известная задача о развитии эпидемии из этюда 5. Напомним суть задачи. В городе с 22 тыс. жителей появляются 50 инфекционных больных, что вызывает эпидемию. Предположим, что прирост больных за день пропорционален (с коэффициентом Pr[52]) произведению числа здоровых (еще не переболевших и не приобретших иммунитет) на число больных. Спрашивается, как развивается эпидемия, то есть как изо дня в день (переменная t) меняется число больных (функция x) и число здоровых (y). Проблема сводится к решению задачи Коши для системы двух обыкновенных дифференциальных уравнений.
Задача об эпидемии в среде Maple
Maple решил систему аналитически. Но что с этим «решением» делать дальше?!
На рис. 7.25 представлен протокол решения в среде Maple задачи о равновесии балки (решение этой задачи в среде Mathcad дано на рис. 1.15 и рис. 1.16 в этюде 1) – поиск реакций опор x, y и Р, которое сводится к решению системы трех алгебраических уравнений, описывающих баланс сил и их моментов. Задача решается полностью на аналитическом уровне и заканчивается формированием функции y, по которой строится трехмерный график.
Задача о пожарном ведре в среде Maple
Вот некоторые отличия в идеологиях Mathcad и Maple:
Maple-документы должны начинаться с команды restart. Дело в том, что в среде Mathcad действие оператора «:=» распространяется вниз и вправо в текущем документе. В среде же Maple действие оператора присвоения распространяется не только во все стороны документа, но и на другие открытые документы. Команда restart – это своего рода «санитарный кордон», пересекающий действие ранее объявленных переменных, функций, библиотек и т.д.;
Maple более близок к традиционным языкам программирования из-за текстового режима ввода строк. Все математические кнопки Mathcad в среде Maple имеют буквенную кодировку: квадратный корень – sqrt, интеграл – int, дифференциал – diff и т.д. Нужно также помнить латинскую транскрипцию греческих букв: alpha, beta, gamma и т.д.;
при построении декартова графика в среде Maple нет необходимости указывать число точек на графике. По умолчанию их 50. Этот принцип перешел в среду Mathcad, но не полностью. Забегая вперед – к рис. 7.27, следует отметить, что в среде Maple до предела упрощена и процедура построения поверхности: достаточно сообщить имя функции двух переменных и диапазон изменения аргументов. Размер сетки (grid) и другие параметры поверхности задаются по умолчанию. В среде Mathcad построение поверхности сопряжено с предварительным заполнением матрицы значениями функции двух переменных. При этом значения аргументов терялись, вместо них появляются эрзац-аргументы – номера строк и столбцов матрицы;
в среде Maple есть функция maximize, возвращающая максимальное значение (естественно, символьное) анализируемой функции. В среде Mathcad похожее действие производит функция max, возвращающая элемент вектора или матрицы с максимальным значением.
Лобовая атака на три пожарных ведра (рис 7.27) в среде Maple не удалась (численное решение задачи на рис. 2.7).
Задача о трех пожарных ведрах в среде Maple
Минимум функции Розенброка в среде Maple (рис. 7.28) отыскивается без проблем.
Функция Розенброка в среде Maple
В этюде 3 мы решили задачу о краске – задачу линейного программирования. А вот как в среде Maple решается другая подобная задача – об оптимальном плане выпуска стульев.
Суть задачи. Мебельная фабрика может выпускать стулья двух типов – по 8 и 12 тысяч рублей. Под этот заказ выделены материальные и людские ресурсы: 440 погонных метров досок, 65 квадратных метров обивочной ткани и 320 человеко-часов. Известно, сколько досок, ткани и времени идет на изготовление каждого стула:
| Стул | Расход досок, м | Расход ткани, м2 | Расход времени, чел.-час. | ||||
| Первый | 2 | 0.5 | 2 | ||||
| Второй | 4 | 0.25 | 2.5 | ||||
| Ресурс | 440 | 65 | 320 |
Спрашивается, как нужно спланировать производство стульев, чтобы наделать их ценой поболее. Это и отображено в отчете о решении задачи на рис. 7.29.
Данная задача относится к широкому классу задач под названием задачи линейного программирования: необходимо установить план (программу!) выпуска изделий (у нас это стулья), ориентируясь на целевую функцию (общая стоимость стульев) и принимая во внимание ограничения
(ресурсы по доскам, ткани и человеко-часам).
Решение задачи о стульях в среде Maple
Для решения задачи линейного программирования в среде Maple подгружается специальная библиотека simplex. При этом появляется предупреждение (Warning) о новом содержании функции maximize. Функция inequal из библиотеки plots позволяет визуализировать решение задачи линейного программирования с двумя переменными: прямые линии отсекают лишнее и оконтуривают область существования решений (затемненная область). Решение задачи находится на одной из вершин полученного многоугольника и отыскивается модернизированной функцией maximize.
В среде Maple функция solve (решить) имеет много модификаций, определяемых префиксом. Просто solve решает алгебраические уравнения и системы, dsolve - дифференциальные и т.д.
В протоколе на рис. 7.30 функция rsolve ищет рекуррентные (r) формулы для поиска чисел Фибоначчи (см. в этюде 6 рис. 6.13 и 6.14).
Maple и числа Фибоначчи
В книге рассматриваются программы, работающие под управлением Windows. Эта операционная система позволяет интегрировать различные прикладные пакеты, а возможность перебрасывать задачу из одной программной среды в другую, избегая их отрицательных качеств и эксплуатируя положительные, – уже путь к успеху. Кроме того, не следует забывать о гибридности решения задач...
Гибридное решение задачи о пожарных ведрах
Далее делается попытка решить полученное уравнение (производную, приравненную к нулю) ¾ найти значение угла вырезки a, при котором объем пожарного ведра будет максимальным (там производная равна нулю). Пакету Mathcad такая работа окажется не по зубам: будет выдано сообщение о том, что ответ настолько «неприличен», что его стыдно показывать, а надо прятать в буфер обмена. Из буфера обмена такой специфической ответ можно перенести в Mathcad-документ текстом (для этого готовится текстовая область – нажимается клавиша «“») или числом. В тексте на макроязыке Maple зафиксирована попытка решения уравнения. Числовое решение позволяет еще раз убедиться в том, что Mathcad обладает зачатками чувства юмора: сообщается, что корни есть. Первый из них (360 градусов) можно отбросить сразу – при таком «раскрое» круглой заготовки объем не максимальный, а минимальный. Второй же «корень» (Root) иллюстрирует принцип: «каков вопрос – таков и ответ». Но если пользователь по-прежнему желает получить аналитический ответ, он должен вернуться к исходной производной и помочь пакету Mathcad решить уравнение, приняв во внимание тот факт, что если один из сомножителей равен нулю, то равно нулю и все произведение. Преобразует же исходное выражение к произведению отдельных сомножителей команда факторизации (Factor), которую мы довольно подробно рассмотрели, анализируя простые числа (рис. 7.11). На рис. 7.31 команда Factor не только нашла произведение, но и упростила выражение для производной, что позволило свести решение к поиску корней квадратного уравнения.
Аналитическая попытка решения задачи о двух ведрах (пункт 2 на рис. 7.31) оборвалась на самом первом шаге – на попытке взятия производной. Но решение у задачи есть, и автор предлагает читателю найти его гибридным методом, комбинируя число, символ и интуицию.
На рис. 7.32. представлено решение задачи о бесконечном числе коробок (см. схему раскроя в пункте 1 на рис. 7.15) с бесконечным числом пропорций выкройки, найденное безо всякого компьютера Б.С. Кушнером из г. Жигулевска Самарской области.
Гибридное решение задачи о коробках
Вторая сторона проблемы повернута, как это ни покажется странным, из области науки в область искусства и даже религии.
Есть люди, способные настроиться на определенный лад, вспоминая любимые стихи, напевая приятную мелодию, мысленно представляя себе живописный пейзаж[58]. А есть счастливчики, расширяющие во время такой душевной медитации список изящного. Они, например, отслеживают про себя побайтный обмен данных на шине компьютера, составляют в голове программу для него или доказывают математическую теорему: Как мысли черные к тебе придут, откупори шампанского бутылку иль пере... реши задачу Коши. Ответ же ищется и численно, и аналитически, и... интуитивно. Присниться может не только таблица химических элементов (и не только Менделееву), но и... неведомое семейство кривых или небывалая структура данных.
По мнению таких «чудаков» (а на них держится настоящая математика), взятие интеграла на ЭВМ равносильно... сочинению стихов на компьютере. И в плане кощунственности самой мысли, и в плане практической, а тем более общеобразовательной (эстетической) пользы. Мы недаром подчеркнули триединство процесса решения задачи. Численные и даже аналитические методы можно отдать на откуп машине. Но интуицию...
[1] Тут правильнее говорить о компьютерной математике аналитических преобразований, но у нас уже прижилась калька с английского термина Symbolic Mathematic ¾ символьная математика.
[2] В пятой версии Mathcad порядок производной не мог быть переменной величиной. В шестом Mathcad’е этот недостаток был исправлен.
[3] Приставка Pro (professional) в названии пакета свидетельствует о том, что в него включены и средства символьной математики.
[4] Это деление не совсем логично: Во-первых, есть еще команды символьных преобразований, требующие указания переменной, к которым они относятся, ¾ преобразование Лапласа, например. Во-вторых, команды Expand (разложить по степеням) и Factor (представить в виде произведения) в их операторных аналогах (см. раздел 7.2) также могут требовать указания переменной, относительно которой данное действие производится.
[5] О том, что проще — x2
или x×x, можно еще спорить.
[6] У нас еще говорят «с плавающей десятичной запятой», учитывая тот факт, что на бумаге мы по-прежнему отделяем целую часть от дробной запятой, а не точкой. Из-за этого возможны конфликты при передаче данных из среды Mathcad в среду Excel (см. приложение 9), где нередко при настройке в качестве разделителя в вещественном числе выбирается запятая, а не точка.
[7] Вот полный список таких функций и констант: arcsec, arccsc, arccot, arcsech, arcscsh, arccoth, g, Catalan's constant, Chi(x), Ci(x), csgn(x), dilog(x), Dirac(x), Ei(x), erf(z), FresnelC(x), FresnelS(x), GAMMA(z), hypergeom(n1, n2..., d1, d2..., z), LegendreE(x,k), LegendreEc(k), LegendreEc1(k), LegendreF(x,k), LegendreKc(k), LegendreKc1(k), LegendrePi(x,n,k), LegendrePic(n,k), LegendrePic1(n,k), Psi(n,x), Psi(x), Shi(x), Si(x), signum(x), W(x), W(n,x) и Zeta(s). Если читатель с ними столкнется, работая в среде Mathcad, то ему нужно будет обратиться к help’у.
[8] В шестой и седьмой версиях Mathcad при включении в работу символьного процессора вместо привычного курсора мыши (стрелка) появляется докторская четырехуголка. В четвертой и пятой версиях курсор превращался в кленовый лист: maple по-английски «клен» - фирма Waterloo Maple находится в Канаде.
[9] В сети Internet по адресу ftp.wustl.edu/doc/misc/pi можно найти число ? с 1 500 000 знаками.
[10] Напоминаем, что в среде Mathcad 8 Pro недопустимы буквы кириллицы в именах переменных при символьных преобразованиях.
[11] Не к ночи будет упомянут, хотя «крестная мама» диамата — классическая философия Гегеля вдохновила автора на работу над книгой под условным названием «Философия программирования».
[12] В восьмой версии Mathcad невязка уже не показывается, так как от нее мало было толку
[13] Это не команда, а переключатель режимов символьных преобразований.
[14] Ее не любят только две категории людей: ущербные люди, которые никого и ничего любить не могут, и люди, с математикой незнакомые. Но любовь автора к математике, увы, не совсем взаимна. Автор в свое время не получил должного математического образования. Отсюда некоторые, мягко говоря, «нестыковки», которые настоящий математик обязательно увидит в книге. Пример: взятие производной и дифференцирование — это далеко не одно и то же.
[15] ОТЦ — имеются в виду электрические, а не пролетарские цепи. У дисциплины « Основы теории пролетарских цепей» другое название — «Политэкономия капитализма». У нас в МЭИ ОТЦ блестяще читал профессор Карл Круг, о котором рассказывали такую страшилку. Сдает студент экзамен по ОТЦ, а Круг его прерывает и говорит: «Да вы, батенька, не знаете закона Ома. Что у вас по физике?» Круг перелистывал страницы зачетки, видел тройку по физике, зачеркивал ее и говорил обалдевшему студенту: «Сначала выучите и сдайте физику, а уж потом приступайте к моей дисциплине».
[16] Случай, когда без команд символьных преобразований не обойтись, ниже на рис. 7.10.
[17] В настоящее время компьютерными символьными преобразованиями проверяются выкладки великих математиков. Ни одной ошибки не нашли пока только у «короля» математиков — Гаусса (см. раздел 7.3). Компьютерной математикой стоит контролировать свои собственные аналитические выкладки.
[18] Новое — это хорошо забытое старое: см. рис.1.4 в этюде 1.
[19] Константа интегрирования, как мы уже отметили ранее, опускается (полагается равной нулю).
[20] В среде Mathcad PLUS 6.0, который у нас до сих пор очень популярен по двум причинам — наличие русифицированной версии и возможность работы под управлением Windows 3.1 на не очень мощных компьютерах («тройки» и «четверки»), направление символьных преобразований оператором g ® задавалось семью ключевыми словами: (factor, expand, series, simplify, complex, float и assume), которые писались до данного оператора. Это было очень неудобно. Во-первых, в ключевом слове можно было сделать ошибку — написать, например, вместо слова Simplify слово Simplifi. В этой ситуации пакет Mathcad ошибку не фиксирует, но и выражение не упрощает.
[21] Команда Simplify меню Symbolic богаче своего тезки-оператора: командой Simplify можно упростить только часть выражения, отмеченную курсором (см. выше).
[22] Единица не входит в множество «простые числа».
[23] Подпись (электронная или обычная) — это гарантия того, что письмо послано именно тем, чей обратный адрес стоит на конверте. Более того, если нужно будет доказать третьей стороне (судье, например) подлинность сообщения, то это можно сделать так, что ни корреспондент, ни адресат не будут это оспаривать.
[24] Такая идиома встречается во многих книгах. При этом как-то упускается из виду, что через пять-десять лет может быть создан компьютер (транспьютер!), который с данной задачей справится уже за приемлемое время. Для такой работы можно объединить разные компьютеры в сеть. Кроме того, «миллион лет» – это не число, а элемент нечеткого множества «очень долго».
[25] Рекорд (самое большое простое число Мерсенна) на 1 июня 1999 – 26772593-1.
[26] Суперкомпьютер, конечно, по меркам 1982 года.
[27] Большая теорема Ферма утверждает, что an+bn=cn только при n2 (32+42=52).
[28] Это делают, конечно, не в среде Mathcad, а с помощью специальных программ, способных возводить в огромную степень огромные числа. Кстати говоря, функция Ferma с выбранными на рис. 7.11 аргументами работает в среде Mathcad 7, но не работает в среде Mathcad 8. Это к нашему тезису о «капризной бабе» под названием символьная математика.
[29] Мартин Гарднер долгое время редактировал рубрику «Занимательная математика» в этом журнале, материалы которой легли в основу его знаменитых книг.
[30] Числа перемножены не оператором n1×n2=, а командой Вычислить символьной математики.
[31] Название приза зашифровано способом, который использовал еще Юлий Цезарь.
[32] В продаже есть и калькуляторы с символьным процессором (например TI-97).
[33] Если n не указано, то возвращается 20 знаков по умолчанию.
[34] Третье отличие команд символьных преобразований от аналогичных операторов: команда float может вывести до 4000 знаков, оператор — до 250.
[35] В шестой версии Mathcad в ходу был термин «SmartMath» — сообразительная математика.
[36] Символ интеграла — это растянутая буква s, первая в слове summa.
[37] Напоминаем, что в среде Mathcad 8 возможен выбор способа численного интегрирования.
[38] У выражения может быть три режима: а) выражение может быть подсвечено (цвет фона отличается от основного — таким образом можно на данное выражение обратить внимание пользователя); б) выражение может быть выключено из расчетов (стать простым комментарием) и в) выражение может быть оптимизировано.
[39] В шестой версии Mathcad командой на локальную оптимизацию служило ключевое слово optimize, поставленное перед выражением. Ключевое слово literally отменяло оптимизацию следующего за ним выражения при включенном режиме глобальной оптимизации. В среде Mathcad 8 также можно включить режим оптимизации всех выражений, а затем через флажок Enable Optimization отключить оптимизацию у некоторых формул.
[40] Намек на то, что самые лучшие математики — это советские евреи.
[41] Становится меньше не только математиков, готовящихся к занятиям, но и просто хороших математиков. Печальная шутка: «Что такое американский университет? Это место, где бывший советский (вспомним красную шестиугольную звездочку на рис. 7.14) на ломаном английском преподает математику китайцам».
[42] Есть горе от ума, а есть горе от компьютеров и, вообще, от горе всяческих плодов цивилизации.
[43] Пример спортивного тренажера казался автору вполне удачным до тех пор, пока он не узнал, что современные тренажеры (тот же Ketler, мелькающий в рекламе по TV) на самом деле оборудованы силовыми приводами, помогающими человеку или тормозящими рычаги в нужный момент. Этим настоящие тренажеры отличаются от простого троса, перекинутого через блок, с грузом на конце.
[44] Этот документ работает в среде Mathcad 7 и не работает в среде Mathcad 8. Ошибки программирования исправлены по принципу «Есть оператор — есть проблема, нет оператора — нет проблемы».
[45] Разработка фирмы Waterloo Maple, Inc., 450 Phillip Street, Waterloo, ON, Canada, N2L 5J2, тел.: 519-747-23, факс: 519-747-5284, http://www.maplesoft.com. Символ V в названии пакета – это латинская буква V (Victory – победа). Далее в тексте мы ее будем опускать – в новейшей версии этого пакета она также опущена – Maple 6. В конце приложения 1 указано, что в Mathcad встроен MKM (MathSoft Kernel Maple), разработанный фирмой Waterloo Maple, Inc.
[46] С другой стороны, «настоящие» научные дисциплины не боятся прилагательного «занимательный»: занимательная математика, занимательная физика и т.д. Но! «Занимательный научный коммунизм» — как вам это понравится?.. Ладно, не будем пинать издыхающего льва — «Занимательная астрология».
[47] Развитие пакета Mathcad для компьютеров Apple Macintosh остановилось на пятой версии, а для DOS — на версии 2.51.
[48] Это был своеобразный протест против господства числа в Computer Science.
[49] Автор давным-давно написал статью о принципах расцвечивания программ и послал ее в журнал «Микропроцессорные средства и системы» (в то время единственный, где публиковались статьи по персональным компьютерам). Статья попала на рецензию… к дальтонику.
[50] Этот принцип применительно к работе на компьютере можно переиначить так: не спеши изучать языки программирования — очень вероятно, что этого не понадобится: программные среды Mathcad и Maple позволяют решать довольно сложные задачи без традиционного кодирования алгоритмов.
[51] В среде языка BASIC ключевое слово print можно заменить знаком вопроса, а в среде Maple совсем опустить — сравните рис. 7.21 и 7.22.
[52] Еще раз напомним, что вычислительная математика Mathcad допускает буквы кириллицы в именах переменных и функций. В символьной математике и Mathcad и Maple этого делать нельзя. Поэтому на рис. 7.24 мы работаем не с переменной Пр, а с переменной Pr.
[53] Приводим цены во французских франках (5 франков » 1 доллар США) из рекламы, помещенной в журнале La Recherche (№ 10’96): Maple V Release 4 — 6450 (3490 — для учебных заведений), Mathcad 6.0 PLUS — 3490, Mathcad 6.0 — 1490. Но самый дорогой математический пакет — это, конечно, Mathematica 3.0 — 8950 (6965). В Москве у фирмы SoftLine (тел. 232-00-23) учебные заведения могут купить Maple за 600 долл., а Mathcad (русскую версию) — за 420 долл. — см. рекламу в конце книги.
[54] Многие молодые читатели их не застали, поэтому автор излагает здесь азы кибернетики.
[55] Главная причина смерти АВМ в том, что на цифровой машине можно смоделировать аналоговую, а на аналоговой цифровую — нет.
[56] Или гибридностью, если вспомнить название раздела книги.
[57] Это возможно только в седьмой версии Mathcad. В более ранних версиях команды символьных преобразований из меню Symbolic с вложенными пользовательскими функциями не работали.
[58] Умный человек никогда не будет скучать с самим собой.
Семь замечаний
1. Автор, естественно, постарался исправить ошибки и опечатки первого издания. В этом ему помогли знакомые и незнакомые коллеги, которым автор безмерно благодарен.
2. В качестве официального бета-тестера автор участвовал в испытаниях бета-версии седьмого Mathcad. Это позволило ему, во-первых, заглянуть в «кухню» фирмы MathSoft, а во-вторых, заранее (до выхода программного продукта) основательно «обыграть» новинки Mathcad 7 Pro.
3. Не оставлена без внимания и предыдущая версия Mathcad — Mathcad PLUS 6.0. Дело в том, что седьмой Mathcad предъявляет высокие требования к компьютеру (Windows 95, 16 Мбайт ОЗУ и др.). Книга адресована студентам и инженерам, для многих из которых по техническим причинам даже Windows 3.x недоступен. Есть, кстати, и DOS-версия Mathcad, работающая и на IBM без винчестера, и с 1 Мбайт оперативной памяти. Почти все задачи книги (кроме тех, которые помещены в этюдах 6 и 7) работают и в среде Mathcad под управлением DOS.
4. Автор активно включился в процесс формирования «мирового решателя» задач с использованием Mathcad: все программы книги размещены на серверах.
5. Книга имеет гриф учебного пособия, поэтому при ее переработке были учтены те трудности, с которыми студенты сталкивались при освоении Mathcad с помощью данной книги.
6. Одновременно с написанием книги автор создавал обучающий мультимедийный курс (CD-ROM) по программе Mathcad в фирме «МультиМедиа Технологии» (111116 Москва, ул. Энергетическая, 8/2, тел. (095) 362-74-86, e-mail mmt@glas.apc.org). Автор надеется, что книга и курс выйдут одновременно и дополнят друг друга[1]. На CD-ROM предполагается разместить русскую легальную версию Mathcad PLUS 6.0[2]. Так что его пользователь сбросит с себя груз проблем, описанных в разделе 6.10 данной книги.
7. Автор будет благодарен за замечания и пожелания по книге, которые просит направлять по обычной (111250 Россия, Москва, Красноказарменная, 14, МЭИ, ТВТ) или по электронной (ochkov@twt.mpei.ac.ru) почте. Сами же файлы с задачами книги хранятся по адресу ftp:\\twt.mpei.ac.ru\book.mcd.
И последнее замечание. Люди, много работавшие с языком fortran, знают, что это не просто язык кодирования алгоритмов, а целый мир со своими судьбами, легендами, удачами и неудачами... Среду Mathcad можно и нужно рассматривать не только как среду программирования, но и как некую сферу культуры, составляющую пласт мировой культуры. Эту идею автор постарался пронести сквозь книгу, которую можно и нужно рассматривать, только как учебное пособие по популярной программной среде, но и как сборник рассказов об околокомпьютерной жизни.
Следует читать
Формируя пользовательскую интерполирующую функцию, необходимо
Формируя пользовательскую интерполирующую функцию, необходимо сразу освободиться от размерностей аргументов, приведя их к безразмерной величине относительно данных в боковике (у нас это температура) и шапке (давление) таблицы узловых (опорных) точек. Размерность функции, соответствующая данным в таблице, приписывается к возвращаемой величине в конце формируемой функции.
Все это позволяет иметь в качестве аргументов функции величины с любой допустимой размерностью температуры и давления и получать удельную энтальпию также с различной размерностью (см. рис. 4.10).
Интерполяция, как правило, ведется в оговоренном диапазоне значений аргументов. Поэтому будет целесообразно вставить в функцию пользовательские сообщения об ошибке – о выходе за пределы разумных значений аргументов[13]. Для этого предназначена встроенная в Mathcad функция error(“Сообщение об ошибке”), прерывающая выполнение вычислительной процедуры и своим комментарием призывающая пользователя исправить оплошность. Если пользователь «подсунет» функции hss(T, P), к примеру, не температуру и давление, а массу и длину, то заработает уже встроенное сообщение об ошибке “The units in the expression do not match” (Единицы в выражении не соответствуют правилам – см. рис. 4.11):
Методика двухмерной сплайн-интерполяции, реализованная в Mathcad, требует, чтобы табличные значения двух аргументов хранилась в матрице с двумя столбцами, а табличные значения функции – в квадратной матрице. Для лучшего обзора и редактирования табличные данные можно временно объединить в одной квадратной матрице (у нас ее имя M, а размер (порядок) 19 на 19 – см. рис. 4.10), где первый столбец без первого элемента – это табличные значения температуры (первый аргумент формируемой функции), а первая строка без первого элемента – табличные значения давления (второй аргумент). Последующие манипуляции функцией submatrix раскладывают все «по полкам» – матрица TP с двумя столбцами и с 18 строками хранит табличные значения аргументов, а квадратная матрица H с порядком 18 – табличные значения удельной энтальпии. Так можно добиться компромисса между требованиями Mathcad и требованиями наглядного размещения данных.
Для лучшего обзора исходных данных и для разделения их на функциональные группы в исходной матрице можно записывать числовые константы (элементы матрицы) с различным видом и размером шрифта – см. рис. 4.10 (непронумерованный совет).
Никогда не стоит опираться на конкретное значение системной переменной ORIGIN (номер первой строки и первого столбца матриц) и на конкретный размер матриц. В функции hss(T, P) записан оператор «вырезания куска» из матрицы M – вектора табличных значений температур:
TP<ORIGIN>¬submatrix(M, ORIGIN + 1, rows(M) - 1, ORIGIN + 1, cols(M) - 1),
а не
TP<0>¬submatrix(M, 1, 18, 1, 18)
Два эти выражения эквивалентны только при ORIGIN=0 (умолчание Mathcad) и при порядке матрицы M, равном 19. При других значениях переменной ORIGIN и при других размерах матрицы M второе выражение при вызове функции hss даст сбой.
Очень часто табличные данные, отображающие значения какой-либо физической величины (удельной энтальпии водяного пара, как в нашем случае), не укладываются в отведенные им в среде Mathcad сугубо квадратные рамки. На место отсутствующих данных (левый нижний и правый верхний угол нашей квадратной матрицы) можно записать что-то, резко отличающееся от «настоящих» данных. У нас это минус единица. Возврат значения функции нужно предварить оператором error (см. предпоследнюю строку на рис. 4.10), прерывающим расчет, если возвращаемое значение «не лезет ни в какие ворота» в смысле порядка величины. В нашем случае с функцией hss(T, P) значение энтальпии не может быть меньше, чем 1930.8 кДж/кг – наименьшее «разумное» значения матрицы энтальпий. Если так получилось, то это означает, что при интерполяции «захвачена» минус единица и решение неверно.
При подготовке Mathcad-документа к публикации стоит переместить копию экрана дисплея (клавиша PrtSc) в среду какого-либо графического редактора (Paintbrush, например) и там его доработать. Основные направления доработки, которыми автор воспользовался, готовя иллюстрации к этой книге:
вертикальная линия, отмечающая начало и конец процедуры формирования функции пользователя hss(T, P) на рис. 4.10, изогнута, что позволило сделать листинг более компактным;
для этой же цели были убраны столбцы, хранящие энтальпию пара при 8, 10, 12, 15, 20 и 22 МПа;
в среде графического редактора в Mathcad-документ можно внести то, что в среде Mathcad не внесешь, например, вертикальный комментарий на месте стертых столбцов и другие пометки – см. рисунки книги;
копируя экран дисплея, можно захватить информацию, которая при простой распечатке Mathcad-документа (команда Print в меню File) пропадает. Это, во-первых, встроенные и пользовательские сообщения об ошибках – см. рис. 4.11. Можно из разных копий экрана дисплея, фиксирующих различные моменты диалога пользователя с компьютером, собрать один: на рис. 4.11 выведены все три сообщения об ошибках, хотя на экране дисплея одновременно можно видеть лишь одну – ту, которая выпадает из «покрасневшей от ошибки» функции, когда пользователь наводит на нее курсор мыши.
На рис. 4.12 проиллюстрирован вызов функции hss(T, P) при различных значениях и различных размерностях аргументов. Размерность возвращаемой функцией удельной энтальпии пользователь также вправе менять.
Translation into English by R.Girvin
This problem of a label – or more correctly, problem of disposing with a label -– we'll look at in solving an ancient English puzzle about fishermen and fish:
"Three fishermen lay down to sleep, not having counted or divided their catch. In the night, one of them woke up, and (not quite trusting the others) decided to divide the pile of fish and take his share. But the number of fish wasn't visible by three. However, he found he could throw one fish away, then take exactly a third. This he did (noting, in the true spirit of fairness, that an even number of fish was left for his comrades) and went back to sleep. Later, the second and third fishermen woke in turn, and each went through the same process. The question is, what is the minimum number of fish in the catch that fulfils these conditions?"
The reader might like first to try to solve this task by hand; but we'll involve the computer in this for two reasons. Firstly, it lets us consider some ways to structuralize programs in the Mathcad environment: methods of clearing programs of labels, and 'squeezing' them into the rigorous framework of structural design. Secondly, we'll show that the Fishermen's Problem has, until now, been solved incorrectly...
A pirate's open letter to computer publications
(Translation into English by R.Girvin)
1. A philosophical-religious aspect of the problem
2. A cultural aspect of the problem
3. A police aspect of the problem
4. A moral aspect of the problem
On opening any issue of any computer publication, one can stumble upon articles concerning the problem of illegal copying and program distribution. This letter broaches this subject, but in a slightly different context. It makes no attempt to condemn or justify piracy. The author merely tries to examine this problem from unusual angles: philosophical, religious, cultural, police, moral ... and even sexual.
Три дивертисмента
1. Дивертисмент политический.
Наши политики, обсуждая статус Чечни (Страны Басков, Корсики и др.) загоняют себя в угол. Мол, независимость – это как беременность: она либо есть, либо ее нет. Нельзя быть чуть-чуть беременной, нельзя быть чуть-чуть независимой и т.д. и т.п.
Это противоречие можно разрешить с помощью теории нечетких множеств. Рассказ о ее основах обычно начинают с парадокса кучи зерна. Сто зерен – это куча или нет? Конечно, нет, – это скорее горсть
зерна. А если к этой горсти прибавить еще одно зерно, станет ли она кучей? Опять нет. А если еще зерно и еще зерно. Рано или поздно мы получим кучу. Люди пытались с позиций классической математики определить точное число зерен, разграничивающее горсть и кучу, но ничего путного из этого не получалось. Примерно так сейчас политики пытаются найти количество признаков (полномочий), отделяющих независимое государство от субъекта федерации. Все бы ничего, да кровь льется.
Дело в том, что понятие «независимое государство» традиционно (исторически) рассматривается как элемент четкого множества. Дескать, государственное образование может либо принадлежать, либо не принадлежать к этому множеству.
Но все намного сложнее и намного проще. Понятие горсть и куча – это нечеткие множества. Сто зерен – это одновременно и горсть и куча. При этом значение функции принадлежности ста зерен к множеству горсть равна почти единице, а к множеству куча – почти нулю. Если к этой сотне добавить зернышко, то первое значение (близкое к единице) чуть-чуть уменьшится, а второе (близкое к нулю) – чуть-чуть увеличится. Опять повторяем – природа не терпит острых углов и черно-белых оценок.
Проблема кучи зерна решается с позиции теории нечетких множеств так: насыпаются разные количества зерен, а люди (эксперты; лица, принимающие решения) дают такие оценки: «это горсть (0)», «это скорее горсть, чем куча (0.33)», «это скорее куча, чем горсть (0.67)», это и не горсть и не куча, а что-то среднее (0.5), «это куча (1)» и т.д. (так сейчас, к примеру, проводят опрос общественного мнения). После этого строится функция принадлежности (см. главку в этюде 6) к нечеткому множеству «куча зерна». График этой функции – плавная и пушистая кривая, поднимающаяся от нуля (мало зерен) к единице (много зерен) без каких-либо скачков. Функция принадлежности к множеству «горсть зерна» имеет «горбатый» график: нули по краям (идем от отдельных зерен к куче) и единица посредине (горсть зерна).
Проблема Чечни – это проблема не только России, но и всего мирового сообщества в том плане, что в уставе ООН заложены два взаимоисключающих принципа – принцип нерушимости границ и право нации на самоопределение (на независимость). Решить эту проблему можно, приняв во внимание, что понятия «нация» и «независимое государство» – это также нечеткие множества. Государственное образование (область, район, республика) может быть и чуть-чуть независимым и совсем независимым. Читатель может сам при желании составить такую таблицу: в первой колонке написать названия стран (включая субъекты Российской Федерации), а во второй – значение функции принадлежности этих стран к множеству «независимое государство». Германия независимое государство или нет!? Вроде бы да, но многие ее суверенные полномочия ограничены членством в НАТО, в Европейском Союзе, в Общем рынке и т.д. Такой важный атрибут независимости, как национальная валюта, и та скоро у Германии пропадет (евро!). Немецкий язык все больше становится неким местным диалектом – все серьезные научные конференции проводятся на английском языке. Так что «независимости» у этой страны сейчас намного меньше, чем у той же Чечни. Говоря языком теории нечетких множеств, можно сказать, что значение функции принадлежности к множеству «независимые государства» у Германии ниже, чем у Чечни. То, что в Бонне много посольств иностранных государств, а в Грозном пока ни одного, ни о чем не говорит. Представим себе, что завтра все страны порвут с Германией дипломатические отношения. От этого статус Германии как независимого государства только повысится. На нашей планете самые независимые – это самые одиозные государства: «алкоголики» (поставщики наркотиков), «тунеядцы» (страны, живущие за счет помощи мирового сообщества), «хулиганы» (Ливия, Ирак, Северная Корея – маленькие «хулиганы», Россия, США, Китай – взрослые «хулиганы»). «Алкоголиков» и «тунеядцев» называть не будем – где здесь вина, а где беда этих стран? «Казнить нельзя помиловать!»
Итак, будем считать, это все субъекты Российской Федерации – независимые государства, но значения функции принадлежности у них к этому нечеткому множеству разные: у Тверской области одно, у Татарстана – другое, а у Чечни третье, самое высокое. В процессе государственного строительства эти числа могут меняться плавно (реформы) либо скачками (революции, войны, но лучше – референдумы), но никогда они не упадут до нуля и не поднимутся до единицы.
2. Дивертисмент политико-компьютерный.
Теории нечетких множеств и нечеткой логики можно приложить и к проблеме компьютерного пиратства. Закон делит всех людей на два четких множества: «множество легальных пользователей программ» и «множество нелегальных пользователей (пиратов)». В реальной жизни все намного сложней: нечетких множеств людей, причастных к компьютерам, великое множество (извините за тавтологию). Есть множество торгующих на «Горбушке» «черными» дисками и есть множество
тех, кто принципиально работает только с легальными копиями и никогда не подаст руки согрешившим – нарушившим какое-либо лицензионное соглашение. Можно осью «грешник-праведник» построить горбатые статистические кривые, описывающие состояние компьютерного рынка в конкретной стране. Где находится максимум этой кривой, куда и с какой скоростью он перемещается во времени?
3. Дивертисмент компьютерный.
Даниил Хармс[33]
подметил, что память – это очень странная штука: иногда запомнишь одно, а вспомнишь потом совсем другое. А бывает и так, что запомнишь настолько крепко, что потом ни за что не вспомнишь.
Основное отличие памяти человека от «памяти» компьютера в том, что человек разную
информацию запоминает по-разному. Одно дело запомнить телефон случайного знакомого, а другое дело такую информацию: «Еще раз сунешь сюда нос – голову оторву!»
Элементарные ячейки памяти цифрового компьютера хранят либо нули, либо единицы, не делая никаких различий по важности информации. «Бит» информации в мозге человека – это нейронная связь различной «толщины», меняющейся, условно говоря, от нуля до единицы. Может быть, стоит заряжать конденсаторы компьютера не ступенькой, а плавно…
Семь дивертисментов к трем дивертисментам.
А вот еще примеры того, что в жизни нет чистых нулей и единиц – нет четких и однозначных ответов на, казалось бы, самые простые вопросы.
1. Считается, что костры в лесу увеличивают опасность пожаров. Но! Туристы, собирающие для костров хворост и сухостой, культурно
сжигают горючий материал, готовый вспыхнуть от удара молнии или от неосторожно брошенной сигареты. Так что костры в лесу не губят (не только губят),а защищают лес от пожара.
2. Российские политики из кожи лезут вон, добиваясь, чтобы транзитные нефтепроводы из района Каспия проходили исключительно через российскую территорию. Считается, что обходные пути перекачки нефти лишат Россию огромных доходов и политического влияния. Но! Влиять на кого-то шантажом перекрытия задвижки крайне аморально. Экономический же эффект транзита нефти может быть подсчитан только после оценки ущерба, наносимого России разрывами
трубопроводов и другими авариями. Мы должны всеми правдами и неправдами добиваться прокладки трубопроводов минуя российскую территорию. Новые трубопроводы нужно прокладывать лишь после того, когда уровень эксплуатации существующих трубопроводов станет приемлемой. Это касается и газопроводов – вспомним, как под Уфой в огне сгорели два пассажирских поезда. В нормальной стране после такой катастрофы любой Газпром разорился бы, выплачивая страховки. А у нас ничего…
3. В настоящее время в мире ведется кампания по тотальному запрещению противопехотных мин. Символ этой кампании – безногий ребенок на костылях, подорвавшийся на мине, оставшейся от давнего конфликта. Но! Если бы в свое время конфликтующие стороны (например, представители народностей тутси и хуту в Бурунди) не отделили бы друг от друга минными полями, проходы в которых контролировали нейтральные силы (войска ООН, например), то жертв, в том числе и среди женщин, стариков и детей, могло бы быть намного больше. Плохи не противопехотные мины, а люди, забывающие или не умеющие ликвидировать их после окончания конфликта.
4. Расхожий лозунг ура-патриотов: «Если народ не хочет кормить свою армию, то он будет кормить чужую». Мы вскармливали Советскую армию, которая стреляла в мирных людей в Новочеркасске, с позором выходила из Венгрии, Чехословакии, Германии, Афганистана, Чечни... Красную Армию немецкие войска в 1941 году разбили за пару месяцев, а Победу добывал уж сам народ-кормилец (с помощью Мороза-воеводы): инженеры, учителя и прочий рабочий люд на целые четыре года оставили свой мирный труд и взялись за оружие. Про армию трудно судить, но вот отечественную милицию, а тем более ГАИ (ГИБДД) стоило бы поменять на импортную, некоррумпированную (на немецкую, например). Эффективнее и, что интересно, дешевле бы вышло. Армию же вообще не стоит содержать – ни свою, ни чужую. Ракетно-ядерные силы сдерживания – это по своей сути никакая не армия, а научно-техническая отрасль, работникам которой зачем-то погоны прицепили.
5. Оружие у населения у нас считают одним из главных факторов роста преступности. Но! Демократия вместе с порядком (Законом) воцарилась в Западной Европе лишь после того, как крестьяне взяли в руки оружие и стали защищать себя от средневекового рэкета – от произвола синьора. Сможет ли современная «аристократия» («братки[34]», «крыша») обкладывать поборами современных «крестьян» (предпринимателей), зная, что вместо денег можно получить пулю в лоб – и все будет законно. В стране не было бы никакого 37 года, если бы хозяева «черных воронков» (НКВДАПО) боялись хотя бы вооруженного сопротивления арестовываемых.
6. Сейчас ни у кого не поворачивается язык сказать ничего, кроме слов осуждения, в адрес террористов. При этом специально ставят на одну доску людей, захватывающих невинных жертв, и людей, вынужденных браться за оружие для решения своих политических и иных проблем (см. выше). С первыми все более-менее ясно, их нужно рассматривать как некое стихийное бедствие, от которого никто не застрахован. Нужно только стараться под него не попадать, а если попал, то правильно себя вести. Со вторым же типом «террористов» не все так просто. К ним можно отнести принцип «на то щука в море, чтобы карась не дремал». Говорят, что можно устранить любого политического деятеля – все дело в средствах, которые на это можно ассигновать (инвестировать). Того или иного лидера не устраняют не только потому, что у него сильная охрана, но и потому, что это никому пока не нужно. Или нет средств на это. Политический деятель ведет себя прилично, боясь в том числе и пули своих оппонентов (своего народа).
7. Целостность России наши политики возводят в ранг некоего идола, которому нужно приносить огромные жертвы. Но! Все дело в том, что настоящие люди чувствуют себя не только россиянами, но и европейцами, гражданами Мира. Национализм, как верно подмечено, – это последнее прибежище негодяев. Многие русские люди отделились бы от Москвы и присоединились бы, например, к Страсбургу, но не имеют на то сил, а, главное, повода. Уезжать из этой страны? Нет, спасибо! Пусть лучше уезжают те, от кого нам хочется отделиться…
Мысли, конечно, очень спорные и где-то даже извращенные, но… еще раз взглянем на название этюда…
Задачи книги
1. Задача о купце и сукне (решение системы алгебраических уравнений – рис. 1.1, рис. 1.4-1.8, 1.14 и 7.7)
2. Графическое решение системы алгебраических уравнений – рис. 1.8
3. Задача о летящих гусях (поиск корня уравнения – стр. 40)
4. Задача о покупке иномарки (поиск корня уравнения – стр. 40)
5. Поиск корней полинома – рис. 1.11
6. Пересчет показаний манометра – стр. 46 и 47
7. Рост Эркюля Пуаро – стр. 49
8. Длина удава, Попугая, Мартышки и Слона – стр. 49
9. Равновесие балки (решение системы алгебраических уравнений с учетом размерности – рис. 1.15, 7.8 и 7.25)
10. Равновесие балки (решение системы линейных алгебраических уравнений – рис. 1.16)
11. Построение графиков:
– декартового – рис. 1.17
– параметрического – рис. 1.18
–полярного – рис. 1.19
– поверхности – рис. 1.21
– векторного поля – рис. 1.22
– карты линий уровня – рис. 1.23
– трехмерного точечного – рис. 1.24
– трехмерного столбчатого – рис. 1.25
12. Задача о пожарном ведре (одномерная оптимизация – рис. 2.2, 3.9, 6.41-6.45, 7.27 и 7.31)
13. Задача о двух пожарных ведрах (одномерная оптимизация – рис. 2.3, 3.9, 6.28, 7.28 и 7.31)
14. Задача о коробке (одномерная оптимизация – рис. 2.4)
15. Задача о коробках (одномерная оптимизация – рис. 2.5 и 2.6)
16. Задача о коробках (двух-, трех-, и многомерная оптимизация – рис. 2.7, 7.12 и 7.32)
17. Задача о трех пожарных ведрах (двухмерная оптимизация – рис. 2.8 и 7.27)
18. Задача об оптимальном плане выпуска стульев (задача линейного программирования – рис. 2.9, 3.10 и 7.28)
19. Оптимизация перевозок (транспортная задача – рис. 2.10 и 3.13)
20. Поиск корней алгебраического уравнения – рис. 3.1, 6.1, 6.17-6.21 и 6.54
21. Поиск минимума двухмерной экспоненциальной функции – рис. 3.3
22. Поиск минимума двухмерной экспоненциальной функции Розенброка – рис. 3.4, 7.8 и 7.28
23. Поиск минимума двухмерной экспоненциальной функции Пауэла – рис. 3.5
24. Интегрирование методом Монте-Карло (рисование на компьютере – рис. 3.6)
25. Расчет объема конуса (ваяние на компьютере – рис. 3.7 и 3.8)
26. Задача о краске (целочисленное линейное программирование – рис. 3.11, 6.31 и 6.32)
27. Поиск метода для ларька (целочисленная оптимизация – рис. 3.12 и 6.8)
28. Выключатель на дачу – стр. 140
29. Машинка для голосования простым большинством – стр. 140
30. Машинка для голосования в СБ ООН – стр. 141
31. Сортировка вектора – рис. 4.1
32. Линейная аппроксимация – рис. 4.2
33. Аппроксимация полиномом – рис. 4.4
34. Нелинейная аппроксимация – рис. 4.5 и 4.6
35. Линейная интерполяция – рис. 4.7
36. Интерполяция сплайном – рис. 7.8
37. Определение удельной энтальпии перегретого водяного пара как функции температуры и давления – рис. 4.10-4.12
38. Определение удельного объема воды как функции температуры – рис. 4.13
39. Экстраполяция – рис. 4.14
40. Сглаживание табличных зависимостей – рис. 4.15
41. Оценка качеств менеджера – рис. 4.16 и 4.17
42. Моделирование развития эпидемии – рис. 5.1-5.5 и 7.24
43. Моделирование развития финансовой пирамиды – рис. 5.6 и 5.7
44. Решение обыкновенных дифференциальных уравнений – рис. 6.3, 6.5, 7.5 и 7.23
45. Расчет ставки налога – рис. 6.4
46. Решение численной головоломки – рис. 6.6
47. Задача об изобретателе шахмат – рис. 6.7
48. Пасьянс «Турецкий платок» – рис. 6.9
49. Поиск факториала – рис. 6.10
50. Числа Фибоначчи – рис. 6.11, 6.12 и 7.30
51. Числа Аккермана – рис. 6.13
52. Головоломка «Ханойские башни» – рис. 6.14
53. Параметры треугольника – рис. 6.15
54. Задача о рыбаках и рыбке – рис. 6.23 и 6.24
55. Графическое решение неравенства – рис. 6.25
56. Поиск минимума методом золотого сечения – рис. 6.26 и 6.53
57. Поиск минимума методом «Два шага» – рис. 6.27
58. След оптимизации – рис. 6.29 и 6.30
59. Задача о плане выпуска компьютеров – рис. 6.33-6.35
60. Трехсторонняя дуэль – рис. 6.36-6.40
61. Римские и арабские числа – рис. 6.46 и 6.47
62. Кпд термодинамического цикла – рис. 6.49-6.52
63. Поиск минимума половинным делением – рис. 6.55
64. Поиск простых чисел – рис. 7.11
Предметный указатель
| Axum | 68 |
| DDE | |
| Drag-and-drop | |
| EXCEL | |
| KISS-принцип | |
| Lotus | |
| MAPLE | |
| Mathematica | |
| MatLab | |
| OLE | |
| QuattroPro | |
| Remake | |
| Альтернатива | |
| Анализ регрессионный | |
| Анимация | |
| Аргумент функции | |
| АСНИ | |
| Буфер обмена | |
| Вектор | |
| Ветвление множественное | |
| Выражение оптимизирующее | |
| Генератор псевдослучайных чисел | |
| Генератор случайных чисел | |
| Геометрия неевклидова | |
| Гражданская война | |
| График векторного поля | |
| График гистограммы | |
| График декартов | |
| График линий уровня | |
| График параметрический | |
| График поверхности | |
| График полярный | |
| График рассеяния | |
| График сечения поверхности | |
| День «икс» | |
| Диаграмма структурная | |
| Задача Коши | |
| Задача маленького Гаусса | |
| Запись переменных | |
| Индекс текстовый | |
| Индекс числовой | |
| Интерполяция | |
| Инфляция | |
| Камень Розетский | |
| Карта физическая географическая | |
| Ключевое слово | |
| Ключевые слова символьных преобразований | |
| Комментарий | |
| Компилятор оптимизирующий | |
| Корень производной | |
| Корень уравнения | |
| Коэффициент ажиотажа | |
| Курс акций | |
| Линеаризация | |
| Линейная аппроксимация | |
| Линейное программирование | |
| Линейное целочисленное программирование | |
| Лицо, принимающее решения | |
| Лупа графика | 67, 82 |
| Массив переменных | |
| Мастер функций | 71 |
| Математическое моделирование | |
| Материализм диалектический | |
| Матрица | |
| Метод «два шага» поиска оптимума функции | |
| Метод «научного тыка» | |
| Метод Булириш-Штера | |
| Метод Гаусса-Зейделя | |
| Метод золотого сечения поиска оптимума функции | |
| Метод комбинированный Ньютона-секущих | |
| Метод Монте-Карло | |
| Метод наименьших квадратов | |
| Метод нормирующих множителей (коэффициентов) | |
| Метод Ньютона | |
| Метод перебора | |
| Метод половинного деления | |
| Метод последовательных приближений | |
| Метод Розенброка | |
| Метод Рунге-Кутта | |
| Метод секущих | |
| Метод статистических испытаний | |
| Метод стрельбы | |
| Метод Фибоначчи | |
| Метод штрафных санкций | |
| Метод Эйлера | |
| Методика преподавания | |
| Нелинейная аппроксимация | |
| Нелинейное программирование | |
| Нечеткая логика | |
| Нечеткое множество | |
| Обыкновенное дифференциальное уравнение | |
| Операнд оператора | |
| Оператор древовидный | |
| Оператор инфиксный | |
| Оператор постфиксный | |
| Оператор префиксный | |
| Оптимизация двухмерная | |
| Оптимизация многомерная | |
| Оптимизация одномерная | |
| Оптимизация программы | |
| Оптимум локальный | |
| Основная структурная теорема | |
| Отладка программы | |
| Ошибка методологическая | |
| Парапсихология | |
| Пасьянс | |
| Переменная глобальная | |
| Переменная локальная | |
| Переменная с индексом | |
| Переменная системная | |
| Пирамида финансовая | |
| Плата за кредит | |
| Полиморфизм | |
| Поп-арт | |
| Построение двухмерного графика («два шага») | |
| Построение трехмерного графика («семь шагов») | |
| Преобразование символьное | |
| Проверка ответа | |
| Производная | |
| Протяжка области графика | |
| Протяжка области документа | |
| Процент по вкладу | |
| Пуантилизм | |
| Пустышка в расчетах | |
| Размерность переменной | |
| Режим расчетов автоматический | |
| Режим расчетов ручной | |
| Рекурсия | |
| Рекурсия двусторонняя | |
| Рисунок на экране | |
| Рэкет | |
| Ряд бесконечный | |
| Ряд конечный | |
| Сглаживание функцией | |
| Сила Божья | |
| Сила лошадиная | |
| Симплекс-метод | |
| Система алгебраических уравнений | |
| Система банковская | |
| Система дифференциальных уравнений | |
| Система единиц измерения | |
| Система жестких дифференциальных уравнений | |
| Система искусственного интеллекта | |
| Система линейных алгебраических уравнений | |
| Система международная физических единиц | |
| Система солнечная | |
| Система счислений | |
| Слух музыкальный | |
| Слух программистский | |
| Сообщение об ошибке | |
| Сортировка | |
| Сплайн | |
| Стандартный справочник | |
| Счет устный | |
| Теория нечетких множеств | |
| Теория подобия | |
| Тип переменной | |
| Точка опорная | |
| Точность расчетов | |
| Трассировка графика | 68 |
| Учебник электронный | |
| Факториал | |
| Финансовая пирамида | |
| Функция виртуальная | |
| Функция вложенная | |
| Функция встроенная | |
| Функция двухмерная экспоненциальная | |
| Функция корней уравнения | |
| Функция Пауэла | |
| Функция принадлежности | |
| Функция Розенброка | |
| Функция тестовая | |
| Функция-вектор | |
| Функция-матрица | |
| Цвет на экране | |
| Цикл с выходом из середины | |
| Цикл с параметром | |
| Цикл с постпроверкой | |
| Цикл с предпроверкой | |
| Числа Аккермана | |
| Числа арабские | |
| Числа Мавроди | |
| Числа римские | |
| Числа Фибоначчи | |
| Числа Фибоначчи изящные | |
| Экзамен вступительный | |
| Эксперт | |
| Экстраполяция | |
| Эпидемия | |
| Язык BASIC | |
| Язык C | |
| Язык fortran | |
| Язык FRED | |
| Язык Pascal | |
| Якобиан | |
| Мастер 3-D диаграмм | 62 |
Именной указатель
| Finch Steven | |
| Truxal John | |
| Агата Кристи | 48 |
| Аккерман | |
| Бернулли | |
| Боровиков Игорь | |
| Брадис | 69 |
| Брудно А. | |
| Булириш | |
| Бюффон Ж.-Л.-Л. | 113 |
| Вийон Франсуа | 130 |
| Вирт Николаус | |
| Гаусс Карл Фридрих | |
| Гоголь Николай Васильевич | |
| Даниил Хармс | 23, 152 |
| Дейкстра Э. | |
| Жванецкий Михаил | 128 |
| Зверев, Анатолий | 123 |
| Зейдель | |
| Кальвин | 56 |
| Кемени, Джорж | 69 |
| Козьма Прутков | 114 |
| Корн Г. | 139 |
| Корн Т. | 139 |
| Коши | |
| Кутта | |
| Леня Голубков | |
| Лохвицкий | 129 |
| Лютер | 56 |
| Мавроди Сергей | |
| Малевич, Казимир | 118 |
| Марина Сергеевна | |
| Маяковский Владимир | 113 |
| Ньютон Исаак | |
| Оруэл, Джорж | 141 |
| Очкова Наталья | |
| Пауэл | 111 |
| Пирсон К. | 114 |
| Покровский Вадим | |
| Пушкин Александр Сергеевич | 56, 103, 120, 123, 147 |
| Роден, Огюст | 121 |
| Розенброк | 109 |
| Рунге | |
| Сливина Наталья | |
| Стерман Лев | |
| Толстой Лев Николаевич | |
| Тэффи | 129 |
| Усенко Василий | 138 |
| Фибоначчи | |
| Цвингли | 56 |
| Чапек Карел | 156 |
| Черчиль, Уинстон | 149 |
| Чехов Антон Павлович | 23, 47 |
| Шампольон, Жан-Франсуа | 34 |
| Шевченко Алексей | |
| Штёр | |
| Эйлер | |
| Эркюль Пуаро | 49 |