Аналитическое дифференцирование функции
3.1.1. Аналитическое дифференцирование функции
Для того чтобы аналитически найти производную функции f (х) в Mathcad:
1. Задайте функцию f (х).
2. Введите оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак <?>.
3. В появившихся местозаполнителях оператора дифференцирования (Рисунок 3.1) введите функцию, зависящую от аргумента х, т. е. f(х), и имя самого аргумента х.
4. Введите оператор <->> символьного вычисления для получения ответа (листинг 3.1).
Частные производные
3.4.1. Частные производные
Примеры отыскания частных производных функции двух переменных приведены в листингах 3.11 и 3.12. В первой строке обоих листингов определяется сама функция, а в последующих (символьным или численным образом) рассчитываются ее производные по обеим переменным — х и k. Чтобы определить частную производную в точке, необходимо предварительно задать значения всех аргументов, что и сделано в следующих строках листинга 3.12. Обратите внимание, что для символьного поиска производной функции нет необходимости задавать значения всех ее аргументов (третья строка листинга 3.12), а вот для численного дифференцирования (последняя строка листинга) должны быть предварительно определены все аргументы функции, иначе вместо результата появится сообщение об ошибке.
Дифференцирование в точке
3.2.1. Дифференцирование в точке
Для того чтобы численно продифференцировать функцию f (х) в некоторой точке, следует использовать оператор численного вывода (вместо символьного):
1. Определите точку х, в которой будет вычислена производная, например, х:=1.
2. Введите оператор дифференцирования и обычным образом введите имена функции и аргумента в местозаполнители (см. Рисунок 3.1).
3. Введите оператор = численного вывода результата.
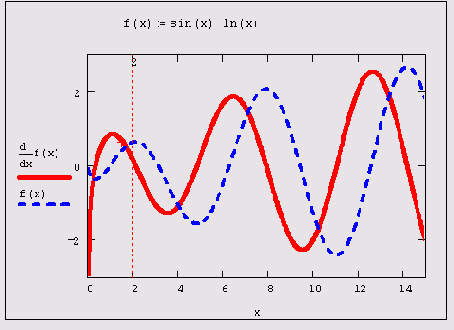
Пример дифференцирования функции f (x)=sin(x) ln(x) приведен в листинге 3.5.
Разложение в ряд при помощи меню
3.5.1. Разложение в ряд при помощи меню
Чтобы разложить некоторое выражение в ряд:
1. Введите выражение.
2. Выделите значение переменной, по которой требуется получить разложение в ряд.
3. Выполните команду Symbolics / Variable / Expand to Series (Символика / Переменная / Разложить в ряд) (Рисунок 3.12).
Об алгоритме дифференцирования
3.2.2. Об алгоритме дифференцирования
Для численного дифференцирования Mathcad применяет довольно сложный алгоритм, вычисляющий производную с колоссальной точностью до 7— 8-го знака после запятой. Погрешность дифференцирования не зависит от констант TOL или CTOL, в противоположность большинству остальных численных методов, а определяется непосредственно алгоритмом. Этот алгоритм (метод Риддера) описан во встроенной справочной системе Mathcad, доступной через меню Help (Справка). Мы не будем здесь его описывать, однако остановимся на важных аспектах численного определения производной функции f (х) на более простом примере. Несмотря на то, что простейшая разностная формула сильно отличается от метода Риддера, он все-таки поможет нам разобраться в некоторых вопросах, т. к. основан на базовом принципе численного дифференцирования, а именно на вычислении производной через значения функции f (х) в нескольких точках, расположенных на близком расстоянии друг от друга.
Исходя из определения производной функции, можно констатировать, что
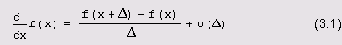
Основная проблема численного определения производной (как в этой простейшей формуле, так и в более сложных алгоритмах, в том числе Риддера) связана как раз с процедурой выбора значения Д, которая является далеко не очевидной. На первый взгляд может показаться, что следует выбирать очень малые Д, чтобы соблюсти желаемую точность, однако это не совсем так. Чтобы лучше разобраться в сути проблемы, используем Mathcad-программу, приведенную в листинге 3.6, которая рассчитывает (в зависимости от шага Д) погрешность разностной формулы (3.1). График полученной зависимости изображен на Рисунок 3.5, причем для его обеих осей выбран логарифмический масштаб, а сама производная (ради примера), согласно листингу 3.6, считается в одной точке х=1.
Оператор разложения в ряд
3.5.2. Оператор разложения в ряд
Для разложения в ряд альтернативным способом, с помощью оператора символьного вывода, используйте ключевое слово series, вставляя его одноименной кнопкой панели Symbolic (Символика). После ключевого слова series, через запятую, указывается имя переменной, по которой производится разложение, и порядок аппроксимации (листинги 3.21 и 3.22). Сравнить поведение исходной функции и нескольких ее разложений в ряд Тейлора (с разными порядками аппроксимации) можно по графику, приведенному на Рисунок 3.13.
Примеры градиент дивергенция и ротор
3.4.2. Примеры: градиент, дивергенция и ротор
Завершим разговор о частных производных несколькими примерами векторного анализа, которые нередко встречаются в вычислительной практике. Программная реализация первого из них, посвященная вычислению градиента функции двух переменных, приведена в листинге 3.14. В качестве примера взята функция f(x,y), определяемая в первой строке листинга, график которой показан на Рисунок 3.9, в виде линий уровня. Как известно, градиент функции f(x,y) является векторной функцией тех же аргументов, что и f (х,у), определенной через ее частные производные, согласно второй строке листинга 3.14. В его третьей строке производится аналитическое вычисление градиента, а в оставшейся части листинга задаются ранжированные переменные и матрицы, необходимые для подготовки графика линий уровня самой функции и графика векторного поля ее градиента (Рисунок 3.10).
Вычисление производной функции в точке
3.1.2. Вычисление производной функции в точке
Для того чтобы рассчитать производную в точке, необходимо предварительно задать значение аргумента в этой точке (листинг 3.2, вторая строка). Результатом дифференцирования в этом случае будет число — значение производной в этой точке. Если результат удается отыскать аналитически, то он приводится в виде числового выражения, а для того, чтобы получить его в форме числа, достаточно ввести после выданного выражения символ числового равенства <=> (последняя строка листинга 3.2).
Определение функций пользователя
3.1.3. Определение функций пользователя через оператор дифференцирования
Разумеется, оператор дифференцирования, как и любой другой, можно применять для определения собственных функций пользователя. В листинге 3.4 через производную от f (х) определяется еще одна пользовательская функция f(х), и затем, при помощи оператора символьного вывода, находится ее явный вид (предпоследняя строка листинга) и конкретное значение в точке х=1 (последняя строка).
Пример якобиан
3.4.3. Пример: якобиан
Еще одна задача, связанная с нахождением частных производных векторной функции, заключается в вычислении якобиана (или определителя матрицы Якоби) — матрицы, составленной из частных производных векторной функции по всем ее аргументам. Эта задача встречается в различных областях математики, например, применительно к жестким дифференциальным уравнениям (см. разд. 9.4). Приемы вычисления якобиана векторной функции f (х) векторного аргумента х демонстрируются в листинге 3.19. В нем для определения частных производных якобиана каждый i-й скалярный компонент f (x)i дифференцируется символьным процессором Mathcad.
Дифференцирование при помощи меню
3.1.4. Дифференцирование при помощи меню
Чтобы аналитически продифференцировать выражение по некоторой переменной, выделите в нем эту переменную и выберите команду Symbolics / Variable / Differentiate (Символика / Переменная / Дифференцировать) (Рисунок 3.3).
Аналитическое дифференцирование
3.1. Аналитическое дифференцирование
Вне всякого сомнения, вы по достоинству оцените возможности символьного процессора, позволяющего с легкостью выполнять рутинные вычисления производных громоздких функций. В отличие от всех других операций, символьное дифференцирование выполняется успешно для подавляющего большинства аналитически заданных функций. Думаю, что многие читатели, которым иногда приходится аналитически дифференцировать функции, как и автор этих строк, единожды попробовав сделать это в среде Mathcad, уже никогда не возьмут в руки карандаша для расчета производных "вручную".
Аналитическое дифференцирование по переменной
Рисунок 3.3. Аналитическое дифференцирование по переменной

В результате, в следующей строке за выражением появится значение ее производной. Для того чтобы найти вторую производную, повторно примените эту последовательность действий, но уже к полученному результату дифференцирования. Так же находятся и производные высших порядков.
Аналитическое разложение выражения в ряд по переменной х
Рисунок 3.12. Аналитическое разложение выражения в ряд по переменной х

4. В появившемся диалоговом окне Expand to Series (Разложить в ряд) введите желаемый порядок аппроксимации (Order of Approximation) и нажмите кнопку ОК.
Результат разложения появится под выражением (он показан на Рисунок 3.12, внизу).
Примечание 1
Примечание 1
Не забывайте, что разложение строится только в точке х=0. Чтобы получить разложение в другой точке х=а, можно, к примеру, подставить вместо переменной х значение х-а.
Частные производные
3.4. Частные производные
С помощью обоих процессоров Mathcad можно вычислять производные функций не только одного, но и любого количества аргументов. Как известно, производные функции нескольких аргументов по одному из них называются частными. Чтобы вычислить частную производную, необходимо, как обычно, ввести оператор производной с панели Calculus (Вычисления) и в соответствующем местозаполнителе напечатать имя переменной, по которой должно быть осуществлено дифференцирование.
Численное дифференцирование
3.2. Численное дифференцирование
Вычислительный процессор Mathcad обеспечивает превосходную точность численного дифференцирования.
Дифференцирование
Дифференцирование
Операция дифференцирования реализована в Mathcad как в численной, так и в аналитической форме и обозначается при помощи традиционного оператора, т. е. соответствующими математическими символами (подобно сложению или умножению). Если расчеты выполняются с помощью вычислительного процессора, необходимо хорошо представлять себе особенности численного алгоритма, действие которого остается для пользователя "за кадром". С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, причем как функции, так и аргументы могут быть и действительными, и комплексными.
Если производная функции в данной
Рисунок 3.6. Если производная функции в данной точке не существует, выдается сообщение об ошибке

Если попробовать численно определить производную очень близко к нулю, например, при х=10-100, то, несмотря на существование производной, может появиться сообщение об ошибке "Can't converge to a solution" (Невозможно найти решение). Новые версии Mathcad (начиная с 11-й) справляются с указанной трудностью, поскольку в них даже для численного дифференцирования сначала задействуется символьный процессор, поставляющий аналитическое решение, подстановка в которое аргумента дифференцирования дает верный результат. Встретившись с одной из упомянутых ошибок, присмотритесь внимательнее к дифференцируемой функции и убедитесь, что вы не имеете дело с точкой сингулярности.
График производной функции
Рисунок 3.2. График производной функции
Примечание 1
Примечание 1
Помните о том, что в описанном применении оператора дифференцирования его результатом является функция той же переменной х. Пример визуализации операции дифференцирования с помощью графика приведен на Рисунок 3.2.
Примечание 2
Примечание 2
Исходная функция может зависеть не только от аргумента х, но и от других аргументов, например f(x,y,z,t) и т. п. В этом случае дифференцирование производится точно так же, причем становится более понятной необходимость определения переменной дифференцирования (в нижнем местозаполнителе оператора дифференцирования). Расчеты производных по разным аргументам (в этом случае говорят о частных производных), разумеется, будут давать совершенно разные результаты (см. разд. 3.4.).
График разложений функции в ряд
Рисунок 3.13. График разложений функции в ряд в зависимости от порядка аппроксимации (продолжение листинга 3.21)
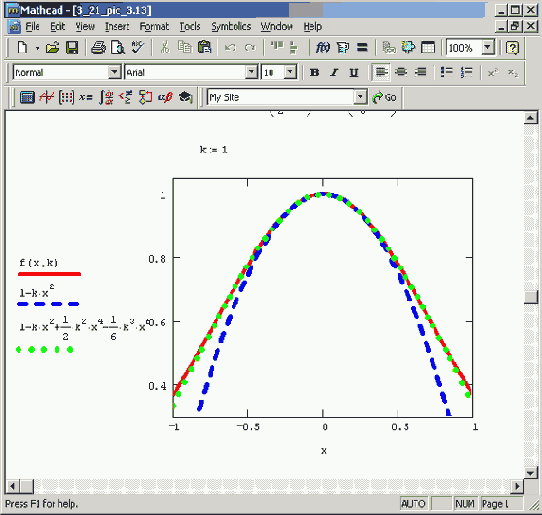
Видно, что разложение в ряд хорошо работает в окрестности точки х=0, а по мере удаления от нее все сильнее и сильнее отличается от функции. Естественно, что чем выше порядок аппроксимации, тем ближе к исходной функции располагается соответствующее разложение Тейлора.
График точности формулы (3 1)
Рисунок 3.5. График точности формулы (3.1) в зависимости от шага дельта (продолжение листинга 3.6)

Если увеличение ошибки на правом конце графика является совершенно очевидным, поскольку, согласно формуле (3.1), чем больше А, тем больше погрешность, то рост ошибки при очень малых Д может, на первый взгляд, показаться неожиданным. Однако все дело в том, что, применяя разностную формулу, мы неявно полагали, что умеем точно вычислять значения функции f (х) в любой точке. Между тем, любые компьютерные вычисления сопряжены с неустранимыми погрешностями, в частности, обусловленными дискретным представлением чисел. Поэтому в реальности мы можем вычислить значение f (х) лишь с некоторой погрешностью 8, обусловленной (по крайней мере) заведомым округлением чисел при расчетах на компьютере.
В результате, при очень малом шаге разностные формулы означают вычитание друг из друга близких чисел. В этом случае ошибки вычисления функции f (х) становятся доминирующими и приводят к существенному росту суммарной погрешности вычисления разностной производной. Отсюда как раз и следует тот вывод, что значение шага следует выбирать "не очень малым", иначе ошибки вычисления f (х) неминуемо сделают результат дифференцирования неправильным. Глядя на Рисунок 3.5, легко сообразить, что в данном случае следует выбирать промежуточные значения Д, которые обеспечат минимальную (или почти минимальную) погрешность.
Следует подчеркнуть, что в зависимости от характера дифференцируемой функции диапазон приемлемых значений Л будет различным. Поэтому в каждом конкретном случае требуется совершать дополнительные шаги, тестирующие верность выбора шага для численного дифференцирования. Такая процедура, кстати говоря, заложена в адаптивном алгоритме дифференцирования, примененном в Mathcad, что делает его весьма надежным для численного расчета производной.
С учетом сказанного выше, с дифференцированием в Mathcad обычно не возникает сложных проблем. Исключение составляют функции, которые дифференцируются в окрестности сингулярной точки; например, для функции f (х)=1/х это будут точки вблизи х=0. При попытке найти ее производную при х=0 (Рисунок 3.6) будет выдано сообщение об одной из ошибок деления на ноль "Can't divide by zero" (Деление на ноль невозможно) или "Found a singularity while evaluating this expression. You may be dividing by zero" (Найдена сингулярность при вычислении этого выражения. Возможно, вы делите на ноль).
Иллюстрирует пример векторной
Рисунок 3.11 иллюстрирует пример векторной функции f (х,у) (определяемой в первой строке листинга) и вычисление ее дивергенции (которое производится аналитически в третьей строке). Обратите внимание, что в качестве исходной вектор-функции взят результат предыдущих расчетов, показанный (в форме векторного поля) на Рисунок 3.10. Строки кода в верхней части Рисунок 3.11 нужны для подготовки графика вычисленной дивергенции (в виде трехмерной поверхности и линий уровня, соответственно сверху и снизу).
Точно такую же структуру имеют расчеты ротора той же векторной функции f (х,у) в листинге 3.16, причем определение операции взятия ротора приводится в его второй строке (как и в случае дивергенции для листинга 3.15).
Читателю, знакомому с векторным анализом, предлагается догадаться самому, почему в рассматриваемом примере (листинги 3.14—3.16) ротор получается тождественно равным нулю (последняя строка листинга 3.16).
Примечание 1
В электронной книге Resource Center (Центр ресурсов), поставляемой вместе с Mathcad, вы найдете дополнительные примеры вычисления градиента, дивергенции и ротора, относящихся к трехмерному случаю.
Изменение вида оператора дифференцирования
Рисунок 3.8. Изменение вида оператора дифференцирования
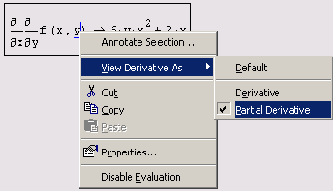
Для того чтобы изменить вид оператора дифференцирования на представление частной производной, следует:
1. Вызвать контекстное меню из области оператора дифференцирования нажатием правой кнопки мыши.
2. Выбрать в контекстном меню верхний пункт View Derivative As (Показывать производную как).
3. В появившемся подменю (Рисунок 3.8) выбрать пункт Partial Derivative (Частная производная).
Чтобы вернуть вид производной, принятый по умолчанию, выберите в подменю пункт Default (По умолчанию) либо, для представления ее в обычном виде, — Derivative (Производная).
Пример аналитического дифференцирования
Листинг 3.1. Пример аналитического дифференцирования
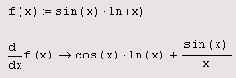
Аналитическое дифференцирование функции в точке
Листинг 3.2. Аналитическое дифференцирование функции в точке

Для того чтобы продифференцировать функцию, вовсе не обязательно предварительно присваивать ей какое-либо имя, как это сделано в листингах 3.1, 3.2. Можно определить функцию непосредственно в операторе дифференцирования (это демонстрирует первая строка листинга 3.3).
Правильное и неправильное
Листинг 3.3. Правильное и неправильное использование оператора дифференцирования

Как вы заметили, оператор дифференцирования, в основном, соответствует его общепринятому математическому обозначению, и поэтому его легко использовать интуитивно. Однако в некоторых случаях при вводе оператора дифференцирования следует проявить осторожность. Рассмотрим один показательный пример, приведенный во второй строке листинга 3.3, который демонстрирует неправильное применение оператора дифференцирования для вычисления производной в точке. Вместо вычисления производной sin(x) при х=2, как этого можно было ожидать, получено нулевое значение. Это случилось из-за того, что аргумент функции sin(x) введен не в виде переменной х, а в виде числа. Поэтому Mathcad воспринимает последнюю строку как вычисление сначала значения синуса в точке х=2, а затем дифференцирование этого значения (т. е. константы) также в точке х=2, в соответствии с требованием первой строки листинга. Поэтому ответ, на самом деле, неудивителен — в какой точке ни дифференцируй константу, результатом будет ноль.
Примечание 1
Примечание 1
То же самое касается и операции численного дифференцирования, т. е. применения оператора <=>
вместо <->
>
.
Определение функции
Листинг 3.4. Определение функции посредством оператора дифференцирования

Численное дифференцирование функции в точке
Листинг 3.5. Численное дифференцирование функции в точке

ВНИМАНИЕ!
Не забывайте предварительно определять точку, в которой производится численное дифференцирование, как это сделано во второй строке листинга 3.5. Иначе будет выдано сообщение об ошибке, показанное на Рисунок 3:4, гласящее, что переменная или функция, входящая в выражение, ранее не определена. Между тем, символьное дифференцирование (см. разд. 3.1) не требует обязательного явного задания точки дифференцирования. В этом случае вместо значения производной (числа или числового выражения) будет выдана аналитическая зависимость (см. листинг 3.1).
Расчет зависимости
Листинг 3.6. Расчет зависимости точности разностной формулы от шага

демонстрирует численное
Листинг 3.7 демонстрирует численное и символьное вычисление второй производной функции в заданной точке. Обратите внимание, что, как и при вычислении обычной производной, необходимо перед оператором дифференцирования присвоить аргументу функции значение, для которого будет вычисляться производная. А вот для аналитического нахождения производных высших порядков при помощи оператора символьного вывода (в полном соответствии с разд. 3.1), вводить значения аргумента не следует (листинг 3.8).
Пример вычисления
Листинг 3.7. Пример вычисления второй производной функции в точке

Пример аналитического
Листинг 3.8. Пример аналитического поиска второй производной функции

Примечание 1
Примечание 1
Убедиться в том, что символьный процессор Mathcad в последней строке листинга 3.7 дает тот же результат, что и вычислительный процессор в предыдущей строке, можно, упростив его. Для этого следует выделить полученное последнее выражение и выбрать в меню Symbolics (Символика) пункт Simplify (Упростить). После этого ниже появится еще одна строка с численным результатом выделенного выражения.
Повторимся, что численный метод предусматривает возможность вычисления производных до 5-го порядка, а символьный процессор умеет считать производные произвольного порядка (конечно, если аналитическое решение задачи в принципе существует). Сказанное иллюстрирует листинг 3.9, в котором аналитически вычисляется шестая производная функции, а попытка численного вывода результата того же выражения приводит к ошибке.
Численное и символьное
Листинг 3.9. Численное и символьное вычисление шестой производной

Чтобы вычислить производную порядка выше 5-го численно, можно последовательно применить несколько раз оператор м-й производной (листинг 3.10), подобно тому, как производится отыскание кратных интегралов (см. разд. 4.3.4). Однако следует помнить о том, что численное определение производных высших порядков производится тем же вычислительным методом Риддера, что и для первых производных. Поскольку, как уже было сказано, для первой производной этот метод обеспечивает точность до 7—8 значащих разрядов числа, при повышении порядка производной на каждую единицу точность падает примерно на один разряд.
ВНИМАНИЕ!
Из сказанного ясно, что падение точности при численном расчете высших производных может быть очень существенно. В частности, если попытаться определить шестую производную функции l/х, то в качестве результата будет выдан ноль, в то время как истинное значение девятой производной может быть найдено при помощи символьного процессора (листинг 3.10).
Попытка численного
Листинг 3.10. Попытка численного поиска шестой производной функции в точке дает неправильный результат
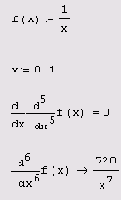
Аналитическое вычисление частных производных
Листинг 3.11. Аналитическое вычисление частных производных
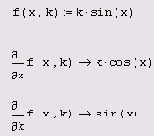
Символьное и численное
Листинг 3.12. Символьное и численное вычисления частных производных в точке

Частные производные высших порядков рассчитываются точно так же, как и обычные производные высших порядков (см. разд. 3.3).
иллюстрирует расчет
Листинг 3.13 иллюстрирует расчет вторых производных функции по переменным х и у, а также смешанной производной.
Вычисление второй частной производной
Листинг 3.13. Вычисление второй частной производной

Возможно, вы обратили внимание, что во всех трех листингах 3.11—3.13 оператор дифференцирования записан в традиционной форме частной производной (с округлыми символами дифференциала). Запись оператора не влияет на вычисления, а служит лишь более привычной формой представления расчетов.
Вычисление градиента функции двух переменных
Листинг 3.14. Вычисление градиента функции двух переменных

Вычисление дивергенции векторной функции
Листинг 3.15. Вычисление дивергенции векторной функции
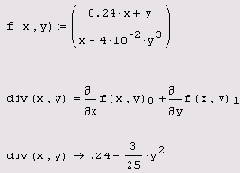
Если, как принято в математике, обозначить оператор взятия градиента символом V, то дивергенцию вектор-функции можно формально определить как скалярное произведение Vf, а еще одну распространенную операцию векторного анализа — ротор (или, по-другому, вихрь или завихренность) — как векторное произведение Vxf.
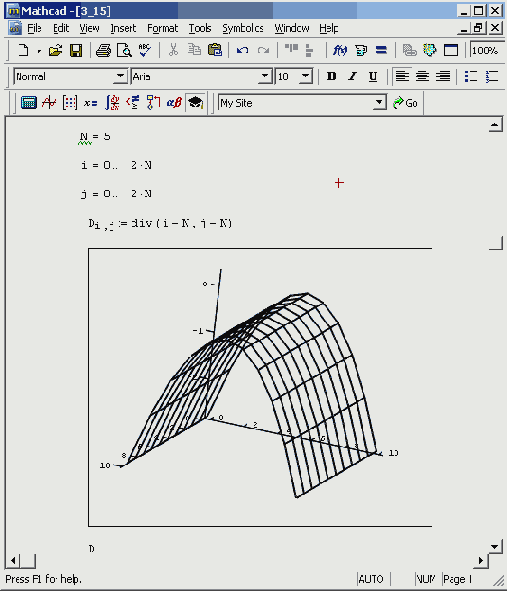
Градиент функции трех переменных
Листинг 3.17. Градиент функции трех переменных

Дивергенция и ротор в трехмерном пространстве
Листинг 3.18. Дивергенция и ротор в трехмерном пространстве
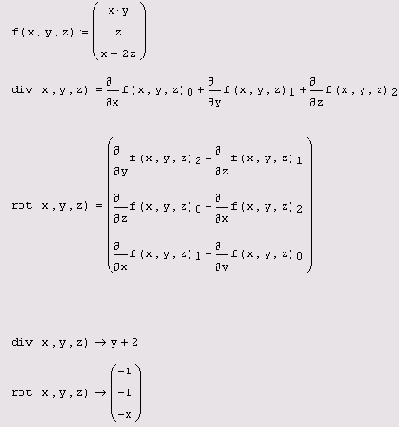
Вычисление якобиана
Листинг 3.19. Вычисление якобиана векторной функции векторного аргумента

Тот же самый якобиан можно вычислить и несколько по-другому, если определить функцию не одного векторного, а трех скалярных аргументов f(x,y,z) (листинг 3.20). Не забывайте, что для численного определения якобиана необходимо сначала определить точку, в которой он будет рассчитываться, т. е. вектор х в терминах листинга 3.19, или все три переменных х, у, z в обозначениях листинга 3.20.
Вычисление якобиана
Листинг 3.20. Вычисление якобиана векторной функции трех скалярных аргументов

Разложение функций
Листинг 3.21. Разложение функций в ряд с разным порядком аппроксимации

Разложение функции
Листинг 3.22. Разложение функции нескольких переменных в ряд по разным переменным

Модельная функция двух переменных
Рисунок 3.9. Модельная функция двух переменных (продолжение листинга 3.14)

Оператор дифференцирования
Рисунок 3.1. Оператор дифференцирования

Оператор производной высшего порядка
Рисунок 3.7. Оператор производной высшего порядка

Очевидно, что "производная" при N=0 по определению равна самой функции, при N=1 получается обычная первая производная.
Ошибка в применении оператора
Рисунок 3.4. Ошибка в применении оператора дифференцирования (не задан аргумент)

Примечание 1
Примечание 1
В Mathcad 11 и выше для ускорения и повышения точности численного дифференцирования функций, заданных аналитически, автоматически задействуется символьный процессор. Сначала предпринимается попытка отыскать производные, входящие в выражение, аналитически, а уже затем, если она оказывается неудачной, включается в работу численный метод.
Производные высших порядков
3.3. Производные высших порядков
Mathcad позволяет численно определять производные высших порядков, от 3-го до 5-го включительно. Чтобы вычислить производную функции f (х) N-го порядка в точке х, нужно проделать те же самые действия, что и при взятии первой производной (см. разд. 3.1 и 3.2), за тем исключением, что вместо оператора производной необходимо применить оператор м-й производной (Nth Derivative). Этот оператор вводится с той же панели Calculus (Вычисления), либо с клавиатуры нажатием клавиш <Ctrl>+<?>, и содержит еще два дополнительных местозаполнителя (Рисунок 3.7), в которые следует поместить число N. В полном соответствии с математическим смыслом оператора, определение порядка производной в одном из местозаполнителей приводит к автоматическому появлению того же числа в другом из них.
Разложение функции в ряд Тейлора
3.5. Разложение функции в ряд Тейлора
Еще одна операция, тесно связанная с дифференцированием, представляет собой разложение функции в ряд Тейлора по любой переменной х в некоторой точке. Если эта точка х=0, то ряд называют также рядом Маклорена, и он представим в окрестности точки х=0 суммой вида a0+a1x+a2x2+a3x3+... Здесь ai — некоторые коэффициенты, не зависящие от х, но, возможно, являющиеся функциями других переменных, от которых зависит исходная функция. Именно эти коэффициенты выражаются через производные функции. Если она имеет в точке х=0 особенность, то соответствующее разложение называют рядом Лорана.
При поиске разложения в ряд Тейлора нет необходимости явно рассчитывать все его коэффициенты, поскольку эта операция предусмотрена разработчиками Mathcad и выполняется при помощи символьного процессора. При этом можно использовать для ее осуществления как соответствующие встроенные функции, так и меню Symbolics (Символика).
Векторное поле градиента функции
Рисунок 3.10. Векторное поле градиента функции двух переменных (продолжение листинга 3.14)

Как можно убедиться, сравнив графики на Рисунок 3.9 и 3.10, математический смысл градиента состоит в задании в каждой точке (х,у) направления на плоскости, в котором функция f (х,у) растет наиболее быстро. Абсолютное значение градиента (т. е. длина вектора в каждой точке) определяет локальную скорость изменения f (x,y). Из сопоставления графи ков ясно, что в центре показанной на них области (х,у) сама функция f (х,у) меняется медленно (соответственно, значения ее градиента являются малыми), а в углах — быстро (там значения градиента максимальны).
Очень важно заметить, что градиент является не скалярной, а векторной функцией переменных х,у, поскольку фактически представляет собой комбинацию двух функций, задающих соответствующие проекции (горизонтальную и вертикальную) вектора в каждой точке. До сих пор в данной главе мы рассматривали дифференцирование скалярных функций, однако в математике часто приходится иметь дело и с вычислением производных векторных функций. Рассмотрим эти действия на примере операции поиска дивергенции (листинг 3.15 и Рисунок 3.11), применимой к векторному полю, т. е. векторной функции, зависящей от пространственных координат (на плоскости, как в нашем примере, или в трехмерном пространстве).