Метод секущих функция root
5.3.1. Метод секущих: функция root
Итерационный алгоритм, реализованный в функции root, который называется методом секущих, состоит в следующем (Рисунок 5.7):
1. Начальное приближение принимается за 0-е приближение к корню: х0=х.
2. Выбирается шаг h=TOLх и определяется первое приближение к корню x1=x0+h. Если х=0, то принимается h=TOL.
3. Через эти две точки проводится секущая — прямая линия, которая пересекает ось х в некоторой точке х2. Эта точка принимается за второе приближение.
4. Новая секущая проводится через первую и вторую точки, тем самым определяя третье приближение, и т. д.
5. Если на каком-либо шаге оказывается, что уравнение выполнено, т. е. |f (х)|<TOL, то итерационный процесс прерывается, и х выдается в качестве решения.
Системы уравнений функция Find
5.2.1. Системы уравнений: функция Find
Рассмотрим решение системы N нелинейных уравнений с м неизвестными
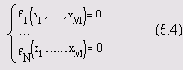
Здесь f1(x1, ..., хM), ..., fN (x1, ..., XM) — некоторые скалярные функции от скалярных переменных x1,x2, ..., хM и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (5.4) можно формально переписать в виде
f(x)=0, (5.5)
где х — вектор, составленный из переменных x1,x2, ... ,хM, a f (х) — соответствующая векторная функция.
Вычислительный блок Given /Find
Для численного решения систем уравнений применяется тот же самый вычислительный блок, что и для символьных вычислений (см. разд. 5.1.1). Повторимся, что он состоит из ключевого слова Given, самой системы уравнений, записанной при помощи логических операторов панели Boolean (Булевы операторы), а также встроенной функции Find. Find(x1, ... ,хM) — встроенная функция для решения системы алгебраических уравнений и неравенств относительно переменных x1,...,xM. Значение функции Find представляет собой вектор, составленный из решений по каждой переменной.
Примечание 1
Примечание 1
Встроенная функция Find использует в качестве численного алгоритма один из градиентных методов (см. разд. 5.3). Этот факт налагает некоторые ограничения на уравнения системы, которые должны быть достаточно гладкими функциями своих аргументов.
Примечание 2
Примечание 2
При численных расчетах может быть найден только один из корней уравнения, в отличие от символьных вычислений, которые позволяют определить все имеющиеся корни.
Применение численного нахождения корней отличается от символьного двумя обстоятельствами:
вместо оператора символьного вывода после функции Find следует использовать оператор численного вывода (знак равенства); перед вычислительным блоком Given/Find должны быть заданы начальные значения (guess value) для всех неизвестных, т. е. всем переменным x1, ... ,хM, относительно которых решается уравнение, следует предварительно присвоить некоторые численные значения, с которых и будет начинаться поиск корня. Таким образом, присвоение начального значения требует априорной информации о примерном местонахождении корня и связано с проблемой локализации корней, упомянутой в начале разд. 5.2.
Примечание 3
Примечание 3
Помните также о том, что, в отличие от символьного, для численного процессора необходимо задать числовые значения всех параметров, входящих в уравнение.
Одно уравнение с одним неизвестным
Рассмотрим в качестве примера (листинг 5.8) одно уравнение с одним неизвестным, которое уже решалось нами аналитически (см. листинги 5.1 и 5.2). Уравнение имеет три корня, как видно из графика, приведенного на Рисунок 5.4. Обратите внимание, что перед ключевым словом Given переменной х присваивается некоторое значение х=1. В остальном применение функции Find для решения уравнения не отличается от символьных расчетов.
Вычислительный блок Given/Find
5.1.1. Вычислительный блок Given/Find
Рассмотрим решение системы N нелинейных уравнений с м неизвестными

Здесь fi(xi, ..., хM) =b1, . .., fN (xi, ..., хM) =bN — некоторые скалярные выражения, зависящие от скалярных переменных x1,x2, ... ,хM и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (5.1) можно формально переписать в- виде
f(x)=b, (5.2)
где х — вектор, составленный из переменных x1,x2,.. . ,хN, b — вектор, составленный из правых частей уравнений, a f (х) — соответствующая векторная функция их левых частей.
Для решения систем в Mathcad применяется специальный вычислительный блок Given/Find (Дано/найти), состоящий из трех частей, идущих последовательно друг за другом:
Given — ключевое слово; система, записанная логическими операторами в виде равенств и, возможно, неравенств; Find(xi, . .. ,хм) — встроенная функция для решения системы уравнений относительно переменных x1, ..., хM.
Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры, помните, что логический знак равенства вводится сочетанием клавиш <Ctrl>+<=>. Значение функции Find представляет собой матрицу, составленную из всевозможных решений по каждой переменной, причем количество ее строк в точности равно числу аргументов Find. Структура матрицы решения станет сразу вам понятной, как только вы бросите взгляд на примеры, приведенные ниже в данном разделе.
Примечание 1
Примечание 1
При решении уравнений в векторной форме в вычислительном блоке не рекомендуется, а, начиная с версии Mathcad 12, просто запрещено использование одних элементов вектора в качестве неизвестных, а других — в качестве параметров задачи. Соответствующие примеры, иллюстрирующие данное ограничение, вы найдете на компакт-диске.
Градиентные методы функция Find
5.3.2. Градиентные методы: функция Find
Если вы решаете "хорошие" уравнения, как все те, которые были приведены в предыдущих разделах, то, вообще говоря, можете никогда не задумываться, как именно Find ищет их корни. Однако даже в этом случае полезно представлять, что происходит "за кадром", т. е. какие действия совершаются в промежутке между введением необходимых условий после ключевого слова Given и получением результата после применения функции Find. Это важно хотя бы с позиций выбора начальных значений переменных перед вычислительным блоком. Рассмотрим в данном разделе некоторые особенности численных методов и возможности установки их различных параметров, которые предоставляет Find.
Принцип действия градиентных алгоритмов
Во встроенной функции Find реализовано несколько градиентных численных алгоритмов, один из которых может выбрать либо программа Mathcad, либо сам пользователь. Покажем их основную идею на примере уравнения с
одним неизвестным f (x)=0 для функции f(х)=х2+5х+2, график которой показан на Рисунок 5.8. Принцип градиентных методов состоит в последовательных приближениях к истинному решению уравнения, которые вычисляются с помощью производной от f (х). Приведем наиболее простую форму алгоритма, называемого методом Ньютона:
1. За нулевую итерацию принимается введенное пользователем начальное значение х0=х.
2. В точке х0 методом конечных разностей вычисляется производная f (x0).
3. Пользуясь разложением Тейлора, можно заменить f (х) в окрестности х0 касательной — прямой линией f (x)=f (x0) +f (х0)-(х-х0).
4. Определяется точка x1, в которой прямая пересекает ось х (Рисунок 5.8).
5. Если f (x1)<TOL, то итерации прерываются, и значение x1 выдается в качестве решения. В противном случае x1 принимается за новую итерацию, и цикл повторяется: строится касательная к f (х) в точке x1, определяется х2 — точка ее пересечения с осью х и т.д.
Одно уравнение
5.1.2. Одно уравнение
Поясним сказанное на примере решения одного (кубического) уравнения с одним неизвестным х (Рисунок 5.1):
Зх3+2х2-7х=0. (5.3)
Уравнение с одним неизвестным функция root
5.2.2. Уравнение с одним неизвестным: функция root
Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.
root(f(x),x); root (f (x) , x, a, b);
f(x) — скалярная функция, определяющая уравнение f(x)=0; х — имя скалярной переменной, относительно которой решается уравнение; а, b — границы интервала, внутри которого происходит поиск корня.
Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.
Корни полинома функция polyroots
5.2.3. Корни полинома: функция polyroots
Если функция f (х) является полиномом, то все его корни можно определить, используя встроенную функцию:
polyroots(v)
где v — вектор, составленный из коэффициентов полинома.
Поскольку полином N-й степени имеет ровно N корней (некоторые из них могут быть кратными), вектор v должен состоять из N+1 элемента. В основе встроенной функции polyroots лежат специфические численные алгоритмы, а результатом ее действия является вектор, составленный из N корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root. Пример поиска корней полинома четвертой степени иллюстрируется листингом 5.16.
Коэффициенты рассматриваемого в примере полинома
f (х) = (х-3)-(х-1)3=х4-6х3+12х2-10х+3
записаны в виде вектора в первой строке листинга. Первым в векторе должен идти свободный член полинома, вторым — коэффициент при х1 и т. д. Соответственно, последним N+1элементом вектора должен быть коэффициент при старшей степени xN.
СОВЕТ
Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пункт Expand (Разложить). В результате символьный процессор Mathcad сам преобразует полином в нужную форму; пользователю надо будет только корректно ввести ее в аргументы функции polyroots.
Метод продолжения по параметру
5.3.3. Метод продолжения по параметру
Решение "хороших" нелинейных уравнений и систем типа тех, которые были рассмотрены в предыдущих разделах этой главы, представляет собой несложную, с вычислительной точки зрения, задачу. В реальных инженерных и научных расчетах очень распространена более сложная проблема: решение не одного уравнения (или системы), а целой серии уравнений, зависящих от некоторого параметра (или нескольких параметров). Для таких задач существуют очень эффективные методы, которые называются методами продолжения. Эти методы непосредственно не встроены в Mathcad, но могут быть легко запрограммированы с помощью уже рассмотренных нами средств. Будем далее говорить об одном уравнении, имея в виду, что всегда возможно обобщение результатов на случай системы уравнений.
Пусть имеется уравнение f (а,х)=0, зависящее не только от неизвестного х, но и от параметра а. Требуется определить зависимость его корня х от параметра а, т. е. х(а). Простой пример такой задачи был приведен в листинге 5.3 (см. разд. 5.1.2). Тогда нам повезло, и решение в общем виде было найдено с помощью символьных вычислений. Рассмотрим еще один, чуть более сложный, пример алгебраического уравнения, зависящего от параметра а следующим образом: ln(ах2)=х (Рисунок 5.11).
Системы уравнений
5.1.3. Системы уравнений
Символьное решение системы алгебраических уравнений отличается от описанного случая одного уравнения только количеством соотношений, задаваемых после ключевого слова Given. Соответственно, число неизвестных также может быть любым, причем необязательно равным числу уравнений. Если система уравнений имеет не обособленные решения, а целые семейства решений, то соответствующие результаты выдаются символьным процессором Mathcad в виде выражений, формально зависящих от одной из переменных как от параметра (пример решения одного уравнения с тремя неизвестными был приведен ранее в последних двух строках листинга 5.3).
Решение системы двух нелинейных уравнений иллюстрирует листинг 5.7. Нахождение символьным процессором его обоих корней визуализируется на графике, приведенном на Рисунок 5.2. На нем каждое из уравнений показывается в виде зависимости у(х): первое — сплошной кривой, а второе — пунктиром. Поскольку первое уравнение является квадратичным, то оно определяет на плоскости XY параболу, и поскольку второе уравнение линейное, то оно соответствует на графике прямой линии. Очевидно, что две точки пересечения кривых соответствуют одновременному выполнению обоих уравнений, т. е. их координаты равны искомым действительным корням системы.
Локализация корней
5.2.4. Локализация корней
Чтобы решить задачу предварительной (грубой) локализации корней, в самых простых случаях можно использовать графическое представление f (х) (см. Рисунок 5.1, 5.2 и 5.4). Понятно, что в случае многомерных систем такой способ практически неприменим. Если требуется исследовать определенную область определения переменных уравнения на наличие корней, определив их примерное положение, то обычно применяют весьма расточительный способ, называемый сканированием. Оно состоит в последовательном поиске корня, начиная из множества пробных точек, покрывающих расчетную область.
Обычно (вне Mathcad) сканирование организуют следующим образом. Область определения функции разбивается на элементарные области (в случае функции двух переменных чаще всего прямоугольные, в случае трех переменных — кубические и т. д.). Из центра каждой элементарной области запускается численный метод поиска корня, и в случае выхода итераций за ее пределы расчеты прерываются, а в противном случае происходит нахождение корня. Гораздо менее надежной (но зато более экономной) альтернативой является простое вычисление и сравнение между собой невязок системы уравнений в центральных точках элементарных областей. На тех участках области определения, где норма невязки невелика, вероятность локализации корня больше, и именно из локальных минимумов нормы невязки можно запускать градиентный метод для уточнения корня.
Пример организации упрощенного варианта сканирования по одной переменной приведен на Рисунок 5.6. График функции, корни которой подлежат определению, показан в его верхней части. Затем осуществляется решение уравнения при помощи функции root, для нескольких последовательно расположенных узлов. Результат выдается в последней строке листинга в виде таблицы, из которой видно, что на рассматриваемом интервале уравнение имеет три корня.
Примечание 1
Примечание 1
Конечно, гарантии, что все существующие корни будут найдены, особенно в многомерных случаях, чаще всего нет. Всегда существует вероятность "просмотреть" корень, расположенный между узлами сканирования.
Решение уравнений при помощи меню
5.1.4. Решение уравнений при помощи меню
Аналитическое решение алгебраического уравнения можно получить и при помощи меню. Данный способ удобно применять, когда уравнение записано в форме математического выражения (зависящего, возможно, от различных переменных), и требуется вычислить аналитически значение одной переменной, при котором выражение обращается в ноль. Для этого:
1. Введите выражение.
2. Выделите переменную, относительно которой будет решаться уравнение, приравнивающее выражение нулю.
3. Выберите в меню Symbolics (Символика) пункт Variable/Solve (Переменная/Решить) (Рисунок 5.3).
Численное решение уравнений
5.2. Численное решение уравнений
Как правило, отыскание корней алгебраического уравнения (или системы уравнений) численными методами связано с двумя задачами:
локализация корней, т. е. определение их существования в принципе, а также исследование их количества и примерного расположения; собственно отыскание корней с заданной погрешностью (в Mathcad ее роль играет системная константа TOL).
Последнее означает, что надо найти значения х0, при которых f(х0) отличается от нуля не более чем на TOL. Почти все встроенные функции системы Mathcad, предназначенные для решения нелинейных алгебраических уравнений (в том числе функция Find применительно к численному процессору) нацелены на решение второй задачи, т. е. предполагают, что корни уже приблизительно локализованы. Иными словами, перед тем, как непосредственно приступать к нахождению корней уравнения, необходимо (хотя бы приблизительно) представлять себе, где они находятся. Имея в виду данную оговорку, мы перейдем к рассмотрению второй из задач, а проблему предварительной локализации корней рассмотрим в конце данного раздела.
Диалоговое окно Advanced Options
Рисунок 5.10. Диалоговое окно Advanced Options

Во второй строке — Variable estimation (Аппроксимация переменных) — можно определить тип аппроксимации рядом Тейлора. Для рассмотренного нами в этом разделе случая аппроксимации касательной прямой линией выберите переключатель Tangent (Касательная), для более точной квадратичной аппроксимации (параболой) выберите Quadratic (Квадратичная). Следующая группа переключателей — Linear variable check (Проверка линейности) — позволяет в специфических задачах сэкономить время вычислений. Если вы уверены, что нелинейности всех функций, входящих в уравнение, мало сказываются на значениях всех их частных производных, то установите переключатель Yes (Да). В этом случае производные будут приняты равными константам и не будут вычисляться на каждом шаге.
ВНИМАНИЕ!
С осторожностью изменяйте параметры численных методов. Пользуйтесь ими, когда решение не находится при выставленных по умолчанию параметрах, или когда расчеты занимают очень продолжительное время.
Пара переключателей Multistart (Сканирование) задает опцию поиска глобального или локального минимума или максимума. Если выставлен переключатель Yes (Да), Mathcad будет пытаться найти наиболее глубокий экстремум из области, близкой к начальному приближению. Эта опция предназначена, в основном, для настройки (тех же самых градиентных) алгоритмов поиска экстремума, а не для решения алгебраических уравнений (см. главу 6).
Наконец, последний переключатель — Evolutionary (Эволюционный алгоритм), — если установить его в положение Yes (Да), позволяет использовать модификацию численного метода для решения уравнений, определяемых не обязательно гладкими функциями. Как мы убедились в этом разделе, все градиентные методы, реализованные в функции Find, требуют многократного вычисления производных. Если вы работаете с достаточно гладкими функциями, то градиентные методы обеспечивают быстрый и надежный поиск корня. Для поиска корня недостаточно гладких функций одной переменной следует либо выставить данную опцию функции Find, либо использовать метод секущих (функцию root). Помните, что правильный выбор численного метода и его параметров может помочь при решении нестандартной задачи, которая при стандартных установках может и не поддаваться решению.
Графическая иллюстрация решения кубического уравнения
Рисунок 5.4. Графическая иллюстрация решения кубического уравнения

Как уже отмечалось выше, результатом численного решения алгебраического уравнения является один его корень. Для того чтобы отыскать остальные корни, необходимо повторно решить уравнение, взяв для переменной х другие начальные значения. Например, если присвоить ей в начале листинга значение х=-1, то численным процессором будет выдан в качестве результата другой корень х=0 (листинг 5.9). Такая работа программы Mathcad связана с особенностями применяемых численных алгоритмов (см. разд. 5.3). Для численного определения всех корней уравнения следует применять специальные приемы, например, сканирование по неизвестным (см. разд. 5.2.4).
Графическая интерпретация решения
Рисунок 5.2. Графическая интерпретация решения системы двух уравнений (см. листинг 5.7)

График функции f (х) =3х3+2х27х
Рисунок 5.1. График функции f (х) =3х3+2х2-7х

В листинге 5.1 вы видите все три последовательные строки вычислительного блока. Первая строка представляет собой обязательное ключевое слово Given, следующая строка является, собственно, записью уравнения (5.3), а в последней строке листинга включается в работу встроенная функция Find. Обратите внимание, что после имени функции Find находится оператор символьного вывода, справа от которого (по истечении необходимого времени работы символьного процессора) возникает аналитический результат решения уравнения. Существенно, что он является точным решением (записанным в данном случае в трансцендентном виде), а получить числовые значения корней можно, поставив после него символ численного равенства (как это сделано в последней строке листинга 5.1).
Как видно из листинга 5.1, уравнение имеет три различных корня, которые представляются справа от функции соответствующим трехкомпонентным вектором. Таким образом, решение предлагается пользователю в форме матрицы размера 1хз (одна неизвестная переменная имеет три значения, каждое из которых обращает уравнение в тождество).
Пример, использованный в листинге 5.1, включает уравнение, записанное в традиционной форме равенства. Приведем решение того же самого уравнения, если оно представлено в несколько другой форме, подчеркивающей специфику задачи нахождения корней функции (листинг 5.2). Основное отличие листинга 5.2 от предыдущего связано с другой формой записи исследуемого уравнения через функцию пользователя f (x). Иными словами, подчеркивается специфика поставленной задачи отыскания нулевых значений некоторой функции.
Важно заметить, что точное решение уравнения (непосредственно после оператора символьного вывода результата работы функции Find) обращает f (х) в тождественный ноль, а пересчитанные числовые значения корней (после знака обычного равенства) обеспечивают лишь ее приближенное равенство нулю (разумеется, это связано с ошибками округления).
ВНИМАНИЕ!
Не забывайте о том, что вводить знаки равенства в уравнение в пределах вычислительного блока Given/Find следует при помощи панели Boolean (Булевы операторы).
График функции ln(ах2)=х (для а=3 и а=30)
Рисунок 5.11. График функции ln(ах2)=х (для а=3 и а=30)

Иллюстрация метода Ньютона
Рисунок 5.8. Иллюстрация метода Ньютона

Модификация алгоритма Ньютона для решения системы нескольких уравнений заключается в линеаризации соответствующих функций многих переменных, т. е. аппроксимации их линейной зависимостью с помощью частных производных.
Например, для нулевой итерации в случае системы двух уравнений используются выражения типа:

Чтобы отыскать точку, соответствующую каждой новой итерации, требуется приравнять оба равенства нулю, т. е. решить на каждом шаге полученную систему линейных уравнений.
Выбор градиентного алгоритма
Как уже отмечалось, Mathcad предлагает три различных варианта градиентных методов. Чтобы поменять численный метод:
1. Щелкните правой кнопкой мыши на названии функции Find.
2. Наведите указатель мыши на пункт Nonlinear (Нелинейный) в контекстном меню.
3. В появившемся подменю (Рисунок 5.9) выберите один из трех методов: Conjugate Gradient (Сопряженных градиентов), Quasi-Newton (квазиньютоновский) или Levenberg-Marquardt (Левенберга—Маркарда).
Иллюстрация метода секущих
Рисунок 5.7. Иллюстрация метода секущих

Результат, показанный на Рисунок 5.7, получен для погрешности вычислений, которой в целях иллюстративности предварительно присвоено значение TOL=0.5. Поэтому для поиска корня с такой невысокой точностью оказалось достаточно одной итерации. В вычислениях, приведенных в листингах 5.13— 5.15 (см. разд. 5.2.2), погрешность TOL=0.001была установлена по умолчанию, и решение, выданное численным методом, лежало намного ближе к истинному положению корня. Иными словами, чем меньше константа TOL, тем ближе к нулю будет значение f (х) в найденном корне, но тем больше времени будет затрачено вычислительным процессором Mathcad на его поиск.
Примечание 1
Примечание 1
Соответствующий пример можно найти на компакт-диске, а также в Быстрых шпаргалках. Он расположен в разделе "Solving Equations" (Решение уравнений) и называется "Effects of TOL on Solving Equations" (Влияние константы TOL на решение уравнений).
Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в области локального максимума или минимума f (х). В этом случае секущая может иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого положения корня. Для решения таких уравнений лучше применять другую встроенную функцию Minerr (см. разд. 6.2). Аналогичные проблемы могут возникнуть, если начальное приближение выбрано слишком далеко от настоящего решения или f (х) имеет особенности типа бесконечности.
Аналитическое решение кубического уравнения
Листинг 5.1. Аналитическое решение кубического уравнения

Аналитический поиск нулей функции f(x)
Листинг 5.2. Аналитический поиск нулей функции f(x)

В заключение разговора о символьном решении уравнений с одним неизвестным приведем еще два показательных примера, связанных с нахождением нулей функции нескольких аргументов (т. е. зависящих, помимо, собственно, неизвестного, еще и от дополнительных параметров).
демонстрирует как
Листинг 5.3 демонстрирует, как выглядит решение уравнения, включающего четыре различные переменные, по некоторым из этих переменных. Обратите внимание на последний из трех приведенных в листинге 5.3 примеров, иллюстрирующий результат решения уравнения относительно сразу всех входящих в него параметров.
Помните, что для корректной работы символьного процессора вовсе не обязательно задавать конкретные значения переменных, входящих в уравнение, а если такие значения (для некоторых, либо всех, параметров) определены, то это учитывается при выводе результата (что иллюстрируется листингом 5.4).
Символьное решение
Листинг 5.3. Символьное решение уравнения относительно разных переменных

Символьное решение
Листинг 5.4.Символьное решение уравнения, зависящего от параметров, в случае предварительного задания их числовых значений

Если решить уравнение аналитически не удается, то результатом применения оператора символьного вывода после функции Find будет либо тривиальное выражение типа Find(x)->
x (как в листинге 5.5), либо сообщение об ошибке "No symbolic result was found" (Ни один символьный результат не найден). Следует помнить, что символьный процессор Mathcad "умеет" находить не только действительные, но и комплексные корни уравнений. В качестве примера приведем листинг 5.6 с решением кубического уравнения, имеющего три очевидных корня — одного действительного (равного нулю) и двух чисто мнимых (±i, где i — мнимая единица).
Решить уравнение аналитически не удается
Листинг 5.5. Решить уравнение аналитически не удается

Символьное решение
Листинг 5.6. Символьное решение уравнения, имеющего и действительные, и мнимые корни
="10.gif" >
Символьное решение системы двух уравнений
Листинг 5.7. Символьное решение системы двух уравнений

Численное решение
Листинг 5.8. Численное решение кубического уравнения с начальным значением x=1

Численное решение
Листинг 5.9. Численное решение кубического уравнения с начальным значением x=-1 сходится к другому корню x=0

Системы уравнений
Приведем еще один пример численного решения алгебраических уравнений, обратившись на этот раз к системе двух уравнений, которая также уже исследовалась нами при помощи символьного процессора. Система имеет два решения, показанные графически на Рисунок 5.2 и найденные аналитически в листинге 5.7 (см. разд 5.1.3).
Численное решение
Листинг 5.10. Численное решение системы алгебраических уравнений

Если предпринять попытку решить несовместную систему, в частности, в рассматриваемом примере добавить еще одно уравнение, то Mathcad выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.
Особую осторожность следует соблюдать при решении систем с числом неизвестных большим, чем число уравнений. Например, можно удалить одно из двух уравнений из рассмотренной нами задачи, попытавшись решить оставшееся единственное уравнение с двумя неизвестными х и у (листинг 5.11). В такой постановке задача имеет бесконечное множество корней: для любого х и, соответственно, у=х2-1 условие, определяющее единственное уравнение, выполнено. Однако даже если корней бесконечно много, численный метод будет производить расчеты только до тех пор, пока логические выражения в вычислительном блоке не будут выполнены (конечно, в пределах погрешности). После этого итерации будут остановлены и выдано решение. В результате будет найдена всего одна пара значений (х,у), обнаруженная первой, как это показано в последней строке листинга 5.11.
Примечание 6
Примечание 6
Для того чтобы найти все решения рассматриваемой задачи, можно обратиться к возможностям символьного процессора Mathcad. Достаточно в последней строке листинга заменить знак равенства на оператор символьного вывода, и в качестве ответа будет выдано семейство решений х и х2-1.
демонстрирующий численное
Листинг 5.10, демонстрирующий численное решение рассматриваемой системы, начинается с присвоения неизвестным начальных значений х=10,у=10. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. В результате (последняя строка листинга) Mathcad находит один из корней х=1,у=0, причем первый элемент вектора решения есть первый аргумент функции Find, а второй элемент — ее второй аргумент. Поскольку решение производится численным методом, оно выдается с некоторой погрешностью, не превышающей встроенной константы CTOL. Если задать в первой строке листинга другие начальные значения, расположенные ближе к другому корню, например, х=0,у=0, то найден в итоге будет другой корень х=-0.5,у=-0.75.
Примечание 4
Примечание 4
На самом деле в вычислительном блоке используются обе системные константы Mathcad, связанные с заданием погрешности: TOL и CTOL. Константа CTOL ограничивает невязку, т. е. задает точность выполнения уравнений, введенных после ключевого слова Given. Например, если CTOL=0.001, то уравнение х=10 будет считаться выполненным и при х=10.001, и при х=9.999. Другая константа TOL определяет условие прекращения итераций численным алгоритмом (см. разд. 5.4). Значение CTOL может быть задано пользователем так же, как и TOL, например, CTOL=0.01. По умолчанию принято, что CTOL= =TOL=0.001, но вы по желанию можете переопределить их.
Примечание 5
Примечание 5
Часто бывает очень полезным проверить точность решения уравнений "вручную", подставив найденные вычислительным процессором корни в исходные уравнения и оценив значение их невязок.
Численное решение
Листинг 5.11. Численное решение уравнения, имеющего бесконечное множество корней, приводит к одному из них
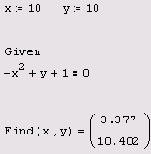
Системы уравнений и неравенств
Пока мы рассматривали примеры систем уравнений, число которых было таким же, как и число неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х в рассмотренный выше листинг 5.10 приведет к нахождению другого решения, как это показано в листинге 5.12.
Обратите внимание, что, несмотря на те же начальные значения, что и в листинге 5.10, в листинге 5.12 мы получили другой корень системы уравнений. Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке листинга 5. 12.
Численное решение
Листинг 5.12. Численное решение системы алгебраических уравнений и неравенств

Два варианта уравнения методом секущих
Листинг 5.13. Два варианта уравнения методом секущих

Как вы можете убедиться (первая строка листинга 5.13), для решения уравнения при помощи функции root (f (x) ,x,a,b) не требуется задавать начального приближения, а достаточно указать интервал [а,b]. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Когда root имеет четыре аргумента, следует помнить о двух ее особенностях. Во-первых, внутри интервала не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно. Во-вторых, значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.
В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были "хорошими", т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.
Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на Рисунок 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.
Пример уравнения
Листинг 5.14. Пример уравнения, которое удается решить только методом секущих
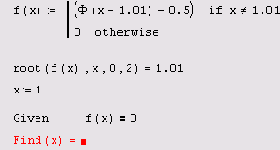
Поиск корней уравнения
Листинг 5.15. Поиск корней уравнения, зависящего от двух переменных

Вычисление корней полинома
Листинг 5.16. Вычисление корней полинома

Обратим внимание на результат применения функции polyroots, заметив, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.
Для функции polyroots можно выбрать один из двух численных методов — метод полиномов Лаггера (он установлен по умолчанию) или метод парной матрицы.
Для смены метода:
1. Вызовите контекстное меню, щелкнув правой кнопкой мыши на слове polyroots.
2. В верхней части контекстного меню выберите либо пункт LaGuerre (Лаггера), либо Companion Matrix (Парная матрица).
3. Щелкните правой кнопкой мыши вне действия функции polyroots — если включен режим автоматических вычислений, будет произведен пересчет корней полинома в соответствии с вновь выбранным методом.
Для того чтобы оставить за Mathcad выбор метода решения, установите флажок AutoSelect (Автоматический выбор), выбрав одноименный пункт в том же самом контекстном меню.
Попытка отыскания
Листинг 5.17.Попытка отыскания зависимости x(a) решения уравнения ln(ax2)=x

Поиск зависимости
Листинг 5.18. Поиск зависимости x(a) решения уравнения ln(ax2)=x методом продолжения

Модельная функция f (х) (продолжение листинга 5 14)
Рисунок 5.5. Модельная функция f (х) (продолжение листинга 5.14)

Остается добавить, что f (х) может быть функцией не только х, а любого количества аргументов. Именно поэтому в самой функции root необходимо определить, относительно какого из аргументов следует решить уравнение. Эта возможность проиллюстрирована листингом 5.15 на примере функции двух переменных f (x,y)=x2-y2+1. В нем сначала решается уравнение f (х, 0) =0 относительно переменной х, а потом — другое уравнение f (0, у) =0 относительно переменной у, причем, благодаря удачному подбору начальных значений, вычисляются все корни данного квадратичного уравнения.
Таким образом, в обоих случаях один из аргументов функции f (х) воспринимается как неизвестное, а другой — как параметр. Не забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки "This variable or function is not defined above", в данном случае говорящей о том, что другая переменная ранее не определена.
Примечание 1
Примечание 1
Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 5.3.3.
Нелинейные алгебраические уравнения
Нелинейные алгебраические уравнения
Огромное количество задач вычислительной математики связано с решением нелинейных алгебраических уравнений, а также систем таких уравнений. При этом необходимость решения нелинейных уравнений возникает зачастую на промежуточных шагах, при реализации фрагментов более сложных алгоритмов (к примеру, при расчетах дифференциальных уравнений при помощи разностных схем и т. п.).
Постановка задач выглядит следующим образом. Пусть имеется либо одно алгебраическое уравнение с неизвестным х: f(x)=0, (где f(х) — некоторая функция), либо система из N алгебраических уравнений:

Требуется найти корни, т. е. все значения х (или, в случае системы все м-покомпонентные векторы х), которые переводят уравнение (или, соответственно, систему уравнений) в верное равенство (равенства).
Примечание 1
Примечание 1
Решение систем линейных уравнений, у которых все функции имеют вид fi (х)=аi1х1+аi2х2+. . . +ainxN, представляет собой отдельную задачу вычислительной линейной алгебры. Она рассматривается в главе 8.
О численных методах
5.3. О численных методах
Уделим теперь небольшое внимание численным алгоритмам, которые используются в работе встроенных функций Find и root, чтобы читатель имел возможность применять их для решения алгебраических уравнений более осмысленно.
Поиск зависимости х (а) решения
Рисунок 5.13. Поиск зависимости х (а) решения уравнения ln(ах2) =х методом продолжения (продолжение листинга 5.18)

Результаты вычислений, приведенные в виде двух графиков на Рисунок 5.13, разительно отличаются от предыдущего. Как видно, столь малое изменение идеологии применения численного метода привело к определению непрерывного семейства корней. Отметим, что получить результат Рисунок 5.12 (без продолжения по параметру) в терминах введенной нами в листинге 5.18 функции f(x0,a) можно, изменив ее первый аргумент на константу: f (1,ai).
Примечание 1
Примечание 1
С помощью метода продолжения можно решать и соответствующие задачи оптимизации, зависящие от параметра. Идеология в этом случае остается точно такой же, но вместо функций решения нелинейных уравнений root или Find вам следует применить одну из функций поиска экстремума Minerr, Maximize или Minimize (СМ. разд. 6.1 и 6.2).
Мы привели основную идею и один из возможных способов реализации метода продолжения по параметру. Безусловно, вы можете предложить иные, как математические, так и программистские решения этой проблемы. В частности, для выбора очередного начального приближения к корню можно использовать результат экстраполяции уже найденной зависимости х (а), придумать более сложные алгоритмы для ветвящихся семейств решений и т.д.
Попытка отыскания зависимости
Рисунок 5.12. Попытка отыскания зависимости х (а) решения уравнения ln(ах2)=х (продолжение листинга 5.17)
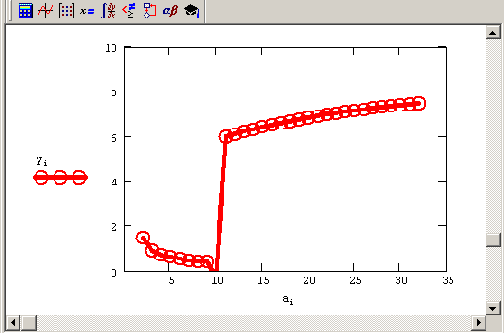
Решим данное уравнение методом секущих, применяя для этого встроенную функцию root. Самый простой, но далеко не лучший, способ иллюстрируется листингом 5.17. Начинается листинг с вывода графика функции ln(ах2)=х, корни которой нам предстоит исследовать (ради определенности, для положительных значений х). Глядя на график, сразу можно сказать, что на рассматриваемом интервале уравнение будет иметь два решения (для каждого значения параметра а, больших некоторого порогового значения, ниже которого, видимо, уравнение вовсе не имеет корня).
Для того чтобы получить зависимость решения уравнения от параметра а, в следующих строках листинга создается ранжированная переменная i, с помощью которой определяется вектор значений параметра ai. Его элементы пробегают значения от 3 до 33 с шагом 1(эти числа взяты ради примера, вы можете поэкспериментировать с другими значениями и убедиться в том, что для значений параметра ниже порога а=3 решение уравнения отсутствует).
Последняя строка листинга присваивает элементам еще одного вектора у вычисленные с помощью функции root значения корней уравнения для каждого ai. Но для того чтобы функция root заработала, необходимо предварительно задать начальное приближение к решению, что сделано в предыдущей строке. Ключевой момент метода, примененного в листинге 5.17, заключается в том, что одно и то же начальное значение х=1 использовано для решения уравнения при всех ai.
Результат расчетов yi показан на Рисунок 5.12. Обратите внимание, что по мере увеличения а кривая корней уравнения сначала плавно идет по одному (нижнему) семейству решений, а потом (в районе а=и) явно срывается, "перепрыгивая" на другое семейство. С вычислительной точки зрения такая ситуация чаще всего крайне неблагоприятна, поскольку хотелось бы отыскать непрерывное семейство решений. Скачки зависимости у (а) могут вводить пользователя в заблуждение, вовсе скрывая от него существование нижнего семейства решений при а>п.
Почему же происходят эти скачки с одного семейства решений на другое? Конечно, причина кроется в выборе начального значения для вычисления каждого из корней. Линия начальных значений х=1 обозначена на графике функции (Рисунок 5.11) в виде пунктирной вертикальной прямой. Для а0=3, и вообще для нескольких первых а0 начальное значение х=1 находится ближе всего к нижнему семейству решений. Поэтому неудивительно, что численный метод находит именно эти корни. В правой части графика к линии начальных значений ближе второе (верхнее) семейство решений, к ним-то и приводит численный метод.
Приведенные соображения диктуют очень простой рецепт избавления от скачков и нахождения одного из семейств непрерывных решений. Для этого требуется при поиске каждого (i+1)-го корня взять начальное значение, по возможности близкое к отыскиваемому семейству. Неплохим вариантом будет выбор приближения в виде предыдущего 1-го корня, который был найден для прошлого значения параметра а0 Возможный вариант воплощения этого метода, называемого продолжением по параметру, Приведен в листинге 5.18. В нем функция root применена внутри функции пользователя f(x0,a), определенной в самом начале листинга с помощью средств программирования. Назначение функции f (х0,а) заключается в том, что она выдает значение корня для заданного значения параметра а и начального приближения к решению хо. В остальном смысл листинга повторяет предыдущий, за исключением того, что осуществляется поиск сразу обоих семейств решений у и z, причем для каждого сначала явно задается начальное значение только для точки а0. Для всех последующих точек, как следует из последней строки листинга, взято начальное значение, равное предыдущему корню.
Символьное решение уравнений
5.1. Символьное решение уравнений
Относительно небольшое количество задач отыскания корней алгебраических уравнений можно решить аналитически, а на практике почти всегда приходится искать решение при помощи численных методов. Тем не менее мы начнем знакомство с принципами решения алгебраических уравнений в Mathcad именно с описания использования символьного процессора, что позволит, с одной стороны, освоить соответствующий инструментарий Mathcad, а с другой — лучше понять специфику исследуемых задач.
Символьное решение уравнения
Рисунок 5.3. Символьное решение уравнения

В итоге после выражения появится строка с результатом решения уравнения (т. е. значениями переменной, которые обращают исходное выражение в ноль). Следует иметь в виду, что решение уравнения производится именно по той переменной, которую пользователь выделяет перед вводом команды меню. Разумеется, если выделять различные переменные, то в итоге будут выдаваться совершенно разные решения.
ВНИМАНИЕ!
Помните о том, что символьные вычисления, проводимые при помощи меню, не являются "живыми", т. е. не будут меняться впоследствии, если вы будете редактировать исходное выражение.
Сканирование по переменной х
Рисунок 5.6. Сканирование по переменной х

Выбор численного алгоритма
Рисунок 5.9. Выбор численного алгоритма

Чтобы вернуть автоматический выбор типа численного метода, в контекстном меню надо выбрать пункт AutoSelect (Автоматический выбор). Если установлена опция автоматического выбора (о чем говорит флажок, установленный в пункте AutoSelect), то текущий тип численного метода можно узнать, вызвав то же самое подменю и посмотрев, который из них отмечен точкой. Два последних метода являются квази-ньютоновскими, основная идея которых была рассмотрена выше. Первый из них, метод сопряженных градиентов, является двухшаговым — для поиска очередной итерации он использует как текущую, так и предыдущую итерации. Алгоритм Левенберга подробно описан в справочной системе Mathcad, а подробную информацию о методах Ньютона и сопряженных градиентов можно найти в большинстве книг по численным методам.
Параметры градиентных алгоритмов
Помимо выбора самих методов имеется возможность устанавливать их некоторые параметры. Для этого нужно вызвать с помощью того же контекстного меню диалоговое окно Advanced Options (Дополнительные параметры), выбрав в контекстном меню пункты Nonlinear / Advanced options (Нелинейный / Дополнительные параметры). В этом диалоговом окне (Рисунок 5.10) имеется пять групп переключателей по два в каждой.
В первой строке — Derivative estimation (Аппроксимация производной) — определяется метод вычисления производной Forward (Вперед) или Central (Центральная). Они соответствуют аппроксимации производной либо правой (двухточечная схема "вперед"), либо центральной (трехточечная симметричная схема) конечной разностью.
Примечание 1
Примечание 1
Обратите внимание, что вычисление производной в градиентных численных методах решения уравнений производится более экономичным способом, нежели при численном дифференцировании (см. главу 3).