Автоматическая генерация матриц
7.4.1. Автоматическая генерация матриц
Самым наглядным способом создания матрицы или вектора является применение первой кнопки панели инструментов Matrix (Матрицы). Однако в большинстве случаев, в частности, при программировании сложных проектов, удобнее бывает создавать массивы с помощью встроенных функций.
Создание матриц на основе некоторой функции
Наиболее удобный прием автоматизации создания матриц заключается в предварительном определении функции f (i, j), аргументом которой должны быть индексы элементов матрицы:
matrix (м, N, f) — создание матрицы размера MхN, каждый i,j элемент которой есть f (i, j) (листинг 7.20):
M — количество строк матрицы; N — количество столбцов матрицы; f(i,j) —функция.
Модуль вектора
7.2.1. Модуль вектора
Модуль вектора (vector magnitude) по определению равен квадратному корню из суммы квадратов его элементов (листинг 7.8).
ВНИМАНИЕ!
Не путайте модуль вектора и определитель матрицы, который обозначается тем же символом (с/м. разд. 7,3.1). Это характерный пример оператора, действующего по-разному на векторы и квадратные матрицы.
Определитель квадратной матрицы
7.3.1. Определитель квадратной матрицы
Определитель (Determinant) матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinant (Определитель) на панели инструментов Matrix (Матрица) (листинг 7.14) или набрать на клавиатуре <|> (нажав клавиши <Shift>+<\>). В результате любого из этих действий появляется местозаполнитель, в который следует поместить матрицу. Чтобы вычислить определитель уже введенной матрицы:
1. Переместите курсор в документе таким образом, чтобы поместить матрицу между линиями ввода (напоминаем, что линии ввода — это вертикальный и горизонтальный отрезки синего цвета, образующие уголок, указывающий на текущую область редактирования).
2. Введите оператор нахождения определителя матрицы.
3. Введите знак равенства (либо символьного вывода), чтобы вычислить определитель (численно или аналитически соответственно, как это показано в листинге 7.14).
ВНИМАНИЕ!
Не путайте операторы вычисления определителя квадратной матрицы и длины вектора. В Matncad 12 введен принудительный контроль действий пользователя при вводе этих операторов во избежание путаницы (т. к. один и тот же символ используется для этих двух операций). При попытке вычислить определитель матрицы с помощью оператора |А|, введенного с панели Calculator (Калькулятор), а не Matrix (Матрица), будет выдано сообщение об ошибке, а результат вычисления детерминанта появится только после того, как пользователь вызовет контекстное меню и подтвердит в нем, что он собирается вычислить именно определитель матрицы. То же самое касается и длины вектора, если попытаться ввести его не с панели Calculator (Калькулятор), а с панели Matrix (Матрица).
Транспонирование
7.1.1. Транспонирование
Транспонированием называют операцию, переводящую матрицу размерности MxN в матрицу размерности NxM, делая столбцы исходной матрицы строками, а строки — столбцами. Несколько примеров транспонирования приведены в листинге 7.1. Ввод символа транспонирования (transpose) осуществляется с помощью панели инструментов Matrix (Матрица) или нажатием клавиш <Ctrl>+<!>. He забывайте, что для вставки символа транспонирования матрица должна находиться между линиями ввода.
Ранг матрицы
7.3.2. Ранг матрицы
Рангом (rank) матрицы называют наибольшее натуральное число к, для которого существует не равный нулю определитель k-ro порядка подматрицы, составленной из любого пересечения k столбцов и k строк матрицы.
Для вычисления ранга в Mathcad предназначена функция rank (листинг 7.15).
rank (A) — ранг матрицы:
А — матрица.
Разбиение и слияние матриц
7.4.2. Разбиение и слияние матриц
Из матрицы или вектора можно выделить либо подматрицу, либо вектор-столбец, либо отдельный элемент. И обратно, можно "склеить" несколько матриц в одну.
Выделение подматрицы
Часть матрицы выделяется одним из следующих способов (листинг 7.22):
для выделения одного элемента предназначен оператор нижнего индекса. Оператор вводится нажатием кнопки Subscript (Нижний индекс) со значком хn„ на панели Matrix (Матрица), либо нажатием клавиши <[> (вторая строка листинга 7.22); для выделения из матрицы столбца примените оператор выделения столбца нажатием кнопки Matrix Column с изображением угловых скобок <> на панели Matrix, либо сочетанием клавиш <Ctrl>+<6> (третья строка листинга 7.22). Этот оператор называют еще, по аналогии с предыдущим, оператором верхнего индекса; чтобы выделить из матрицы строку, примените тот же оператор <> к транспонированной матрице (конец листинга 7.22); для выделения подматрицы используйте встроенную функцию submatrix (A, ir, jr, ic, jc), возвращающую часть матрицы А, находящуюся между строками ir,jr и столбцами ic,jc включительно (листинг 7.23).
Скалярное произведение
7.2.2. Скалярное произведение
Скалярное произведение векторов (vector inner product) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов u и v равно uv=|u||v|cos0, где 0— угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение (листинг 7.9).
ВНИМАНИЕ!
Для обозначения скалярного произведения пользователю позволяется выбирать представление оператора умножения при помощи контекстного меню (подобно умножению скалярных величин). Однако никогда не применяйте для обозначения скалярного произведения символ х, который является общеупотребительным символом векторного произведения (см. разд. 7.2.3).
Сложение и вычитание
7.1.2. Сложение и вычитание
В Mathcad можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются стандартные символы "+" или "—" соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых (листинг 7.2).
Результат унарной операции смены знака матрицы эквивалентен смене знака всех ее элементов. Для того чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом (нижняя строка листинга 7.2).
Обращение квадратной матрицы
7.3.3. Обращение квадратной матрицы
Поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку Inverse (Обратная матрица) на панели инструментов Matrix (Матрица). В листинге 7.16 приведен пример поиска обратной матрицы и последующая проверка правильности ее вычисления.
Сортировка элементов матриц
7.4.3. Сортировка элементов матриц
Часто бывает нужно переставить элементы матрицы или вектора, расположив их в определенной строке или столбце в порядке возрастания или убывания. Для этого имеются несколько встроенных функций, которые позволяют гибко управлять сортировкой матриц:
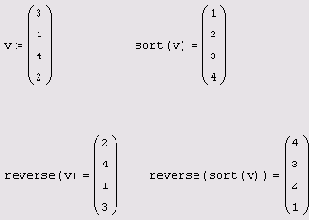
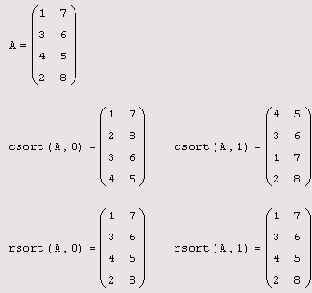
sort(v) — сортировка элементов вектора в порядке возрастания (листинг 7.26, верхняя строка); reverse (v) — перестановка элементов вектора в обратном порядке (листинг 7.26, нижняя строка); csort (A, i) — сортировка строк матрицы выстраиванием элементов 1-го столбца в порядке возрастания (листинг 7.27, верхняя строка); rsort (A, i) — сортировка столбцов матрицы выстраиванием элементов i-й строки в порядке возрастания (листинг 7.27, нижняя строка):
v — вектор; А — матрица; i — индекс строки или столбца.
Примечание 1
Примечание 1
Если элементы матриц или векторов комплексные, то сортировка ведется по действительной части, а мнимая часть игнорируется.
Умножение
7.1.3. Умножение
При умножении следует помнить, что матрицу размерности MxN допустимо умножать только на матрицу размерности NxP (р может быть любым). В результате получается матрица размерности MхP.
Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение). Умножение матриц обозначается по умолчанию точкой, как показано в листинге 7.5.
Векторное произведение
7.2.3. Векторное произведение
Векторное произведение (cross product) двух векторов u и v с углом 9 между ними равно вектору с модулем |u|-|v|sin0, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом х, который можно ввести нажатием кнопки Cross Product (Векторное произведение) в панели Matrix (Матрица) или сочетанием клавиш <Ctrl>+<8>. Пример приведен в листинге 7.11.
Векторизация массива
7.2.4. Векторизация массива
Векторная алгебра Mathcad включает несколько необычный оператор, который называется оператором векторизации (vectorize operator). Этот оператор предназначен, как правило, для работы с массивами. Он позволяет провести однотипную операцию над всеми элементами массива (т. е. матрицы или вектора), упрощая тем самым программирование циклов. Например, иногда требуется умножить каждый элемент одного вектора на соответствующий элемент другого вектора, чтобы в результате также получился вектор. Непосредственно такой операции в Mathcad нет, но ее легко осуществить с помощью векторизации (листинг 7.12). Для этого:
1. Введите векторное выражение, как показано во второй строчке листинга 7.12 (обратите внимание, что в таком виде символ умножения обозначает оператор скалярного произведения векторов).
2. Переместите курсор таким образом, чтобы линии ввода выделяли все выражение, которое требуется подвергнуть векторизации.
3. Введите оператор векторизации, нажав кнопку Vectorize (Векторизация) на панели Matrix (Матрица) (листинг 7.12), или сочетанием клавиш <Ctrl>+<->.
4. Введите <=>, чтобы получить результат.
Возведение квадратной матрицы в степень
7.3.4. Возведение квадратной матрицы в степень
К квадратным матрицам можно формально применять операцию возведения в степень п. Для этого n должно быть целым числом. Результат данной операции приведен в табл. 7.1. Ввести оператор возведения матрицы м в степень n можно точно так же, как и для скалярной величины: нажав кнопку Raise to Power (Возвести в степень) на панели Calculator (Калькулятор) или нажав клавишу <А>. После появления местозаполнителя в него следует ввести значение степени n.
Таблица 7.1. Правила возведения матрицы в степень
| n |
Мn |
| 0 |
Единичная матрица размерности матрицы M |
| 1 |
Сама матрица M |
| -1 |
M-1 — матрица, обратная M |
| 2,3,... |
MM, (MM)M, . . . |
| -2, -3, ... |
M-1M-1, (M-1M-1)M-1 ... |
Примеры возведения матрицы в степень приведены в листинге 7.17.
Вывод размера матрицы
7.4.4. Вывод размера матрицы
Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции (листинги 7.28 и 7.29 соответственно):
rows (A) — число строк; cols (А) — число столбцов; length (v) — число элементов вектора; last (v) — индекс последнего элемента вектора:
А — матрица или вектор; v — вектор.
Примечание 1
Примечание 1
Если матричные индексы нумеруются с 1, т. е. системная константа ORIGIN равна не о (по умолчанию), а 1, то число элементов вектора и индекс его последнего элемента совпадают.
Матричные нормы
7.3.5. Матричные нормы
В линейной алгебре используются различные векторные и матричные нормы (norm), которые ставят в соответствие матрице некоторую скалярную числовую характеристику. Норма матрицы отражает порядок величины матричных элементов. В разных специфических задачах линейной алгебры применяются различные виды норм. Mathcad имеет четыре встроенных функции для расчета разных норм квадратных матриц:
norm1 (A) — норма в пространстве L1; norm2 (A) — норма в пространстве L2; norme (A) — евклидова норма (euclidean norm); normi (A) — max-норма, или ?-норма (infinity norm):
А — квадратная матрица.
Примеры расчета различных норм двух матриц А и в с различающимися на два порядка элементами иллюстрирует листинг 7.18.
СОВЕТ
В большинстве задач неважно, какую норму использовать. Как видно, в обычных случаях разные нормы дают примерно одинаковые значения, хорошо отражая порядок величины матричных элементов. Конкретные формулы, определяющие нормы, заинтересованный читатель отыщет в справочниках по линейной алгебре или в Ресурсах Mathcad.
Число обусловленности квадратной матрицы
7.3.6. Число обусловленности квадратной матрицы
Еще одной важной характеристикой матрицы является ее число обусловленности (condition number). Число обусловленности является мерой чувствительности системы линейных уравнений А-Х=Ь, определяемой матрицей А, к погрешностям задания вектора ь правых частей уравнений (см. главу 8). Чем больше число обусловленности, тем сильнее это воздействие и тем более неустойчив процесс нахождения решения линейной системы. Число обусловленности связано с нормой матрицы и вычисляется по-разному для каждой из норм:
cond1 (А) — число обусловленности в норме L1; cond2 (A) — число обусловленности в норме L2; conde (A) — число обусловленности в евклидовой норме; condi (A) — число обусловленности в ?-норме:
А — квадратная матрица.
Расчет чисел обусловленности для двух матриц А и В показан в листинге 7.19. Обратите внимание, что первая из матриц является хорошо обусловленной, а вторая — плохо обусловленной (два ее последних столбца очень близки между собой, с точностью до множителя 2). Вторая строка листинга дает формальное определение числа обусловленности как произведения норм исходной и обратной матриц. В других нормах определение точно такое же.
Примечание 1
Примечание 1
Как нетрудно понять, матрицы А и в из листинга 7.18 (см. предыдущий разд.) обладают одинаковыми числами обусловленности, т. к. в=100-А, и, следовательно, обе матрицы определяют одну и ту же систему уравнений.
Использование функции CreateMesh
Рисунок 7.3. Использование функции CreateMesh для построения графика трехмерной поверхности

Результатом обеих рассмотренных функций CreateMesh и CreateSpace является соответствующий вложенный массив, служащий в Mathcad для представления тензора. Каждая матрица из числа трех вложенных матриц, образующих вложенный массив данных, определяет х-, у- и z-координаты точек поверхности или кривой.
Создание диагональных матриц
В Mathcad легко создать матрицы, имеющие определенное простое строение, с помощью одной из встроенных функций. Примеры использования этих функций приведены в листинге 7.21:
identity (N) — единичная матрица размера NxN; diag(v) — диагональная матрица, на диагонали которой находятся элементы вектора v:
N — целое число; v — вектор.
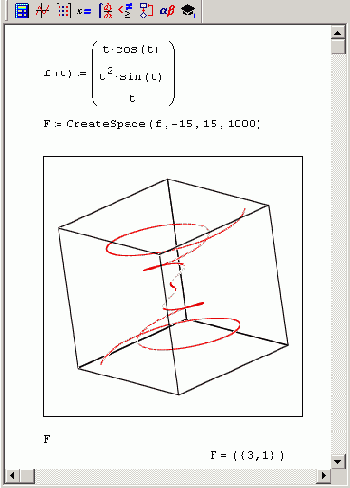
Использование функции CreateSpace
Рисунок 7.2. Использование функции CreateSpace для построения графика трехмерной кривой
Функция создания матрицы для графика трехмерной поверхности устроена совершенно аналогично, за тем исключением, что для определения поверхности требуется не одна, а две переменных. Пример ее использования иллюстрирует Рисунок 7.3.
CreateMesh(F(или g, или f1,f2,f3),s0,s1,t0,t1,sgrid,tgrid, fmap) — создание вложенного массива, представляющего х-, у- и z-координаты параметрической поверхности, заданной функцией F:
F(s,t) — векторная функция из трех элементов, заданная параметрически относительно двух аргументов s и t; g (s, t) — скалярная функция; f1(s,t) ,f2 (s,t) ,f3(s,t) — скалярные функции; s0, t0 — нижние пределы аргументов s, t (по умолчанию -5); s1,t1 — верхние пределы аргументов s,t (по умолчанию 5); sgrid, tgrid — число точек сетки по переменным s и t (по умолчанию 20); fmap — векторная функция из трех элементов от трех аргументов, задающая преобразование координат.
Линейная алгебра
Линейная алгебра
Задачи линейной алгебры, решаемые в Mathcad, можно условно разделить на два класса. Первый — это простейшие матричные операции, которые сводятся к определенным арифметическим действиям над элементами матрицы. Они реализованы в виде операторов (см. разд. 7.1 и 7.2) и нескольких специфических функций, предназначенных для создания, объединения, сортировки, получения основных свойств матриц и т. п. (см. разд. 7.4). Второй класс — это более сложные действия, которые реализуют алгоритмы вычислительной линейной алгебры, такие как вычисление определителей и обращение матриц (см. разд. 7.3), вычисление собственных векторов и собственных значений, решение систем линейных алгебраических уравнений и различные матричные разложения (см. главу 8).
Транспонирование векторов и матриц
Листинг 7.1. Транспонирование векторов и матриц

Сложение вычитание и смена знака матриц
Листинг 7.2. Сложение, вычитание и смена знака матриц
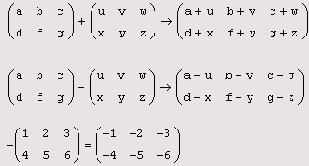
Кроме сложения матриц Mathcad поддерживает операцию сложения матрицы со скаляром (листинг 7.3). Каждый элемент результирующей матрицы равен сумме соответствующего элемента исходной матрицы и скалярной величины.
Сложение матрицы со скалярной величиной
Листинг 7.3. Сложение матрицы со скалярной величиной
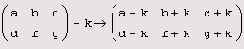
Иногда бывает нужно вычислить сумму всех элементов вектора или матрицы. Для этого существует вспомогательный оператор (листинг 7.4, первая и вторая строки соответственно), задаваемый кнопкой Vector Sum (Суммирование элементов вектора) на панели Matrix (Матрица) или сочетанием клавиш <Ctrl>
+<4>
. Этот оператор чаще оказывается полезным не в матричной алгебре, а при организации циклов с индексированными переменными.
В том же листинге 7.4 (снизу) показано применение операции суммирования диагональных элементов квадратной матрицы. Эту сумму называют следом (trace) матрицы. Данная операция организована в виде встроенной функции tr:
tr (А) — след квадратной матрицы А.
Суммирование элементов
Листинг 7.4. Суммирование элементов и вычисление следа матрицы
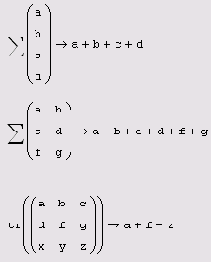
Перемножение матриц
Листинг 7.5. Перемножение матриц
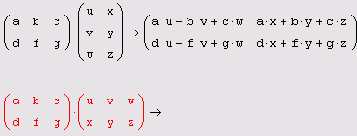
Обратите внимание (нижняя строка листинга 7.5), что попытка перемножить матрицы А и В несоответствующего (одинакового 2х3) размера оказалась безрезультатной: после введенного знака равенства находится пустой местозаполнитель, а само выражение в редакторе Mathcad выделяется красным цветом. При установке курсора на это выражение появляется сообщение о несовпадении числа строк первой матрицы с числом столбцов второй матрицы.
Еще один пример, относящийся к умножению вектора на матрицу-строку и, наоборот, строки на вектор, приведен в листинге 7.6.
ВНИМАНИЕ!
Тот же самый оператор умножения действует на два вектора по-другому (см. разд. 7.2.2).
Умножение вектора и строки
Листинг 7.6. Умножение вектора и строки
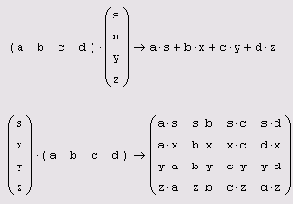
Аналогично сложению матриц со скаляром определяется умножение и деление матрицы на скалярную величину (листинг 7.7). Символ умножения вводится так же, как и в случае умножения двух матриц. На скаляр можно умножать матрицу любой размерности.
Умножение матрицы на скалярную величину
Листинг 7.7. Умножение матрицы на скалярную величину
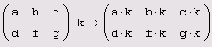
Модуль вектора
Листинг 7.8. Модуль вектора
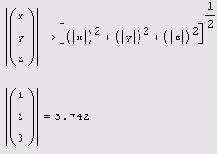
Скалярное произведение векторов
Листинг 7.9. Скалярное произведение векторов
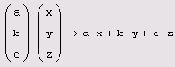
С осторожностью перемножайте несколько (более двух) векторов. По-разному расставленные скобки полностью изменяют результат умножения. Примеры такого умножения приведены в листинге 7.10.
Скалярное произведение
Листинг 7.10. Скалярное произведение векторов, умноженное на третий вектор

Векторное произведение двух векторов
Листинг 7.11. Векторное произведение двух векторов
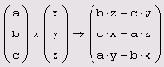
Использование оператора
Листинг 7.12. Использование оператора векторизации для перемножения элементов вектора
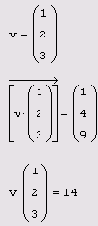
Большинство неспецифических функций Mathcad не требуют векторизации для проведения одной и той же операции над всеми элементами вектора. Например, аргументом тригонометрических функций по определению является скаляр. Если попытаться вычислить экспоненту от векторной величины, Mathcad осуществит векторизацию по умолчанию, возведя в степень е каждый элемент и выдав в качестве результата соответствующий вектор (листинг 7.13).
Векторизация аргумента
Листинг 7.13. Векторизация аргумента необязательна для большинства встроенных функций Mathcad

Вычисление определителя квадратной матрицы
Листинг 7.14. Вычисление определителя квадратной матрицы
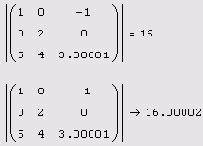
Вычисление ранга матрицы
Листинг 7.15. Вычисление ранга матрицы
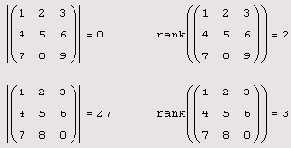
Вычисление обратной матрицы
Листинг 7.16. Вычисление обратной матрицы

Возведение квадратной матрицы в целую степень
Листинг 7.17. Возведение квадратной матрицы в целую степень
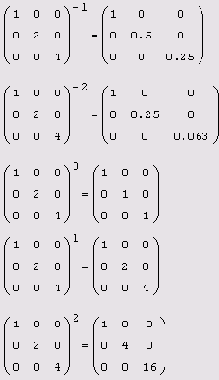
Вычисление различных норм матриц
Листинг 7.18. Вычисление различных норм матриц

Вычисление чисел
Листинг 7.19. Вычисление чисел обусловленности матриц (в различных нормах)
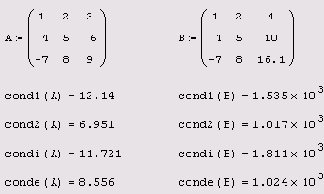
Создание матрицы на основе функции пользователя
Листинг 7.20. Создание матрицы на основе функции пользователя
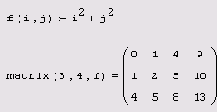
Создание матриц для построения 3D графиков
Для создания матриц имеются еще две специфические функции, применяемые, в основном, для быстрого и эффектного представления каких-либо зависимостей в виде трехмерных графиков (типа поверхности или пространственной кривой). Все их аргументы, кроме первого (имени функции), необязательны. Рассмотрим первую из этих встроенных функций.
CreateSpace(F( или fI, f2, f3) , t0,t1,tgrid,fmap) — создание вложенного массива, представляющего х-, у- и z-координаты параметрической пространственной кривой, заданной функцией F:
F(t) — векторная функция из трех элементов, заданная параметрически относительно единственного аргумента t;
f1(t) ,f2 (t), f3 (t) — скалярные функции;
t0 — нижний предел t (по умолчанию -5);
t1 — верхний предел t (по умолчанию 5);
tgrid — число точек сетки по переменной t (по умолчанию 20);
fmap — векторная функция от трех аргументов, задающая преобразование координат.
Пример использования функции CreateSpace показан на Рисунок 7.2. Заметьте, для построения графика кривой не потребовалось никакого дополнительного кода, кроме определения параметрической зависимости в вектор-функции F!
Создание единичной
Листинг 7.21. Создание единичной и диагональной матрицы заданной размерности
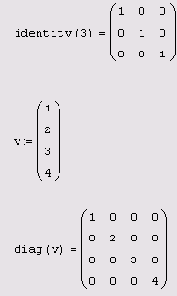
Доступ к отдельным
Листинг 7.22. Доступ к отдельным элементам, столбцам и строкам матрицы
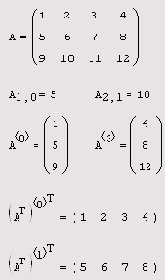
Примечание 1
Примечание 1
Выделить из матрицы один столбец или строку можно и с помощью функции submatrix (листинг 7.23, нижняя строка).
Примечание 2
Примечание 2
Те же операции применимы к матрицам-векторам и матрицам-строкам. Следует помнить только, что размер их составляет Nx1 и 1xN соответственно.
Выделение подматрицы
Листинг 7.23. Выделение подматрицы

Слияние матриц
Для того чтобы составить из двух или более матриц одну, в Mathcad предусмотрена пара матричных функций (листинг 7.24):
augment (А, B, C, . ..) — матрица, сформированная слиянием матриц-аргументов слева направо; stack (А, B, C, . ..) — матрица, сформированная слиянием матриц-аргументов сверху вниз:
А, B, C, . .. — векторы или матрицы соответствующего размера.
Примеры слияния матриц
Листинг 7.24. Примеры слияния матриц
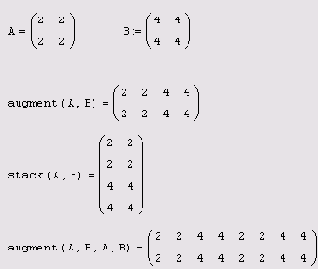
Специфические преобразования матриц
Еще две встроенных функции Mathcad позволяют создавать матрицы на основе некоторой имеющейся матрицы (листинг 7.25):
geninv (A) — создание матрицы, обратной (слева) прямоугольной матрице А; rref (А) — преобразование матрицы или вектора А в ступенчатый вид:
А — матрица, составленная из действительных чисел.
Примечание 3
Примечание 3
Размер NxM матрицы А для функции geninv должен быть таким, чтобы M>
M.
Создание матриц на основе другой матрицы
Листинг 7.25. Создание матриц на основе другой матрицы
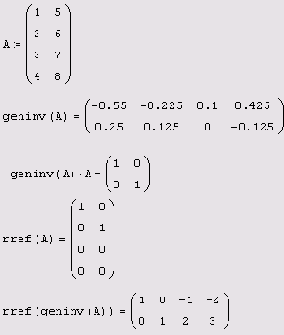
Сортировка вектора
Листинг 7.26. Сортировка вектора
Сортировка матриц по строке и столбцу
Листинг 7.27. Сортировка матриц по строке и столбцу
Размер матриц
Листинг 7.28. Размер матриц
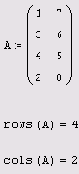
Размер векторов
Листинг 7.29. Размер векторов
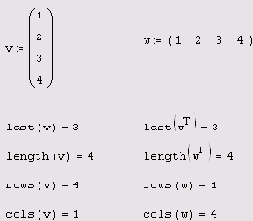
Простейшие матричные операции
7.1. Простейшие матричные операции
Простейшие операции матричной алгебры реализованы в Mathcad в виде операторов, причем их запись максимально приближена к математическому значению. Каждый оператор выражается соответствующим символом. Некоторые операции применимы только к квадратным матрицам NxN, некоторые допускаются только для векторов (например, скалярное произведение), а другие, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.
Векторная алгебра
7.2. Векторная алгебра
Векторы являются частным случаем матриц размерности NXI, поэтому для них справедливы все те операции, что и для матриц, если ограничения особо не оговорены. Вместе с тем для векторов в линейной алгебре предусмотрен целый ряд специфических операций, и все они реализованы в системе Mathcad.
ВНИМАНИЕ!
Непосредственное проведение многих векторных операций над матрицами-строками, т. е. матрицами 1xN, невозможно; для того, чтобы превратить строку в вектор, ее нужно предварительно транспонировать.
Вспомогательные матричные функции
7.4. Вспомогательные матричные функции
Перечислим основные встроенные функции, предназначенные для облегчения работы с векторами и матрицами. Они нужны для создания матриц, слияния и выделения части матриц, получения основных свойств матриц и т. п.
Ввод матриц и основные операции
Рисунок 7.1. Ввод матриц и основные операции над ними осуществляются при помощи панели Matrix
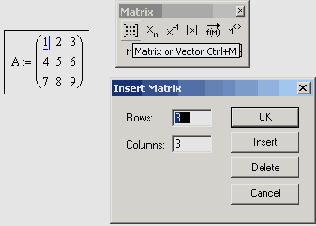
Примечание 1
Примечание 1
Все матричные и векторные операторы, о которых пойдет речь, допустимо использовать как в численных, так и в символьных расчетах. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными. Смело используйте символьный процессор в качестве мощного математического справочника, когда вы хотите вспомнить какое-либо определение из области линейной алгебры. Именно по этой причине мы прибегаем к примерам символьных расчетов в большинстве иллюстраций к данному разделу.
Вычисление определителей и обращение квадратных матриц
7.3. Вычисление определителей и обращение квадратных матриц
Рассмотрим еще несколько исключительно важных действий линейной алгебры, связанных с понятием определителя матрицы. Несмотря на то, что некоторые из них реализованы в Mathcad также в виде операторов, они требуют (при проведении расчетов по численным алгоритмам) несравненно больше внимания, нежели операторы упомянутые в двух предыдущих разделах.