Переопределенные системы
8.2.1. Переопределенные системы
Начнем разговор о "плохих" СЛАУ с переопределенными условиями, в которых число уравнений больше числа неизвестных.
О постановке задач
Чаще всего СЛАУ с прямоугольной матрицей размера MxN (при M>N, т. е. при числе уравнений большем числа неизвестных) вовсе не имеет решения, т. е. является несовместной, или переопределенной.
СЛАУ с треугольной матрицей
8.3.1. СЛАУ с треугольной матрицей
Начнем разговор о решении СЛАУ посредством матричных разложений с простого, но исключительно важного частного случая, а именно, систем с треугольной матрицей, т. е. такой матрицей, по одну из сторон от диагонали которой находятся одни нули. В листинге 8.17 приведен пример верхнетреугольной L матрицы (первая строка листинга), а также ряд формул, по которым за N операций рассчитывается решение соответствующей линейной системы. Из этого примера ясно, что сведение задачи общего вида к СЛАУ с треугольной матрицей практически решает эту задачу, поскольку гарантировано получение результата за минимальное число операций.
Примечание 1
Примечание 1
Подчеркнем, что мы нарочно оформили расчет решения треугольной СЛАУ в виде пользовательской функции trg (A,b), для чего нам пришлось применить элементы программирования. Мы так поступили, чтобы иметь впоследствии возможность применять ее в качестве подпрограммы решения СЛАУ посредством различных матричных разложений, включая листинг 8.17 в последующие листинги. Более того, несложно модифицировать листинг 8.17 для решения нижнетреугольных систем, определив, таким образом, еще одну функцию itrg (А, b) (вы найдете соответствующий листинг на компакт-диске).
Примечание 2
Примечание 2
Алгоритм решения СЛАУ с треугольной матрицей называют иногда прямым ходом решения СЛАУ (часто подразумевая, что до него выполнены определенные преобразования, именуемые обратным ходом) либо просто подстановкой. В частности, решение еще одного часто встречающегося типа систем с трехдиагональной матрицей сводится к прямому и обратному ходу алгоритма, называемого прогонкой (см. разд. 11.2.2).
Вычислительный блок Given/ Find
8.1.1. Вычислительный блок Given/ Find
Для того чтобы численным методом решить СЛАУ при помощи вычислительного блока (он был подробно описан в главе 5), следует после ключевого слова Given выписать ее, пользуясь логическими операторами. Рассмотрим в качестве примера систему трех уравнений, приведенную в листинге 8.1 (после ключевого слова Given). Неизвестными являются три компонента вектора х, поэтому именно эта векторная переменная является аргументом встроенной функции Find(x), решающей систему в последней строке листинга. Очень важно, что при использовании вычислительного блока Given/Find всем неизвестным требуется присвоить начальные значения, как это сделано в первой строке листинга 8.1.
Примечание 1
Примечание 1
Если матрица СЛАУ является невырожденной (точнее, если ее число обусловленности не слишком велико), то известно, что численное решение системы уравнений единственно. Поэтому начальные значения могут быть произвольными, т. к. результат работы численного метода все равно сойдется к точному решению.
Функция lsolve
8.1.2. Функция lsolve
Альтернативой способу решения СЛАУ, введенному в предыдущем разделе, является применение встроенной функции isolve. Для этого система уравнений должна быть записана в матричной форме Аx=b:
isolve (А, b) — вектор решения системы линейных алгебраических уравнений:
А — матрица коэффициентов системы; b — вектор правых частей.
Примечание 1
Примечание 1
В функции isolve запрограммирован численный метод LU-разложения (см. разд. 8.3.3), основанный на алгоритме последовательных исключений Гаусса. Он состоит в преобразовании матрицы А линейной системы к треугольному виду, т. е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми (с/и. разд. 8.3.1). Точнее, исходная СЛАУ Ах=b заменяется эквивалентной системой с другой матрицей А* и другим вектором правых частей b*, но имеющей то же решение, что и исходная система. Очень важно заметить, что результат, выдаваемый методом Гаусса, является точным (конечно, с поправкой на неизбежно присутствующие ошибки численного округления, которые, в случае хорошо обусловленной матрицы А, являются ничтожными). Таким образом, в противоположность применению вычислительного блока Given/Find (в основе которого лежит приближенный итерационный алгоритм), функция isolve не нуждается в присвоении начальных значений вектору x.
Применение функции isolve показано в листинге 8.4. При этом матрица А может быть определена любым из способов, необязательно явно, как во всех примерах этого раздела. В последней строке листинга осуществляется вычисление нормы невязки, которая оказывается равной нулю. Заметим, что встроенную функцию isolve допускается применять и при символьном решении СЛАУ (листинг 8.5). В последнем случае в уравнениях допускается использовать параметры (т. е. имена переменных, которым не присвоены никакие значения).
Недоопределенные системы
8.2.2. Недоопределенные системы
Альтернативным рассмотренному в предыдущем разделе классу СЛАУ с прямоугольной матрицей размера MxN, (при M<N) является случай, когда количество уравнений меньше количества неизвестных. Как несложно сообразить, такие системы либо имеют бесконечное число решений, либо не имеют решения вовсе. Решение несовместной системы можно искать в смысле минимизации нормы невязки по методу наименьших квадратов (см. разд. 8.2.1 и 8.2.3). Ниже в этом разделе будут разобраны задачи, имеющие бесконечное множество решений.
О постановке задач
Пример аналитического решения системы двух уравнений с тремя неизвестными при помощи символьного процессора приведен в листинге 8.11.
Разложение Холецкого
8.3.2. Разложение Холецкого
Разложением Холецкого симметричной (т. е. содержащей одинаковые элементы на местах, расположенных симметрично относительно главной диагонали) матрицы А является представление вида A=LLT, где L — треугольная матрица. Алгоритм Холецкого реализован во встроенной функции choiesky:
choiesky (А) — разложение Холецкого:
А — квадратная, положительно определенная симметричная матрица.
Пример разложения Холецкого приведен в листинге 8.18. Обратите внимание, что в результате получается верхняя треугольная матрица (нули сверху от диагонали), а транспонированная матрица является нижней треугольной. В последней строке листинга приведена проверка правильности найденного разложения.
Примечание 1
Примечание 1
Исходя из математического вида разложения Холецкого, матрицу L иногда называют квадратным корнем матрицы А.
LUразложение
8.3.3.LU-разложение
LU-разложением матрицы А, или треугольным разложением, называется матричное разложение вида PA=LU, где L и U — нижняя и верхняя треугольные матрицы соответственно, ар— (диагональная) матрица перестановок, P, А, L, и — квадратные матрицы одного порядка:
lu (A) — LU-разложение матрицы:
А — квадратная матрица.
Результатом работы встроенной функции LU-разложения является матрица, составленная из матриц L и и соответственно. Чтобы выделить сами матрицы LU-разложения, а именно, P, L, U, необходимо применить функцию выделения подматрицы submatrix (листинг 8.20).
Вырожденные и плохо обусловленные системы
8.2.3. Вырожденные и плохо обусловленные системы
Вернемся вновь к СЛАУ Aх=b с квадратной матрицей А размера MхN, которая, в отличие от рассмотренного выше "хорошего" случая (см. разд. 8. Г), требует специального подхода. Обратим внимание на два похожих типа СЛАУ:
вырожденная система (с нулевым определителем |А|=0); плохо обусловленная система (определитель А не равен нулю, но число обусловленности очень велико).
Несмотря на то, что эти типы систем уравнений существенно отличаются друг от друга (для первого решение отсутствует, а для второго существует и единственно), с практической точки зрения вычислителя, между ними много общего.
Вырожденные СЛАУ
Вырожденная система — это система, описываемая матрицей с нулевым определителем |A|=0 (сингулярной матрицей). Поскольку некоторые уравнения, входящие в такую систему, представляются линейной комбинацией других уравнений, то фактически сама система является недоопределенной. Несложно сообразить, что, в зависимости от конкретного вида вектора правой части ь, существует либо бесконечное множество решений, либо не существует ни одного. Первый из вариантов сводится к построению нормального псевдорешения (т. е. выбора из бесконечного множества решений такого, которое наиболее близко к определенному, например, нулевому, вектору). Данный случай был подробно рассмотрен в разд. 8.2.2 (см. листинги 8.11—8.13).
QRразложение
8.3.4. QR-разложение
Среди матричных разложений особую роль играют ортогональные преобразования, обладающие свойством сохранения нормы вектора. Напомним из курса линейной алгебры, что матрица Q называется ортогональной, если QTQ=I, где I — единичная матрица. Свойство сохранения нормы вектора при ортогональных преобразованиях, т. е. |Qx|=|x|, дает рецепт поиска псевдорешения вырожденных СЛАУ, а именно, замену исходной задачи минимизации невязки с "плохой" матрицей |Аx-b| задачей |QT(Ax-b)|, в которой матрица уже будет "хорошей" благодаря специальному построению матрицы Q. Таким образом, ортогональные разложения используются при решении любых систем (в том числе с прямоугольной матрицей А, причем как переопределенных, так и недоопределенных).
Одним из важнейших вариантов ортогональных разложений некоторой матрицы А является QR-разложение вида A=QR, где Q — ортогональная матрица, а R — верхняя треугольная матрица:
qr (A) — QR-разложение:
А — вектор или матрица любого размера.
Результатом действия функции qr (А) является матрица, составленная из матриц Q и R соответственно (подобно рассмотренному в предыдущем разделе LU-разложению). Выделить матрицы QR-разложения несложно при помощи встроенной функции выделения подматрицы submatrix (листинг 8.22).
SVD(сингулярное) разложение
8.3.5. SVD-(сингулярное) разложение
Наиболее эффективными (но и ресурсоемкими) средствами решения произвольных СЛАУ (с матрицей А размера NxM) по методу наименьших квадратов являются так называемые полные ортогональные разложения, имеющие, по определению, вид A=UKVT.
Здесь U и V — ортогональные матрицы размером NxN и MхM соответственно, а k— матрица размера NxM, имеющая следующую структуру:
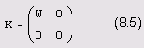
причем w — матрица размера kxk, где k — ранг исходной матрицы А.
Самое известное из ортогональных, SVD- (singular value decomposition) или сингулярное разложение — разложение вида A=USVT, где S — диагональная матрица, состоящая из нулей и расположенных на диагонали сингулярных чисел матрицы А. Расчет сингулярного разложения в Mathcad осуществляется при помощи пары встроенных функций:
svds (A) — вектор, состоящий из сингулярных чисел; svd (A) — сингулярное разложение:
А — действительная матрица.
Пример поиска сингулярного разложения сингулярной матрицы приведен в листинге 8.25, причем его последняя строка представляет собой проверку правильности найденного разложения. Подчеркнем, что вычисленные сингулярные числа находятся на главной диагонали средней матрицы разложения, а ее остальные элементы, по определению, равны нулю. Сравнивая матрицы из листинга 8.25, вы без труда разберетесь, каким образом следует выделять искомые матрицы сингулярного разложения из результата, поставляемого функцией svd.
Графическое представление несовместной
Рисунок 8.7. Графическое представление несовместной системы двух уравнений с сингулярной матрицей
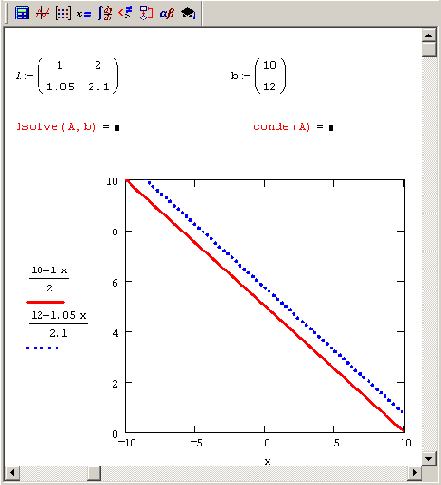
Рассмотрим второй случай, когда СЛАУ Aх=b с сингулярной квадратной матрицей А не имеет ни одного решения. Пример такой задачи (для системы двух уравнений) проиллюстрирован Рисунок 8.7, в верхней части которого вводятся матрица А и вектор b, а также предпринимается (неудачная, поскольку матрица А сингулярная) попытка решить систему при помощи функции isolve. График, занимающий основную часть рисунка, показывает, что два уравнения, задающие систему, определяют на плоскости (x0,xi) две параллельные прямые. Прямые не пересекаются ни в одной точке координатной плоскости, и решения системы, соответственно, не существует.
Примечание 1
Примечание 1
Во-первых, заметим, что СЛАУ, заданная несингулярной квадратной матрицей размера 2x2, определяет на плоскости пару пересекающихся прямых (см. Рисунок 8.9 ниже). Во-вторых, стоит сказать, что, если бы система была совместной, то геометрическим изображением уравнений были бы две совпадающие прямые, описывающие бесконечное число решений.
График функции f (х2) = |х| при
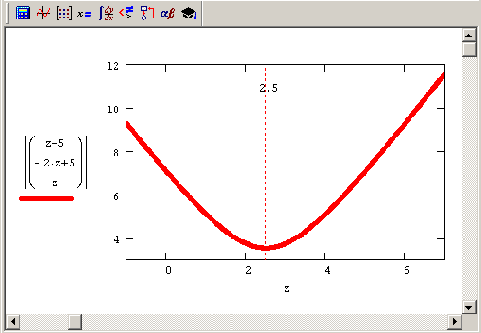
Рисунок 8.6. График функции f (х2) = |х| при условии выполнения СЛАУ из листинга 8.13
Принимая во внимание введенную технику
Рисунок 8.5. График функции f (x0) = |х| при условии, что xc-2xi=10
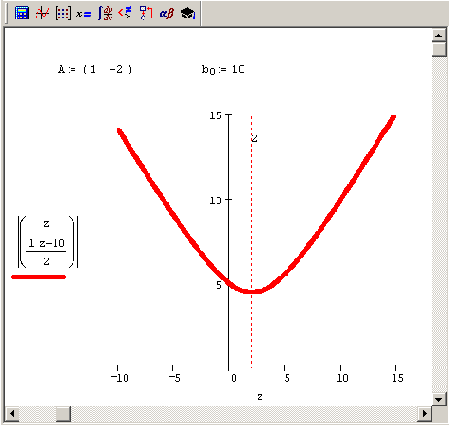
Принимая во внимание введенную технику решения недоопределенных СЛАУ, можно предложить для этих задач простой и понятный алгоритм, опирающийся на встроенную функцию Minimize. В листинге 8.12 решена задача численного отыскания псевдорешения рассматриваемого единственного уравнения (Рисунок 8.5), а в листинге 8.13 — решение недоопределенной системы двух уравнений с тремя неизвестными, которая исследовалась аналитически в листинге 8.11 (см. предыдущий разд.). Как уже отмечалось, смысл обоих листингов заключается в минимизации нормы искомого вектора при условии, что выполнена система равенств Aх=b. Графики функции f (х) = |х|, при условии выполнения СЛАУ из листингов 8.12 и 8.13, изображены на Рисунок 8.5 и 8.6 соответственно.
График хорошо обусловленной системы двух уравнений
Рисунок 8.9. График хорошо обусловленной системы двух уравнений
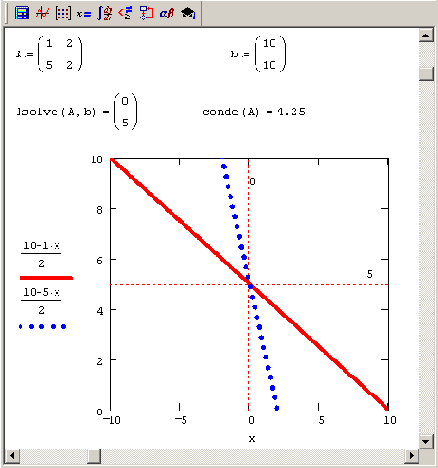
График минимизируемой функции невязки f (х) = | Ахb|
Рисунок 8.1. График минимизируемой функции невязки f (х) = | Ах-b|
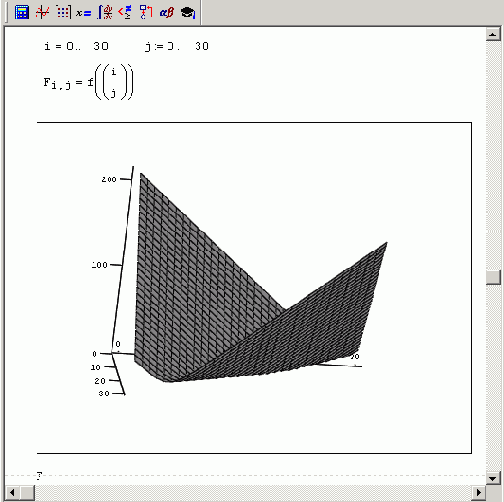
График плохо обусловленной системы двух уравнений
Рисунок 8.10. График плохо обусловленной системы двух уравнений
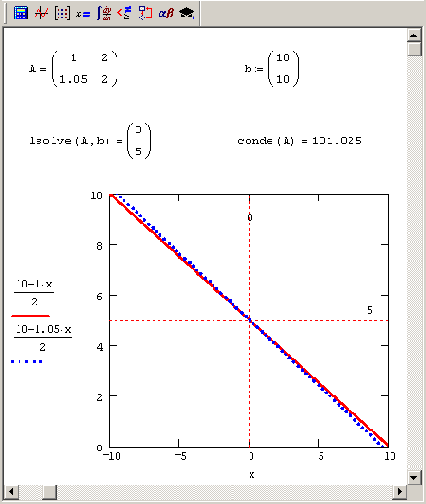
Из Рисунок 8.10 видно, что прямые, соответствующие плохо обусловленной СЛАУ, располагаются в непосредственной близости друг от друга (почти параллельны). В связи с этим малые ошибки в расположении каждой из прямых могут привести к значительным погрешностям локализации точки их пересечения (решения СЛАУ) в противоположность случаю хорошо обусловленной системы, когда малые погрешности в наклоне прямых мало повлияют на место точки их пересечения (Рисунок 8.9).
Примечание 2
Примечание 2
Плохая обусловленность матрицы типична и при реконструкции экспериментальных данных, задаваемых переопределенными (несовместными) СЛАУ (например, в задачах томографии). Именно такой случай приведен в качестве примера в следующем разделе (см. листинг 8.16 ниже).
Метод регуляризации
Для решения некорректных задач, в частности, вырожденных и плохо обусловленных СЛАУ, разработан очень эффективный прием, называемый регуляризацией. В его основе лежит учет дополнительной априорной информации о структуре решения (векторе априорной оценки хо), которая очень часто присутствует в практических случаях. В связи с тем, что регуляризация была подробно рассмотрена в разд. 6.3.3, напомним лишь, что задачу решения СЛАУ Аx=b можно заменить задачей отыскания минимума функционала Тихонова:
?(х,?) = |Ах-b|2+?|х-х0|2. (8.3)
Здесь Я, — малый положительный параметр регуляризации, который необходимо подобрать некоторым оптимальным способом. Можно показать, что задачу минимизации функционала Тихонова можно, в свою очередь, свести к решению другой СЛАУ:
(АTА+?I)-х=АTВ+?х0, (8.4)
которая при ?->0 переходит в исходную плохо обусловленную систему, а при больших x, будучи хорошо обусловленной, имеет решение х0. Очевидно, оптимальным будет некоторое промежуточное значение А, устанавливающее определенный компромисс между приемлемой обусловленностью и близостью к исходной задаче. Отметим, что регуляризационный подход сводит некорректную задачу к условно-корректной (по Тихонову) задаче отыскания решения системы (8.4), которое, в силу линейности задачи, является единственным и устойчивым.
Приведем, без излишних комментариев, регуляризованное решение вырожденной системы, которая была представлена на Рисунок 8.8.
График сечений функции невязки f (х) = |Ахb|
Рисунок 8.8. График сечений функции невязки f (х) = |Ах-b|
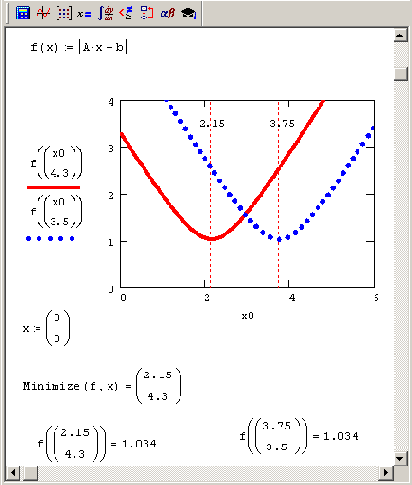
Несложно догадаться, что в рассматриваемом сингулярном случае псевдорешений системы, минимизирующих невязку |Ax-b|, будет бесконечно много, и лежать они будут на третьей прямой, параллельной двум показанным на Рисунок 8.7 и расположенной в середине между ними. Это иллюстрирует Рисунок 8.8, на котором представлено несколько сечений функции f(x)= = | Аx-b |, которые говорят о наличии семейства минимумов одинаковой глубины. Если попытаться использовать для их отыскания встроенную функцию Minimize, ее численный метод будет всегда отыскивать какую-либо одну точку упомянутой прямой (в зависимости от начальных условий). Поэтому для определения единственного решения следует выбрать из всего множества псевдорешений то, которое обладает наименьшей нормой. Можно пытаться оформить данную многомерную задачу минимизации в Mathcad при помощи комбинаций встроенных функций Minimize, однако более эффективным способом будет использование регуляризации (см. ниже) или ортогональных матричных разложений (см. разд. 8.3).
Плохо обусловленные системы
Плохо обусловленная система — это система, у которой определитель А не равен нулю, но число обусловленности |А-1| |А| очень велико. Несмотря на то, что плохо обусловленные системы имеют единственное решение, на практике искать это решение чаще всего не имеет смысла. Рассмотрим свойства плохо обусловленных СЛАУ на двух конкретных примерах (листинг 8.14).
Способ выбора одного решения из
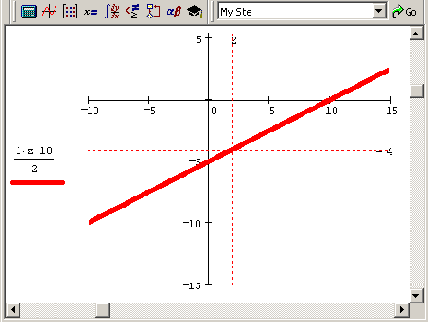
Рисунок 8.4. График всех решений уравнения x0-2x1=10
Нормальное псевдорешение
Способ выбора одного решения из бесконечного множества, изображенного на Рисунок 8.4, подсказывает, по аналогии с переопределенными СЛАУ (см. разд. 8.2. Т), сам физический смысл задачи, которую можно интерпретировать как м измерений с N неизвестными (M<N). Для того чтобы получить разумное единственное решение задачи, необходимо "доопределить" ее, добавив некоторые априорные соображения о значении неизвестного вектора х.
Если априорной информации о примерной величине вектора х нет, единственным образом решить СЛАУ невозможно. Однако если о неизвестном векторе хоть что-то можно сказать, данная информация позволит доопределить систему уравнений и получить решение, учитывающее как систему, так и априорную информацию. Иными словами, следует ввести в задачу определенные ожидания о величине вектора х. Математически, не теряя общности, можно полагать ожидаемое значение вектора х нулевым, поскольку перейти от любого х к нуль-вектору можно простым линейным преобразованием переменных, которое изменит только вектор правой части b.
Таким образом, вполне логично объявить решением недоопределенной СЛАУ такое из решений, которое ближе всего находится к нулевому вектору, т. е. обладает минимальной нормой |х| -min. Это решение называют нормальным псевдорешением СЛАУ, и искать его следует, минимизируя норму вектора х на предварительно полученном семействе решений СЛАУ. Иными словами, решение недоопределенной СЛАУ сводится к условной минимизации функции |х| (Рисунок 8.5). Геометрический смысл нормального псевдорешения (в рассматриваемом случае одного уравнения с двумя неизвестными) очевиден: это точка, лежащая на пересечении прямой семейства всех решений и перпендикуляра к этой прямой, восстановленного из начала координат. На Рисунок 8.4 нормальное псевдорешение выделено пунктирными линиями.
Хорошо обусловленные системы с квадратной матрицей
8.1. Хорошо обусловленные системы с квадратной матрицей
С вычислительной точки зрения, решение СЛАУ с квадратной матрицей А не представляет трудностей, если размерность А не очень велика. С большой матрицей проблем также не возникает, если она не очень плохо обусловлена (конечно, надо учитывать, что объем вычислений возрастает с увеличением размерности матрицы). В данном разделе будут рассмотрены именно такие системы, решение которых реализовано в Mathcad в двух вариантах:
вычислительный блок Given/Find (приближенный итерационный алгоритм); встроенная функция isoive (точный алгоритм Гаусса).
При этом СЛАУ можно решать как в более наглядной форме (8.1), так и в более компактной матричной форме (8.2). Для первого способа следует использовать блок Given/Find (он может также применяться в случае систем уравнений и неравенств, а также при решении переопределенных СЛАУ), а для второго — как вычислительный блок, так и встроенную функцию isoive.
Изменение численного алгоритма для функции Minerr
Рисунок 8.3. Изменение численного алгоритма для функции Minerr
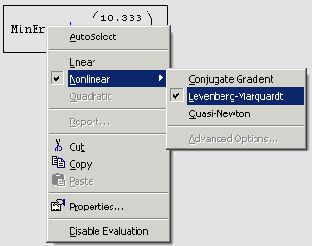
Во-вторых, приближенное решение СЛАУ посредством вычислительного блока Given/Minerr невозможно при наличии дополнительных условий, выражающих вспомогательную априорную информацию о постановке задачи. В частности, математически более правильным было решать нашу задачу о яблоках и грушах с дополнительным условием положительной определенности компонент неизвестного вектора (поскольку масса фруктов по определению больше нуля). В результате исходная задача сводится к условной минимизации функции f (х), что в Mathcad-программе соответствует появлению дополнительных неравенств после ключевого слова Given (см. пример ниже, решенный в листинге 8. 10). Однако все уравнения и неравенства, предшествующие функции Minerr, будут восприниматься численным процессором Mathcad одинаково, т. е. не в качестве жестких условий, а как выражения, которые должны выполняться лишь с некоторой точностью. В результате найденное решение может вовсе не отвечать условию положительной определенности (этот вопрос обсуждался в разд. 6.2, когда речь шла о задачах оптимизации).
В свете перечисленных проблем применение функции Minimize для поиска псевдорешения СЛАУ выглядит более обоснованным. К слову заметим, что выбор любого из трех нелинейных численных алгоритмов минимизации приводит к одинаковым результатам (листинг 8.9). Функция Minimize годится и для отыскания псевдорешения с дополнительными условиями, выражающими имеющуюся априорную информацию. Соответствующий пример иллюстрирует листинг 8.10, в котором осуществляется поиск псевдорешения СЛАУ, немного отличающейся от рассмотренной выше. Это отличие приводит к тому, что при использовании той же самой методики получается отрицательное решение (третья строка листинга). При добавлении в задачу дополнительных условий результат минимизации оказывается другим (последняя строка листинга 8.10).
Примечание 3
Примечание 3
Несколько иной подход к переопределенным системам, для которых имеется дополнительная информация другого типа (а именно, априорная оценка неизвестного вектора х), будет изложен в следующем разделе.
демонстрирует запись
Листинг 8.1 демонстрирует запись каждого уравнения системы (в промежутке между Given и Find), что очень неудобно, когда система содержит большое число уравнений. В последнем случае намного лучше применить матричную запись СЛАУ, как это показано в листинге 8.2. Первая строка листинга представляет собой определение матрицы СЛАУ А и вектора правых частей ь, а в остальном работа блока Given/Find полностью идентична предыдущему листингу.
Решение СЛАУ с помощью вычислительного блока
Листинг 8.1. Решение СЛАУ с помощью вычислительного блока
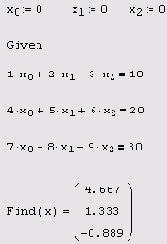
Решение СЛАУ записанной в матричной форме
Листинг 8.2. Решение СЛАУ, записанной в матричной форме
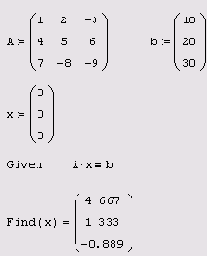
Проверка правильности решения СЛАУ прямой подстановкой, причем в матричной форме, приведена в листинге 8.3. Обратите внимание на матрицу в первой строке листинга, представляющую рассматриваемую систему уравнений. Во второй строке листинга 8.3 производится вычисление нормы невязки, характеризующей точность полученного решения СЛАУ.
Примечание 2
Примечание 2
Такая большая невязка может вызвать совершенно обоснованное удивление читателя. На самом деле точность решения гораздо выше (в данном примере ~10-15, а полученное значение невязки -10-3 объясняется соответствующим представлением вещественных чисел результата на экране (по умолчанию с точностью до 3-го знака).
Проверка правильности решения СЛАУ
Листинг 8.3. Проверка правильности решения СЛАУ
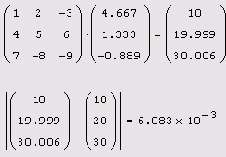
Численное решение СЛАУ
Листинг 8.4. Численное решение СЛАУ
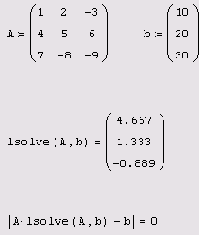
Символьное решение
Листинг 8.5. Символьное решение СЛАУ (продолжение листинга 8.4)
="6.gif">
демонстрирует что
Листинг 8.6 демонстрирует, что несовместные системы не могут быть решены ни при помощи встроенной функции isolve, ни посредством вычислительного блока Given/Find.
Попытка решения несовместных СЛАУ
Листинг 8.6. Попытка решения несовместных СЛАУ
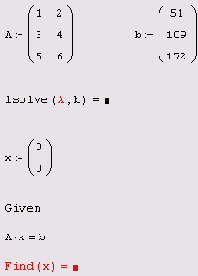
Примечание 1
Примечание 1
Конечно, в редких случаях система с прямоугольной матрицей может оказаться совместной (если выбран соответствующий вектор ь), как это показано в листинге 8.7. Любопытно, что итерационный алгоритм блока Given/Find справляется с такой задачей, а алгоритм исключения, заложенный в функции Isolve, — нет.
может описывать случай
Листинг 8.7 может описывать случай, когда погрешность эксперимента полностью отсутствует, и система трех уравнений с двумя неизвестными оказывается совместной. А листинг 8.6 является примером куда более типичной ситуации, когда погрешность каждого измерения приводит к тому, что итоговая СЛАУ оказывается несовместной, т. е. не имеет никакого точного решения.
Примечание 2
Примечание 2
Простой пример с яблоками и грушами является типичным представителем класса обратных задач, подразумевающих, в частности, восстановление неизвестных входных данных эксперимента по наблюдаемым выходным характеристикам (получаемым в условиях наличия погрешности). Для таких задач развиты специальные методы решения, наиболее простой из которых мы приводим в этом и следующем разделах (не останавливаясь на его обосновании, которое потребовало бы привлечения дополнительных соображений из области математической статистики).
Псевдорешение (метод наименьших квадратов)
Напрашивающийся сам собой путь решения нашего простого примера с грушами и яблоками является хорошей иллюстрацией подхода к общей проблеме переопределенных СЛАУ. А именно, вместо точного решения системы уравнений следует организовать поиск такого вектора х, который будет наилучшим образом удовлетворять всем уравнениям, т. е. минимизировать их невязку (расхождение между вектором Aх и вектором правой части СЛАУ b). Поскольку невязка Аx-b является векторной величиной, то, исходя из практических соображений, минимизации надо подвергать ее норму (т. е. скаляр) |Аx-b|. Этот подход позволит, с одной стороны, получить разумное, с физической точки зрения, решение задачи, а, с другой — использовать полезную информацию, заключенную во всех уравнениях.
Таким образом, при интерпретации переопределенных СЛАУ принято искать не точное решение (которого, как уже отмечалось, при данной постановке задачи просто нет), а псевдорешение — вектор, минимизирующий норму невязки системы уравнений. Таким образом, задача решения линейной системы уравнений заменяется задачей отыскания глобального минимума функции f (x) = |Аx-b|. Повторимся еще раз, что, в полном соответствии с обозначениями, принятыми в Mathcad, х — это неизвестный вектор, а символ модуля (две вертикальные черты) означает операцию вычисления нормы (евклидовой длины вектора). Поскольку эта минимизируемая норма зависит от суммы квадратов компонент неизвестного вектора, то процедура поиска псевдорешения является ни чем иным, как реализацией метода наименьших квадратов (МНК).
График функции двух переменных f(x0,x1) показан в виде трехмерной поверхности на Рисунок 8.1, а несколько его сечений в окрестности минимума — на Рисунок 8.2. Нетрудно сообразить, почему структура функции оказывается именно такой, если вспомнить, что f(x)2
является квадратичной формой относительно неизвестных х0 и x1 Надо отметить, что если бы наша система имела большее число уравнений, то вычислительная задача соответствующим образом усложнилась бы, т. к. минимизацию следовало бы проводить не по двум, а по большему числу переменных.
Обращаясь к практической стороне дела, следует вспомнить, что для решения задач минимизации невязки системы уравнений (см. главу 6) в Mathcad предусмотрены две встроенные функции — Minerr и Minimize. Применение этих альтернативных средств иллюстрируется листингами 8.8 и 8.9 соответственно. В первом случае используется ключевое слово Given для ввода СЛАУ в матричной форме, а во втором — в явном виде определяется функция f(x), подлежащая минимизации. Обе встроенные функции, как вы помните, применяют итерационные численные алгоритмы, и поэтому требуют ввода начальных значений для всех неизвестных, т. е. нулевой итерации (вторая строка обоих листингов).
Пример нахождения
Листинг 8.7. Пример нахождения решения СЛАУ с прямоугольной матрицей
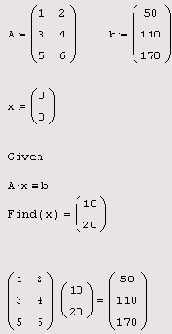
На практике (особенно в последнее время) задачи отыскания решения переопределенных СЛАУ встречаются довольно часто. Приведем простую интерпретацию переопределенной задачи, связанной с обработкой результатов какого-либо эксперимента, например, взвешивания предметов двух типов (для простоты и определенности, совершенно одинаковых яблок и одинаковых груш). Если, согласно постановке задачи, на весы можно положить любое количество предметов любого типа, то модель каждого акта взвешивания представится линейным уравнением, двумя неизвестными в которых будет масса яблока и масса груши. Очевидно, что чем больше взвешиваний мы проведем, тем точнее (в условиях присутствующей в эксперименте погрешности измерений) сможем определить искомые величины.
Обращаясь к числовым примерам листингов 8.6 и 8.7, легко сообразить, что они соответствуют трем актам взвешивания, когда в первый раз на весы кладется одно яблоко и две груши, во второй — три яблока и четыре груши, и в третий — пять яблок и шесть груш.
Поиск псевдорешения при помощи функции Minerr
Листинг 8.8. Поиск псевдорешения при помощи функции Minerr

Поиск псевдорешения при помощи функции Minimize
Листинг 8.9. Поиск псевдорешения при помощи функции Minimize
="13.gif">
На первый взгляд, удобнее использовать функцию Minerr, поскольку для нее текст Mathcad-программы (листинг 8.8) выглядит более приближенным к изначальной постановке задачи (а именно, найти приближенное решение заданной системы уравнений). Между тем, выбор функции Minerr таит в себе, по крайней мере, две опасности.
Во-первых, сравнивая результаты, можно с недоумением обнаружить, что они абсолютно различны, причем более похож на правильный ответ, выдаваемый функцией Minimize (об этом можно судить, опираясь на соображение ожидаемой близости псевдорешения к решению системы из листинга 8.7, от которого мы отошли лишь немного). Разгадка заключается в особенностях применения численного алгоритма, заложенного в функцию Minerr. По умолчанию решение линейной системы уравнений производится при помощи линейного алгоритма. Чтобы сменить его на нелинейный, необходимо нажатием правой кнопки мыши вызвать из области имени функции контекстное меню и сменить тип метода Linear (Линейный) на один из нелинейных методов Nonlinear (Нелинейный) (Рисунок 8.3). Однако даже в этом случае, как показывает опыт, наиболее правильный ответ получается только для одного из трех доступных численных алгоритмов.
Поиск псевдорешения
Листинг 8.10. Поиск псевдорешения при наличии априорной информации
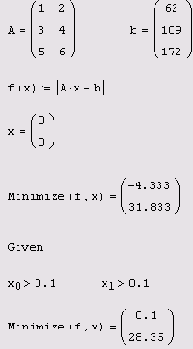
Аналитический поиск
Листинг 8.11. Аналитический поиск семейства решений недоопределенной СЛАУ
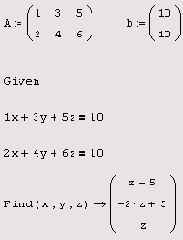
Приведенную простую систему двух уравнений нам удалось без труда решить аналитически, однако для решения недоопределенных систем, состоящих из большого числа уравнений, необходимо уметь использовать численные алгоритмы.
Рассмотрим в качестве еще одного модельного примера единственное уравнение с двумя неизвестными x0-2x1=l0. Хорошей визуализацией, подчеркивающей специфику данной задачи, будет график геометрического места его решений на плоскости (x0,xi) (Рисунок 8.4). Заметим, что на этом и на следующем рисунке мы использовали обозначение (для корректного построения графика) x0=z. Очевидно, что решений уравнения бесконечно много, и все они находятся на прямой линии x1=(x0-10) /2.
Как и в предыдущем примере (листинг 8.11), нам удалось решить задачу аналитически, и опять-таки число решений получилось бесконечным. Для того чтобы получить возможность осмысленного численного решения подобных (уже не настолько тривиальных) задач, необходимо выделить из бесконечного множества решений одно, оправданное с математической точки зрения, и предложить алгоритм его поиска. Эта проблема решается посредством привлечения понятия нормального псевдорешения.
Поиск нормального
Листинг 8.12. Поиск нормального псевдорешения уравнения x0-2xi=10
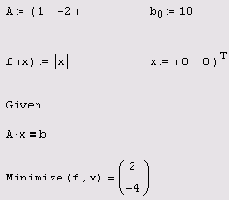
Примечание 1
Примечание 1
Возвращаясь к примеру с грушами и яблоками (см. разд. 8.2), можно интерпретировать недоопределенную СЛАУ из листинга 8.12 как единственное измерение, которого недостаточно для однозначного определения веса одной груши и одного яблока. Однако если учесть априорную оценку об этих весах (пусть даже весьма грубую), это позволит отыскать решение, которое будет осмысленным. Конечно, в этом случае следует выбрать соответствующий вектор априорной оценки (в третьей строке листинга 8.12) и, кроме того, добавить дополнительное условие на положительную определенность неизвестных, как в листинге 8.10 (см. раза. 8.2.2).
Поиск нормального
Листинг 8.13. Поиск нормального псевдорешения недоопределенной СЛАУ
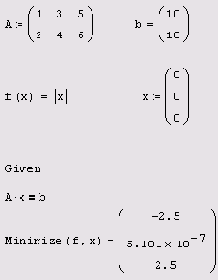
Примечание 2
Примечание 2
Если недоопределенная СЛАУ не имеет бесконечного множества решений, а является несовместной, то способ, предложенный в листинге 8.13, использовать нельзя, т. к. условие заведомо невыполнимо. Подход к решению таких задач заключается в поиске компромиссного решения, минимизирующего как норму невязки, так и норму решения (см. разд. 8.2.3).
Решение двух близких плохо обусловленных СЛАУ
Листинг 8.14. Решение двух близких плохо обусловленных СЛАУ
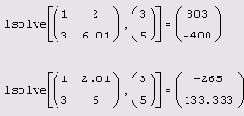
Каждая строка листинга 8.14 содержит решение двух очень близких плохо обусловленных СЛАУ (с одинаковой правой частью ь и мало отличающимися матрицами А). Несмотря на близость, точные решения этих систем оказываются очень далекими друг от друга. Надо заметить, что для системы двух уравнений точное решение получить легко, однако при решении СЛАУ большой размерности незначительные ошибки округления, неминуемо накапливаемые при расчетах (в том числе и "точным" алгоритмом Гаусса), приводят к огромным погрешностям результата. Возникает вопрос: имеет ли смысл искать численное решение, если заранее известно, что, в силу неустойчивости самой задачи, оно может оказаться совершенно неправильным?
Еще одно соображение, которое вынуждает искать специальные методы решения плохо обусловленных СЛАУ (даже приведенной в качестве примера в листинге 8.14 системы двух уравнений), связано с их физической интерпретацией как результатов эксперимента. Если изначально известно, что входные данные получены с некоторой погрешностью, то решать плохо обусловленные системы не имеет вовсе никакого смысла, поскольку малые ошибки модели (матрицы А и вектора ь) приводят к большим ошибкам решения. Задачи, обладающие такими свойствами, называются некорректными.
Чтобы лучше понять причину некорректности, полезно сравнить графическую интерпретацию хорошо (Рисунок 8.9) и плохо (Рисунок 8.10) обусловленной системы двух уравнений. Решение системы визуализируется точкой пересечения двух прямых линий, изображающих каждое из уравнений.
демонстрирует отыскание
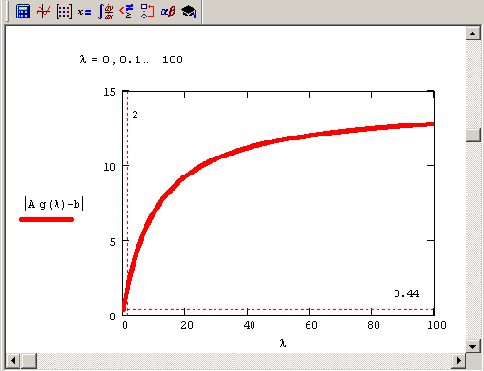
Листинг 8.15 демонстрирует отыскание решения задачи (8.4), а полученная зависимость невязки и самого решения от параметра регуляризации Я показана на Рисунок 8.11 и 8.12 соответственно. Важно подчеркнуть, что решения исходной системы и, следовательно, системы (8.4) при ?=0 не существует.
Регуляризация вырожденной СЛАУ
Листинг 8.15.Регуляризация вырожденной СЛАУ
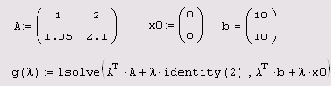
Заключительным шагом регуляризации является выбор оптимального ?. Имеется, по крайней мере, два соображения, исходя из которых, можно выбрать параметр регуляризации, если опираться на зависимость от него невязки. В рассматриваемом примере применим критерий определения ?, опирающийся -на подбор нормы невязки, равной априорной оценке погрешностей задания входных данных: матрицы А и вектора b, т. е. величине |?A| + |5?|. Например, можно выбрать норму невязки и, соответственно, параметр ? и решение х(?), которые отмечены на Рисунок 8.11 и 8.12 пунктирами.
Примечание 3
Примечание 3
Другим вариантом выбора ?, не требующим никаких априорных соображений относительно погрешностей модели, является так называемый квазиоптимальный метод, рассмотренный в разд. 6.3.3.
Примечание 4
Примечание 4
Полезно убедиться в том, что формула (8.4) в случае линейной задачи дает тот же результат, что и общая формула (8.3). Для этого достаточно изменить в листинге 8.15 последнюю строку, выражающую решение СЛАУ (8.4), на код, реализующий минимизацию численным методом, как это показано в листинге 8.16. Расчеты (которые требуют значительно большего компьютерного времени) дают тот же самый результат, что был приведен на Рисунок 8.11 и 8.12.
Примечание 5
Примечание 5
Попробуйте в расчетах листингов 8.15 и 8.16 взять иную, например, более реалистичную, априорную оценку решения (вместо использованного в них нулевого вектора х0) и посмотреть, как это повлияет на результат.
Регуляризация СЛАУ
Листинг 8.16. Регуляризация СЛАУ при помощи алгоритма минимизации (продолжение листинга 8.15)
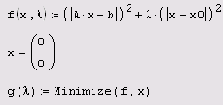
Решение СЛАУ с треугольной
Листинг 8.17. Решение СЛАУ с треугольной матрицей (прямой ход)
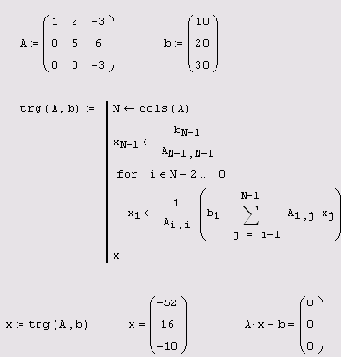
Разложение Холецкого
Листинг 8.18. Разложение Холецкого
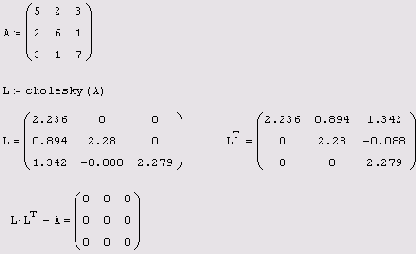
Решение СЛАУ, если разложение Холецкого для него известно, основано на замене исходной системы Аx=b другой системой b-у=b (где у=LTх), что иллюстрируется листингом 8.19. В первой строке листинга задается вектор правой части b и вычисляется стандартным методом Гаусса решение системы. В оставшейся части листинга СЛАУ решается при помощи разложения Холецкого, проведенного в листинге 8.18. После нахождения (простой подстановкой, т. к. матрица L — треугольная) вектора у, опять-таки подстановкой в уравнение у=LTх (т. к. LT — тоже треугольная матрица) отыскивается вектор х.
ВНИМАНИЕ!
В листинге 8.19 использованы пользовательские функции решения треугольных СЛАУ, описанные в предыдущем разделе. Если вы набираете листинг "от руки", их можно заменить универсальной встроенной функцией isolve.
Решение СЛАУ при
Листинг 8.19. Решение СЛАУ при помощи разложения Холецкого (продолжение листингов 8.18 и 8.17)

LUразложение
Листинг 8.20. LU-разложение
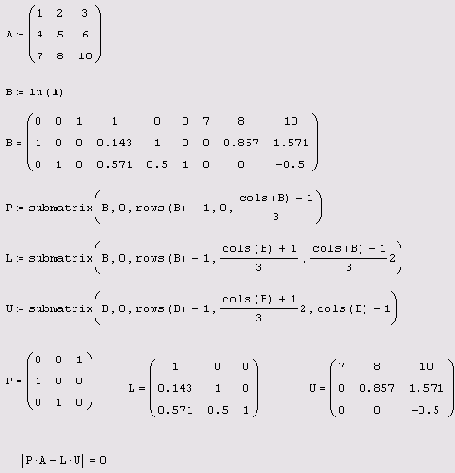
Треугольное разложение матрицы системы линейных уравнений производится при ее решении численным методом Гаусса. Фактически именно алгоритм LU-разложения заложен во встроенной функции isolve, применяемой для "точного" решения хорошо обусловленных систем (см. разд. 8.1.2). Таким образом, посредством LU-разложения можно решать СЛАУ с хорошо обусловленной матрицей д.
Почему метод LU-разложения является мощным средством решения СЛАУ и особенно важен при обработке соответствующих экспериментальных данных? Чтобы понять это, заменим исходную систему Аx=b эквивалентной системой PLUх=Pb, а ее, в свою очередь, парой других систем: Lу=Pb и Uх=у. Несложно сообразить, что обе системы решаются прямой подстановкой, т. к. матрицы PL и U — треугольные. Сначала из первой СЛАУ определяется промежуточный вектор у, а затем (из второй системы) — искомый вектор х. Главное преимущество метода LU-разложения заключается в том, что явный вид вектора правой части ь при решении СЛАУ используется только на заключительном этапе (в формулах прямого хода), а наиболее трудоемкие операции по вычислению самих матриц b и и вовсе не требуют знания вектора b. Таким образом, если решается серия СЛАУ с одной и той же матрицей А, но разными правыми частями b (что весьма характерно в обратных задачах интерпретации эксперимента), очень выгодно единожды вычислить LU-разложение матрицы А, а уже затем быстрой подстановкой решить каждую из конкретных систем. Сказанное иллюстрирует листинг 8.21, в котором решается две СЛАУ с матрицей из предыдущего листинга и различными векторами правых частей b.
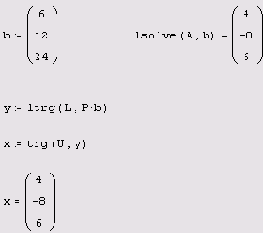
QRразложение сингулярной матрицы
Листинг 8.22. QR-разложение сингулярной матрицы

Если бы исходная СЛАУ Aх=b не была вырожденной, то можно было сразу записать: QTQ-Rx=QTb, откуда следует (благодаря ортогональности матрицы Q): Rx=QTb. Так как матрица к — треугольная, решение данной системы получается по формулам прямого хода. Если использовать нашу пользовательскую функцию решения треугольной системы (см. разд. 8.3. Т), то результат исходной СЛАУ запишется в виде одной строки кода: trg(R,QTb) (соответствующий пример решения невырожденной СЛАУ вы найдете на компакт-диске).
Обратимся теперь к проблеме решения СЛАУ с сингулярной квадратной NxN или прямоугольной NxM матрицей А. Если ее ранг равен k (он может быть меньше N и м, как в листинге 8.22, где N=M=S, a k=2), то получающаяся треугольная матрица R имеет следующую структуру:
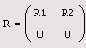
где R1 — верхняя треугольная матрица, a R2 — просто некоторая матрица, а нули обозначают, в общем случае, нулевые матрицы соответствующих размеров.
Если система вырожденная, то она имеет бесконечное множество псевдорешений (векторов, минимизирующих норму невязки). При помощи QR-разложения можно сразу выписать одно из них (правда, не обладающее минимальной нормой). В нашем примере последняя строка матрицы R содержит одни нули, поэтому последняя компонента вектора псевдорешения х может быть абсолютно любой. Если положить х2=0, то остальные компоненты х определятся из треугольной СЛАУ R1x=QTb, как это проиллюстрировано листингом 8.23.
Поиск одного из псевдорешений
Листинг 8.23. Поиск одного из псевдорешений вырожденной СЛАУ посредством QR-разложения (продолжение листинга 8.22 )
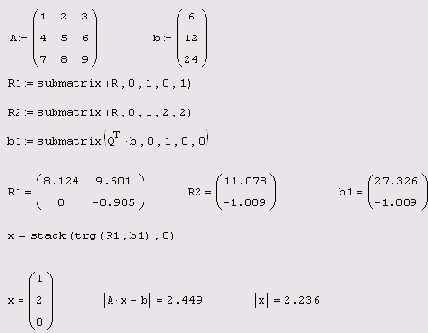
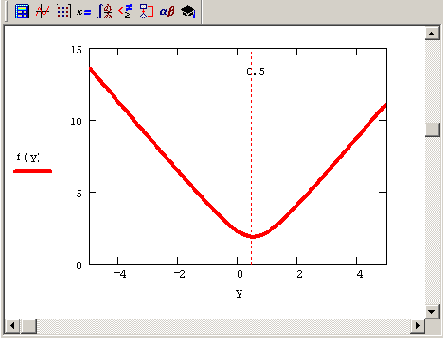
Для того чтобы выбрать из всего множества псевдорешений (минимизирующих невязку исходной СЛАУ) нормальное псевдорешение (т. е. обладающее минимальной нормой), необходимо решить соответствующую задачу минимизации (см. разд. 8.2.3). Если построено QR-разложение, сделать это намного легче. Если произвольную компоненту решения обозначить переменной у: х2=у, то она определится из соответствующей задачи оптимизации (листинг 8.24, 1—3 строки), а остальные составляющие самого решения х — из треугольной СЛАУ R1x=QTb-R2y. В последней строке листинга выводится полученное нормальное псевдорешение, а также его норма и соответствующая норма невязки (которые полезно сравнить с результатом прошлого листинга). Вспомогательный Рисунок 8.13 помогает понять структуру минимизируемой функции из листинга 8.24.
Нормальное псевдорешение
Листинг 8.24. Нормальное псевдорешение вырожденной СЛАУ (продолжение листингов 8.22 и 8.23)

Сингулярное разложение сингулярной матрицы
Листинг 8.25. Сингулярное разложение сингулярной матрицы

Венцом современных алгоритмов решения произвольных СЛАУ является SVD-разложение. Прежде чем прокомментировать соответствующий алгоритм, приведенный в листинге 8.26, обратим внимание на матрицу S, которая имеет блочную структуру. Согласно формуле (8.5), из матрицы s можно выделить подматрицу w с ненулевыми диагональными элементами. Дальнейшая последовательность действий по построению нормального псевдорешения выглядит так:
1. Нахождение единственного решения вспомогательной СЛАУ: Wy=UTb (первые два элементы вектора у во второй строке листинга 8.26, которая учитывает диагональность матрицы S).
2. Дополнение вектора нулевыми элементами до размера искомого вектора х.
3. Вычисление х простым умножением x=Vy (третья строка листинга).
Полученный результат (искомый вектор х и промежуточный у) выведен в конце листинга 8.26. Как вы можете убедиться, он совпадает с ответом, полученным в листинге 8.24 (см. предыдущий разд.) при помощи QR-разложения.
Решение вырожденной
Листинг 8.26. Решение вырожденной СЛАУ при помощи сингулярного разложения (продолжение листинга 8.25)
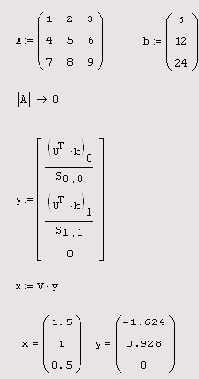
Собственные векторы
Листинг 8.27. Собственные векторы и собственные значения матрицы

Помимо рассмотренной проблемы поиска собственных векторов и значений иногда рассматривают более общую задачу, называемую задачей на обобщенные собственные значения: Ах=?Bх. В ее формулировке помимо матрицы А присутствует еще одна квадратная матрица в. Для задачи на обобщенные собственные значения имеются еще две встроенные функции, действие которых аналогично рассмотренным (листинг 8.28):
genvais (А,В) — вычисляет вектор v собственных значений, каждый из которых удовлетворяет задаче на обобщенные собственные значения; genvecs (А, B) — вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям в векторе v, который вычисляется с помощью genvals. В этой матрице i-й столбец является собственным вектором х, удовлетворяющим задаче на обобщенные собственные значения:
А, B — квадратные матрицы.
Поиск обобщенных
Листинг 8.28. Поиск обобщенных собственных векторов и собственных значений
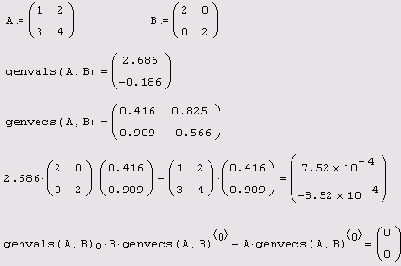
Матричные разложения
8.3. Матричные разложения
Современная вычислительная линейная алгебра — бурно развивающаяся наука. Главная проблема линейной алгебры — это решение систем линейных уравнений. В настоящее время разработано множество методов, упрощающих эти задачи, которые, в частности, зависят от структуры матрицы СЛАУ. Большинство методов основано на представлении матрицы в виде произведения других матриц специального вида, или матричных разложениях (или, по-другому, факторизация*). Как правило, после определенного разложения матрицы задача решения СЛАУ существенно упрощается. Кроме того, прибегая к определенным разложениям матриц, можно получить универсальный вид решения, как для "хороших" (см. разд. 8.1), так и для "плохих" (см. разд. 8.2) СЛАУ.
В Mathcad имеется несколько встроенных функций, реализующих алгоритмы наиболее популярных матричных разложений; и мы рассмотрим их вместе с соответствующими типовыми задачами решения СЛАУ. Однако вначале сделаем некоторые важные замечания о решении систем с треугольной матрицей.
Норма псевдорешения в зависимости
Рисунок 8.13. Норма псевдорешения в зависимости от у (продолжение листинга 8.24)
Резюмируя практические аспекты применения QR-разложения, надо отметить, что алгоритмы решения СЛАУ на его основе практически одинаковы как для хорошо обусловленных, так и для сингулярных систем.
Примечание 1
Примечание 1
На прилагаемом к книге компакт-диске вы найдете дополнительные примеры построения QR-разложения как для квадратной, так и прямоугольной матрицы А.
Произвольные системы линейных уравнений
8.2. Произвольные системы линейных уравнений
Классические задачи решения СЛАУ, рассмотренные в предыдущем разделе, предполагают равное количество уравнений и неизвестных, т. е. квадратную матрицу А. Именно для таких систем доказано, что решение существует и единственно, если определитель матрицы |А| #0. Рассмотрим теперь задачи, в которых матрица А не является квадратной либо плохо обусловлена. Разберемся в этом разделе лишь с основными свойствами и идеологией подхода к таким системам, имея в виду, что наиболее эффективными способами их решения являются матричные разложения (см. разд. 8.3).
Регуляризованное решение в зависимости
Рисунок 8.12. Регуляризованное решение в зависимости от ? (продолжение листинга 8.15)

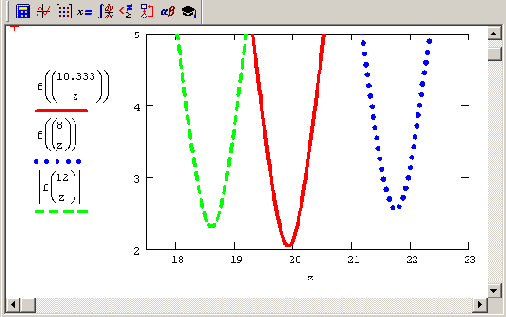
Сечения графика невязки f (х)
Рисунок 8.2. Сечения графика невязки f (х) для трех фиксированных значений х0
Системы линейных уравнений
Системы линейных уравнений
Одной из центральных проблем вычислительной линейной алгебры является решение систем линейных уравнений (см. разд. 8.1 и 8.2), отыскание собственных векторов и собственных значений (см. разд. 8.4), а также различные матричные разложения (см. разд. 8.3). Все они будут рассмотрены в данной главе, являющейся, фактически, продолжением предыдущей (которая была посвящена простейшим матричным вычислениям).
Примечание 1
Примечание 1
К системам линейных уравнений сводится множество, если не сказать большинство, задач вычислительной математики. Один из таких примеров подробно рассмотрен в разд. 10.4.
Задачу решения систем линейных алгебраических уравнений (СЛАУ), т. е. систем N уравнений вида
ai1x1+ai2x2+.. .+aiNxN=bi (8.1)
можно записать в эквивалентной матричной форме:
Аx=b, (8.2)
где А — матрица коэффициентов СЛАУ размерности NxN; х — вектор неизвестных; b — вектор правых частей уравнений. Из общего курса линейной алгебры известно, что такая СЛАУ имеет единственное решение, если матрица А является невырожденной или, по-другому, несингулярной, т. е. ее определитель не равен нулю. Самый простой способ решения почти всякой несингулярной системы — использование алгоритма Гаусса, реализованного во встроенной функции isoive (см. разд. 8.1.2).
Примечание 2
Примечание 2
На практике, в основном при решении обратных задач (inverse problems), часто приходится сталкиваться не только со СЛАУ с квадратной матрицей А, но и с прямоугольной матрицей размера MxN, т. е. системами, в которых число неизвестных не равно числу уравнений (как больше, так и меньше него). Такие системы требуют специфического подхода, который будет рассмотрен в разд. 8.2 и 8.3.
Собственные векторы и собственные значения матриц
8.4. Собственные векторы и собственные значения матриц
Завершим главу, посвященную решению СЛАУ, еще одной задачей вычислительной линейной алгебры — задачей отыскания собственных векторов х и собственных значений А, матрицы А, т. е. решения матричного уравнения Ах=?х. Такое уравнение имеет решения в виде собственных значений ?1,?2, ... и соответствующих им собственных векторов x1,x2,... Для решения таких задач на собственные векторы и собственные значения в Mathcad встроено несколько функций, реализующих довольно сложные вычислительные алгоритмы:
eigenvais (A) — вычисляет вектор, элементами которого являются собственные значения матрицы А; eigenvecs (A) — вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям матрицы А. n-й столбец вычисляемой матрицы соответствует собственному вектору n-го собственного Значения, вычисляемого eigenvais; eigenvec(A,?) — вычисляет собственный вектор для матрицы А и заданного собственного значения А.:
А — квадратная матрица.
Применение этих функций иллюстрирует листинг 8.27. В его конце приведена проверка правильности нахождения первого из собственных векторов и собственных значений, причем подстановка результата в выражение Аx=?x
проведена дважды — сначала на числовых значениях х и ?, а потом путем перемножения соответствующих матричных компонентов.
Зависимость невязки регупяризованного
Рисунок 8.11. Зависимость невязки регупяризованного решения вырожденной СЛАУ от параметра А. (продолжение листинга 8.15)
Примечание 6
Примечание 6
Любопытно также применить вместо формулы (8.3) в качестве функционала Тихонова другую зависимость: ?(х,?) = |Ах-b|+?|х-х0 |. Соответствующий пример расчетов вы найдете на компакт-диске.