Математические задачи в пакете MathCAD 12
Глава 2.1. Операторы
Каждый оператор в Mathcad обозначает некоторое математическое действие в виде символа. В полном согласии с терминологией, принятой в математике, ряд действий (например, сложение, деление, транспонирование матрицы и т. п.) реализован в Mathcad в виде встроенных операторов, а другие действия (например, sin, erf и т. п.) — в виде встроенных функций. Каждый оператор действует на одно или два числа (переменную или функцию), которые называют операндами. Если в момент вставки оператора одного или обоих операндов не хватает, то недостающие операнды будут отображены в виде местозаполнителей. Символ любого оператора в нужное место документа вводится одним из двух основных способов:
нажатием соответствующей клавиши (или сочетания клавиш) на клавиатуре; нажатием указателем мыши соответствующей кнопки на одной из математических панелей инструментов.
Напомним, что большинство математических панелей содержат сгруппированные по смыслу математические операторы, а вызвать эти панели на экран можно нажатием соответствующей кнопки на панели
Math (Математика).
ПРИМЕЧАНИЕ
Везде в этом разделе будем рассматривать только второй способ вставки оператора. Те же, кто предпочитает использовать клавиатуру, найдут перечень горячих клавиш в приложении 2.
Выше мы рассмотрели особенности применения трех операторов: присваивания (см. разд. 1.2.3), численного и символьного вывода (см. разд. 1.2.3). Разберем в данном разделе более подробно действие этих и других операторов Mathcad.
Глава 2.1.1. Арифметические операторы
Операторы, обозначающие основные арифметические действия, вводятся с
панели Calculator (Калькулятор), показанной на рис. 2.1:
сложение и вычитание: + / —; умножение и деление: • / * ; факториал: !; модуль числа: |х|; квадратный корень; корень n-й степени: , возведение х в степень у: ху ; изменение приоритета: скобки; численный вывод: = (все листинги).

Рис. 2.1. Панель Calculator
Глава 2.1.2. Вычислительные операторы
Вычислительные операторы вставляются в документы при помощи панели инструментов
Calculus (Вычисления) (рис. 2.2). При нажатии любой из кнопок в документе появляется символ соответствующего математического действия, снабженный несколькими местозаполнителями. Количество и расположение местозаполнителей определяется типом оператора и в точности соответствует их общепринятой математической записи. Например, при вставке оператора суммы (рис. 2.2) необходимо задать четыре величины: переменную, по которой надо произвести суммирование, нижний и верхний пределы, а также само выражение, которое будет стоять под знаком суммы. Для того чтобы вычислить неопределенный интеграл, следует заполнить два местозаполнителя: подынтегрального выражения и переменной интегрирования и т. д.
После ввода какого-либо вычислительного оператора имеется возможность вычислить его значение либо численно, нажатием клавиши <=>, либо аналитически, с помощью оператора символьного вывода.
ПРИМЕЧАНИЕ
Дифференцированию и интегрированию, как более сложным операциям, посвящены отдельные главы этой книги (см. гл. 3 и 4 соответственно). Суммирование и вычисление предела рассматривается ниже в этой главе (см. соответственно разд. 2.3.8 и 2.3.11).

Рис. 2.2. Вставка оператора суммирования
Глава 2.1.3. Логические операторы
Результатом действия логических, или булевых, операторов являются только числа 1 (если логическое выражение, записанное с их помощью, истинно) или 0 (если логическое выражение ложно). Чтобы вычислить значение логического выражения, например 1=1 (рис. 2.3):
1. Вставьте с панели Boolean (Булевы операторы) соответствующий оператор =.
2. В появившиеся местозаполнители вставьте операнды (две единицы).
3. Нажмите клавишу <=>, чтобы получить ответ.

Рис. 2.3. Вставка логического оператора
Получается абсурдное на первый взгляд выражение 1=1. Однако на самом деле все правильно. Слева от оператора вывода записано логическое выражение 1=1 (обратите внимание, что логический знак равенства выглядит по-другому, нежели обычный), которое является истинным. Поэтому значение данного выражения равно 1, что и показано справа от знака равенства.
Перечислим логические операторы:
больше (Greater Than) x>y; меньше (Less Than) x<y; больше или равно (Greater Than or Equal) x>_y; меньше или равно (Less Than or Equal) x_<y; равно (Equal) x=y; не равно (Not Equal to); и (And) х^у; или (Or) xvy; исключающее или (Exclusive or) x®y; отрицание (Not).
ПРИМЕЧАНИЕ
Операнды в логических выражениях могут быть любыми числами. Однако если оператор по смыслу применим только к о и 1, то любое неравное нулю число по умолчанию принимается равным 1. Но в результате все равно может получиться либо 0, либо 1. Например,
-,(-0.33)=0.
Примеры действия логических операторов приведены в листингах 2.1 и 2.2. ПРИМЕЧАНИЕ
Логические операторы чрезвычайно важны при записи в редакторе Mathcad подлежащих решению алгебраических уравнений и неравенств (см. гл. 5).
Листинг 2.1. Операторы сравнения
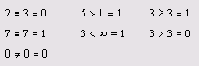
Листинг 2.1.
Булевы операторы

Глава 2.1.4. Матричные операторы
Матричные операторы предназначены для совершения различных действий над векторами и матрицами. Поскольку большинство из них реализует численные алгоритмы, о них будет подробно рассказано в разделах, посвященных линейной алгебре (см. главу 7). Остановимся в данном разделе лишь на вопросе вставки матриц в документы Mathcad.
Самый простой и наглядный способ создания вектора или матрицы заключается в следующем:
1. Нажмите кнопку Matrix or Vector (Матрица или вектор) на панели Matrix (Матрица), либо клавиши <Ctrl>+<M>, либо выберите пункт меню Insert / Matrix
(Вставка / Матрица).
2. В диалоговом окне Insert Matrix (Вставка матрицы) (рис. 2.4) задайте целое число столбцов и строк матрицы, которую хотите создать. Например, для создания вектора 3xi введите показанные на рис. 2.4 значения.
3. Нажмите кнопку ОК или Insert (Вставить) — в результате в документ будет вставлена заготовка матрицы с определенным числом строк и столбцов (рис. 2.5).
4. Введите значения в местозаполнители элементов матрицы. Переходить от одного элемента матрицы к другому можно с помощью указателя мыши либо клавиш со стрелками.

Рис. 2.4. Создание матрицы

Рис. 2.5. Результат создания матрицы
Добавление в уже созданную матрицу строк или столбцов производится точно так же:
1. Выделите линиями ввода элемент матрицы, правее и ниже которого будет осуществлена вставка столбцов и (или) строк.
2. Вставьте в него матрицу, как было описано выше. При этом допускается задание числа столбцов или строк равным нулю.
3. Заполните местозаполнители недостающих элементов матрицы.
ПРИМЕЧАНИЕ
Определить новую матрицу можно и по-другому, например (впервые в документе), присвоив определенное значение ее некоторому элементу, например,
А3,3:=1, либо импортировав в матрицу данные из внешнего файла (см. раза. 73.3).
Глава 2.1.5. Операторы выражения
Вычислительные операторы сгруппированы на панели Evaluation (Вычисления) (см. разд. 1.2.1). Перечислим их еще раз (без дополнительных комментариев):
Численный вывод (Evaluate Numerically) = ; Символьный (аналитический) вывод (Evaluate Symbolically) -> ; Присваивание (Definition) := ; Глобальное присваивание (Global Definition).
Глава 2.2. Функции
Mathcad содержит огромное количество встроенных функций. Некоторые из них просто рассчитывают определенное значение, а некоторые реализуют сложные численные алгоритмы. Учитывая, что большинство стандартных алгебраических функций Mathcad имеют общепринятую математическую форму, мы не станем приводить в данной главе все имеющиеся встроенные функции, а лишь перечислим их основные типы и приведем несколько характерных примеров, ограничившись минимальными комментариями. Полный перечень встроенных функций вы найдете в конце книги (см. приложение 3).
ПРИМЕЧАНИЕ
Напомним также (см. гл. 1), что вставлять в документ не очень знакомую функцию легче всего, пользуясь диалоговым окном
Insert Function (Вставить функцию), которое вызывается нажатием кнопки с надписью f(x) на стандартной панели инструментов. В этом диалоге функции разбиты на несколько групп, поэтому несложно выбрать из них нужную. При выделении какой-либо группы в левом списке упомянутого диалога справа обнаруживается список функций, принадлежащих этой группе. Названия групп функций, появляющихся в левом списке диалогового окна
Insert Function, приведены в скобках после названия каждого раздела этой главы.
Глава 2.2.1. Элементарные функции
Перечислим хорошо известные группы стандатртных функций (примеры некоторых из них приведены на рис. 2.6—2.8).
Exponential and logarithmic functions (Логарифмы и экспонента) (рис. 2.6). Complex (Комплексные) (листинг 2.3). Trigonometric (Тригонометрические) (листинги 2.4 и 2.5). Inverse trig (Обратные тригонометрические) (листинги 2.4 и 2.5). Hyperbolic (Гиперболические) (листинг 2.6 и рис. 2.7). Inverse hyperbolic (Обратные гиперболические). Sine (Sine-функция) (рис. 2.8).
ПРИМЕЧАНИЕ
Sine-функция появилась в версии Mathcad 11.

Рис. 2.6. Логарифмические функции

Рис. 2.7. Основные гиперболические функции

Рис. 2.8. Sine-функция
Листинг 2.3. Некоторые функции работы с комплексными числами

Листинг
2.4. Примеры тригонометрических функций

Листинг 2.5. Примеры расчета угла между прямой и осью
OX

Листинг 2.6. Пример гиперболических функций

Глава 2.2.2. Вспомогательные функции
Кроме перечисленных, Mathcad включает целый ряд вспомогательных функций, во множестве ситуаций облегчающих вычисления.
Discontinuous functions (Разрывные функции). Round-off and truncation (Сокращения и округления) (листинг 2.7). Sorting (Сортировки). Strings (Строковые). Finance functions (Финансовые). Coordinate transform (Преобразования координат) (листинг 2.8). Conditional (Условия) (листинг 2.9). Expression type (Типа выражения).
Листинг 2.7. Функции сокращения и округления

ПРИМЕЧАНИЕ
В прежних версиях Mathcad (вплоть до 11-й включительно) функции округления и сокращения могли выдавать результат, отличный от аналитического (что было связано с принципом представления чисел). В Mathcad 12 эти функции работают более правильно, выводя точный результат округления, совпадающий с символьным.
Листинг 2.8. Функции преобразования координат на плоскости

Листинг 2.9. Функции знака и условия

ПРИМЕЧАНИЕ
Разработчики Mathcad 12 восстановили встроенную функцию until, которая вплоть до 2000-й версии служила для включения в документы циклов без помощи программирования. Функция until (x, у) служит для "непрограммной" имитации цикла: если х<0, происходит вычисление очередного у, затем опять вычисляется новое
х (так или иначе зависящего от у), снова проверяется условие х<0
и т. д. Финальное значение у, при котором х становится неотрицательным, выдается в качестве результата функции.

Рис. 2.9. Функции Хевисайда и устаревшая функция Кронекера
ВНИМАНИЕ!
Начиная с Mathcad 12 функция (символ) Кронекера 5 (рис. 2.9) изъята из списка встроенных функций.
Глава 2.2.3. Функция вывода текущего времени
В версии Mathcad 12 появилась новая встроенная функция, которая иногда может быть очень полезной для хронометрирования процесса вычислений.
time (х) — значение системной переменной текущего времени (в секундах):
х — аргумент (нужен лишь для идентификации встроенной функции и не оказывает никакого влияния на результат).
Типичное использование функции требует ее двукратного вычисления: до и после расчетного фрагмента, который вы собираетесь хронометрировать (листинг 2.10). Одиночное вычисление time(x) выдает абсолютное значение системной переменной времени (первая строка листинга 2.10). Помните о том, что для получения значимой информации о времени расчетов необходимо пересчитать заново содержимое всего документа командой Tools / Calculate Worksheet (Сервис / Вычислить все).
Листинг 2.10. Хронометрирование вычислений

Глава 2.2.4. Спецфункции
В Mathcad встроено множество самых различных математических функций, которое пополняется от версии к версии. Большинство из них рассчитываются без привлечения специальных численных методов, но, тем не менее, играют важную роль, главным образом, в математической физике. Например, функции Бесселя по определению являются решениями различных краевых задач для некоторых обыкновенных дифференциальных уравнений (ОДУ). Конкретный вид соответствующих дифференциальных уравнений можно без труда отыскать в справочниках по спецфункциям или в справочной системе Mathcad.
Спецфункции в Mathcad разбиты на несколько групп:
Bessel (Функции Бесселя) (рис. 2.10 и 2.11); Error function and complementary error function (Интегралы ошибок); Special functions(Остальные спецфункции).
ПРИМЕЧАНИЕ
В Mathcad 12 появилась новая нормированная форма спецфункций Эйри (рис. 2.11), относящихся к классу бесселевых, запись которых сопровождается нижним индексом
sc (например, AiSc), улучшающая точность их вычисления при больших значениях аргумента. Другие нормированные функции Бесселя были добавлены в предыдущих версиях, в частности, Mathcad 11.

Рис. 2.10. Функции Бесселя первого рода

Рис. 2.11. Функции Эйри (Aisc появилась в Mathcad 12)
Глава 2.3. Алгебраические преобразования
В этом разделе речь пойдет об алгебраических вычислениях, которые выполняются в Mathcad, главным образом, аналитически. Как ни странно, многие пользователи Mathcad не очень хорошо осведомлены об этих возможностях, тогда как они во многих ситуациях могут существенно сэкономить их время и силы по выполнению несложных, но рутинных преобразований.
Глава 2.3.1.О способах символьных вычислений
Символьные вычисления в Mathcad можно осуществлять в двух различных вариантах:
с помощью команд меню; с помощью оператора символьного вывода —>, ключевых слов символьного процессора и обычных формул (в справочной системе Mathcad этот способ называется символьными вычислениями в реальном времени — live symbolic evaluation).
Первый способ более удобен, когда требуется быстро получить какой-либо аналитический результат для однократного использования, не сохраняя сам ход вычислений. Второй способ более нагляден, т. к. позволяет записывать выражения в традиционной математической форме и сохранять символьные вычисления в документах Mathcad. Кроме того, аналитические преобразования, проводимые через меню, касаются только одного, выделенного в данный момент, выражения.
ПРИМЕЧАНИЕ
В символьных вычислениях допускается использование большинства встроенных функций Mathcad, конечно, за исключением тех, которые реализуют численные методы.
Символьный процессор Mathcad умеет выполнять основные алгебраические преобразования, такие как упрощение выражений, разложение их на множители, символьное суммирование и перемножение.
Для символьных вычислений при помощи команд предназначено главное меню Symbolics (Символика), объединяющее математические операции, которые Mathcad умеет выполнять аналитически. Для реализации второго способа применяются все средства Mathcad, пригодные для численных вычислений (например, панели Calculator, Evaluation и т. д.), и специальная математическая панель инструментов, которую можно вызвать на экран нажатием кнопки
Symbolic Keyword Toolbar (Панель символики) на панели Math (Математика). На панели
Symbolic (Символика) находятся кнопки, соответствующие специфическим командам символьных преобразований
(рис. 2.12). Например, таким как разложение выражения на множители, приведение подобных слагаемых и другим операциям, которые в Mathcad нельзя проводить численно, и для которых, соответственно, не предусмотрены встроенные функции.
ПРИМЕЧАНИЕ
Необходимо отметить, что приемы более сложных символьных вычислений описываются также в остальных главах данной книги, в рамках рассказа о решении конкретных вычислительных задач.

Рис. 2.12. Панель Symbolic
Глава 2.3.2. Разложение выражений
Рассмотрим оба типа символьных вычислений на простом примере разложения на сомножители выражения
cos (4х). В ходе операции символьного разложения, или расширения, раскрываются все суммы и произведения, а сложные тригонометрические зависимости разлагаются с помощью тригонометрических тождеств. Разложение выражений производится путем выбора команды
Symbolics / Expand (Символика / Разложить) либо использованием вместе с оператором символьного вывода ключевого слова
expand.
Первый способ (разложение с помощью меню)
1. Введите выражение cos (4х).
2. Выделите его целиком (см. рис. 2.13).
3. Выберите в главном меню пункты Symbolics / Expand (Символика / Разложить).
После этого результат разложения выражения появится чуть ниже в виде еще одной строки (рис. 2.13).

Рис. 2.13. Разложение выражения на множители при помощи команды меню Symbolics / Expand

Рис. 2.14. Символьное разложение части выражения и его результат
ВНИМАНИЕ!
Символьные операции с помощью меню возможны лишь над каким-либо объектом (выражением, его частью или отдельной переменной). Для того чтобы правильно осуществить желаемое аналитическое преобразование, предварительно необходимо выделить тот объект, к которому оно будет относиться. В данном случае преобразование было применено ко всему выражению cos (4-х). Если же выделить часть формулы, как показано на рис. 2.14, то соответствующее преобразование будет отнесено только к выделенной части (нижняя строка на этом рисунке).
Второй способ (разложение с помощью оператора ->).
1. Введите выражение, например cos (4х).
2. Нажмите кнопку Expand (Разложить) на панели Symbolic (Символика).

Рис. 2.15. Символьное разложение выражения
3. Введите в местозаполнитель после появившегося ключевого слова expand (рис. 2.15, сверху) имя переменной х либо нажмите клавишу <Del>, чтобы просто удалить местозаполнитель.
4. Введите оператор символьного вывода —>.
5. Нажмите клавишу <Enter> либо просто щелкните мышью за пределами выражения.
ПРИМЕЧАНИЕ
Можно действовать и в другом порядке: сначала ввести ключевое слово, а уже затем впечатать появившиеся местозаполнители выражение и переменную (рис. 2.16).

Рис. 2.16. Результат первоначального ввода ключевого слова
Оператор символьного вывода, как вы помните, можно ввести в редакторе Mathcad несколькими способами: нажатием кнопки —> на любой из панелей
Evaluation (Выражения) или Symbolic (Символика) либо сочетанием клавиш <Ctrl>+<.>. Результат символьного разложения выражения показан на рис. 2.15, снизу.
СОВЕТ
Если вы можете выбрать способ символьных вычислений, рекомендую второй путь — с помощью оператора -», поскольку при этом в документе сохраняются действия пользователя. Наличие специального меню символьных вычислений — своего рода дань очень давним версиям Mathcad. В них аналитические преобразования были встроены не так гармонично и были доступны, главным образом, через меню.
Не всякое выражение поддается аналитическим преобразованиям. Если это так (либо в силу того, что задача вовсе не имеет аналитического решения, либо она оказывается слишком сложной для символьного процессора Mathcad), то в качестве результата выводится само выражение (листинг 2.11, внизу).
Листинг 2.11. Символьные преобразования

ПРИМЕЧАНИЕ
Далее в этой главе, рассматривая символьные вычисления с помощью меню, будем иллюстрировать результаты рисунками, а символьные вычисления с применением оператора -> приводить в виде листингов.
Глава 2.3.3. Упрощение выражений
Упрощение выражений — очень часто применяемая операция, противоположная по смыслу операции разложения, рассмотренной в предыдущем разделе. Символьный процессор Mathcad стремится так преобразовать выражение, чтобы оно приобрело более простую форму. При этом используются различные арифметические формулы, приведение подобных слагаемых, тригонометрические тождества, пересчет обратных функций и др. Чтобы упростить выражение с помощью меню (рис. 2.17):
1. Введите выражение.
2. Выделите выражение целиком или его часть, которую нужно упростить.
3. Выберите команду Symbolics / Simplify (Символика / Упростить).

Рис. 2.17. Упрощение выражения
Для упрощения выражения при помощи оператора символьного вывода используйте ключевое слово
simplify (листинг 2.12). Не забывайте, если некоторым переменным, входящим в выражение, ранее были присвоены некоторые значения, то они будут подставлены в него при выполнении символьного вывода (листинг 2.13).
Листинг 2.12. Упрощение выражения

Листинг 2.13. Упрощение выражения с подстановкой значения переменных

Упрощение выражений, содержащих числа, производится по-разному, в зависимости от наличия в числах десятичной точки. Если она есть, то выполняется непосредственное вычисление выражения (листинг 2.14).
Листинг 2.14. Упрощение выражения с числами

Глава 2.3.4. Разложение на множители
Разложение выражений на простые множители производится при помощи команды Symbolics/ Factor (Символика/ Разложить на множители) (рис. 2.18) либо использованием вместе с оператором символьного вывода ключевого слова
factor (листинг 2.15). Эта операция позволяет разложить полиномы на произведение более простых полиномов, а целые числа — на простые сомножители. Применяя команду меню, не забывайте перед ее вызовом выделить все выражение или его часть, которую планируете разложить на множители.
Листинг 2.15. Примеры разложения на множители


Рис. 2.18. Разложение выражения на множители
Глава 2.3.5. Приведение подобных слагаемых
Чтобы привести подобные слагаемые полинома с помощью меню (рис. 2.19):
1. Введите выражение.
2. Выделите в выражении имя переменной, относительно которой надо привести подобные слагаемые (в примере на рис. 2.19 это переменная у).
3. Выберите команду Symbolics / Collect (Символика / Привести подобные).
В результате появится строка с результатом приведения подобных слагаемых (нижняя строка на рис. 2.19).
Чтобы привести подобные слагаемые с помощью оператора символьного вывода (листинг 2.16):
1. Введите выражение.
2. Нажмите кнопку Collect на панели Symbolic (Символика).
3. Введите в местозаполнитель после вставленного ключевого слова collect имя переменной, относительно которой требуется привести подобные слагаемые (в первой строке примера из листинга 2.16 это переменная х, во второй — у).
4. Введите оператор символьного вывода —>.
5. Нажмите клавишу <Enter>.
ПРИМЕЧАНИЕ
После ключевого слова collect допускается задание нескольких переменных через запятую. В этом случае, что иллюстрируется последней строкой листинга 2.6, приведение подобных слагаемых выполняется последовательно по всем переменным.

Рис. 2.19. Приведение подобных слагаемых
Листинг 2.16. Приведение подобных слагаемых по разным переменным

Глава 2.3.6. Вычисление коэффициентов полинома
Если выражение является полиномом относительно некоторой переменной х, заданным не в обычном виде
a0+a1x+a2x2+..., а как произведение других, более простых полиномов, то коэффициенты
a0,a1,a2... легко определяются символьным процессором Mathcad. Коэффициенты сами могут быть функциями (подчас довольно сложными) других переменных.
Чтобы вычислить полиномиальные коэффициенты в выражении при помощи меню (рис. 2.20):
1. Введите выражение.
2. Выделите в нем имя переменной или выражение, для которого требуется рассчитать полиномиальные коэффициенты (в примере на рис. 2.20 это переменная z).
3. Выполните команду Symbolic / Polynomial Coefficients (Символика / Коэффициенты полинома).
В результате под выражением появится вектор, состоящий из полиномиальных коэффициентов. Первым элементом вектора является свободный член а0, вторым —
ai и т. д.

Рис. 2.20. Вычисление коэффициентов полинома
ПРИМЕЧАНИЕ
Конкретная задача, требующая вычисления полиномиальных коэффициентов, приведена в разделе, посвященном численному отделению корней полинома (см. разд. 5.2,3).
Чтобы вычислить полиномиальные коэффициенты с помощью оператора символьного вывода:
1. Введите выражение.
2. Нажмите кнопку Coeffs на панели Symbolic (Символика).
3. Введите в местозаполнитель после вставленного ключевого слова coeffs аргумент полинома.
4. Введите оператор символьного вывода —>.
5. Нажмите клавишу <Enter>.
Примеры вычисления коэффициентов полинома приведены в листингах 2.17 и 2.18. Листинг 2.17 показывает расчет коэффициентов для разных аргументов. Второй листинг демонстрирует возможность определения коэффициентов не только для отдельных переменных, но для более сложных выражений, входящих в рассматриваемую формулу в качестве составной части.
Листинг 2.17. Вычисление коэффициентов полинома
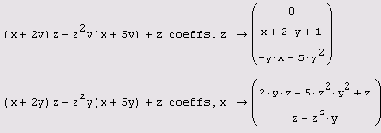
Листинг 2.18.
Вычисление полиномальных коэффициентов для простой переменной и выражения

Глава 2.3.7. Разложение на простые дроби
Чтобы разложить сложную дробь на более простые дроби, следует либо выполнить команду
Symbolics / Variable / Convert to Partial Fractions
(Символика / Переменная / Разложить на элементарные дроби) (рис. 2.21),
либо указать ключевое слово parfrас (листинг 2.19). Применяя первый способ (меню), не забывайте перед выбором его команды выделить переменную, по которой будет производиться разложение, а если используется второй способ (с оператором символьного вывода), то имя переменной следует указать после ключевого слова
parfrac. В общем, последовательность действий при разложении на дроби та же самая, что и обычно (см., например, разд. 2.3.4).

Рис. 2.21. Разложение сложной дроби на элементарные дроби
Листинг 2.19. Разложение на элементарные дроби

Глава 2.3.8. Вычисление рядов и произведений
Чтобы вычислить аналитически конечную или бесконечную сумму или произведение:
1. Введите выражение, используя панель Calculus (Вычисления) для вставки соответствующих символов суммирования или произведения. При необходимости введите в качестве предела ряда символ бесконечности (клавиши <Ctrl>+<Shift>+<Z>).
2. В зависимости от желаемого стиля символьных вычислений выберите команду Symbolics / Simplify (Символика / Упростить) или введите оператор символьного вывода —>.
Примеры численного и символьного вычисления рядов и произведений приведены в листингах 2.20 и 2.21.
Листинг 2.20. Символьные и численные расчеты рядов

Листинг 2.21.
Символьный расчет произведения

Глава 2.3.9. Подстановка переменной
Очень удобная возможность символьных вычислений — это операция подстановки значения переменной в выражение. При помощи меню подстановка производится следующим образом (рис. 2.22):
1. Выделите значение переменной, которое необходимо подставить в некоторое выражение. Значение переменной может быть любым выражением относительно любых переменных (на рис. 2.22 в качестве подстановки взята самая первая строка документа).
2. Скопируйте значение переменной в буфер обмена, например, нажатием клавиш <Ctrl>+<C> или кнопки Сору (Копировать) на панели инструментов
Standard (Стандартная).
3. Выделите в выражении, в которое требуется подставить значение из буфера обмена, переменную, которая будет заменяться (во второй строке на рис. 2.22 выделена переменная х).
4. Выполните команду Symbolics / Variable / Substitute (Символика / Переменная / Подставить).
Результат этих действий иллюстрируется нижней строкой в документе на рис. 2.22.

Рис. 2.22. Подстановка значения переменной
Для осуществления той же операции в совокупности с оператором символьного вывода используйте ключевое слово
substitute, которое вставляется в документ одноименной кнопкой на панели
Symbolic (Символика). После ключевого слова substitute необходимо ввести в местозаполнители логическое выражение, показывающее, какую именно переменную какой формулой следует заменить (листинг 2.22).
Листинг 2.22. Подстановка значения переменной

Глава 2.3.10. Получение численного значения выражения
С помощью символьного процессора можно рассчитать численное значение выражения (действительное или комплексное). Иногда такой путь представляется более удобным, чем применение численного процессора (т. е. знака обычного равенства). Чтобы рассчитать значение некоторого выражения (рис. 2.23), выберите команду
Symbolics / Evaluate / Symbolically (Символика / Вычислить / Символьно) либо пункт
Symbolics / Evaluate / Floating Point (Символика / Вычислить / С плавающей точкой). В последнем случае вам будет предложено с помощью диалога
Floating Point Evaluation (Вычисления с плавающей точкой) задать точность вывода. В итоге применения данных команд Mathcad заменяет символьные результаты, где это возможно, значениями в виде чисел с плавающей точкой.

Рис. 2.23. Вычисление выражения с плавающей точкой
Еще один пункт меню Symbolics / Evaluate / Complex (Символика / Вычислить / Комплексно) позволяет представить выражение в виде
a+bi.
Аналогичные по действию ключевые слова float и complex можно использовать в документах, вводя их с панели
Symbolic (Символика). Ключевое слово float применяется вместе со значением точности вывода результата с плавающей точкой (листинг 2.23). С помощью слова
complex можно преобразовывать выражения как в символьном виде, так и с учетом численных
значений, если они были ранее присвоены переменным (несколько примеров приведено в листинге 2.24).
Листинг 2.23. Вычисление выражения с плавающей точкой

Листинг 2.24.
Комплексные преобразования выражений

Глава 2.3.11. Вычисление предела
Наиболее ярким проявлением возможностей символьного процессора в Mathcad являются аналитические вычисления пределов, производных, интегралов и разложений в ряд, а также решение алгебраических уравнений. Все эти операции, при выполнении их посредством меню
Symbolics (Символика), находятся в его подменю Variable (Переменная). Соответственно, требуется предварительное выделение в выражении переменной, относительно которой будет совершаться операция. Для выделения переменной достаточно поместить ее между линиями ввода, но для большей наглядности лучше выделить ее черным цветом путем протаскивания указателя мыши через нужную часть выражения.
ПРИМЕЧАНИЕ
В отличие от других вычислительных операторов, пределы могут быть вычислены только символьно.
Пределы (листинг 2.25):
Листинг 2.25. Операторы символьного вычисления пределовдвусторонний; левый; правый.

Глава 2.3.12.О специфике аналитических вычислений
Выше в этой главе были разобраны основные приемы символьных вычислений в Mathcad. Они, как правило, были показаны на простых примерах, которые иллюстрировали ту или иную символьную операцию. Тем не менее при проведении разнообразных (и численных тоже) расчетов в Mathcad возможности символьного процессора можно использовать более эффективно. Отметим некоторые из них.
При проведении символьных вычислений с оператором символьного вывода функции пользователя и переменные, определенные ранее в документе Mathcad, воспринимаются символьным процессором корректно. Таким образом, имеется мощный аппарат включения символьных расчетов в программы пользователя. Примеры применения функции пользователя. приведены в листингах 2.26 и 2.27. Сравните последние строчки этих листингов. Несмотря на их идентичность слева от знака символьного вывода, результат получен различный. Это связано с тем, что в листинге 2.27 предварительно переменной
х присвоено значение 4. Поскольку значения переменных влияют на символьные вычисления, то результат учитывает подстановку вместо
х числа 4.
Листинг 2.26. Функция пользователя в символьных вычислениях

Листинг 2.27. Значения переменных влияют на результат символьных
вычислений

Напротив, при осуществлении символьных операций через меню Symbolics (Символика) символьный процессор "не видит" ничего, кроме выражения, в пределах которого находятся линии ввода. Поэтому ни функции пользователя, ни предварительно определенные значения каких-либо переменных никак не влияют на вычисления.
СОВЕТ
Используйте меню Symbolics (Символика), если требуется "сиюминутно" провести некоторые аналитические действия с выражением и получить ответ в общем виде, не учитывающем текущие значения переменных, входящих в выражение.