Математические задачи в пакете MathCAD 12
Глава 4.1. Определенный интеграл
Интегрирование в Mathcad реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярными. Несмотря на то, что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным.
Глава 4.1.1. Оператор интегрирования
Интегрирование, как и дифференцирование, и множество других математических действий, устроено в Mathcad по принципу "как пишется, так и вводится". Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели
Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7> (или символа "&", что то же самое). Появится символ интеграла с несколькими местозаполнителями (рис. 4.1), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.
ПРИМЕЧАНИЕ
Если пределы интегрирования имеют размерность, то она должна быть одной и той же для обоих пределов.

Рис. 4.1. Оператор интегрирования
Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором — в случае успеха будет найдено точное значение интеграла с помощью символьного процессора Mathcad. Эти два способа иллюстрирует листинг 4.1. Конечно, символьное интегрирование возможно только для сравнительно небольшого круга несложных подынтегральных функций.
Листинг 4.1. Численное и символьное вычисление определенного интеграла

ПРИМЕЧАНИЕ 1
Можно вычислять интегралы с одним или обоими бесконечными пределами (листинг 4.2). Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью
Calculus (Вычисления). Чтобы ввести (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.
Листинг 4.2. Вычисление интеграла с бесконечными пределами

ПРИМЕЧАНИЕ 2
Подынтегральная функция может зависеть от любого количества переменных. Именно для того чтобы указать, по какой переменной Mathcad следует вычислять интеграл, и нужно вводить ее имя в соответствующий местозаполнитель. Помните, что для численного интегрирования по одной из переменных предварительно следует задать значение остальных переменных, от которых зависит подынтегральная функция и для которых вы намерены вычислить интеграл (листинг 4.3).
Листинг 4.3. Интегрирование функции двух переменных по разным переменным
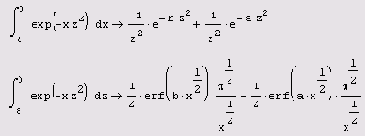

Рис. 4.2. Использование оператора интегрирования в функции пользователя
ПРИМЕЧАНИЕ 3
Оператор интегрирования может использоваться точно так же, как и другие операторы: для определения функций, в циклах и при вычислении ранжированных переменных. Пример присваивания пользовательской функции f (z) значения определенного интеграла и вычисления нескольких ее значений приведен на рис. 4.2. На том же рисунке показано, как можно построить график результата интегрирования.
Глава 4.1.2. О выборе алгоритма численного интегрирования
Результат численного интегрирования — это не точное, а приближенное значение интеграла, определенное с погрешностью, которая зависит от встроенной константы
TOL. Чем она меньше, тем с лучшей точностью будет найден интеграл, но и тем больше времени будет затрачено на расчеты. По умолчанию
TOL=0. 001. Для того чтобы ускорить вычисления, можно установить большее значение
TOL.
СОВЕТ
Если скорость расчетов имеет для вас принципиальное значение, например, при многократном вычислении интеграла внутри цикла, проявите осторожность, выбирая значение точности. Обязательно поэкспериментируйте на тестовом примере с характерной для ваших расчетов подынтегральной функцией. Посмотрите, как уменьшение константы
TOL сказывается на погрешности интегрирования, вычислив интеграл для разных ее значений и выбрав оптимальное, исходя из соотношения точность/скорость вычислений.
Отдавайте себе отчет в том, что при вводе в редакторе Mathcad оператора численного интегрирования вы фактически создаете самую настоящую программу. Например, программой является первая строка листинга с рис. 4.2, просто основная ее часть скрыта от вашего взора разработчиками компании MathSoft. В большинстве случаев об этом не приходится специально задумываться, можно полностью положиться на Mathcad. Но иногда может потребоваться умение управлять параметрами этой программы, как мы уже рассмотрели на примере выбора константы
TOL. Кроме нее, пользователь имеет возможность выбирать сам алгоритм численного интегрирования. Для этого:
1. Щелкните правой кнопкой мыши в любом месте на левой части вычисляемого интеграла.
2. В появившемся контекстном меню выберите один из имеющихся в наличии численных алгоритмов, например
Romberg (Ромберга) (рис. 4.3).
Обратите внимание, что перед тем как один из алгоритмов выбран впервые, как показано на рис. 4.3, флажок проверки в контекстном меню установлен
возле пункта AutoSelect (Автоматический выбор). Это означает, что алгоритм определяется Mathcad, исходя из анализа пределов интегрирования и особенностей подынтегральной функции. Как только один из алгоритмов выбран, этот флажок сбрасывается, а избранный алгоритм отмечается точкой.
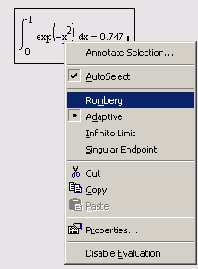
Рис. 4.3. Выбор алгоритма численного интегрирования производится при помощи контекстного меню
Разработчиками Mathcad запрограммированы четыре численных метода интегрирования:
Romberg (Ромберга) — для большинства функций, не содержащих особенностей; Adaptive (Адаптивный) — для функций, быстро меняющихся на интервале интегрирования; Infinite Limit (Бесконечный предел) — для интегралов с бесконечными пределами; Singular Endpoint (Сингулярная граница) — для интегралов с сингулярностью на конце (применяется модифицированный алгоритм Ромберга для функций, не определенных на одном или обоих концах интервала интегрирования).
Старайтесь все-таки оставить выбор численного метода за Mathcad, установив флажок
AutoSelect (Автоматический выбор) в контекстном меню. Попробовать другой метод можно, например, чтобы сравнить результаты расчетов в специфических случаях, когда у вас закрадываются сомнения в их правильности.
Если подынтегральная функция "хорошая", т. е. не меняется на интервале интегрирования слишком быстро, не имеет особенностей и не обращается в бесконечность, то численное решение интеграла не принесет никаких неприятных сюрпризов.
Глава 4.1.3.О традиционных алгоритмах интегрирования
Прежде чем перейти к изложению метода численного интегрирования, реализованного в Mathcad, скажем несколько слов об основных принципах численного интегрирования. Исходя из геометрического смысла определенного интеграла функции f (х) как площади фигуры, образованной графиком этой функции и осью
х, можно предложить самый простой способ интегрирования "хорошей" функции — применить формулу прямоугольников. С ее помощью площадь упомянутой искомой фигуры подсчитывается как сумма элементарных прямоугольников, множеством которых заменяется подынтегральная функция
f (х).
Иллюстрация метода прямоугольников приведена на рис. 4.4. Для подсчета интеграла
i интервал интегрирования [а,b] разбивается на
N отрезков. На. каждом i-м отрезке f (х) заменяется прямоугольником с шириной
h и высотой f (xi). Площадь каждого из этих элементарных прямоугольников составляет
hf (xi), а их сумма s может считаться приближением к искомому интегралу I. Несложно показать, что при N->~ множество элементарных прямоугольников стремится к искомой фигуре, образованной подынтегральной функцией, а значение
S->I, причем погрешность (отличие
s от точного значения i) составляет o(h2).
Можно воспринимать смысл алгоритма прямоугольников в замене исходной подынтегральной функции другой, близкой к ней (в данном случае, кусочно-непрерывной) функцией, интеграл от которой легко подсчитать аналитически. Принцип более точных методов интегрирования как раз и состоит в интерполяции подынтегральной функции f (х) некоторой близкой зависимостью у(х) и расчете интеграла уже от этой функции. Важно, чтобы при этом, во-первых, интеграл от у(х) мог быть точно рассчитан аналитическими методами; и, во-вторых, функция f (х) была бы по возможности ближе к у (х), чтобы уменьшить погрешность.

Рис. 4.4. Реализация алгоритма прямоугольников
Очевидно, что наиболее простой алгоритм заключается в интерполяции подынтегральной функции на каждом из
N шагов интегрирования f (х) каким-либо полиномом у(х). Известно, что могут быть предложены различные пути построения интерполирующих полиномов, отличающихся, в частности, порядком. Например, полиномы Лагранжа строятся при интерполяции
f (х) в n точках на каждом из N элементарных интервалов интегрирования. Семейство классических алгоритмов интегрирования в этом случае называется методами Ньютона—Котеса. Заметим, что при
n=1 полиномом является прямая линия, и мы имеем метод трапеций; при
n=2 интерполирующим полиномом на каждом шаге интегрирования будет квадратичная парабола, и мы получим алгоритм Симпсона и т. д.
ПРИМЕЧАНИЕ
Дополнительные сведения об алгоритме полиномиальной интерполяции приведены в
главе 13.

Рис. 4.5. Оценка погрешности алгоритма прямоугольников
Недостатком перечисленных традиционных алгоритмов являются затруднения в количественной оценке погрешности. Аналитические формулы для погрешности включают, помимо множителя ьк, задающего, собственно, порядок аппроксимации метода, сомножитель, характеризующий величину производной (определенного высшего порядка) подынтегральной функции. Оценить ее значение при конкретных расчетах очень сложно, и поэтому, соответственно, сложно вычислить суммарную погрешность алгоритма. В то
же время сведения о величине погрешности являются очень важными, и, чаще всего, желательно иметь их количественную оценку, чтобы оптимально выбрать число разбиений интервала интегрирования N.
Для апостериорной оценки погрешности можно, например, применять анализ зависимости s(N), подсчитанной для нескольких значений
N (рис. 4.5). Зная, что, с одной стороны, s(N) изменяется по определенному степенному закону N~K, и, с другой, s(N)->i (к точному значению интеграла), можно довольно точно определить погрешность метода. На нижнем графике рис. 4.5 приведена зависимость погрешности от
N (правда, в данном случае мы использовали для наглядности графика точное значение интеграла, которое в практических случаях, конечно, неизвестно). Именно с подобной процедурой и связан алгоритм расчета определенных интегралов, использованный в Mathcad, который будет представлен в следующем разделе.
Глава 4.1.4. Алгоритм Ромберга
После сделанных вводных замечаний приведем основные идеи итерационного алгоритма Ромберга, который применяется в системе Mathcad для выполнения операции численного интегрирования.
Сначала строится несколько интерполирующих полиномов, которые заменяют на интервале интегрирования подынтегральную функцию f (х). В качестве первой итерации полиномы вычисляются по 1, 2 и 4 интервалам. Например, как уже отмечалось выше, первый полином, построенный по 1 интервалу, — это просто прямая линия, проведенная через две граничные точки интервала интегрирования, второй — квадратичная парабола и т. д. Интеграл от каждого полинома с известными коэффициентами легко вычисляется аналитически. Таким образом, определяется последовательность интегралов от интерполирующих полиномов: I1,I2,I4,... Например, по правилу трапеций I1=(b-a) (f (a) +f (b)) /2 и т. д. Из-за интерполяции по разному числу точек вычисленные интегралы I1, I2, ... несколько отличаются друг от друга. Причем чем больше точек используется для интерполяции, тем интеграл от интерполяционного полинома ближе к искомому интегралу I, стремясь к нему в пределе бесконечного числа точек. Поэтому определенным образом осуществляется экстраполяция последовательности ii,i2,i4, ... до нулевой ширины элементарного интервала. Результат этой экстраполяции j принимается за приближение к вычисляемому интегралу. Осуществляется переход к новой итерации с помощью еще более частого разбиения интервала интегрирования, добавления нового члена последовательности интерполирующих полиномов и вычисления нового (N-го) приближения Ромберга JN. Чем больше количество точек интерполяции, тем ближе очередное приближение Ромберга к вычисляемому интегралу и, соответственно, тем меньше оно отличается от приближения предыдущей итерации. Как только разница между двумя последними итерациями | JN-JN-11 становится меньше погрешности TOL или меньше TOL|JN|, итерации прерываются, и JN появляется на экране в качестве результата интегрирования.
Глава 4.2. Неопределенный интеграл
Предыдущий раздел был посвящен проблеме поиска определенного интеграла, т. е. числового значения, равного площади фигуры, образованной графиком подынтегральной функции и.осью х (см. рис. 4.4). Задача нахождения неопределенного интеграла намного сложнее, поскольку связана с поиском функции, производная от которой равна исходной подынтегральной функции. Решение этой задачи целиком возложено на символьный процессор Mathcad.
Глава 4.2.1. Символьное интегрирование
Для того чтобы аналитически проинтегрировать некоторую функцию, следует ввести с панели
Calculus (Вычисления) символ неопределенного интеграла, в появившемся в документе шаблоне заполнить местозаполнители и, наконец, ввести знак символьного равенства. В случае успеха по истечении некоторого времени расчетов справа от введенного выражения появится его аналитический результат (листинг 4.4). Если же функцию не удается проинтегрировать аналитически, введенное вами выражение будет просто продублировано (листинг 4.5).
ПРИМЕЧАНИЕ
Помните, что при символьном интегрировании допускается использовать в выражениях, которые вы вводите, различные параметры. Если перед выражением вы нигде не определяли их значения, то (в случае успешных вычислений) символьный процессор Mathcad выдаст аналитическую зависимость результата интегрирования от этих параметров (как в листинге 4.4 от параметра а).
Листинг 4.4. Аналитическое вычисление неопределенного интеграла
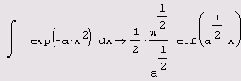
Листинг 4.5.
Аналитическое интегрирование невозможно

Глава 4.2.2. Интегрирование при помощи меню
Для вычисления неопределенного интеграла от некоторого выражения по определенной переменной при помощи меню выделите в выражении переменную и выполните команду
Symbolics / Variable / Integrate (Символика / Переменная / Интегрировать) (рис. 4.6). Вычисленное аналитическое представление неопределенного интеграла появится ниже. При этом результат может содержать как встроенные в Mathcad функции, так и другие спецфункции, которые нельзя непосредственно рассчитать в Mathcad, но символьный процессор "умеет" выдавать их в качестве результата некоторых аналитических операций.

Рис. 4.6. Интегрирование выражения по переменной при помощи меню
Глава 4.3. Интегралы специального вида
Завершим разговор о приемах интегрирования в среде Mathcad примерами вычислений в некоторых специальных случаях, которые довольно часто встречаются в самых разнообразных областях математики.
Глава 4.3.1. Интегралы с бесконечными пределами
Как мы уже говорили (см. примечание 1 в разд. 4.1.1 и листинг 4.2), для того, чтобы вычислить определенный интеграл с одним или обоими бесконечными пределами, достаточно ввести, пользуясь панелью
Calculus (Вычисления), специально предусмотренный разработчиками символ бесконечности в нужные местозаполнители интервалов интегрирования.
Глава 4.3.2. Расходящиеся интегралы
Если интеграл расходится (равен бесконечности), то вычислительный процессор Mathcad может выдать сообщение об ошибке, выделив при этом оператор интегрирования, как обычно, красным цветом. Чаще всего ошибка будет иметь тип "Found a number with a magnitude greater than
10307" (Найдено число, превышающее значение
10307) или "Can't converge to a solution"
(Не сходится к решению). Листинг 4.6 демонстрирует невозможность численного расчета интеграла
(нижняя строка листинга). Тем не
менее символьный процессор справляется с этим интегралом, совершенно правильно находя его бесконечное значение (верхняя строка листинга 4.6).
Листинг 4.6. Вычисление расходящегося интеграла

При попытке численного решения задачи листинга 4.6 методом, отличным от алгоритма вычисления интегралов с бесконечными пределами (Infinite Limit), получится неверное решение (листинг 4.7). А именно, вместо бесконечности будет выдано большое, но конечное число, немного не дотягивающее до численной бесконечности, являющейся для вычислительного
процессора просто большим числом ю307. Отметим, что Mathead в режиме автоматического выбора алгоритма (AutoSelect) предлагает для интегралов с бесконечным пределом именно алгоритм
Infinite Limit.
Листинг 4.7. Плохо выбранный численный алгоритм (
в данном случае, адаптивный) неверно находит
расходящийся интеграл

Глава 4.3.3. Интеграл с переменным пределом
Символьный процессор предоставляет замечательные возможности аналитического вычисления интегралов, в том числе зависящих от параметров. Особую важность имеет вычисление интеграла с переменным пределом (верхним или нижним), для которого один из пределов интегрирования является переменной, отличной от переменной интегрирования (листинг 4.8). Нетрудно сообразить, что, с точки зрения символьного процессора, интеграл с переменным пределом является обычным определенным интегралом, зависящим от дополнительного параметра.
Листинг 4.8. Аналитическое вычисление интеграла с переменным верхним
пределом

Глава 4.3.4. Кратные интегралы
Кратным называется интеграл функции многих переменных, берущийся по нескольким переменным. Для того чтобы вычислить кратный интеграл:
1. Введите, как обычно, оператор интегрирования.
2. В соответствующих местозаполнителях введите имя первой переменной интегрирования и пределы интегрирования по этой переменной.
3. На месте ввода подынтегральной функции введите еще один оператор интегрирования (рис. 4.7).
4. Точно так же введите вторую переменную, пределы интегрирования и подынтегральную функцию (если интеграл двукратный) или следующий оператор интегрирования (если более чем двукратный) и т. д., пока выражение с многократным интегралом не будет введено окончательно.

Рис. 4.7. Ввод нескольких операторов интегрирования для расчета кратного интеграла
Пример символьного и численного расчета двукратного интеграла в бесконечных пределах приведен в листинге 4.9. Обратите внимание, что символьный процессор "угадывает" точное значение интеграла л, а вычислительный определяет его приближенно и выдает в виде числа 3.142.
Листинг 4.9. Символьное и численное вычисления кратного интеграла

ВНИМАНИЕ!
Аккуратнее вводите в редакторе Mathcad кратные интегралы, если они имеют различные пределы интегрирования по разным переменным. Не перепутайте пределы, относящиеся к разным переменным. Если вы имеете дело с такого рода задачами, обязательно разберитесь с листингом 4.10, в котором символьный процессор вычисляет двукратный интеграл. В первой строке пределы интегрирования [а,
b] относятся к переменной у, а во второй строке— к переменной X.
Листинг 4.10. Символьное вычисление кратных интегралов

Глава 4.3.5. Пример: длина дуги кривой
В заключение приведем пример использования вычислительного процессора Mathcad для расчета длины участка кривой, задаваемой некоторой функцией f (x) в промежутке между двумя значениями ее аргумента а и ь (рис. 4.8). Решение данной простой задачи математического анализа приведено в листинге 4.11, причем формула, по которой рассчитывается длина дуги, приведена в третьей (последней) строке листинга. Обратите внимание, что для получения результата необходимо применить и операцию численного интегрирования, и дифференцирования.

Рис. 4.8. График функции определяет дугу некоторой длины (продолжение листинга 4.11)
Листинг 4.11. Расчет длины дуги кривой

Глава 4.4. Интеграл Фурье
Обратимся теперь к характерным проблемам вычислительной математики, связанным с (аналитическим или численным) вычислением интегралов определенного вида. Задачи, о которых мы собираемся рассказать, тесно связаны с алгоритмами обработки данных, поэтому содержание этого раздела будет перекликаться с материалом главы 14 (см. разд. 14.1). Благодаря обширному применению для вычисления таких интегралов разработаны специфические алгоритмы, несравненно более эффективные, чем традиционные (см. разд. 4.1.4), причем некоторые из них имеются в арсенале Mathcad в форме встроенных функций вычислительного процессора и соответствующих операций символьного процессора.
Наиболее широко распространенным интегральным преобразованием является преобразование Фурье, которое представляет функцию f (х) в виде интеграла по гармоническим функциям, называемого интегралом Фурье:
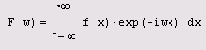
Функция F(CO) называется также преобразованием Фурье, или Фурье-спектром исходной функции f (х). Ее аргумент ш имеет смысл частоты соответствующей гармонической составляющей f (х). Важно отметить, что функция, выражающая преобразование Фурье, комплексна, даже если f(x) является действительной.
Глава 4.4.1. Об интегральных преобразованиях функций
Вообще говоря, интегральные преобразования по определению ставят в соответствие некоторой функции
f (х) другую функцию от другого аргумента F(w). Причем это соответствие f (x)-»F(co) задается интегральной зависимостью. Символьный процессор Mathcad позволяет осуществлять три вида интегральных преобразований функций — преобразование Фурье, Лапласа и Z-преобразование. Наряду с прямыми преобразованиями имеется возможность совершать любое из этих трех обратных преобразований, т. е.
F(w)->f (x) .
Аналитически все интегральные преобразования выполняются аналогично символьному интегрированию (см. разд. 4.2.2). Для вычисления преобразования выражения выделяется переменная, по которой будет осуществляться преобразование, и затем выбирается соответствующий пункт меню. Преобразования с применением оператора символьного вывода используются с одним из соответствующих ключевых слов, вслед за которым требуется указать имя нужной переменной.
Приведем примеры символьного расчета каждого из трех интегральных преобразований, а также расскажем о численных методах Фурье- и вейвлет-преобразований.
Глава 4.4.2. Аналитическое преобразование Фурье
Аналитический расчет преобразования Фурье при помощи меню показан на рис. 4.9, для чего используется команда меню
Symbolics / Transform / Fourier (Символика / Преобразование / Фурье). В листинге 4.12 приведены два примера вычисления прямого преобразования Фурье с применением ключевого слова
fourier и оператора символьного вывода —». Листинг 4.13 иллюстрирует применение обратного преобразования Фурье и последующее прямое преобразование полученного выражения, в результате которого получается исходная функция.
ВНИМАНИЕ!
Помните о том, что результаты символьных преобразований могут включать спецфункции, которые не являются встроенными функциями Mathcad и поэтому не могут впоследствии использоваться в вычислениях. Их имена представляют собой не более, чем текстовое сообщение.
Листинг 4.12. Примеры прямого преобразования Фурье


Рис. 4.9. Расчет Фурье-преобразования при помощи меню
Листинг 4.13. Обратное и прямое преобразование Фурье

Глава 4.4.3. Дискретное преобразование Фурье
В предыдущем разделе рассказывалось о возможностях символьного процессора Mathcad, позволяющего осуществить аналитическое преобразование Фурье функции, заданной формулой. Между тем огромный пласт задач вычислительной математики связан с расчетом интегралов Фурье для функций, либо заданных таблично (например, представляющих собой результаты какого-либо эксперимента), либо функций, проинтегрировать которые аналитически не удается. В данном случае вместо символьных преобразований приходится применять численные методы интегрирования, связанные с дискретизацией подынтегральной функции и называемые потому дискретным Фурье-преобразованием.
В численном процессоре Mathcad дискретное преобразование Фурье реализовано при помощи популярнейшего алгоритма быстрого преобразования Фурье (сокращенно БПФ). Этот алгоритм реализован в нескольких встроенных функциях Mathcad, различающихся только нормировками:
fft(y) — вектор прямого преобразования Фурье; FFT (у) — вектор прямого преобразования Фурье в другой нормировке; ifft (w) — вектор обратного преобразования Фурье; IFFT (w) — вектор обратного преобразования Фурье в другой нормировке:
у — вектор действительных данных, взятых через равные промежутки значений аргумента; w — вектор действительных данных Фурье-спектра, взятых через равные промежутки значений частоты.
ВНИМАНИЕ!
Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно 2n элементов (n — целое число). Результатом является вектор с 1+2n-1 элементами. И наоборот, аргумент обратного Фурье-преобразования должен иметь
1+2n-1 элементов, а его результатом будет вектор из 2n элементов. Если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями.
В листинге 4.14 показан пример расчета Фурье-спектра для модельной функции f (x), представляющей собой сумму двух синусоид разной амплитуды (верхний график на рис. 4.10). Расчет проводится по N=128 точкам, причем предполагается, что интервал дискретизации данных уi равен h. В предпоследней строке листинга корректно определяются соответствующие значения частот
W, а в последней применяется встроенная функция FFT. Полученный график Фурье-спектра показан на рис. 4.10 (снизу). Обратите внимание, что результаты расчета представляются в виде его модуля, поскольку сам спектр, как уже отмечалось, является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра с определением синусоид в начале листинга.
ПРИМЕЧАНИЕ
Более подробную информацию о свойствах и практике применения Фурье-преобразования вы найдете в главе 14.
Листинг 4.14. Дискретное преобразование Фурье (алгоритм
БПФ) модельнго сигнала


Рис. 4.10. Модельная функция и ее преобразование Фурье (продолжение листинга 4.14)
Глава 4.4.4. Преобразование Фурье комплексных данных
Алгоритм быстрого преобразования Фурье для комплексных данных встроен в соответствующие функции, в название которых входит литера "с":
cfft(y) — вектор прямого комплексного преобразования Фурье; CFFT(y) — вектор прямого комплексного преобразования Фурье в другой нормировке; icfft(y) — вектор обратного комплексного преобразования Фурье; ICFFT(w) — вектор обратного комплексного преобразования Фурье в другой нормировке:
у — вектор данных, взятых через равные промежутки значений аргумента; w — вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.
Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля, и выводят только его половину (см. разд. 4.4.3). Поэтому, в частности, по 128 действительным данным получалось всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье (рис. 4.11), то получится вектор из 128 элементов. Сравнивая рис. 4.10 и 4.И, можно уяснить соответствие между результатами действительного и комплексного Фурье-преобразования.

Рис. 4.11. Комплексное преобразование Фурье (продолжение листинга 4.14)
Глава 4.4.5. Двумерное преобразование Фурье
В Mathcad имеется возможность вычислять не только одномерное преобразование Фурье функции f (x), но и двумерное преобразование функции двух переменных f(x,y). Иными словами, допускается применять встроенные
функции комплексного дискретного преобразования Фурье не только к одномерным, но и к двумерным массивам, т. е. матрицам. Соответствующий пример приведен в листинге 4.15 и на рис. 4.12 в виде графика поверхности исходных данных (верхний график) и рассчитанного двумерного Фурье-спектра (нижний график).

Рис. 4.12. Функция двух переменных и ее двумерное преобразование Фурье (продолжение листинга 4.15)
Листинг 4.15. Двумерное дискретное преобразование Фурье

Глава 4.5. Другие интегральные преобразования
Рассмотрим в завершение главы, посвященной интегрированию, еще три преобразования, которые часто применяются помимо интеграла Фурье. Отметим, что преобразование Лапласа и Z-преобразование встречаются в практических задачах вычислительной математики относительно редко, а вот вейвлет-преобразование, теория которого появилась относительно недавно, постепенно выходит на лидирующие позиции в проблемах обработки данных.
Глава 4.5.1. Преобразование Лапласа
Преобразованием Лапласа называют интеграл от f (х) следующего вида:

Рассчитывается преобразование Лапласа совершенно аналогично Фурье-преобразованию (см. разд. 4.4). Примеры преобразования Лапласа приведены в листинге 4.16 и на рис. 4.13.
Листинг 4.16. Двумерное преобразование Лапласа

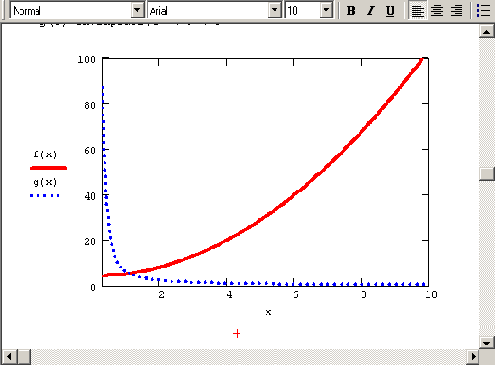
Рис. 4.13. Прямое и обратное преобразование Лапласа (продолжение листинга 4.16)
Глава 4.5.2. Z-преобразование
Z-преобразование функции f (х) определяется не интегралом, а бесконечной суммой следующего вида:
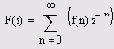
Пример Z-преобразования приведен в листинге 4.17, а его результаты — на рис. 4.14.
Листинг 4.17. Прямое и обратное Z-преобразование


Рис. 4.14. Прямое и обратное Z-преобразования (продолжение листинга 4.17)
Глава 4.5.3. Вейвлет-преобразование
В последнее время возрос интерес к другим интегральным преобразованиям, в частности, к вейвлет-преобразованию (или дискретному волновому преобразованию). Оно применяется, главным образом, для анализа нестационарных сигналов и для многих задач подобного рода оказывается более эффективным, чем преобразование Фурье. Основным отличием вейвлет-преобразования является разложение данных не по синусоидам (как для преобразования Фурье), а по другим функциям, называемым вейвлетобразующими. Вейвлетобразующие функции, в противоположность бесконечно осциллирующим синусоидам, локализованы в некоторой ограниченной области своего аргумента, а вдали от нее равны нулю или ничтожно малы. Пример такой функции, называемой "мексиканской шляпой", показан на рис. 4.15.
По своему математическому смыслу вейвлет-спектр имеет не один аргумент, а два. Помимо частоты, вторым аргументом ь является место локализации вейвлетобразующей функции. Поэтому ь имеет ту же размерность, что и х.
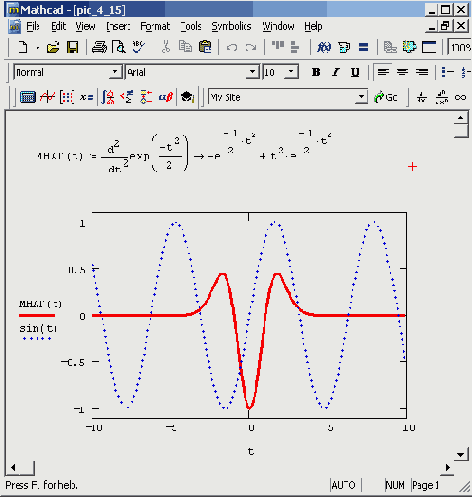
Рис. 4.15. Сравнение синусоиды и вейвлетобразующей функции
Встроенная функция вейвлет-преобразования
Mathcad имеет одну встроенную функцию для расчета вейвлет-преобразования на основе вейвлетобразующей функции Добеши:
wave (у) — вектор прямого вейвлет-преобразования Добеши; iwave (v) — вектор обратного вейвлет-преобразования Добеши:
Аргумент функции вейвлет-преобразования, т. е. вектор у, должен так же, как и в преобразовании Фурье, иметь ровно 2П элементов (n — целое число). Результатом функции wave является вектор, скомпонованный из нескольких коэффициентов с двухпараметрического вейвлет-спектра. Особенности использования функции wave иллюстрируются листингом 4.18, где в качестве модельной функции взята сумма двух синусоид, график которой был изображен на рис. 4.10. Результаты вычислений вейвлет-спектра Добеши представлены в виде трех семейств его коэффициентов на рис. 4.16.
Листинг 4.18. Вычисление вейвлет-спектра
Добеши модельного сигнала


Рис. 4.16. Вейвлет-спектр Добеши модельного сигнала (продолжение листинга 4.18)
Программирование других вейвлет-преобразований
Наряду со встроенной функцией wave, профессиональные версии Mathcad 11—12 снабжены пакетом расширения для осуществления вейвлет-анализа. Пакет расширения содержит большое число дополнительных встроенных функций, имеющих отношение к вейвлет-преобразованиям. Обзор пакетов расширения выходит за рамки данной книги, поэтому ограничимся простым упоминанием об этой возможности.
ПРИМЕЧАНИЕ
Дополнительную информацию об использовании данных встроенных функций можно найти в соответствующей .электронной книге, которую можно открыть при помощи меню Help/ E-Books / Wavelet extension pack (Справка/ Электронные книги / Вейвлет-анализ данных).
Помимо встроенной функции вейвлет-спектра Добеши и возможностей пакета расширения, допускается непосредственное программирование алгоритмов пользователя для расчета вейвлет-спектров. Оно сводится к аккуратному численному расчету соответствующих семейств интегралов. Один из примеров такой программы приведен в листинге 4.19. Анализу подвергается функция, составленная из суммы двух синусов, а график двухпараметриче-ского спектра с(а,b) выведен на рис. 4.17 в виде привычных для вейвлет-анализа линий уровня на плоскости (а,b).
ПРИМЕЧАНИЕ
Программа листинга очень проста, но исключительно далека от хорошей в смысле быстродействия. Каждый интеграл вычисляется независимо, без использования методов ускорения, типа применяемых в алгоритме БПФ. Однако простые приемы программирования вполне доступно раскрывают математический смысл вейвлет-преобразования.
Листинг 4.19. Вычисление вейвлет-спектра на основе "мексиканской шляпы"


Рис. 4.17. Вейвлет-спектр модельного сигнала на основе "мексиканской шляпы" (продолжение листинга 4.19)