Математические задачи в пакете MathCAD 12
Глава 6.1. Поиск экстремума функции
Для численного решения задач поиска локального максимума и минимума в Mathcad имеются встроенные функции
Minerr, Minimize и Maximize. Принцип их действия очень близок к принципу расчетов, заложенных во встроенной функции
Find, предназначенной для решения алгебраических уравнений (см. главу 5). В частности, все встроенные функции минимизации используют те же градиентные численные методы, что и функция
Find, поэтому допускается "вручную" выбирать численный алгоритм минимизации из уже рассмотренных нами численных методов (см. разд. 5.3.2). Кроме того, как и в случае решения уравнений, применение градиентного алгоритма, во-первых, требует задания некоторого начального приближения к точке минимума и, во-вторых, позволяет отыскать лишь один (т. е. локальный) из минимумов функции.
Таким образом, как и в случае решения уравнений (см. разд. 5.2.4), чтобы найти глобальный максимум (или минимум), требуется сначала просканировать с некоторым шагом рассматриваемую область и вычислить все локальные значения и потом выбрать из них наибольший (наименьший). Другим вариантом будет простое сканирование с вычислением значений функции, позволяющее выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в
зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.
Глава 6.1.1. Локальный экстремум
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно:
Minimize (f,x1, ... ,хM) — вектор значений аргументов, при которых функция f достигает минимума; Maximize (f,x1, ... ,хM) — вектор значений аргументов, при которых функция f достигает максимума:
f (x1,..., хM,...)—функция; x1,...,хM — аргументы, по которым производится минимизация (максимизация).
ПРИМЕЧАНИЕ
Вычислительный блок (ключевое слово Given со следующими после него логическими выражениями) обычно используется в задачах на условный экстремум (см. следующий разд.).
В качестве примера рассмотрим задачу численного поиска экстремумов полинома четвертой степени f (х), график которого был приведен на рис. 6.1. Как известно, парабола четвертой степени имеет три точки экстремума, и все они видны на рис. 6.1.
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления локальных экстремумов функции одной переменной показаны в листингах 6.1—6.2. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений х от
-oo до oo.
Листинг 6.1. Поиск минимума функции одной переменной
(для трех начальных значений x)

Листинг 6.2. Поиск максимума функции одной переменной

Как видно из листингов, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы. Очень полезно сопоставить результаты минимизации (листинг 6.1) с графиком функции f(x) (см. рис. 6.1). Как видно, функция
Minimize очень уверенно находит глубокий минимум х=-0.75. А вот на второй (плохо выраженный) минимум можно набрести лишь случайно, выбирая определенные начальные значения х. В последнем из трех примеров демонстрируется, что если взять начальное приближение
х даже в непосредственной близости от этого локального минимума, численный метод все равно "сваливается" в первый, более глубокий минимум
f(х). Попробуйте повторить расчеты, выбирая различные начальные значения, чтобы в этом убедиться.
В листинге 6.2 показаны аналогичные свойства функции Maximize. Если начальное приближение выбрать удачно, то итерационный процесс алгоритма сойдется к максимуму функции, а вот если выбрать его вдали от него, на участке
f (х), где неограниченно возрастает (при х->±oo), численный метод вообще не справится с задачей, выдавая сообщение об ошибке. Это происходит, поскольку начальное приближение
х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения
f (х), т. е. расходится при х->oo.
ПРИМЕЧАНИЕ
Помните о возможности выбора численного алгоритма минимизации, который осуществляется при помощи контекстного меню (рис. 6.2). Не забывайте также, что, начиная с версии Mathcad 11, имеется возможность управлять параметром Multistart (Сканирование), при помощи которого можно попытаться организовать поиск глобального экстремума (см. разд. 5.3.2). Однако не слишком полагайтесь на эту опцию и, если перед вами стоит задача поиска глобального экстремума, постарайтесь организовать сканирование вручную.

Рис. 6.2. Выбор численного метода минимизации
Глава 6.1.2. Условный экстремум
В задачах на условный экстремум встроенные функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово
Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. Листинги 6.3 и 6.4 содержат примеры поиска условного экстремума на различных интервалах, определенных неравенствами. У вас не должны возникнуть сложности с записью условий в Mathcad, а вот разобраться в скрытой от глаз вычислительной стороне будет полезно. С этой точки зрения поучительно сравнить результаты работы приведенных листингов с листингами 6.1 и 6.2 соответственно.
Листинг 6.3. Поиск условного минимума
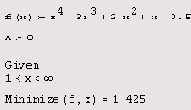
Листинг 6.4. Поиск условного максимума
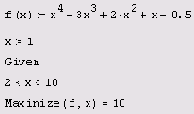
Как видно из листинга 6.3, если ограничить значения х интервалом, расположенным в окрестности правого локального максимума, с поиском которого мы встретили большие сложности при решении задачи на безусловный экстремум, то этот максимум будет без труда найден численным методом. Следует помнить также об одной особенности, иллюстрируемой листингом 6.4. А именно (в случае максимизации), если на границе интервала
f (x) достигает большего значения, нежели на локальном максимуме внутри интервала, то в качестве решения, скорее всего, будет выдано наибольшее значение (т. е. граница интервала).
Конечно, если на рассматриваемом интервале х расположено несколько локальных максимумов, ответ станет еще менее предсказуемым, поскольку будет напрямую зависеть от выбранного начального приближения. Не забывайте о важности его правильного выбора и в случае задач на условный экстремум. В частности, если вместо начального значения х=-1 задать
х=1, то в качестве максимума будет найдена правая граница интервала: Maximize (f,x) =2, что неверно, поскольку максимальное значение достигается функцией
f (х) на левой границе интервала при х=-3. Выбор начального приближения
х=-4 решает задачу правильно, выдавая в качестве результата Maximize(f,x)=-5.
Глава 6.1.3. Экстремум функции нескольких переменных
Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Поэтому ограничимся примером нахождения максимума и минимума функции, показанной в виде графиков трехмерной поверхности и линий уровня (листинг 6.5). Привлечем внимание читателя только к тому, как с помощью неравенств, введенных логическими операторами, задается область на плоскости
(X,Y).

Рис. 6.3. Иллюстрация задачи на условный экстремум функции
двух переменных: график функции f (х, у) и отрезок прямой х+у=10
(продолжение листинга 6.5)
Листинг 6.5. Экстремум функции двух переменных

Дополнительные условия могут быть заданы и равенствами. Например, определение после ключевого слова
Given уравнения х+у=10 приводит к такому решению задачи на условный экстремум:

Как нетрудно сообразить, новое дополнительное условие означает, что численный метод ищет минимальное значение функции
f(x,y) не во всей прямоугольной области (х, Y) , а лишь вдоль отрезка прямой, показанного на рис. 6.3.
ПРИМЕЧАНИЕ
Поиск минимума можно организовать и с помощью функции Minerr. Для этого в листинге 6.5 надо поменять имя функции
Minimize на Minerr, а после ключевого слова Given добавить выражение, приравнивающее функции f (x,y)
значение, заведомо меньшее минимального, например, f (х, у) =0.
Глава 6.1.4. Пример: линейное программирование
Задачи поиска условного экстремума функции многих переменных часто встречаются в экономических расчетах для минимизации издержек, финансовых рисков, максимизации прибыли и т. п. Целый класс экономических задач оптимизации описывается системами линейных уравнений и неравенств. Они называются задачами линейного программирования. Приведем характерный пример так называемой транспортной задачи, которая решает одну из проблем оптимальной организации доставки товара потребителям с точки зрения экономии транспортных средств (листинг 6.6).
Листинг 6.6. Решение задачи линейного программирования

Модель типичной транспортной задачи следующая. Пусть имеется N предприятий-производителей, выпустивших продукцию в количестве
b0, ... ,bN-1 тонн. Эту продукцию требуется доставить м потребителям в количестве
а0, ... „аM-1 тонн каждому. Численное определение векторов а и
b находится в первой строке листинга. Сумма всех заказов потребителей
ai равна сумме произведенной продукции, т. е. всех
bi (проверка равенства во второй строке). Если известна стоимость перевозки тонны продукции от
i-го производителя к j-му потребителю
Ci,j, то решение задачи задает оптимальное распределение соответствующего товаропотока
xi,j с точки зрения минимизации суммы транспортных расходов. Матрица с и минимизируемая функция f (х) матричного аргумента х находятся в середине листинга 6.6.
Условия, выражающие неотрицательность товаропотока, и равенства, задающие сумму произведенной каждым предприятием продукции и сумму заказов каждого потребителя, находятся после ключевого слова Given. Решение, присвоенное матричной переменной
sol, выведено в последней строке листинга вместе с соответствующей суммой затрат. В строке, предшествующей ключевому слову
Given, определяются нулевые начальные значения для х простым созданием нулевого элемента матрицы
xN-1,M-1.
ПРИМЕЧАНИЕ 1
Если взять другие начальные значения для х, решение, скорее всего, будет другим! Возможно, вы сумеете отыскать другой локальный минимум, который еще больше минимизирует транспортные затраты. Это еще раз доказывает, что задачи на глобальный минимум, к классу которых относится линейное программирование, требуют аккуратного отношения в смысле выбора начальных значений. Часто ничего другого не остается, кроме сканирования всей области начальных значений, чтобы из множества локальных минимумов выбрать наиболее глубокий.
ПРИМЕЧАНИЕ 2
Не забывайте о том, что в вычислительном блоке в качестве неизвестных следует использовать все компоненты вектора х, как это сделано в предпоследней строке листинга 6.6 (с/и. разд. 5.1.1). Иными словами, нельзя задавать некоторые из компонент х в виде параметров.
ПРИМЕЧАНИЕ 3
Еще раз напомним, что в новых версиях Mathcad (начиная с 11-й) появилась возможность программного управления глобальной минимизацией. Для этого служит параметр численного алгоритма
Multistart (Сканирование), который следует установить в положение Yes (Да) для поиска глобального экстремума (см. разд. 5.3.2). Любопытно, что если при решении нашей задачи поменять только эту опцию функции
Minimize, то численный метод даст сбой, и вместо решения появится сообщение об ошибке. Однако если вспомнить, что наша транспортная задача — линейная, и выставить в контекстном меню, вызываемом на имени функции
Minimize, флажок Linear (Линейный), задающий линейный вариант алгоритма, то глобальное решение будет найдено.
Глава 6.1.5. Аналитическое решение задач на экстремум
Несмотря на то, что, как уже говорилось, разработчиками Mathcad символьное решение задач оптимизации не предусмотрено, пользователь все-таки имеет возможность аналитического исследования экстремумов функций, опираясь на базовые сведения математического анализа. Следует лишь вспомнить о том, что (при выполнении соответствующих условий на непрерывность и гладкость функции) точки экстремума
f(x) характеризуются тем, что в них производная этой функции проходит через нулевое значение. Тип экстремума (максимум или минимум) определяется знаком второй производной в этой точке.
Таким образом, имея в виду данные правила, не представляет особого труда организовать аналитическое решение задачи на экстремум, центральным моментом которого будет решение алгебраического уравнения
f (x)=0. Сразу стоит подчеркнуть, что можно использовать гибрид символьных и аналитических расчетов, когда, например, производная f (x) считается аналитически, а уравнение
f (x)=0 (если символьное решение получить не удается) — численно. В этом случае во всей красе может проявиться мощь
Mathcad, предоставляющего пользователю богатый арсенал как аналитических, так и численных методов.
Приведем несложный пример реализации аналитического поиска экстремумов той же функции (полинома 4-й степени), которая использовалась нами при демонстрации возможностей численных методов (см. разд. 6.1.1). В листинге 6.7, в первой строке, приводится определение
f(x), а затем при помощи символьного процессора осуществляется отыскание корней нелинейного уравнения
f (x)=0. Результатом решения являются все три точки экстремума (последняя строка листинга). На рис. 6.4 показан график функций
f (х) и f (x), и легко убедиться, что экстремумам исходной функции соответствуют нули ее производной.
Листинг 6.7. Аналитический поиск экстремумов функции
одной переменной

Чтобы завершить анализ f (х) на экстремумы, необходимо определить, какие из найденных точек являются точками минимума, а какие — максимума. Для этого (листинг 6.8) следует просто рассчитать значения второй производной в результатах решения уравнения и определить ее знак.
Листинг 6.8. Анализ типа точек экстремума (продолжение
листинга 6.7)
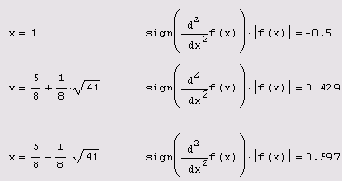

Рис. 6.4. Функция f (x) и ее производная (продолжение листинга 6.7)
Глава 6.2. Приближенное решение алгебраических уравнений
Градиентные численные методы решения задач отделения корней уравнений и поиска экстремума функций очень близки. Поэтому, в частности, пользователь может тем же самым образом, с помощью контекстного меню, выбирать конкретный метод приближенного решения для функций
Minimize и Maximize. Применительно к нелинейным уравнениям основная идея градиентных алгоритмов была приведена в разд. 5.3.2. Основным отличием в случае задач минимизации является критерий правильности решения (прекращения итераций): если при решении уравнений критерием служит близость нулю невязки системы уравнений, то при минимизации критерий заключается в схождении итераций к минимальным значениям исследуемой функции.
Близость рассмотренных задач связана также с тем, что иногда приходится заменять проблему решения нелинейных уравнений задачей поиска экстремума функции многих переменных. Например, когда невозможно найти решение с помощью функции
Find, можно попытаться потребовать вместо точного выполнения уравнений условий минимизировать их невязку. Чтобы не нужно было реализовывать данную схему вручную (вместо встроенной функции
Find использовать соответствующую постановку задачи для функции Minimize), разработчики Mathcad предусмотрели дополнительную встроенную функцию
Minerr. Она применяется аналогично функции Find (см. разд. 5.1. Т), в частности, имеет тот же самый набор параметров и должна находиться в пределах вычислительного блока:
1. x1:=C1 ... хM:=CM — начальные значения для неизвестных.
2. Given — ключевое слово.
3. Система алгебраических уравнений и неравенств, записанная логическими операторами.
4. Minerr (x1, ... ,хM) — приближенное решение системы относительно переменных
x1, ... ,хM, минимизирующее невязку системы уравнений.
ПРИМЕЧАНИЕ 1
В функции Minerr реализованы те же самые алгоритмы, что и в функции Find, иным является только условие завершения работы численного метода (как в случае функций
Minimize и Maximize).
ПРИМЕЧАНИЕ 2
Согласно своему математическому смыслу, функция Minerr может применяться для построения регрессии серии данных по закону, заданному пользователем (см. главу 13).
Пример использования функции Minerr показан в листинге 6.9. Как видно, достаточно заменить в вычислительном блоке имя функции на
Minerr, чтобы вместо точного (конечно, с поправкой на погрешность порядка
TOL) получить приближенное решение уравнения, заданного после ключевого слова
Given.
Листинг 6.9. Приближенное численное решение уравнения,
имеющего корень (x=0, y=0)

Листинг 6.9 демонстрирует приближенное решение уравнения kx2+y2=0, которое при любом значении коэффициента
k имеет единственный точный корень (х=0,у=0). Тем не менее при попытке решить его функцией
Find для больших k, порядка принятых в листинге (рис. 6.5), происходит генерация ошибки
"No solution was found" (Решение не найдено). Это связано с иным поведением функции f (x,y)=kx2+y2
вблизи ее корня по сравнению с функциями, поиск корней которых был разобран в предыдущей главе (см. рис. 5.1).
В отличие от них, f (х,у) не пересекает плоскость f (х,у)=0, а лишь касается ее (рис. 6.5) в точке
(х=0,у=0). Поэтому и найти корень изложенными в предыдущем разделе градиентными методами намного сложнее, поскольку вблизи корня производные f (х,у) близки к нулю, и итерации, строящиеся по градиентному принципу, могут уводить предполагаемое решение далеко от корня.
Ситуация еще более ухудшается, если наряду с корнем типа касания (как на рис. 6.5) имеются (возможно, весьма удаленные) корни типа пересечения. Тогда попытка решить уравнение или систему уравнений с помощью функции
Find может приводить к нахождению корня второго типа, даже если начальное приближение было взято очень близко к первому. Поэтому если вы предполагаете, что система уравнений имеет корень типа касания, намного предпочтительнее использовать функцию
Minerr, тем более что всегда есть возможность проконтролировать невязку уравнений простой подстановкой полученного решения в исходную систему уравнений. Пока мы рассматривали пример нахождения существующего решения уравнения. Приведем теперь пример нахождения функцией
Minerr приближенного решения не имеющего корней уравнения (листинг 6.10), а также несовместной системы уравнений и неравенств (листинг 6.11). Решение, выдаваемое функцией
Minerr, минимизирует невязку данной системы. Как видно из листингов, в качестве результата выдаются значения переменных, наилучшим образом удовлетворяющие уравнению и неравенствам внутри вычислительного блока.
ВНИМАНИЕ!
Полученное в листинге 6.11 решение не удовлетворяет неравенствам, составляющим задачу. Это и неудивительно, поскольку точного решения системы нет, и в качестве ответа Mathcad выдает значения аргументов, минимизирующих норму общей невязки (не отдавая предпочтения ни уравнению, ни неравенствам).

Рис. 6.5. Поиск минимума и попытка нахождения корня
функции f (x, у) =kx2+y2
Листинг 6.10. Приближенное решение уравнения x2+y2+1=0

Листинг 6.11. Приближенное решение несовместной системы уравнений и
неравенств
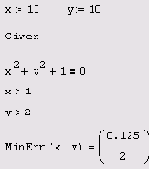
Внимательный читатель может обнаружить, что решение, выдаваемое функцией Minerr в рассматриваемом примере, не является единственным, поскольку множество пар значений (х,у) в равной степени минимизирует невязку данной системы уравнений и неравенств. Поэтому для различных начальных значений будут получаться разные решения, подобно тому, как разные решения выдаются функцией
Find в случае бесконечного множества корней (см. разд. 5.2.4). Еще более опасен случай, когда имеются всего несколько локальных минимумов функции невязки. Тогда неудачно выбранное начальное приближение приведет к выдаче именно этого локального минимума, несмотря на то, что другой (глобальный) минимум невязки может удовлетворять системе гораздо лучше.
В завершение раздела сделаем очень важное замечание, связанное с возможностью использования встроенной функции
Minerr в символьных расчетах. Как и функция решения алгебраических систем
Find, она может применяться без предварительного присвоения каких-либо начальных значений любым переменным, входящим в уравнение, как это проиллюстрировано листингом 6.12, решающим ту же самую задачу аналитически. Замечательно, что в результате получается не одно решение, а все семейство решений, одинаково минимизирующее невязку.
Листинг 6.12. Аналитическое приближенное решение уравнения
kx2+y2+1=0

Глава 6.3. Пример: регуляризация некорректных задач
Еще один широко распространенный круг задач на решение систем уравнений, называемых обратными, наиболее типичен для современной экспериментальной физики. Значительную часть обратных задач относят к классу некорректно поставленных (или просто некорректных), которые, благодаря своей принципиальной неустойчивости, требуют специального подхода. Как правило, общим принципом решения некорректных задач является их регуляризация, заключающаяся в их сведении к задаче минимизации.
Глава 6.3.1. О постановке некорректных задач
Рассмотрим сначала типичную постановку обратных задач, а затем обратимся к обсуждению корректности их постановки.
Обратные задачи
Строго говоря, обратные задачи связаны, как правило, не с отысканием значения корня уравнения (или системы) f (x)=o, а с вычислением неизвестной функции у (х), описываемой уравнением
S[y(x)]=b(x). (6.1)
Здесь A[у] — некоторый функционал (т. е. функция от функции), а
b(х) — известная функция (правая часть уравнения).
Рассмотрим типичную постановку обратных задач на примере так называемой инструментальной задачи. Пусть имеется некоторый сигнал у(х), который подвергается измерению на приборе, условно обозначаемом
S. Физику-исследователю доступно измерение данного сигнала, которое находится на
выходе прибора (дисплее, табло и т.п.). Обозначим это измерение
b(х). Поскольку прибор вносит в сигнал, во-первых, искажения (например, в устройствах типа спектрометров часто измеряются некоторые интегральные характеристики сигнала) и, во-вторых, шумовую компоненту. Формально данную физическую модель можно записать равенством (6.1), в котором оператором s обозначается аппаратная функция, т. е. действие прибора на сигнал
у (х).
Листинг 6.13. Пример моделирования прямой задачи, выражающей линейную
схему измерений


Рис. 6.6. Исходный сигнал и показания прибора (продолжение листинга 6.13)
Согласно изложенной модели, измерения b(х) могут довольно сильно отличаться от исходного сигнала у(х), что иллюстрируется простым примером
листинга 6.13 и рис. 6.6. В первой строке листинга выбирается модельный сигнал у(х), а во второй и третьей — определяется оператор
S[y(x)]. Важно отметить, что использованная структура оператора — интегральная зависимость от сигнала
у (х) в сумме с шумовой компонентой — наиболее типична для инструментальных обратных задач. Читателю будет очень полезно "поиграть" с параметрами задачи
k и сигма (эффективной шириной спектральной характеристики прибора и интенсивностью шума соответственно), чтобы "почувствовать" специфику модели измерений. Несколько примеров расчетов
b(х), согласно листингу 6.13, приведено на рис. 6.7 в виде коллажа нескольких графиков.

Рис. 6.7. Расчеты показаний прибора (коллаж результатов листинга 6.17 для различных сочетаний параметров k и 0)
ПРИМЕЧАНИЕ 1
Модель измерений, представленная в третьей строке листинга 6.13, описывает, с математической точки зрения, типичное интегральное уравнение, в которое неизвестная функция у(х) входит в виде части подынтегральной функции. Класс обратных задач чаще всего (но не всегда) соответствует как раз интегральным уравнениям.
ПРИМЕЧАНИЕ 2
Неизвестная функция у (х) входит в модель, приведенную в листинге 6.13, линейным
образом (в первой степени под знаком интеграла). В связи с этим рассматриваемая задача является линейной, а саму модель называют часто линейной схемой измерений. Линейность модели проявляется также в том, что ее дискретная форма записывается в виде матричного соотношения (см. листинг 6.14 ниже).
Из сказанного выше понятно, что в практических приложениях весьма актуальна задача восстановления сигнала у(х)
по показаниям прибора b(х) (при наличии определенной дополнительной информации о физике измерения, т. е. об операторе
S, выражающем действие прибора). Таким образом, в отличие от прямой задачи, выражающейся равенством (6.1), обратной задачей является восстановление функции
у (х) по известной b(х).
Обычно сигнал (и, соответственно, его измерение) может зависеть от времени и/или пространственных координат. Эту зависимость мы обозначили как зависимость от х. При использовании численных методов непрерывные зависимости от х дискретизируются, заменяясь соответствующими векторами. Таким образом, задача отыскания неизвестной функции
у(х) заменяется задачей поиска неизвестного вектора Y и может быть записана в матричном виде
S(Y)=B, (6.2)
где вектор у неизвестен, а оператор S (в линейном случае S(Y)=AY, где
А — матрица) и вектор правых частей уравнений в известны. Таким образом, в дискретном случае обратная задача для рассматриваемой математической модели состоит в решении системы (в общем случае, нелинейных) уравнений (6.2). Построенная описанным способом дискретная задача представлена в листинге 6.14. Важно отметить, что, поскольку исходная задача линейна, дискретный вариант ее оператора записывается в виде матрицы
А, а сама задача сводится к системе линейных алгебраических уравнений AY=B.
ПРИМЕЧАНИЕ
Рекомендуем читателю обратиться к соответствующему файлу Mathcad на прилагаемом к книге компакт-диске и сравнить графики сигнала и измерений, соответствующие непрерывной (интегральной) и дискретной (матричной) модели. Будет очень полезным осуществить расчеты для разных значений параметров, в том числе количества точек дискретизации м, а также разобраться, какова структура матрицы
А.
Листинг 6.14. Дискретная форма прямой задачи линейной
модели измерений (продолжение листинга 6.13)

Некорректные задачи
При решении обратных задач важную роль играет их устойчивость. Задача устойчива, если малым флуктуациям правых частей, т. е. вектора в, соответствуют малые флуктуации решения Y. Иными словами, устойчивость по правой части состоит в требовании, чтобы решения близких задач
AY=B и AY=B+σB мало отличались друг от друга. Если задача изначально является неустойчивой, то решать ее нет смысла, поскольку погрешности алгоритмов, накапливающиеся в ходе решения численными методами, неизбежно приведут к тому, что будет найдено неверное решение.
Как правило (в том числе в нашем примере), обратные задачи характеризуются наличием шумов, что может быть символически отражено равенством (если опять-таки предположить, что шум ст входит в схему измерений линейно):
AY+σ=B. (6.3)
Наличие шума коренным образом меняет идеологию решения обратных задач. Если сама задача является устойчивой, то существование шума может эту устойчивость нарушать. Попросту говоря, различные (даже очень сильно отличающиеся) сигналы
Y1 и Y2 могут, будучи искажены шумом, приводить к очень похожим измерениям
В1~B2. Поэтому встает вопрос, можно ли извлечь из измерений полезную информацию о сигнале, если наличие шума делает задачу неустойчивой? Такие задачи называются задачами, поставленными некорректно, и для их решения развиты специальные методы, основанные на привлечении дополнительной априорной информации о решении Y, которые будут рассмотрены ниже. Следует также отметить, что класс некорректных задач шире класса обратных (один из примеров вы найдете в конце разд. 11.1.2).
Сказанное иллюстрирует рис. 6.8, на котором представлена попытка решения задачи листингов 6.13 и 6.14 "в лоб", прямым обращением матрицы А. Реконструкция сигнала путем простого обращения матрицы А оказывается возможной лишь для очень низких значений уровня шума а, а при увеличении шума решение
Y=A-1B оказывается совершенно нефизическим. Очевидно, что для получения осмысленного результата следует применять иные методы.

Рис. 6.8. Исходный сигнал и попытка его реконструкции А-1В (продолжение листингов 6.13 и 6.14) для
σ=10-5
ПРИМЕЧАНИЕ
Проблемы, возникающие при попытке обращения матрицы А, связаны с ее плохой обусловленностью. Подход к подобным задачам может быть не обязательно таким, как рассказывается в двух следующих разделах (см. главу 8).
Глава 6.3.2. Квазирешение
Одним из наиболее простых методов решения некорректных обратных задач является концепция поиска их квазирешения. Рассмотрим обратную задачу
AY=B, где неизвестный вектор Y подлежит определению, а оператор (в линейном случае, матрица)
А и вектор правых частей уравнений в известны. Подчеркнем, что задача может быть и нелинейной, т. е. оператор
А может описывать сложную зависимость.
Основная идея квазирешения состоит в параметризации неизвестного вектора Y, исходя из физических соображений постановки задачи. То есть на основе некоторой имеющейся априорной информации следует заранее задать модельный вид
Y~Y0, зависящий от ряда параметров r1,r2,... В результате пространство поиска решений значительно сужается — вместо отыскания всех компонент вектора
Y требуется лишь найти значения модельных параметров, решающих (в определенном смысле) задачу.
Квазирешение Y0 находится из решения задачи на минимум:
r=arg min{ IA-YO (r)-B| }, (6.4)
где минимизация проводится по вектору S параметров модельной зависимости
Y0 (r). Следует подчеркнуть, что задача поиска квазирешения является задачей на глобальный экстремум, что важно с позиций выбора вычислительного метода (как уже отмечалось, наиболее популярны градиентные методы поиска минимума в комбинации со сканированием для достижения глобальной минимизации — алгоритмами сплошного или случайного поиска).
Пример отыскания квазирешения обсуждавшейся в предыдущих разделах задачи приведен в листинге 6.15 и на рис. 6.9 (данные о результатах модельных измерений в и матрице А взяты из предыдущего листинга). Понятно, что при сведении некорректной задачи к проблеме отыскания квазирешения решающее значение принадлежит правильно выбранной параметризации неизвестного вектора у.

Рис. 6.9. Исходный сигнал У, измерения В и квазирешение Y0 (продолжение листинга 6.15)
Листинг 6.15. Квазирешение некорректной задачи (продолжение
листингов 6.13 и 6.14)

Глава 6.3.3. Регуляризация Тихонова
Говоря о некорректных задачах, нельзя не отметить, что для их решения советским математиком Тихоновым был предложен чрезвычайно эффективный метод, называемый регуляризацией и основанный на привлечении дополнительной априорной информации о решении, которая может быть как качественной, так и количественной. Например, можно искать решение, максимально близкое к некоторому профилю, т. е. к некоторому вектору
Y0. Концепция регуляризации сводится к замене исходной некорректной задачи на задачу о минимизации следующей функции:
Ω(Y,λ) = |АY-B|+λ|Y-Y0|, (6.5)
где λ — малый положительный параметр регуляризации, который необходимо подобрать определенным способом. Отметим, что, если рассматривать не дискретную, а непрерывную задачу (т. е. профиль
у(х) вместо вектора Y), то Ω(у(х),λ) будет представлять собой не функцию, а функционал, исторически называемый функционалом Тихонова.
Минимизируя функцию Ω(Y,λ), можно получить регуляризованное решение
Y (А), зависящее от параметра λ. Из (6.5) хорошо ясен его смысл: при малых
λ ~ 0 проблема поиска функционала близка к (некорректной) исходной задаче, а при больших
А, задача поставлена корректно, но ее решение далеко от решения исходной обратной задачи. А именно, чем больше параметр регуляризации, тем ближе решение к априорной оценке
Y0. Очевидно, что на практике необходимо выбирать промежуточные
λ.. Можно показать, что в линейном случае задача о минимизации функционала
Ω(Y,λ) может быть сведена к следующей системе линейных алгебраических уравнений (решению линейных систем посвящена глава 8):
(ATA+λI)Y=ATB+λY0. (6.6)
ПРИМЕЧАНИЕ
В общем (нелинейном) случае минимизация Ω(Y,λ) должна производиться по всем компонентам вектора
Y, что представляет собой довольно громоздкую вычислительную задачу. Как уже отмечалось, поиск глобального экстремума
осложняется не только благодаря многомерности задачи, но и из-за возможности существования нескольких локальных минимумов.

Рис. 6.10. Исходный сигнал Y, его априорная оценка 0 и измерения В (продолжение листинга 6.16)
Приведем в качестве примера применения регуляризации (листинг 6.16) решение некорректной линейной задачи интерпретации измерений, которая решалась нами ранее другими способами в листингах 6.13—6.15. В качестве модельного сигнала будем использовать квадратичную параболу, а в качестве априорной оценки — линейный профиль
Y0 (рис. 6.10). Сделаем мы это для того, чтобы соблюсти честность, пытаясь подогнать регуляризованное решение не к исходной (вообще говоря, неизвестной) модели, а к иной зависимости. В результате решения (в последней строке листинга) системы линейных уравнений (6.6), зависящей от А. как от параметра, получается зависимость регуляризованного решения (вектора
Y) от X. Соответствующая невязка системы уравнений
δ(λ) = |AY(λ)-B|, также являющаяся функцией
X, показана на рис. 6.11.
Листинг 6.16. Регуляризация некорректной линейной задачи
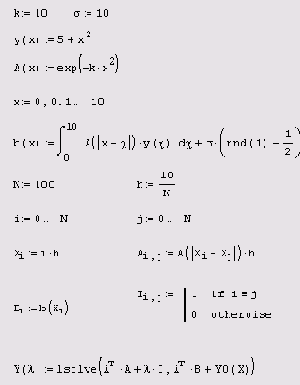

Рис. 6.11. Невязка δ(λ), даваемая регуляризованным решением Y(λ) задачи (6.6)
(продолжение листинга 6.16)
Для реконструкции можно использовать такое значение λ, которое соответствует глобальному минимуму зависимости
δ(λ). Иными словами, необходимо решить еще одну задачу на минимум, но уже другой функции
δ(λ) (листинг 6.17). Подчеркнем, что само определение этой функции подразумевает вложенную минимизацию функционала Тихонова (6.5), которую мы, правда, оформили посредством решения системы линейных уравнений (6.6). Таким образом, для построения реконструкции сигнала (она показана на рис. 6.12) нам пришлось решить две задачи минимизации.
ПРИМЕЧАНИЕ
Часто применяют и другой способ определения А, называемый принципом невязки. Он подразумевает выбор параметра регуляризации, с которым невязка приблизительно равна сумме погрешностей измерений (т. е. заданий правой части) и аппроксимации (погрешности, заложенной в матрице
А).
Листинг 6.17. Квазиоптимальный выбор параметра регуляризации
(продолжение листинга 6.16)


Рис. 6.12. Исходный сигнал Y и его регуляризованная реконструкция (продолжение листинга 6.17)