Глава 9.1. О постановке задач

Начнем разговор об обыкновенных дифференциальных уравнениях с формулировки типичных задач, сопровождая вопросы их постановки конкретными примерами. При этом мы будем, несколько забегая вперед, приводить их решение, не обсуждая особенностей его отыскания средствами Mathcad.

Глава 9.1.1. Задачи Коши для ОДУ

Дифференциальные уравнения — это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают соотношения между искомыми функциями и их производными. Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными. В противном случае говорят об уравнениях в частных производных (см. главу II). Таким образом, решить (иногда говорят проинтегрировать) дифференциальное уравнение — значит, определить неизвестную функцию на определенном интервале изменения ее переменных.

ОДУ с неизвестной функцией у (t), в которое входят производные этой функции вплоть до y^(N) (t), называется ОДУN-го порядка. В частности, уравнение первого порядка может по определению содержать помимо самой искомой функции y(t) только ее первую производную у'(t), второго порядка— у' (t) и у'' (t) и т. д. В подавляющем большинстве практических случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши): у'(t)=f (у (t) ,t). Уравнение второго порядка может содержать, помимо самой функции, ее первую и вторую производные и т. д. Листинг 9.1 демонстрирует решение простого ОДУ второго порядка, описывающего модель затухающего гармонического осциллятора. Само уравнение приведено во второй строке листинга, после задания параметров модели, а вычисленный результат, т. е. искомая функция у (t), показан на рис. 9.1.

ПРИМЕЧАНИЕ

Модель гармонического осциллятора описывает, в частности, колебания маятника: y(t) описывает изменения угла его отклонения от вертикали, у' (t) — угловую скорость маятника, у" (t) — ускорение, а начальные условия, соответственно, начальное отклонение маятника у (0) =1.0 и начальную скорость у' (0)=0. Важно отметить, что модель является линейной, т.е. неизвестная функция (и ее производные) входят в уравнение в первой степени.

Листинг 9.1. Решение задачи Коши для ОДУ второго порядка (модель затухающего гармонического осциллятора)

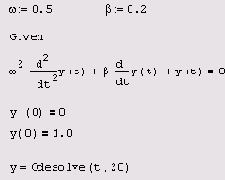
Как показывает листинг 9.1, помимо самого уравнения потребовалось определить два начальных условия (третья и четвертая строки листинга) — начальные значения y(t) и у' (t) при t=0. Вообще говоря, ОДУ (или система ОДУ) имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия. В соответствующих курсах высшей математики доказываются теоремы о существовании и единственности решения в зависимости от тех или иных условий.

Рис. 9.1. Решение уравнения w²у"+βу'+у=0 (продолжение листинга 9.1)

Имеются два типа задач, которые возможно решать с помощью Mathcad:

 задачи Коши — для которых определены начальные условия на искомые функции, т. е. заданы значения этих функций в начальной точке интервала интегрирования уравнения (именно им и посвящена данная глава);  краевые задачи — для которых заданы определенные соотношения сразу на обеих границах интервала (они рассматриваются в главе 10).

Сказанное относится как к отдельным дифференциальным уравнениям (см. разд. 9.2), так и к системам ОДУ (см. разд. 9.3). Важно подчеркнуть, что Mathcad умеет решать только такие системы дифференциальных уравнений, которые могут быть представлены в стандартной форме (форме Коши). Для неизвестных функций у₀ (t), y₁(t), ..., y_N-1(t) система ОДУ должна быть записана в форме:

что эквивалентно следующему векторному представлению:

Y' (t)=F(Y(t) ,t). (9.2)

Здесь Y и Y' — соответствующие неизвестные векторные функции переменной t размера Nx1, a F — векторная функция того же размера и количества переменных (N+1) (N компонент вектора и, возможно, t). Именно векторное представление (9.2) используется для ввода системы ОДУ в среде Mathcad.

Для того чтобы определить задачу Коши для системы из N ОДУ первого порядка, следует определить еще ровно N начальных условий, задающих значение каждой из функций yi(t0) в начальной точке интегрирования системы t0. В векторной форме они могут быть записаны в виде

Y(t0)=B, (9.3)

где B— вектор начальных условий размера Nx1, составленный из y_i(t0). Обратите внимание на необходимость векторной записи как самого уравнения, так и начального условия. В случае одного ОДУ первого порядка соответствующие векторы имеют только один элемент, а в случае системы N>1 уравнений — N.

Стандартные процедуры Mathcad применимы для систем ОДУ первого порядка, записанных в форме (9.2)—(9.3). Тем не менее, если в систему входят и уравнения высших порядков, то ее можно свести к системе большего числа уравнений первого порядка. Рассмотрим в качестве примера уравнение второго порядка модели осциллятора w²у'+βу'+у=0, решенное в листинге 9.1. Если ввести обозначение y₀(t)=y(t), yi(t)=y' (t), то уравнение сведется к эквивалентной системе:

y0(t)=y₁(t);

w²у₁'+βу'+у=0,

форма которой удовлетворяет форме (9.2) и уравнение может быть решено средствами Mathcad, предназначенными для систем ОДУ. Именно эта система решена ниже в листинге 9.3 (см. разд. 9.3.1). Отметим, что на рис. 9.1 показаны как зависимость у (t), так и у₁ (t)=y' (t).

Глава 9.1.2. Фазовый портрет динамической системы

Модели, основанные на задачах Коши для ОДУ, часто называют динамическими системами, подчеркивая, что, как правило, они содержат производные по времени t и описывают динамику некоторых параметров. Проблемы, связанные с динамическими системами, на самом деле весьма разнообразны и зачастую не сводятся к простому интегрированию ОДУ. Некоторые из них мы обозначим в данном разделе, отметив, что для изучения динамических систем центральным моментом является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий.

Решение ОДУ часто удобнее изображать не в виде графика у₀ (t), y₁(t), ..., как на рис. 9.1, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций. При таком построении графика аргумент t будет присутствовать на нем лишь параметрически. В рассматриваемом случае двух ОДУ (мы свели к ним в предыдущем разделе дифференциальное уравнение осциллятора второго порядка) фазовое пространство является координатной плоскостью, а решение представляет собой кривую, или, по-другому, траекторию, выходящую из точки, координаты которой равны начальным условиям (рис. 9.2). В общем случае, если система состоит из N ОДУ, то фазовое пространство является N-мерным. При N>3 наглядность теряется, и для визуализации фазового пространства приходится строить его различные проекции или прибегать к другим специальным приемам (например, отображению Пуанкаре).

Рис. 9.2. Решение уравнения w²у' '+βу'+у=0 на фазовой плоскости (продолжение листинга 9.1)

Как правило, решение задач Коши для ОДУ и их систем — задача хорошо разработанная и с вычислительной точки зрения довольно простая. На практике чаще встречаются другие, более сложные задачи, в частности, исследование поведения динамической системы в зависимости от начальных условий. При этом в большинстве случаев бывает необходимым изучить только асимптотическое решение ОДУ, т.е. y(t->∞), называемое аттрактором. Очень наглядным образом можно визуализировать такую информацию на фазовой плоскости, во многом благодаря тому, что существует всего несколько типов аттракторов, и для них можно построить четкую классификацию.

С одной стороны, каждое решение будет выходить из точки, координаты которой являются начальными условиями, но, оказывается, для большинства ОДУ целые семейства траекторий будут заканчиваться в одних и тех же аттракторах (стационарных точках или предельных циклах). Множество решений, вычисленное для всевозможных начальных условий, образует фазовый портрет динамической системы. С вычислительной точки зрения задача исследования фазового портрета часто сводится к обычному сканированию семейств решений ОДУ при разных начальных условиях.

ПРИМЕЧАНИЕ

Для рассматриваемого примера модели гармонического осциллятора имеется единственная стационарная точка (аттрактор), на которую "накручивается" решение, из каких бы начальных условий оно ни выходило. В теории динамических систем аттрактор такого типа называется фокусом.

Дальнейшее усложнение задач анализа фазовых портретов связано с их зависимостью от параметров, входящих в систему ОДУ. В частности, при плавном изменении параметра модели может меняться расположение аттракторов на фазовой плоскости, а также могут возникать новые аттракторы и прекращать свое существование старые. В первом случае, при отсутствии особенностей, будет происходить простое перемещение аттракторов по фазовой плоскости (без изменения их типов и количества), а во втором — фазовый портрет динамической системы будет коренным образом перестраиваться. Критическое сочетание параметров, при которых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации.

Поясним понятие бифуркации на примере той же модели осциллятора, которая зависит от двух параметров (ш и р). При р>о существует единственная стационарная точка типа фокуса (см. рис. 9.2), которая в точке бифуркации Р=о вырождается в аттрактор типа центр, характеризующийся тем, что решения ОДУ представляют собой циклы, совершаемые вокруг этой точки с амплитудой, которая существенно зависит от начальных условий (рис. 9.3). Для надежного исследования фазового портрета практически всегда необходимо решить систему ОДУ большое количество раз с самыми разными начальными условиями (и, возможно, с разным набором параметров модели), чтобы посмотреть, к каким аттракторам сходятся различные траектории.

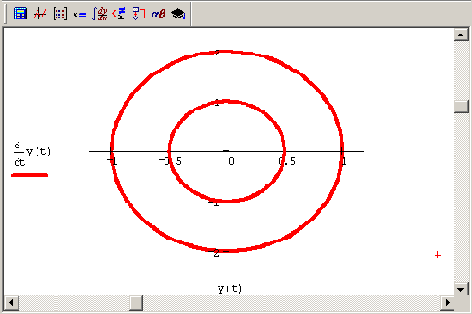
Рис. 9.3. Решение уравнения со2-у' '+у=0 для различных начальных условий (коллаж графиков)

Резюмируя содержание вводного раздела главы, перечислим еще раз типичные постановки задач, характерные для динамических систем:

 решение одной задачи Коши для ОДУ;  исследование фазового портрета (поиск аттракторов);  отыскание зависимости положения аттракторов в фазовом пространстве от параметров модели и фиксация бифуркационных значений параметров.

В дальнейших разделах этой главы при рассказе о возможностях Mathcad мы будем в первую очередь описывать решение первой (базовой) задачи, для которой предусмотрен целый арсенал средств. А именно: вычислительный блок для решения ОДУ (см. разд. 9.2), несколько встроенных функций для решения систем ОДУ (см. разд. 9.3), в том числе жестких, которые не поддаются решению стандартными методами (см. разд. 9.4). Приемы, которые автор рекомендует в качестве идиом решения остальных задач, будут рассмотрены эпизодически, на конкретных примерах классических динамических систем вычислительной физики, химии и биологии (см. разд. 9.5 и 9.4.3), связанных с динамическими системами. В частности, программа для визуализации фазового портрета рассмотрена в конце главы, на примере модели брюсселятора (см. разд. 9.5.4). Сводка алгоритмов с рекомендациями по их применению в зависимости от типа задачи приведена конспективно, без детального разбора (см. разд. 9.3.4).

Глава 9.2. Дифференциальное уравнение N-го порядка

Для решения ОДУ порядка N>1 в Mathcad предусмотрены две возможности:

 вычислительный блок Given/odesolve (начиная с версии 2000) — в этом случае решение имеет вид функции от t;  встроенные функции решения систем ОДУ, причем уравнения высших порядков необходимо предварительно свести к эквивалентной системе уравнений первого порядка, как об этом рассказано в разд. 9.1.1, — в этом случае решение имеет формат вектора.

В данном разделе рассматривается первый из вариантов, а второй будет описан в следующем, применительно к общему случаю системы N уравнений. Заметим лишь, что первый путь предпочтительнее из соображений наглядности представления задачи и результатов, а второй дает пользователю больше рычагов воздействия на параметры численного метода.

Вычислительный блок для решения ОДУ, реализующий численный метод Рунге—Кутты, состоит из трех частей:

 Given — ключевое слово;  ОДУ и начальные условия в формате y(t0)=b, записанные с помощью логических операторов, которые должны набираться на панели инструментов Boolean (Булевы операторы);  odesoive(t,ti) — встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1), причем t0<t1.

ПРИМЕЧАНИЕ 1

На запись ОДУ в пределах вычислительного блока накладывается несколько ограничений. Во-первых, ОДУ должно быть линейно относительно старшей производной, т. е. фактически должно быть поставлено в стандартной форме. Во-вторых, начальные условия должны иметь форму у (t0) =b или y(N) (t0) =b, а не более сложную (как, например, встречающаяся в некоторых математических приложениях форма у (t0)+y' (t0)=b).

ПРИМЕЧАНИЕ 2

Допустимо, и даже часто предпочтительнее, задание функции Odesoive (t,t1, step) с тремя параметрами, где step— внутренний параметр численного метода, определяющий количество шагов в которых метод Рунге—Кутты будет рассчитывать решение дифференциального уравнения. Чем больше step, тем с лучшей точностью будет получен результат, но тем больше времени будет затрачено на его поиск. Помните, что подбором этого параметра можно заметно (в несколько раз) ускорить расчеты без существенного ухудшения их точности.

Пример решения задачи Коши для ОДУ второго порядка, являющегося усложнением модели из листинга 9.1 на нелинейный случай (с параметром квадратичной нелинейности у)> приведен в листинге 9.2, а результат — на рис. 9.4. Учтите, что символ производной допускается вводить как средствами панели Calculus (Вычисления), как это сделано в листинге 9.1, так и в виде штриха, набрав его с помощью сочетания клавиш <Ctrl>+<F7> (как в листинге 9.2). Выбирайте тот или иной способ представления производной из соображений наглядности представления результатов — на ход расчетов он не влияет.

Рис. 9.4. Решение уравнения w2у''+βу '+у+γу²=0 (продолжение листинга 9.2)

Еще раз подчеркнем, что результатом применения блока Given/odesolve является функция y(t), определенная на промежутке (to,ti). Следует воспользоваться обычными средствами Mathcad, чтобы построить ее график или получить значение функции в какой-либо точке указанного интервала, например: у(10)=0.048.

Листинг 9.2. решение задачи Коши для ОДУ второго порядка (модель нелинейного осциллятора)

Пользователь имеет возможность выбирать между двумя модификациями численного метода Рунге—Кутты. Для смены метода необходимо нажатием правой кнопки мыши на области функции odesoive вызвать контекстное меню и выбрать в нем один из трех пунктов: Fixed (С фиксированным шагом), Adaptive (Адаптивный) или Stiff (Для жестких ОДУ). Подробнее о различиях этих методов сказано в разд. 9.3.4 и 9.4.

Глава 9.3. Система N дифференциальных уравнений

При помощи Mathcad можно решать системы N>1 ОДУ первого порядка, если они записаны в стандартной форме (Коши) в виде векторного соотношения: Y' (t)=F(Y(t),t) (см. разд. 9.1. 1).

Глава 9.3.1. Встроенные функции для решения систем ОДУ

В Mathcad имеется несколько встроенных функций, которые позволяют решать задачу Коши различными численными методами. Для "хороших" нежестких систем ОДУ применяются следующие функции:

 rkfixed(y0, t0, t1,M,D) — метод Рунге—Кутты с фиксированным шагом;  Rkadapt (y0,t0, t1,M,D) — метод Рунге—Кутты с переменным шагом;  Buistoer(y0,t0,t0,M,D) — метод Булирша—Штера;

 у0 — вектор начальных значений в точке t0 размера NXI;  t0 — начальная точка расчета;  t1 — конечная точка расчета;  M — число шагов, на которых численный метод находит решение;  D— векторная функция размера Nx1 двух аргументов — скалярного t и векторного у. При этом у — искомая векторная функция аргумента t того же размера Nx1.

ВНИМАНИЕ!

Соблюдайте регистр первой буквы рассматриваемых функций, поскольку это влияет на выбор алгоритма счета, в отличие от многих других встроенных функций Mathcad, например, Find=f ind (см. разд. 9.3.2).

Каждая из приведенных функций выдает решение в виде матрицы размера (M+1)х(N+1). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных N столбцах — значения искомых функций y0(t) ,y1(t), ... ,yN-i(t), рассчитанные для этих значений аргумента (рис. 9.5). Поскольку всего точек (помимо начальной) м, то строк в матрице решения будет всего M+1.

В листинге 9.3 приведен пример решения той же самой системы ОДУ осциллятора с затуханием (см. разд. 9.1 и 9.2) при помощи первой из функций rkfixed. Результат расчетов представлен на рис. 9.5 как содержимое матрицы и на рис. 9.6 в виде графика. Точки, в которых получено решение, отмечены на графике рис. 9.6 кружками. Чтобы использовать другой численный алгоритм, достаточно поменять имя функции rkfixed в последней строке листинга на другое (на практике как раз более эффективны функции Rkadapt и Bulstoer).

Листинг 9.3. Решение системы двух ОДУ(модель осциллятора)

Рис. 9.5. Результат, выдаваемый встроенной функцией в качестве решения системы ОДУ (продолжение листинга 9.3}

Первая строка листинга представляет задание параметров модели, вторая — начального условия задачи Коши, а в третьей строке листинга определено число шагов, на которых рассчитывается решение. Самая важная — это предпоследняя строка листинга, в которой, собственно, определяется система ОДУ. Последняя строка присваивает матричной переменной и результат действия функции rkfixed. Решение системы ОДУ будет осуществлено на промежутке (0,40).

Сравните рассматриваемую систему (см. разд. 9.1.Т), записанную в стандартной форме с формальной ее записью в Mathcad, чтобы не делать впоследствии ошибок. Во-первых, функция D, входящая в число параметров встроенных функций для решения ОДУ, должна быть функцией обязательно двух аргументов. Во-вторых, второй ее аргумент должен быть вектором того же размера, что и сама функция о. В-третьих, точно такой же размер должен быть и у вектора начальных значений у0. Не забывайте, что векторную функцию D(t,y) следует определять через компоненты вектора у с помощью кнопки Subscript (Нижний индекс) с наборной панели Calculator (Калькулятор) или нажатием клавиши <[>.

Матрица, представляющая решение, показана на рис. 9.5. Размер полученной матрицы будет равен (M+i)x(N+l), т. е. 51x3. Просмотреть все компоненты матрицы и, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки. Как нетрудно сообразить, на этом рисунке отмечены выделением расчетные значения искомых векторов на 10-м шаге. Это соответствует, с математической точки зрения, найденным значениям уо(8.0)=о. 307 и yi (8.0) =0.204. Для вычисления элементов решения в последней точке интервала используйте вывод элемента ин, ь Для построения графика решения надо отложить соответствующие компоненты матрицы решения по координатным осям: значения аргумента и<0> — вдоль оси х, а u^<1> и u^<2> — вдоль оси Y (рис. 9.6).

Рис. 9.6. График решения системы ОДУ осциллятора (продолжение листинга 9.3)

ВНИМАНИЕ!

Обратите внимание на некоторое разночтение в обозначении индексов вектора начальных условий и матрицы решения. В ее первом столбце собраны значения нулевой компоненты искомого вектора, во втором столбце — первой компоненты и т. д.

Глава 9.3.2. Решение одного уравнения (N=1)

Метод решения ОДУ при помощи встроенных функций rkfixed, Rkadapt или Bulstoer (в противоположность вычислительному блоку Given/ odesoive) сохранился с прежних версий Mathcad (до 2000-й). В большинстве случаев лучше использовать вычислительный блок Given/odesolve, который выигрывает в простоте и в наглядности, однако иногда предпочтительнее решать ОДУ первого порядка с помощью второго способа, например, при следующих обстоятельствах:

 вы работаете одновременно с более старыми (до 2001-й включительно) версиями Mathcad и хотите, чтобы ваши документы воспринимались каждой из них корректно;  одно ОДУ решается в контексте решения более сложных задач, в которые входят системы дифференциальных уравнений (для которых вычислительный блок неприменим) — в этом случае может потребоваться единый стиль программирования;  ответ предпочтительнее получить в виде вектора, а не функции;
вы привыкли к записи ОДУ в старых версиях Mathcad, у вас много документов, созданных с их помощью, и т. п.

Поскольку решение вторым способом одного ОДУ не отличается от решения систем ОДУ (см. предыдущий разд.), приведем пример его использования (листинг 9.4) практически без комментариев. Отметим лишь в случае одного ОДУ, что как само уравнение, так и начальное условие можно задавать не в векторной, а в скалярной форме. Результат выдается в виде матрицы размерности мх2, которая состоит из двух столбцов: в одном находятся значения аргумента t (от t0 до t1 включительно), а в другом соответствующие значения искомой функции у (t).

Рис. 9.7. Решение уравнения у'=1-у2 (продолжение листинга 9.4)

Построение графика (рис. 9.7) осуществляется так же, как и в рассмотренном в предыдущем разделе случае N уравнений, при помощи выделения столбцов из матрицы решения посредством оператора <>

Листинг 9.4. Решение задачи Коши для ОДУ первого порядка.

Глава 9.3.3. Решение систем ОДУ в одной заданной точке

Зачастую при решении дифференциальных уравнений требуется определить значения искомых функций не на всем интервале (t0.t1), а только в одной его последней точке. Например, весьма распространены задачи поиска аттракторов динамических систем. Известно, что для широкого класса ОДУ одна и та же система при разных (или даже любых, как рассмотренный выше пример осциллятора с затуханием) начальных условиях при t->∞ приходит в одну и ту же точку (аттрактор). Поэтому часто нужно определить именно эту точку.

Такая задача требует меньше ресурсов компьютера, чем решение системы ОДУ на всем интервале, поэтому в Mathcad имеются модификации встроенных функций Rkadapt и Buistoer. Они имеют несколько другой набор параметров и работают значительно быстрее своих аналогов:

 rkadapt (y0, t0, t1, асc, D, k, s) — метод Рунге—Кутты с переменным шагом;  buistoer (y0,t0, t1,acc,D,k,s) — метод Булирша— Штера:

 y0 — вектор начальных значений в точке t0;  t0,t1 — начальная и конечная точки расчета;  асc — погрешность вычисления (чем она меньше, тем с лучшей точностью будет найдено решение; рекомендуется выбирать значения погрешности в районе 0.001);  D — векторная функция, задающая систему ОДУ;  k — максимальное число шагов, на которых численный метод будет находить решение;  s — минимально допустимая величина шага.

Как легко заметить, вместо числа шагов на интервале интегрирования ОДУ в этих функциях необходимо задать точность расчета численным методом значения функций в последней точке. В этом смысле параметр асе похож на константу TOL, которая влияет на большинство встроенных численных алгоритмов Mathcad. Количество шагов и их расположение определяются численным методом автоматически, чтобы обеспечить эту точность. Два последних параметра нужны для того, чтобы пользователь мог искусственно повлиять на разбиение интервала на шаги. Параметр к служит для того, чтобы шагов не было чрезмерно много, причем нельзя сделать k>1000. Параметр s — для того, чтобы ни один шаг не был слишком малым для появления больших погрешностей при разностной аппроксимации дифференциальных уравнений внутри алгоритма. Эти параметры следует задавать явно, исходя из свойств конкретной системы ОДУ. Как правило, проведя ряд тестовых расчетов, можно подобрать их оптимальный набор для каждого конкретного случая.

Пример использования функции buistoer для той же модели линейного осциллятора приведен в листинге 9.5. В его первых двух строках, как обычно, определяется система уравнений и начальные условия; в следующей строке матрице и присваивается решение, полученное с помощью buistoer. Структура этой матрицы в точности такая же, как и в случае решения системы ОДУ посредством уже рассмотренных нами ранее встроенных функций (см. разд. 9.3.1). Однако в данном случае нам интересна только последняя точка интервала. Поскольку сделанное численным методом количество шагов, т. е. размер матрицы и, заранее неизвестно, то его необходимо предварительно определить. Это сделано в четвертой строке листинга, присваивающей это число переменной м, в этой же строке оно выведено на экран. В предпоследней строке листинга осуществлен вывод решения системы ОДУ на конце интервала, т. е. в точке t=s0 в виде вектора. В последней строке для примера еще раз выводится искомое значение первой функции из системы ОДУ (сравните его с соответствующим местом вектора из предыдущей строки). Чтобы попробовать альтернативный численный метод, достаточно в листинге 9.5 заменить имя функции buistoer на rkadapt.

Листинг 9.5. Поиск аттрактора системы двух ОДУ модели осциллятора

ВНИМАНИЕ!

Функции bulstoer и rkadapt (те, что пишутся со строчной буквы) не предназначены для нахождения решения в промежуточных точках интервала, хотя они и выдают их в матрице-результате.

Глава 9.3.4. О численных методах

В завершение раздела сделаем несколько важных замечаний относительно выбора численного алгоритма решения ОДУ и задания его параметров. Они не претендуют на общность, но, надеемся, будут весьма полезны читателю, особенно в случае возникновения проблем.

Рекомендации по выбору численного алгоритма

Все численные методы решения ОДУ основаны на аппроксимации дифференциальных уравнений разностными аналогами. В зависимости от конкретной формы аппроксимации получаются алгоритмы различной точности и быстродействия. В Mathcad использован наиболее популярный алгоритм Рунге—Кутты четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем. Поэтому в большинстве случаев стоит применять функцию rkfixed. Если по различным причинам время расчетов становится критичным или точность неудовлетворительна, стоит попробовать вместо rkfixed другие функции, тем более, что сделать это очень просто благодаря одинаковому набору параметров. Для этого нужно только поменять имя функции в программе.

Функция Rkadapt может быть полезна в случае, когда известно, что решение на рассматриваемом интервале меняется слабо либо существуют участки медленных и быстрых его изменений. Метод Рунге—Кутты с переменным шагом разбивает интервал не на равномерные шаги, а более оптимальным способом. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений — частыми. В результате для достижения одинаковой точности требуется меньшее число шагов, чем для rkfixed. Метод Булирша— Штера Buistoer часто оказывается более эффективным для поиска гладких решений.

Имея в виду сделанные замечания, приведем краткую сводку алгоритмов решения задач Коши для ОДУ, отмечая, какие из встроенных функций следует использовать в конкретных случаях.

 Для решения единственного уравнения (любого порядка) используйте вычислительный блок Given/Odesolve.  Для стандартных нежестких систем используйте алгоритм Булирша— Штера Buistoer.  Для систем с участками быстро и медленно меняющихся решений используйте адаптивный алгоритм Рунге—Кутты Rkadapt.  В учебных целях и для решения несложных задач можно использовать алгоритм Рунге—Кутты с фиксированным шагом Rkfixed.  Для получения решения в одной конечной точке интервала используйте (в зависимости от перечисленных классов задач) одну из встроенных функций с именем, начинающимся со строчной буквы.  Для жестких систем (см. разд. 9.4) используйте функции Radau stiffb или stiffr, причем если вы затрудняетесь с вводом якобиана, применяйте первую из них).

Мы не будем в этой книге приводить описание численных алгоритмов, поскольку им посвящено огромное количество книг, и читатель, несомненно, найдет соответствующую литературу с подробным объяснением их работы. Тем не менее, разберем несколько важных моментов, касающихся выбора алгоритма и его параметров.

Число шагов

Все встроенные функции требуют задания для численного метода количества шагов, разбивающих интервал интегрирования ОДУ. Это очень важный параметр, непосредственно влияющий на погрешность результата и скорость расчетов. При решении систем ОДУ многие проблемы могут быть устранены при помощи простой попытки увеличить число шагов численного метода. В частности, сделайте так при неожиданном возникновении ошибки "Found a number with a magnitude greater than 10^307" (Найдено число, превышающее значение 10307). Данная ошибка не обязательно говорит о том, что решение в действительности расходится, а возникает из-за недостатка шагов для корректной работы численного алгоритма.

В качестве иллюстрации приведем результаты простых расчетов (листинг 9.6), в которых определяется пользовательская функция и(м>, представляющая решение ОДУ в зависимости от числа шагов м. На рис. 9.8 показано несколько графиков решения системы ОДУ затухающего линейного осциллятора для нескольких значений м.

Рис. 9.8. Решение системы ОДУ в зависимости от числа узлов М (продолжение листинга 9.6)

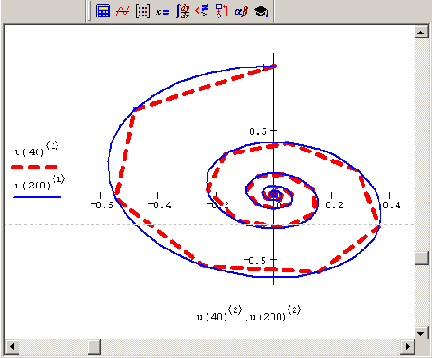
Рис. 9.9. Фазовый портрет решения системы ОДУ при М=40 и М=200 (продолжение листинга 9.6)

Как можно заметить, несмотря на, в целом, правильное решение ОДУ в узлах (оно показано кружками и квадратами), профиль решения при малых м получается неверным. Еще лучше это видно на рис. 9.9, представляющем фазовый портрет системы с разным числом шагов. Видно, что для м=200 решение получается более гладким (конечно, при этом увеличивается и время расчетов).

Листинг 9.6. Решение системы ОДУ как функции числа шагов

Погрешность алгоритмов решения ОДУ в точке

Обратимся теперь к функциям buistoer и rkadapt (тем, что пишутся со строчной буквы), которые предназначены для нахождения решения в определенной точке интервала интегрирования системы ОДУ. В первую очередь, подчеркнем еще раз, что их нельзя применять для получения решения в промежуточных точках интервала, несмотря на их вывод в матрице-результате. На рис. 9.10 показан фазовый портрет системы ОДУ динамической модели осциллятора, полученный при помощи функции buistoer в  листинге 9.5 (см. разд. 9.3.3) и с помощью rkadapt (при соответствующей замене третьей строки листинга 9.5). Видно, что, несмотря на высокую точность, равную 10^-5, и верный результат на конце интервала, график, полученный при помощи функции buistoer (рис. 9.10, а), мало напоминает правильный фазовый портрет (см. рис. 9.9), начиная быть приемлемым только при предельно допустимом для обсуждаемых функций значении асс=10^-16. В данном случае конкретной системы ОДУ функция rkadapt дает качественно верное решение (рис. 9.10, б), однако его необходимая точность обеспечивается только в последней точке временного интервала.

В заключение остановимся на влиянии выбора параметра асе на расчеты. Как правило, разные численные методы работают несколько по-разному. Алгоритм Рунге—Кутты дает результат тем ближе к истинному, чем меньше выбирается параметр асе, а Булирша—Штера часто демонстрирует менее естественную зависимость у(е): даже при относительно больших е реальная погрешность остается хорошей (намного лучше метода Рунге—Кутты).

Рис. 9.10. Фазовый портрет, полученный bulstoer (a) и rkadapt (б) (продолжение листинга 9.5)

Поэтому для экономии времени расчетов в функции buistoer можно выбирать и большие асе.

Чтобы обеспечить заданную точность, данные алгоритмы могут изменять как количество шагов, разбивающих интервал (t0,t1), так и их расположение вдоль интервала. Чтобы выяснить, на сколько шагов разбивался интервал при расчетах, воспользуемся простой программой, представленной в листинге 9.7. В ней определены пользовательские функции R(е) и B(е), вычисляющие для конкретной задачи (методов Рунге—Кутты и Булирша—Штера соответственно) зависимость числа шагов (т. е. числа строк получающейся матрицы) от параметра е=асс. Графики функций R(e) и B(е) показаны на рис. 9.11. Как видно, методу Рунге—Кутты при увеличении требуемой точности требуется все возрастающее количество шагов (и, соответственно, времени на расчеты), в противоположность методу Булирша—Штера, демонстрирующему большую экономичность.

ПРИМЕЧАНИЕ

Максимальное количество шагов алгоритма ограничивается еще одним параметром k встроенных функций buistoer и rkadapt (с/и. рази 9.3.3).

Листинг 9.7. Число шагов адаптивного численного алгоритма в зависимости от погрешности acc

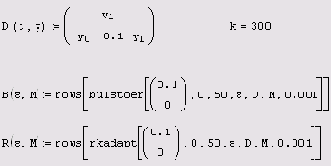
Таким образом, проводя тестовые расчеты для различных задач и подбирая наилучший набор параметров, можно существенно сэкономить ресурсы компьютера. Конечно, проводить подобный анализ стоит в случаях, когда время расчетов для вас критично.

Рис. 9.11. Зависимость числа шагов от параметра асе численных методов (продолжение листинга 9.7)

Глава 9.4. Жесткие системы ОДУ

До сих пор мы имели дело с "хорошими" уравнениями, которые надежно решались численными методами Рунге—Кутты. Однако имеется класс так называемых жестких (stiff) систем ОДУ, для которых стандартные методы практически неприменимы, поскольку их решение требует исключительно малого значения шага численного метода. Некоторые из специальных алгоритмов, разработанных для этих систем, реализованы в Mathcad.

Глава 9.4.1. Что такое жесткие ОДУ?

Исторически интерес к жестким системам возник в середине XX в. при изучении уравнений химической кинетики с одновременным присутствием очень медленно и очень быстро протекающих химических реакций (оно будет рассмотрено в разд. 9.4.3). Тогда неожиданно оказалось, что считавшиеся исключительно надежными методы Рунге—Кутты стали давать сбой при расчете этих задач.

Строгого общепринятого математического определения жестких ОДУ нет. В рамках этой книги будем считать, что жесткие системы — это те уравнения, решение которых получить намного проще с помощью определенных неявных методов, чем с помощью явных методов (типа тех, что были рассмотрены в предыдущих разделах). Примерно такое определение было предложено в 1950-х гг. классиками в этой области Кертиссом и Хиршфельдером. Начнем разговор о жестких ОДУ с примера нежесткого уравнения (листинг 9.8), решение которого удается получить численным методом Рунге— Кутты (рис. 9.12).

Листинг 9.8. Решение нежесткого ОДУ

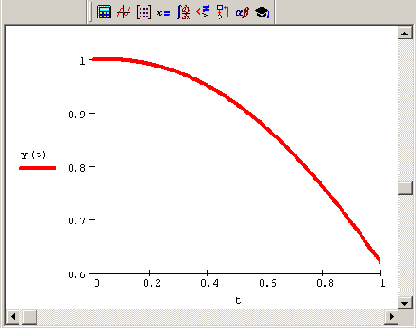
Рис. 9.12. Решение нежесткого ОДУ методом Рунге—Кутты (продолжение листинга 9.8)

Обратите внимание на значение коэффициента -10 во второй строке листинга. Если изменить его на -50, то решение меняется до неузнаваемости (рис. 9.13). Вас, несомненно, должен насторожить результат, выданный Mathcad. Характерная "разболтка" решения говорит о неустойчивости алгоритма. Первое, что можно сделать, — увеличить количество шагов в методе Рунге—Куттты. Для этого достаточно добавить третий параметр step в функцию odesoive (t, i,step). После нескольких экспериментов можно подобрать такое значение step, которое будет обеспечивать устойчивость решения. Читатель может самостоятельно убедиться, что при step>50 "разболтка" пропадает, и решение принимает вид графика, показанного ниже на рис. 9.14.

Рис. 9.13. Неверное решение более жесткого ОДУ методом Рунге—Кутты (листин 9.8 с коэффициентом -50)

Таким образом, во-первых, мы выяснили, что одни и те же уравнения с разными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 9.8 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.

ПРИМЕЧАНИЕ

Некоторые ученые замечают, что в последние годы методы Рунге—Кутты, считавшиеся ранее незыблемыми, стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.

Глава 9.4.2. Функции для решения жестких ОДУ

Решение жестких систем дифференциальных уравнений можно осуществить только с помощью встроенных функций, аналогичных по действию семейству рассмотренных выше функций для обычных ОДУ:

 Radau(y0,t0,t1,M,F) — алгоритм RADAUS для жестких систем ОДУ;  stiffb(y0,t0,1,M,F, J) — алгоритм Булирша—Штера для жестких систем ОДУ;  stiffr (y0, t0, t1,M, F, J) — алгоритм Розенброка для жестких систем ОДУ:

 у0 — вектор начальных значений в точке to;  t0,t1 — начальная и конечная точки расчета;  M — число шагов численного метода;  F — векторная функция F(t, у) размера 1xN, задающая систему ОДУ;  J — матричная функция j(t,y) размера (N+1)xN, составленная из вектора производных функции F(t,y) no t (правый столбец) и ее якобиана (N левых столбцов).

Как вы можете заметить, для двух последних функций серьезным отличием от функций, решающих нежесткие системы, является добавление к стандартному набору параметров дополнительной матричной функции, задающей якобиан системы ОДУ. Решение выдается в виде матрицы, по форме идентичной аналогичным функциям решения нежестких задач Коши.

ПРИМЕЧАНИЕ

Встроенная функция Radau, которая не требует явного задания якобиана системы уравнений, появилась в версии Mathcad 2001I, а остальные две — в Mathcad 2001.

Решение жесткой задачи из предыдущего раздела при помощи функции Radau приведено в листинге 9.9. Результат показан в виде графика на рис. 9.14 вместе с графиком решения менее жесткой задачи (для которого применялся листинг 9.8). Как вы видите, хватило всего пяти точек разбиения интервала интегрирования жесткого ОДУ, чтобы метод с ним справился. Специфика применения других встроенных функций, требующих дополнительного задания якобиана, будет рассмотрена в следующем разделе на примере уравнения химической кинетики.

Листинг 9.9. Решение жесткого ОДУ алгоритмом RADAUS

Рис. 9.14. Решение жесткого ОДУ методом RADAUS (продолжение листингов 9.8 и 9.9)

В заключение приведем соответствующие встроенные функции, которые применяются для решения жестких систем ОДУ не на всем интервале, а только в одной заданной точке t1.

 radau(y0, t0, t1, асc, F, k, s) — метод RADAUS.  stiffb(y0,t0,t1,acc,F, J, k, s) — метод Булирша—Штера.  stiffr (y0,t0, t1, acc, F, J, k, s) — метод Розенброка.

Имена этих функций пишутся со строчной буквы, а их действие и набор параметров полностью аналогичны рассмотренным нами ранее для функций, относящихся к решению в заданной точке нежестких систем (см. разд. 9.3.2). Отличие заключается в специфике применяемого алгоритма и необходимости задания матричной функции якобиана J(t,y) (для двух последних функций).

Глава 9.4.3. Пример: химическая кинетика

Рассмотрим классическую модель химической кинетики (Робертсон, 1966), которая как нельзя лучше передает смысл понятия жесткости ОДУ.

Попытка решения стандартными методами

Рассмотрим составную схему химического взаимодействия трех веществ. Пусть вещество "О" медленно превращается в "1": "0"->"1" (со скоростью 0.1), вещество "1" при каталитическом воздействии самого себя превращается очень быстро в вещество "2": "1"+"1"->"2"+"1" (10³). И, наконец, подобным образом (но со средней скоростью) реагируют вещества "2" и "1": "1"+"2"->"0" + "2" (10²). Система ОДУ, описывающая динамику концентрации реагентов, с попыткой решения методом Рунге—Кутты, приведена, в символической форме в первой строке листинга 9.10.

Листинг 9.10. Жесткая система ОДУ химической кинетики

Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяет жесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции F(t,y), т.е. функциональную матрицу, составленную из производных F(t,y) (см. разд 3.4.3). Чем сильнее вырождена матрица Якоби, тем жестче система уравнений. В приведенном примере определитель якобиана и вовсе равен нулю при любых значениях у₀, y₁ и у₂ (листинг 9.11, вторая строка). В первой строке листинга 9.11 приведено напоминание способа вычисления якобиана средствами Mathcad на примере определения элементов его первой строки.

Листинг 9.11. Якобиан рассматриваемой системы ОДУ химической кинетики

Для примера, приведенного в листинге 9.10, стандартным методом Рунге— Кутты все-таки удается найти решение (оно показано на рис. 9.15). Однако для этого требуется очень большое число шагов, M=20000, что делает расчеты очень медленными. При меньшем числе шагов численному алгоритму не удается найти решение. В процессе работы алгоритма оно расходится, и Mathcad вместо результата выдает ошибку о превышении предельно большого числа.

Еще один факт, на который стоит обратить внимание, — это различие в порядке величины получающегося решения. Как видно из рис. 9.15, концентрация первого реагента уг существенно (в тысячи раз) превышает концентрацию остальных. Это свойство также очень характерно для жестких систем.

ПРИМЕЧАНИЕ

В принципе, можно было бы снизить жесткость системы "вручную", применяя масштабирование. Для этого нужно искусственно уменьшить искомую функцию у₁ к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие y₁, на 1000. После масштабирования для решения полученной системы методом Рунге—Кутты будет достаточно взять всего м=20 шагов. Соответствующий пример вы найдете на компакт-диске.

Рис. 9.15. Решение жесткой системы ОДУ химической кинетики методом Рунге—Кутты (продолжение листинга 9.10)

Применение специфических алгоритмов

Покажем действие этих алгоритмов на том же примере жесткой системы ОДУ химической кинетики (листинг 9.12). Обратите внимание, как следует представлять в данном случае якобиан, сравнив задание матричной функции в предпоследней строке листинга 9.12 с заданием якобиана из листинга 9.11.

Листинг 9.12. Решение жесткой системы ОДУ химической кинетики

Расчеты показывают, что для получения того же результата (который был изображен на рис. 9.15) оказалось достаточно в тысячу раз меньшего количества шагов численного алгоритма, чем для стандартного метода Рунге— Купы ! Примерно во столько же раз требуется меньше компьютерного времени на проведение расчетов. Стоит ли говорить, что, если вы имеете дело с жесткими (в той или иной степени) системами, применение описанных специальных алгоритмов просто необходимо.

Важно заметить, что до сих пор мы имели дело с примером не очень жесткой системы. Попробуйте вместо скоростей упомянутых химических реакций 0.1, 10³ и 10² взять другие числа, например, 0.05, 10⁴ и 10⁷ соответственно. Заметим, что такое соотношение скоростей часто встречается в прикладных задачах химической кинетики и определяет куда более жесткую систему ОДУ. Ее уже никак не удается решить стандартными методами, поскольку число шагов численного метода должно быть просто гигантским. А между тем алгоритмы для жестких ОДУ справляются с этой задачей с легкостью (рис. 9.16), причем практически при тех же значениях шага, что были взяты в листинге 9.12. Обратите внимание, что порядки величины решений для концентраций различных веществ на рис. 9.16 различаются еще сильнее, чем в предыдущем (менее жестком) примере.

Рис. 9.16. Решение более жесткой системы ОДУ химической кинетики методом Розенброка

Для решения очень жестких систем особенно подходит функция Radau, которая соблазнительна еще и тем, что избавляет от необходимости предварительного расчета якобиана. В случае очень жесткой задачи химической кинетики результат, выдаваемый функцией Radau, практически тот же, что и в случае использования алгоритма Розенброка (рис. 9.16). Любопытно, что решение менее жесткой системы (из предыдущего листинга) при помощи функции Radau удается получить только для первой половины интервала, примерно до t1=20. Для больших интервалов она дает сбой, выводя вместо решения сообщение об ошибке.

Глава 9.5. Примеры: классические динамические системы

В предыдущих разделах было использовано в качестве примера в основном линейное уравнение осциллятора (оно содержало только первую степень неизвестных функций и их производных). Между тем многие нелинейные уравнения демонстрируют совершенно удивительные свойства, причем решение большинства из них можно получить лишь численно.

Рассмотрим несколько наиболее известных классических примеров динамических систем, имея в виду, что читателю они могут пригодиться как в познавательных, так и в практических целях. Это модели динамики популяций (Вольтерры), генератора автоколебаний (Ван дер Поля), турбулентной конвекции (Лоренца) и химической реакции с диффузией (Пригожина). Как уже было сказано, для изучения динамических систем разработана специальная теория, центральным моментом которой является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий. 

ПРИМЕЧАНИЕ

В большинстве примеров, изложенных ниже, для построения схемы фазового портрета рассчитывается несколько решений для разных начальных условий. О, том, как проделать такие расчеты в Mathcad, будет рассказано ниже на примере модели брюсселятора (см. разд. 9.5.4).

Ограничимся в дальнейшем минимальными комментариями и приведем листинги и графики решений без подробного обсуждения.

Глава 9.5.1. Модели динамики биологических популяций

Модель взаимодействия "хищник—жертва" независимо предложили в 1925— 1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения (листинг 9.13) моделируют временную динамику численности двух биологических популяций жертвы уо и хищника уь Предполагается, что жертвы размножаются с постоянной скоростью с, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом г), и умирают естественным образом (смертность определяется константой о). В листинге рассчитываются три решения о, с, р для разных начальных условий.
Листинг 9.13. Модель "хищник-жертва"

Модель замечательна тем, что в такой системе наблюдаются циклическое увеличение и уменьшение численности и хищника (рис. 9.17), и жертвы, так часто наблюдаемое в природе. Фазовый портрет системы представляет собой концентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численности обеих популяций существенно зависят от начальных условий — после каждого периода колебаний система возвращается в ту же точку. Динамические системы с таким поведением называют негрубыми.

ПРИМЕЧАНИЕ

Пример негрубой системы (модель осциллятора без затухания) с особой точкой типа "центр" был нами рассмотрен ранее (см. разд. 9.1).

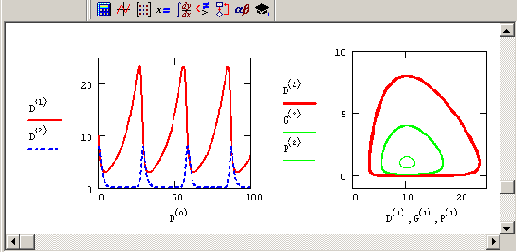
Рис. 9.17. График решения (слева) и фазовый портрет (справа) системы "хищник—жертва" (продолжение листинга 9.13)

Рассмотренную модель динамики двух популяций легко можно модифицировать, изменив тип взаимодействия "хищник—жертва" на тип конкуренции. Для этого надо учесть, что рост численности каждой популяции тормозит, во-первых, межвидовая, и, во-вторых, внутривидовая конкуренция.

В результате система (во второй строке листинга) запишется в виде:

где матрица г задает коэффициенты убывания численности вследствие конкурентной борьбы (диагональные элементы соответствуют внутри-, а недиагональные — межвидовой конкуренции).

График решения (для разных начальных условий) и фазовый портрет для описанной системы ОДУ показаны на рис. 9.18. Как видно, конкурентная борьба приводит к установлению некоторого стационарного состояния, выражающего равновесие видов. Особая точка, к которой стремится решение системы ОДУ подобным образом, называется узлом.

ПРИМЕЧАНИЕ

Соответствующий файл с программой вы найдете на компакт-диске, вместе с более простой моделью динамики одной популяции с внутривидовой конкуренцией (называемой логистической моделью).

Рис. 9.18. График решения (слева) и фазовый портрет (справа) модели конкуренции популяций

Глава 9.5.2. Автоколебания

Рассмотрим решение уравнения Ван дер Поля, описывающего электрические колебания в замкнутом контуре, состоящем из соединенных последовательно конденсатора, индуктивности, нелинейного сопротивления и элементов, обеспечивающих подкачку энергии извне (листинг 9.14). Неизвестная функция времени y(t) имеет смысл электрического тока, а в параметре ц заложены количественные соотношения между составляющими электрической цепи, в том числе и нелинейной компонентой сопротивления.

Листинг 9.14. Модель Ван дер Поля

Рис. 9.19. График решения (слева) и фазовый портрет (справа) уравнения Ван дер Поля (продолжение листинга 9.14)

Решением уравнения Ван дер Поля являются колебания, вид которых для µ=1 показан на рис. 9.19. Они называются автоколебаниями и принципиально отличаются от рассмотренных нами ранее (например, колебаний маятника в модели осциллятора или численности популяций в модели Вольтерpa) тем, что их характеристики (амплитуда, частота, спектр) не зависят от начальных условий, а определяются исключительно свойствами самой динамической системы. Через некоторое время расчетов после выхода из начальной точки решение выходит на один и тот же цикл колебаний, называемый предельным циклом. Аттрактор типа предельного цикла является замкнутой кривой на фазовой плоскости. К нему асимптотически притягиваются все окрестные траектории, выходящие из различных начальных точек, как изнутри (рис. 9.19), так и снаружи (рис. 9.20) предельного цикла.

ПРИМЕЧАНИЕ 1

Если компьютер у вас не самый производительный, то расчет в Mathcad фазового портрета с рис. 9.19, 9.20 может занять относительно продолжительное время, что связано с численным определением сначала решения y(t), а потом его производной. Время расчетов можно было бы существенно сократить, если использовать вместо вычислительного блока Given/odesolve одну из встроенных функций, которые выдают решение в виде матрицы, например, rkfixed.

ПРИМЕЧАНИЕ 2

По мере возрастания параметра µ модель Ван дер Поля становится все более жесткой. Например, при ц=5000 решение уже придется искать при помощи специфических методов решения жестких задач (см. разд. 9.3). Это еще раз доказывает, что одна и та же система ОДУ с различными коэффициентами может быть жесткой в разной степени.

Рис. 9.20. Решение уравнения Ван дер Поля при других начальных условиях у=-2, у' =-3

Глава 9.5.3. Странный аттрактор

Одна из самых знаменитых динамических систем предложена в 1963 г. Лоренцем в качестве упрощенной модели конвективных турбулентных движений жидкости в нагреваемом сосуде тороидальной формы. Система состоит из трех ОДУ и имеет три параметра модели (листинг 9.15). Поскольку неизвестных функций три, то фазовый портрет системы должен определяться не на плоскости, а в трехмерном пространстве.

Листинг 9.15. Модель Лоренца

Решением системы Лоренца при определенном сочетании параметров (рис. 9.21 и 9.22) является странный аттрактор (или аттрактор Лоренца) — притягивающее множество траекторий на фазовом пространстве, которое по виду идентично случайному процессу. В некотором смысле аттрактор Лоренца является стохастическими автоколебаниями, которые поддерживаются в динамической системе за счет внешнего источника.

Решение в виде странного аттрактора появляется только при некоторых сочетаниях параметров. В качестве примера на рис. 9.23 приведен результат для r=10 и тех же значений остальных параметров. Как видно, аттрактором в этом случае является фокус. Перестройка типа фазового портрета происходит в области промежуточных г. Критическое сочетание параметров, при которых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации. Физический смысл бифуркации в модели Лоренца, согласно современным представлениям, описывает переход ламинарного движения жидкости к турбулентному.

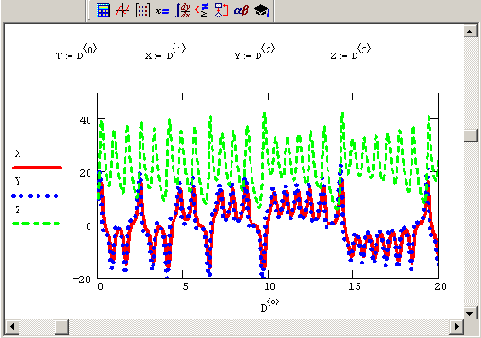
Рис. 9.21. Решение в виде аттрактора Лоренца (продолжение листинга 9.15)

Рис. 9.22. Аттрактор Лоренца на фазовой плоскости (продолжение листинга 9.15)

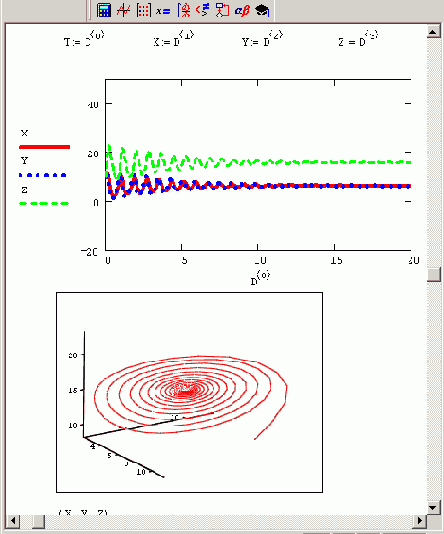
Рис. 9.23. Решение системы Лоренца с измененным параметром г=10

Замечательно, что решение подобных нелинейных динамических систем можно получить только численно, поэтому их изучение стало бурно развиваться с ростом возможностей вычислительной техники в последние полвека.

ПРИМЕЧАНИЕ 1

На компакт-диске вы найдете решение в виде странного аттрактора еще одной классической динамической системы (палеомагнетизм Рикитаке), моделирующей глобальное движение магнитных полюсов Земли.

ПРИМЕЧАНИЕ 2

Также на компакт-диске находится программа с реализацией алгоритма поиска отображения Пуанкаре (на примере модели Лоренца) — эффективного приема теории динамических систем.

Глава 9.5.4. Брюсселятор

До сих пор в этой главе в качестве примеров расчета динамических систем мы приводили графики 1—3 траекторий на фазовой плоскости. Однако для надежного исследования фазового портрета необходимо решить систему ОДУ большое количество раз с самыми разными начальными условиями (и, возможно, с разным набором параметров модели), чтобы посмотреть, к каким аттракторам сходятся различные траектории. В Mathcad можно реализовать эту задачу, например, в форме алгоритма, приведенного в листинre 9.16 для решения системы уравнений автокаталитической химической реакции с диффузией. Эта модель, называемая моделью брюсселятора, предложена в 1968 г. Лефевром и Пригожиным. Неизвестные функции отражают динамику концентрации промежуточных продуктов некоторой реальной химической реакции. Параметр модели в равен исходной концентрации катализатора.

Листинг 9.16. Построение фазового портрета для модели брюсселятора

Предложенный алгоритм формирует из отдельных матриц решений системы ОДУ с разными начальными условиями объединенную матрицу U. Пары начальных условий задаются в первой строке листинга в виде матрицы v размера 2х10. Последнее означает построение десяти траекторий. Для того чтобы поменять количество траекторий, измените соответствующим образом размер этой матрицы. Затем (рис. 9.24) элементы матрицы и выводятся на график в виде отдельных точек. Отсутствие соединения точек линиями является недостатком алгоритма, но это плата за возможность представить в Mathcad несложным образом сразу большое количество траекторий на фазовой плоскости.

Рис. 9.24. Фазовый портрет брюсселятора при В=0.5 (продолжение листинга 9.16)

Как видно из рис. 9.24, все траектории, вышедшие из разных точек, асимптотически стремятся к одному и тому же аттрактору (1,0.5). Из теории динамических систем нам известно, что такой аттрактор называется узлом (с узлом мы уже встречались в примере разд. 9.4.1). Конечно, в общем случае при анализе фазового портрета желательно "прощупать" большее число траекторий, задавая более широкий диапазон начальных условий. Не исключено, что в других областях фазовой плоскости траектории будут сходиться к другим аттракторам.

Эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром в. При его увеличении узел будет сначала постепенно смещаться в точку с координатами (1, в), пока не достигнет бифуркационного значения B=2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. При дальнейшем увеличении в происходит лишь количественное изменение параметров этого цикла. Решение, полученное при B=2.5, показано на рис. 9.25.

ПРИМЕЧАНИЕ

Чтобы найти аттракторы динамической системы, как известно, нужно решить систему алгебраических уравнений, получающуюся из системы ОДУ заменой нулями их левых частей. Эти задачи также удобно решать средствами Mathcad (см. главу 5). В частности, исследование зависимости фазового портрета от параметров системы ОДУ и поиск бифуркаций можно проводить методами продолжения (с/и. разд. 5.3.3).

Рис. 9.25. Фазовый портрет брюсселятора при В=2.5

Читатели, сталкивающиеся с расчетом динамических систем, несомненно, оценят возможности Mathcad по построению фазовых портретов и исследованию бифуркаций. Возможно также, что они найдут лучшие программные решения этой задачи, чем алгоритм, предложенный в данном разделе автором.

---

---