Глава 10.1.О постановке задач

Постановка краевых задач для ОДУ отличается от задач Коши, рассмотренных в главе 9, тем, что граничные условия для них ставятся не в одной начальной точке, а на обеих границах расчетного интервала. Если имеется система N обыкновенных дифференциальных уравнений первого порядка, то часть из N условий может быть поставлена на одной границе интервала, а оставшиеся условия — на противоположной границе.

ПРИМЕЧАНИЕ

Дифференциальные уравнения высших порядков можно свести к эквивалентной системе ОДУ первого порядка (см. главу 9).

Чтобы лучше понять, что из себя представляют краевые задачи, рассмотрим их постановочную часть на конкретном физическом примере модели взаимодействия встречных световых пучков. Предположим, что надо определить распределение интенсивности оптического излучения в пространстве между источником (лазером) и зеркалом, заполненном некоторой средой (рис. 10.1). Будем считать, что от зеркала отражается R-Я часть падающего излучения (т. е. его коэффициент отражения равен R), а среда как поглощает излучение с коэффициентом ослабления а(х), так и рассеивает его. Причем коэффициент рассеяния назад равен г(х). В этом случае закон изменения интенсивности у₀(х) излучения, распространяющегося вправо, и интенсивности y₁ (х) излучения влево определяется системой двух ОДУ первого порядка:

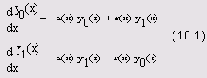
Для правильной постановки задачи требуется, помимо уравнений, задать такое же количество граничных условий. Одно из них будет выражать известную интенсивность излучения 10, падающего с левой границы х=0, а второе — закон отражения на его правой границе

x=1:

y0(0) = 10; (10.2)

y₁(l) = Rxy₀(l).

Рис. 10.1. Модель краевой задачи

Полученную задачу называют краевой (boundary value problem), поскольку условия поставлены не на одной, а на обеих границах интервала (0,1).  И, в связи с этим, их не решить методами предыдущей главы, предназначенными для задач с начальными условиями. Далее для показа возможностей Mathcad будем использовать этот пример с R=1 и конкретным видом a(x)=const=1 и r(x)=const=0.1, описывающим случай изотропного (не зависящего от координаты х) рассеяния.

ПРИМЕЧАНИЕ 1

Модель, представленная на рис. 10.1, привела к краевой задаче для системы линейных ОДУ. Она имеет аналитическое решение в виде комбинации экспонент. Более сложные, нелинейные, задачи возможно решить только численно. Нетрудно сообразить, что модель станет нелинейной, если сделать коэффициенты ослабления и рассеяния зависящими от интенсивности излучения. Физически это будет соответствовать изменению оптических свойств среды под действием мощного излучения.

ПРИМЕЧАНИЕ 2

Модель встречных световых пучков привела нас к системе уравнений (10.1), в которые входят производные только по одной переменной х. Если бы мы стали рассматривать более сложные эффекты рассеяния в стороны (а не только вперед и назад), то в уравнениях появились бы частные производные по другим пространственным переменным у и z. В этом случае получилась бы краевая задача для уравнений в частных производных, решение которой во много раз сложнее ОДУ.

Глава 10.2. Решение краевых задач средствами Mathcad

Для решения краевых задач в Mathcad реализован наиболее популярный алгоритм, называемый методом стрельбы или пристрелки (shooting method). Он, по сути, сводит решение краевой задачи к решению серии задач Коши с различными начальными условиями. Рассмотрим сначала основной принцип алгоритма стрельбы на примере модели световых пучков (см. рис. 10.1), а встроенные функции, реализующие этот алгоритм, приведем в следующем разделе.

Глава 10.2.1. Алгоритм стрельбы

Суть метода стрельбы заключается в пробном задании недостающих граничных условий на левой границе интервала и решении затем полученной задачи Коши хорошо известными методами (см. главу 11). В нашем примере не хватает начального условия для y₁(0), поэтому сначала зададим ему произвольное значение, например, у₁(0)=10. Конечно, такой выбор не совсем случаен, поскольку из физических соображений ясно, что, во-первых, интенсивность излучения — величина заведомо положительная, и, во-вторых, отраженное излучение должно быть намного меньше падающего. Решение задачи Коши с помощью функции rkfixed приведено в листинге 10.1, причем в его последней строке выведены расчетные значения у0 и уг на правой крайней точке интервала х=1. Разумеется, они не совпадают, т. е. правое краевое условие не выполнено, из чего следует, что полученный результат не является решением поставленной краевой задачи.

Листинг 10.1. Решение пробной задачи Коши для модели (10.1)

График полученных решений показан на рис. 10.2 (слева). Из него также видно, что взятое наугад второе начальное условие не обеспечило выполнение граничного условия при х=1. В целях лучшего выполнения этого граничного условия следует взять большее значение y₁(0), например, y₁(0)=15, и вновь решить задачу Коши. Соответствующий результат показан на том же рис. 10.2 (в центре). Граничное условие выполняется с лучшей точностью, но опять-таки оказалось недостаточным. Для еще одного значения y₁(0)=20 получается решение, показанное на рис. 10.2 (справа). Из сравнения двух правых графиков легко заключить, что недостающее начальное условие больше 15, но меньше 20. Продолжая подобным образом "пристрелку"  по недостающему начальному условию, возможно отыскать правильное решение краевой задачи.

В этом и состоит принцип алгоритма стрельбы. Выбирая пробные начальные условия (проводя пристрелку) и решая соответствующую серию задач Коши, можно найти то решение системы ОДУ, которое (с заданной точностью) удовлетворит граничному условию (или, в общем случае, условиям) на другой границе расчетного интервала.

Конечно, описанный алгоритм несложно запрограммировать самому, оформив его как решение системы заданных алгоритмически уравнений, выражающих граничные условия на второй границе, относительно неизвестных пристрелочных начальных условий. Но делать этого нет необходимости, поскольку он оформлен в Mathcad в виде встроенных функций.

Рис. 10.2. Иллюстрация метода стрельбы (продолжение листинга 10.1)

Глава 10.2.2. Двухточечные краевые задачи

Решение краевых задач для систем ОДУ методом стрельбы в Mathcad достигается применением двух встроенных функций. Первая предназначена для двухточечных задач с краевыми условиями, заданными на концах интервала:

 sbval(z,x0,x1, D, load, score) — поиск вектора недостающих L начальных условий для двухточечной краевой задачи для системы N ОДУ:

 z — вектор размера Lx1, присваивающий недостающим начальным условиям (на левой границе интервала) начальные значения;  х0 — левая граница расчетного интервала;  xi — правая граница расчетного интервала;  load(x0,z) — векторная функция размера Nx1 левых граничных условий, причем недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента z;  score (x1, у) — векторная функция размера Lx1, выражающая L правых граничных условий для векторной функции у в точке x1;  D(x,y) — векторная функция, описывающая систему N ОДУ, размера Nx1 и двух аргументов — скалярного х и векторного у. При этом у — это неизвестная векторная функция аргумента х того же размера Nx1.

ВНИМАНИЕ!

Решение краевых задач в Mathcad, в отличие от большинства остальных операций, реализовано не совсем очевидным образом. В частности, помните, что число элементов векторов о и load равно количеству уравнений N, а векторов z, score и результата действия функции sbval— количеству правых граничных условий L. Соответственно, левых граничных условий в задаче должно быть (N-L) .

Как видно, функция sbval предназначена не для поиска собственно решения, т. е. неизвестных функций y_i(x), а для определения недостающих начальных условий в первой точке интервала, т. е. y_i(x0). Чтобы вычислить y_i(х) на всем интервале, требуется дополнительно решить задачу Коши. Разберем особенности использования функции sbval на конкретном примере (листинг 10.2), описанном выше (см. разд. 10.1.1). Краевая задача состоит из системы двух уравнений (N=2), одного левого (L=1) и одного правого (N-L=2-1=1) граничного условия.

Листинг 10.2. Решение краевой задачи

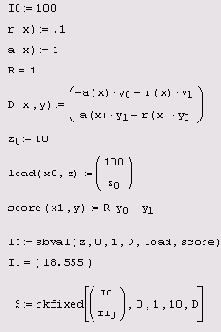
Первые три строки листинга задают необходимые параметры задачи и саму систему ОДУ. В четвертой строке определяется вектор z. Поскольку правое граничное условие всего одно, то недостающее начальное условие тоже одно, соответственно, и вектор z имеет только один элемент z₀. Ему необходимо присвоить начальное значение (мы приняли z₀=10, как в листинге 10.1), чтобы запустить алгоритм стрельбы (см. разд. 10.1.2).

ПРИМЕЧАНИЕ

Начальное значение фактически является параметром численного метода и поэтому может решающим образом повлиять на решение краевой задачи.

В следующей строке листинга векторной функции load(x,z) присваиваются левые граничные условия. Эта функция аналогична векторной переменной, определяющей начальные условия для встроенных функций, решающих задачи Коши. Отличие заключается в записи недостающих условий. Вместо конкретных чисел на соответствующих местах пишутся имена искомых элементов вектора z. В нашем случае вместо второго начального условия стоит аргумент z0 функции load. Первый аргумент функции load — это точка, в которой ставится левое граничное условие. Ее конкретное значение определяется непосредственно в списке аргументов функции sbval. Следующая строка листинга определяет правое граничное условие, для введения которого используется функция score(х,у). Оно записывается точно так же, как система уравнений в функции о. Аргумент х функции score аналогичен функции load и нужен для тех случаев, когда граничное условие явно зависит от координаты х. Вектор score должен состоять из такого же числа элементов, что и вектор z.

Реализованный в функции sbval алгоритм стрельбы ищет недостающие начальные условия таким образом, чтобы решение полученной задачи Коши делало функцию score (х, у) как можно ближе к нулю. Как видно из листинга, результат применения sbval для интервала (0,1) присваивается векторной переменной и. Этот вектор похож на вектор z, только в нем содержатся искомые начальные условия вместо приближенных начальных значений, заданных в z. Вектор и содержит, как и z, всего один элемент и0. С его помощью можно определить решение краевой задачи у (х) (последняя строка листинга). Тем самым функция sbval сводит решение краевых задач к задачам Коши. График решения краевой задачи показан на рис. 10.3.

На рис. 10.4 показано решение той же самой краевой задачи, но с другим правым граничным условием, соответствующим R=0, т. е. без зеркала на правой границе. В этом случае слабый обратный пучок света образуется исключительно за счет обратного рассеяния излучения от лазера. Конечно, многие из читателей уже обратили внимание, что реальная физическая среда не может создавать такого большого рассеяния назад. Иными словами, более реальны значения r(х)<<а (х). Однако когда коэффициенты в системе ОДУ при разных y_i очень сильно (на порядки) различаются, система ОДУ становится жесткой, и функция sbval не может найти решения, выдавая вместо него сообщение об ошибке "Could not find a solution" (Невозможно найти решение).

ВНИМАНИЕ!

Метод стрельбы не годится для решения жестких краевых задач. Поэтому алгоритмы решения жестких ОДУ в Mathcad приходится программировать самому (см. разд. 10.4).

Рис. 10.3. Решение краевой задачи для R=l (продолжение листинга 10.2)

Рис. 10.4. Решение краевой задачи для R=0 (продолжение листинга 10.2 при R=0)

Глава 10.2.3. Краевые задачи с условием во внутренней точке

Иногда дифференциальные уравнения определяются с граничными условиями не только на концах интервала, но и с дополнительным условием в некоторой промежуточной точке расчетного интервала. Чаще всего такие задачи содержат данные о негладких в некоторой внутренней точке интервала решениях. Для них имеется встроенная функция bvaifit, также реализующая алгоритм стрельбы.

 bvaifit(z1,z2,x0,x1,xf,D,load1,load2,score) — поиск вектора недостающих граничных условий для краевой задачи с дополнительным условием в промежуточной точке для системы N ОДУ.

 z1 — вектор, присваивающий недостающим начальным условиям на левой границе интервала начальные значения.  z2 — вектор того же размера, присваивающий недостающим начальным условиям на правой границе интервала начальные значения.  х0 — левая граница расчетного интервала.  x1 — правая граница расчетного интервала.  xf — точка внутри интервала. Dо(х,у) — векторная функция, описывающая систему N ОДУ размера Nx1 и двух аргументов — скалярного х и векторного у. При этом у — это неизвестная векторная функция аргумента х того же размера Nx1.  load1(x0,z) — векторная функция размера Nx1 левых граничных условий, причем недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента z.  load2(x1,z) — векторная функция размера Nx1 левых граничных условий, причем недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента z.  score (xf, у) — векторная функция размера Nx1, выражающая внутреннее условие для векторной функции у в точке xf.

Обычно функция bvaifit применяется для задач, в которых производная решения имеет разрыв во внутренней точке xf. Некоторые из таких задач не удается решить обычным методом пристрелки, поэтому приходится вести пристрелку сразу из обеих граничных точек. В этом случае дополнительное внутреннее условие в точке xf является просто условием сшивки в ней левого и правого решений. Поэтому для данной постановки задачи оно записывается В форме score (xf, у) :=у.

Рассмотрим действие функции bvaifit на знакомом примере модели взаимодействия пучков света (см. рис. 10.1), предположив, что в промежутке между xf=0.5 и x1=1.0 находится другая, оптически более плотная среда с другим коэффициентом ослабления излучения а(х)=3. Соответствующая краевая задача решена в листинге 10.3, причем разрывный показатель ослабления определяется в его второй строке.

Листинг 10.3. Краевая задача с граничным условием в промежуточной точке

Система уравнений и левое краевое условие вводится так же, как и в предыдущем листинге для функции sbval. Обратите внимание, что таким же образом записано и правое краевое условие. Для того чтобы ввести условие отражения на правой границе, пришлось определить еще один неизвестный пристрелочный параметр z20. Строка листинга, в которой определена функция score, задает условие стрельбы — сшивку двух решений в точке xf. В самой последней строке листинга выдан ответ — определенные численным методом значения обоих пристрелочных параметров, которые объединены в вектор а (мы применили в предпоследней строке операцию транспонирования, чтобы результат получился в форме вектора, а не матрицы-строки). Для корректного построения графика решения лучше составить его из двух частей — решения задачи Коши на интервале (x0,xf) и другой задачи Коши для интервала (xf,x1). Реализация этого способа приведена в листинге 10.4, который является продолжением листинга 10.3. В последней строке листинга 10.4 выведено значение второй искомой функции на правой границе интервала. Всегда полезно проконтролировать, что оно совпадает с соответствующим пристрелочным параметром (выведенным в последней строке листинга 10.3).

Листинг 10.4. Решение краевой задачи (продолжение листинга 10.3)

Решение краевой задачи приведено на рис. 10.5. С физической точки зрения естественно, что интенсивность света уменьшается быстрее по мере распространения в более плотной среде в правой половине расчетного интервала. В средней точке xf=0.5, как и ожидалось, производные обоих решений имеют разрыв.

ПРИМЕЧАНИЕ

Еще один пример решения краевых задач с разрывными коэффициентами ОДУ приведен в справочной системе Mathcad.

Рис. 10.5. Решение краевой задачи с разрывом в xf=0.5 (продолжение листингов 10.3—10.4)

Ради справедливости необходимо заметить, что разобранную краевую задачу легко решить и с помощью функции sbval, заменив в листинге 10.2 зависимость а (х) на третью строку листинга 10.3. В этом случае листинг 10.2 даст в точности тот же ответ, что показан на рис. 10.5. Однако в определенных случаях (в том числе из соображений быстроты расчетов) удобнее использовать функцию bvaifit, т. е. вести пристрелку с обеих границ интервала.

СОВЕТ

Если вы имеете дело с подобными уравнениями, попробуйте сначала решить их как обычную краевую задачу с помощью более надежной и легкой в применении функции sbval.

Глава 10.3. Задачи на собственные значения для ОДУ

Задачи на собственные значения — это краевые задачи для системы ОДУ, в которой правые части зависят от одного или нескольких параметров X. Значения этих параметров неизвестны, а решение краевой задачи существует только при определенных λ_k, которые называются собственными значениями (eigenvalues) задачи. Решения, соответствующие этим λ_k, называют собственными функциями (eigenflmctions) задачи. Правильная постановка таких задач требует формулировки количества граничных условий, равного сумме числа уравнений и числа собственных значений. Физическими примерами задач на собственные значения являются, например, уравнение колебаний струны, уравнение Шредингера в квантовой механике, уравнения волн в резонаторах и многие другие.

С вычислительной точки зрения, задачи на собственные значения очень похожи на рассмотренные выше краевые задачи. В частности, для многих из них также применим метод стрельбы (см. разд. 10.1.2). Отличие заключается в пристрелке не только по недостающим левым граничным условиям, но еще и по искомым собственным значениям. В Mathcad для решения задач на собственные значения используются те же функции sbval и bvaifit. В их первый аргумент, т. е. вектор, присваивающий начальные значения недостающим начальным условиям, следует включить и начальное приближение для собственного значения.

Рассмотрим методику решения на конкретном примере определения собственных упругих колебаний струны. Профиль колебаний струны у(х) описывается линейным дифференциальным уравнением второго порядка

где р(х) и q(x) — жесткость и плотность, которые, вообще говоря, могут меняться вдоль струны. Если струна закреплена на обоих концах, то граничные условия задаются в виде у(0)=у(1)=0. Сформулированная задача является частным случаем задачи Штурма—Лиувилля. Поскольку решается система двух ОДУ, содержащая одно собственное значение x, то по идее задача требует задания трех (2+1) условий. Однако, как легко убедиться, уравнение колебаний струны — линейное и однородное, поэтому в любом случае решение у(х) будет определено с точностью до множителя. Это означает, что производную решения можно задать произвольно, например, у' (0)=1, что и будет третьим условием. Тогда краевую задачу можно решать как задачу Коши, а пристрелку вести только по одному параметру — собственному значению.

Процедура поиска первого собственного значения представлена в листинге 10.5.
Листинг 10.5. Решение задачи о собственных колебаниях струны

В первых двух строках листинга определяются функции, входящие в задачу, в том числе р' (х) :=0, и границы расчетного интервала (0,1). В третьей строке дается начальное приближение к собственному значению λ₀, в четвертой вводится система ОДУ. Обратите внимание, что она состоит не из двух, а из трех уравнений. Первые два из них определяют эквивалентную (10.3) систему ОДУ первого порядка, а третье необходимо для задания собственного значения в виде еще одного компонента у₂ искомого вектора у. Поскольку по определению собственное значение постоянно при всех х, то его производная должна быть приравнена нулю, что отражено в последнем уравнении. Важно также, что во втором из уравнений собственное значение записано как у₂, поскольку является одним из неизвестных.

В следующих двух строках листинга задается левое граничное условие, включающее и недостающее условие на собственное значение для третьего уравнения, и правое граничное условие у₀=0. В предпоследней строке листинга обычным образом применяется функция sbval, а в последней выводится результат ее работы вместе с известным аналитически собственным значением п2-я2. Как легко убедиться, мы нашли первое собственное значение для n=1, а чтобы найти другие собственные значения, необходимо задать другие начальные приближения к ним (в третьей строке листинга 10.5). Например, выбор λ₀=50 приводит ко второму собственному значению 2²π², а λ₀=100 — к третьему 3²π2.

Чтобы построить график соответствующей собственной функции, надо добавить в листинг строку, программирующую решение задачи Коши, например, такую: u:=rkfixed(load(a,A) ,а,b, 100,D) . Полученные кривые показаны на рис. 10.6 в виде коллажа трех графиков, рассчитанных для трех собственных значений.

ПРИМЕЧАНИЕ

Примеры решения нескольких задач на собственные значения можно найти в различных Ресурсах Mathcad.

Рис. 10.6. Первые три собственные функции задачи колебаний струны (коллаж трех графиков, рассчитанных листингом 10.5 для разных λ0)

Глава 10.4. Разностные схемы для ОДУ

Многие краевые задачи не поддаются решению методом стрельбы. Однако в Mathcad 12 других встроенных алгоритмов нет. Тем не менее это не означает, что по-другому решать краевые задачи невозможно, ведь другие численные алгоритмы несложно запрограммировать самому пользователю. Рассмотрим возможную реализацию наглядного метода, называемого разностным, которым можно решать краевые задачи как для ОДУ, так и для дифференциальных уравнений в частных производных.

Глава 10.4.1.0 разностном методе

Разберем идею разностного метода решения краевых задач на примере взаимодействия световых пучков (см. рис. 10.1), переобозначив в системе (10.1) интенсивность излучения вправо на Y, а интенсивность излучения влево на у (просто в целях удобства, чтобы не писать в дальнейшем индекс). Суть метода заключается в покрытии расчетного интервала сеткой из N точек. Тем самым определяются (м-l) шагов (рис. 10.7). Затем надо заменить дифференциальные уравнения исходной краевой задачи аппроксимирующими их уравнениями в конечных разностях, выписав соответствующие разностные уравнения для каждого 1-го шага. В нашем случае достаточно просто заменить первые производные из (10.1) их разностными аналогами (такой метод называется еще методом Эйлера):

Рис. 10.7. Сетка, покрывающая расчетный интервал

ПРИМЕЧАНИЕ

Существует множество способов аппроксимации дифференциальных уравнений разностными. От выбора конкретного варианта зависит не только простота, быстрота и удобство вычислений, но и сама возможность получения правильного ответа.

Получилась система (по числу шагов) 2(N-1) разностных линейных алгебраических уравнений с 2N неизвестными Y_i и у_i. Для того чтобы она имела единственное решение, надо дополнить число уравнений до 2N.

Это можно сделать, записав в разностном виде оба граничных условия: \

Y₀=10, Y_N=RY_N. (10.5)

Сформированная полная система алгебраических уравнений называется разностной схемой, аппроксимирующей исходную краевую задачу. Обратите внимание, что правые части разностных уравнений системы (10.4) на каждом шаге записаны для левой границы шага. Такие разностные схемы называют явными, т. к. все значения Y_i+1 и y_i+1 находятся в левой части уравнений. Полученную явную разностную схему легко записать в матричной форме

Аz=В, (10.6)

где z — неизвестный вектор, получающийся объединением векторов Y и у. Решив систему (10.6), мы получим решение краевой задачи.

ПРИМЕЧАНИЕ

На самом деле все несколько сложнее, поскольку, вообще говоря, необходимо еще доказать, что, во-первых, разностная схема действительно аппроксимирует дифференциальные уравнения и, во-вторых, при N->∞ разностное решение действительно сходится к дифференциальному.

Процесс решения системы разностных уравнений называют также реализацией разностной схемы. Программа, которая решает рассматриваемую краевую задачу разностным методом, приведена в листинге 10.6.

Листинг 10.6. Реализация явной разностной схемы

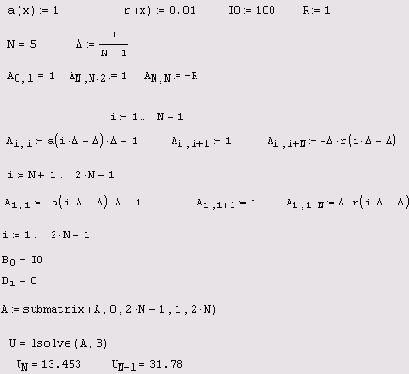
Дадим минимальные комментарии, надеясь, что заинтересовавшийся читатель с карандашом в руках разберется в порядке индексов и соответствии матричных элементов, а возможно, составит и более удачную программу.

В первой строке листинга определяются функции и константы, входящие в модель, во второй задается число точек сетки N=5 и ее равномерный шаг. Следующие две строки определяют матричные коэффициенты, аппроксимирующие уравнения для Y_i; а пятая и шестая — для у_i. Седьмая и восьмая строки листинга задают соответственно левое и правое граничное условие, а строки с девятой по одиннадцатую — правые части системы (10.6). В следующей строке завершается построение матрицы А вырезанием из нее левого нулевого столбца. В предпоследней строке листинга применена встроенная функция isolve для решения системы (10.6), а в последней выведены рассчитанные ею неизвестные граничные значения. Графики решения приведены на рис. 10.8, причем первые N элементов итогового вектора есть вычисленное излучение вперед, а последние N элементов — излучение назад.

Рис. 10.8. Решение краевой задачи разностным методом (продолжение листинга 10.6)

Как мы увидели, реализация в Mathcad разностных схем вполне возможна и не слишком трудоемка — предложенная программа состоит всего из двух десятков математических выражений. Конечно, для их написания требуется и время, и часто кропотливые расчеты, но, собственно, в этом и состоит работа математика. Кстати говоря, при небольшом числе шагов расчеты по разностным схемам не требуют существенного времени (программа, приведенная в листинге 10.6, работает быстрее, чем метод стрельбы, встроенный в функцию sbval). Существуют, кроме того, весьма очевидные для многих читателей пути ускорения расчетов, связанные с применением более подходящих методов решения систем линейных уравнений с разреженной матрицей.

Глава 10.4.2. Жесткие краевые задачи

Один из случаев, когда применение разностных схем может быть очень полезным, связан с решением жестких краевых задач (подробнее о жестких ОДУ читайте в главе 11). В частности, рассматриваемая задача о встречных световых пучках становится жесткой при увеличении коэффициента ослабления а(х) в несколько десятков раз. Например, при попытке решить ее с а(х) :=100 с помощью листинга 10.2 вместо ответа выдается сообщение об ошибке "Can't converge to a solution. Encountered too many integration steps" (He сходится к решению. Слишком много шагов интегрирования). Это и неудивительно, поскольку жесткие системы характерны тем, что требуют исключительно малого значения шага в стандартных алгоритмах.

Для жестких задач неприменимы и явные разностные схемы, о которых рассказывалось в предыдущем разделе (см. разд. 10.3.1). Результат расчетов по программе листинга 10.6, например с а(х) :=20 (рис. 10.9), дает характерную для неустойчивых разностных схем "разболтку" — колебания нарастающей амплитуды, не имеющие ничего общего с реальным решением.

Рис. 10.9. Неверное решение жесткой краевой задачи по неустойчивой явной разностной схеме

Выходом из положения будет использование неявных разностных схем. Применительно к нашей задаче достаточно заменить правые части уравнений (10.1) значениями не на левой, а на правой границе каждого шага:

Граничные условия, конечно, можно оставить в том же виде (10.5). Поскольку мы имеем дело с линейными дифференциальными уравнениями, то и схему (10.7) легко будет записать в виде матричного равенства (10.6), перегруппировывая соответствующим образом выражение (10.7) и приводя подобные слагаемые. Разумеется, полученная матрица А будет иной, нежели матрица А для явной схемы (10.4). Поэтому и решение (реализация неявной схемы) может отличаться от изображенного на рис. 10.9 результата расчетов по явной схеме. Программа, составленная для решения системы (10.7), приведена в листинге 10.7.

Листинг 10.7. Реализация неявной разностной схемы для жесткой краевой задачи

Не будем специально останавливаться на обсуждении листинга 10.7, поскольку он почти в точности повторяет предыдущий листинг. Отличие заключается лишь в формировании матрицы А другим способом, согласно неявной схеме. Решение, показанное на рис. 10.10, демонстрирует, что произошло "небольшое чудо": "разболтка" исчезла, а распределение интенсивностей стало физически предсказуемым. Обратите внимание, что (из-за взятого нами слишком большого коэффициента ослабления излучения) отраженный пучок света имеет очень маленькую интенсивность, и ее пришлось построить на графике с увеличением в тысячу раз.

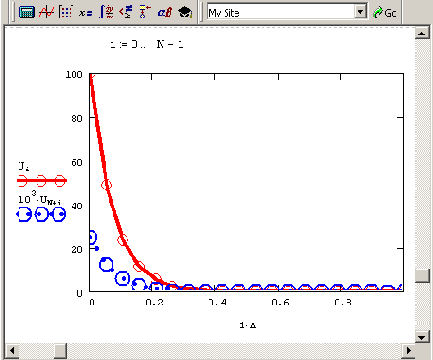
Рис. 10.10. Решение краевой задачи по неявной разностной схеме (продолжение листинга 10.7)

Глава 10.5. Нелинейные краевые задачи

Все примеры, приведенные пока в этом разделе, связаны с краевыми задачами для линейных ОДУ. Между тем на практике часто приходится исследовать именно нелинейные задачи, которые несравненно сложнее с вычислительной точки зрения. Рассмотрим оба подхода к решению нелинейных задач (алгоритм стрельбы и разностный метод), не забывая о том, что нелинейные ОДУ также могут быть в той или иной степени жесткими.

Глава 10.5.1. О постановке задачи

На примере решения нелинейной задачи взаимодействия световых пучков при помощи алгоритма стрельбы разберемся с физикой явления, которую описывает нелинейность. Рассмотрим простейшее усложнение модели (10.1) (см. разд. 10.1), добавив в уравнения малые слагаемые, зависящие квадратично от интенсивности света. Чтобы быть ближе к физической сущности явления, мы введем эту зависимость в формулу коэффициента поглощения среды а(х), сделав а(х) из (10.1) функцией не только координаты, но и суммарной интенсивности:

a(x,Y,y)=a0(x)-ε(x)(Y+y), (10.8)

где а0(х) — постоянная (не зависящая от интенсивности света) составляющая коэффициента поглощения, а е(х) — малый коэффициент пропорциональности. В этом случае модель (10.1) перепишется в виде:

Таким образом, физическая подоплека квадратичной нелинейности задачи (10.9) связана с зависимостью коэффициента поглощения среды от Y+y. Иными словами, чем мощнее свет в некоторой точке среды, тем меньше локальный коэффициент поглощения среды в этой точке.

Механизм этого явления будет хорошо понятен, если предположить, что средой является воздух, насыщенный парами жидкости (попросту говоря, туман). Чем сильнее в некоторой точке туман, тем больше локальное поглощение. Если свет, проходящий через туман, имеет малую интенсивность, то он не оказывает на среду никакого (или почти никакого) воздействия. Однако если пучок света будет очень мощным, за счет его поглощения пары воды будут разогреваться и, следовательно, испаряться. По мере испарения капель воды туман станет рассеиваться, и среда просветлеет (т. е. ее коэффициент поглощения уменьшится). Таким образом, чем мощнее свет, тем активнее пойдет процесс испарения, тем существеннее уменьшится коэффициент поглощения. Именно такой эффект, совершенно понятный с физической точки зрения, и описывает формула (10.8) и, соответственно, модель (10.9).

Подчеркнем еще раз и физический смысл коэффициентов а0(х) и ε(х). Первый описывает постоянный (не зависящий от интенсивности света) коэффициент поглощения среды, а второй — его зависимость от эффекта разогрева среды светом. Чем больше коэффициент а0(х), тем более жесткой является краевая задача; а чем больше ε(х), тем сильнее ее нелинейность. В предельном случае ε(х)->0 задача (10.9) переходит в задачу (10.1), становясь линейной.

Глава 10.5.2. Метод стрельбы

Встроенная функция sbval, реализующая в Mathcad алгоритм стрельбы (см. разд. 10.2), может справляться и с нелинейными задачами. Приведем пример решения краевой задачи (10.9) (листинг 10.8 и рис. 10.11) с теми же граничными условиями, что были поставлены для модели (10.1). Интерес представляет решение у, описывающее рост интенсивности отраженного пучка по мере его распространения справа-налево (обратите внимание, что на рис. 10.11 оно отложено с десятикратным увеличением).
Листинг 10.8. Решение нелинейной краевой задачи методом стрельбы

Следует помнить, что чем сильнее нелинейность и чем жестче краевая задача, тем более сильные требования предъявляются к начальному значению алгоритма, ввод которого осуществляется посредством функции load. Попробуйте повторить расчеты листинга 10.8 с иным сочетанием параметров а0(х) и ε(х), и вы увидите, что с немного более жесткими задачами алгоритм стрельбы уже не справляется.

ПРИМЕЧАНИЕ

На компакт-диске, прилагаемом к книге, вы найдете еще более интересное решение для другой задачи, с нелинейностью типа (y+Y)².

Рис. 10.11. Решение нелинейной краевой задачи (продолжение листинга 10.8)

Глава 10.5.3. Разностные схемы

Решение краевых задач при помощи разностных схем связано с необходимостью разработки собственного алгоритма для каждой конкретной задачи. Как вы помните (см. разд. 10.4), в случае линейных уравнений в результате построения разностной схемы система алгебраических сеточных уравнений также получалась линейной. Это автоматически означало, что она имеет единственное решение, которое в большинстве случаев могло быть найдено стандартными численными методами. В ситуации, когда исходные дифференциальные уравнения нелинейны, система разностных уравнений тоже является нелинейной, и их решение существенно усложняется, хотя бы потому, что оно не является единственным. Поэтому подход к построению разностных схем нелинейных уравнений должен быть специфическим, но наградой за него станет решение задач, с которыми не справляется алгоритм стрельбы (например, жестких).

Подробная разработка алгоритмов и соответствующих программ Mathcad выходит далеко за пределы данной книги, поэтому мы конспективно представим один из приемов решения нелинейных краевых задач, сводящийся к их линеаризации. В общих чертах подход заключается в следующем. Предположим, что некоторое приближение (обозначим его Y(х) и у(х)) к решению нелинейной задачи (10.9) нам известно, и можно считать, что Y->Y+Z и y->y+z, где z и z — близкие к нулю функции х. Тогда, пользуясь их малостью (по сравнению с Y0 и у0), можно разложить нелинейные слагаемые в уравнениях (10.9) в ряд Тейлора по z и z. Получим:

Y'+Z' = -aY + ry + ε(Y² + Yy) - aZ + rz + 2εY(Z + z);     (10.10)

y'+z' = ay - rY - ε(y² + Yy) + az - rz - 2εy(Z + z) .

Теперь, поскольку Y(x) и у(х) являются приближением к решению исходной задачи, то можно считать, что они (приблизительно) удовлетворяют и уравнению, и граничным условиям. Тогда, вычитая (10.9) из (10.10), получим краевую задачу для z (х) и z (х):

Z' = -aZ + rz + 2εY(Z + z);

z' = az - rZ - 2εy(Z + z) ; (10.11)

Z(0) = z(0) = Z(l) = z(l) = 0.

Это и есть та самая новая задача для "маленьких" функций z (х) и z (х), которую надо решить, и которая, благодаря малости z и z, является линейной. Вся беда в том, что мы не знаем "больших" функций Y(x) и у(х), а они, увы, входят в задачу (10.11). Тем не менее рецепт получения этих функций напрашивается сам собой: если нелинейность исходных ОДУ не слишком сильная, то в качестве Y и у можно взять решение линейной краевой задачи, т. е. задачи (10.9) с ε(х)=0 (см. разд. 10.4.1).

Сказанное иллюстрируют листинги 10.9 и 10.10, первый из которых решает линейную краевую задачу (являясь, фактически, небольшой модификацией листинга 10.7 из разд. 10.4.2), а второй решает линеаризованную задачу (10.11), учитывая результат листинга 10.9. В листинге 10.9 матрица о и вектор правых частей в являются разностной аппроксимацией ОДУ (ее первые N строк аппроксимируют первое уравнение, а оставшиеся N строк — второе). Такой же смысл и точно такую же структуру имеют матрица с и вектор правых частей с для второй (линеаризованной) задачи (10.11). Для решения сеточных уравнений Dу=B и Cz=G используется (конечно, весьма неэкономично) встроенная функция isolve, реализующая алгоритм Гаусса.

Важно привлечь внимание читателя к последним строкам листинга 10.9. В них осуществляется интерполяция полученного решения системы сеточных уравнений для того, чтобы в нелинейной задаче (в листинге 10.10) можно было использовать непрерывные "большие" функции из линейной задачи. В последней строке листинга 10.10 осуществляется сложение "больших" и "маленьких" функций (результатов листингов 10.9 и 10.10) для получения полного решения нелинейной задачи (10.9), которое изображено на рис. 10.12.

Не будем давать дополнительных комментариев к Mathcad-программам, надеясь, что читатель, заинтересовавшийся нелинейным примером со световыми пучками и эффектом разогрева светом среды, сам разберется в листингах, тем более что техника разработки разностных схем была нами детально разобрана раньше (см. разд. 10.4).

Листинг 10.9.Решение линейной (приближенной) краевой задачи

Листинг 10.10. Решение линеаризованной задачи (продолжение листинга 10.9)

Последний важный момент, который следует обозначить, связан с решением задач, обладающих значительной нелинейностью. Решение, приведенное в листингах 10.9, 10.10 и на рис. 10.12, согласно самой постановке, должно не сильно отличаться от решения линейной краевой задачи, поскольку функции z(x) и z(x) малы по сравнению с Y(x) и у(х). Если же нелинейность сильная, то решение может сильно отличаться от Y и у, и линеаризация (10.11) будет просто неправильной. В этом случае следует слегка усложнить алгоритм решения нелинейной краевой задачи.

Рис. 10.12. Решение нелинейной краевой задачи разностным методом (продолжение листингов 10.9 и 10.10)

Обозначим полученное в результате решение, как и в листинге 10.10, вектором J(ε), подчеркивая тем самым его зависимость от параметра нелинейности. Очевидно, что J(0) есть решение линейной задачи. Для того чтобы решить задачу с сильной нелинейностью, т. е. довольно большим ε=ε1, можно организовать продолжение по ε как по параметру. Иными словами, используя в качестве начального приближения J (0), можно решить задачу для другого, малого ε=Дε, получив J(Aε), затем, взяв это J(ε) в качестве приближенного решения, получить J(2Aε) и т. д. малыми шагами добраться до желаемого ε1.

ПРИМЕЧАНИЕ

Упрощенную реализацию этого алгоритма вы найдете на компакт-диске, прилагаемом к книге. Она связана с выводом во внешний файл данных результата задачи из листинга 10.10 и считыванием из него же этих данных в качестве входной информации для следующей итерации. В качестве нулевой итерации используется решение линейной задачи, выводимое предварительно в файл из усовершенствованного листинга 10.9.

---

---