Математические задачи в пакете MathCAD 12
Глава 11.1.О постановке задач
Остановимся сначала на общей классификации уравнений в частных производных, принятой в математике, а затем более детально поговорим о постановочной части соответствующих задач на примере различных вариаций уравнения диффузии тепла, которое допускает наглядную физическую интерпретацию.
Глава 11.1.1. Классификация уравнений в частных производных
Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяются спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например, пространственной переменной
х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например,
u(x,t) в некоторой области определения аргументов 0<x<L
и 0<t<T. Граничные условия определяются как заданные временные зависимости функции и, или производных этой функции, на границах расчетной области
0 и L, а начальные — как заданная и (х, 0).
Сами уравнения в частных производных (несколько условно) можно разделить на три основных типа:
параболические — содержащие первую производную по одной переменной и вторую — по другой, причем все эти производные входят в уравнение с одинаковым знаком; гиперболические— содержащие первую производную по одной переменной и вторую — по другой, входящие в уравнение с разными знаками; эллиптические — содержащие только вторые производные, причем одного знака.
Некоторые более сложные уравнения нельзя однозначно подогнать под приведенную классификацию, тогда говорят о гибридных типах уравнений.
Глава 11.1.2. Пример: уравнение диффузии тепла
На протяжении всей главы мы будем использовать в качестве примера очень наглядное и имеющее различные, от очевидных до самых неожиданных, решения уравнение теплопроводности.
Двумерное динамическое уравнение
Рассмотрим следующее параболическое уравнение в частных производных, зависящее от трех переменных — двух пространственных х и у, а также от времени t:

ПРИМЕЧАНИЕ
Выражение в скобках в правой части уравнения (сумму вторых пространственных производных функции и часто, ради краткости, обозначают при помощи оператора Лапласа:
Δu).
Это уравнение называется двумерным уравнением теплопроводности или, по-другому, уравнением диффузии тепла. Оно описывает динамику распределения температуры
u(x,y,t) на плоской поверхности (например, на металлической пластине) в зависимости от времени (рис. 11.1). Физический смысл коэффициента о, который, вообще говоря, может быть функцией как координат, так и самой температуры заключается в задания скорости перетекания тепла от более нагретых областей в менее нагретые. Функция
φ(x,y,t,u) описывает приток тепла извне, т. е. источники тепла, которые также могут зависеть как от пространственных координат (что задает локализацию источников), так и от времени и от температуры и.
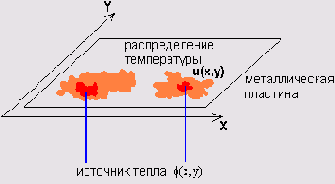
Рис. 11.1. Физическая модель, описываемая двумерным уравнением теплопроводности
Для того чтобы правильно поставить краевую задачу для двумерного уравнения теплопроводности, следует определить следующие дополнительные условия:
граничные условия, т. е. динамику функции u(x,y,t) и (или) ее производных на границах расчетной области; начальное условие, т. е. функцию u(х, у, t).
ПРИМЕЧАНИЕ
Если рассматривается не одно уравнение в частных производных, а система уравнений, то соответствующие начальные и граничные условия должны быть поставлены для каждой из неизвестных функций.
Стационарное двумерное уравнение
Частный случай уравнения теплопроводности определяет стационарную, т. е. не зависящую от времени, задачу. Стационарное уравнение описывает физическую картину распределения температуры по пластине, не изменяющуюся с течением времени. Такая картина может возникнуть при условии, что стационарный источник тепла действует довольно продолжительное время, и переходные процессы, вызванные его включением, прекратились. Пример численного решения такого уравнения показан на рис. 11.2 в виде поверхности
u(х,у).

Рис. 11.2. Решение стационарного двумерного уравнения теплопроводности
(см. листинг 11.7 ниже)
Как несложно сообразить, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и
само уравнение можно переписать (переобозначив ради упрощения
φ<-φ/D) следующим образом:
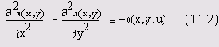
Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Matcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение (11.2), принимающее вид
Δu=0, называют уравнением Лапласа.
Одномерное динамическое уравнение
Предположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (рис. 11.3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:

Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии о=2, нулевым источником ф=о и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на рис. 11.4.
Начиная с версии Mathcad 11, для решения одномерных параболических и гиперболических уравнений можно применять встроенную функцию
pdesolve.
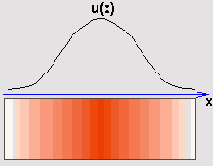
Рис. 11.3. Физическая модель одномерного уравнения теплопроводности

Рис. 11.4. Решение одномерного уравнения теплопроводности (см. листинг 11.1 ниже)
Линейное и нелинейное уравнения
Если присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа.
Линейная задача — если коэффициент диффузии о не зависит от температуры и и, кроме того, если источник тепла ф либо также не зависит от и, либо зависит от и линейно. В этом случае неизвестная функция u (x, t) и все ее производные входят в уравнение только в первой степени (линейно). Нелинейная задача — если уравнение имеет нелинейную зависимость от u(x,t), т. е. или коэффициент диффузии зависит от и, и (или) источник тепла нелинейно зависит от и.
Решения линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми, и их часто можно получить аналитически (этим проблемам посвящены соответствующие разделы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии.
Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически.
ПРИМЕЧАНИЕ
Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями
D(u) и ф(и). В частности, для металлов в большинстве случаев можно считать, что
D=const, в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры.
Обратное уравнение теплопроводности
Замечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с
D=const без источников тепла:

Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает замечательными свойствами.
Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных уравнений (для этого достаточно в листинге 11.1 или 11.2 заменить значение коэффициента диффузии на отрицательное число, например,
D=-1), то мы получим заведомо нефизичное решение. Оно показано на рис. 11.5 в виде профилей распределения температуры для нескольких последовательных моментов времени. Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое решение является не проявлением неустойчивости численного алгоритма (как для ситуации, рассмотренной в разд. "Устойчивость"этой главы), а определяется спецификой самой задачи.
Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того, чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение), приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения.

Рис. 11.5. Численное решение обратного уравнения теплопроводности
дает совершенно нефизичную картину динамики температуры
(см. листинг 11.2 ниже с параметром D=-1)
Глава 11.2. Разностные схемы
Рассмотрим одномерное уравнение теплопроводности (11.3) и на его примере разберем наиболее часто использующийся для численного решения уравнений в частных производных метод сеток. Выпишем еще раз само уравнение
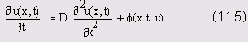
а также и начальное
u(x,0) = u0(x), (11.6)
и граничные условия
u(0, t) = f0(t) , u(L, t) = f1(t), (11.7)
которые необходимы для правильной с математической точки зрения постановки задачи.
Основная идея численного решения уравнений в частных производных очень похожа на метод решения краевых задач для ОДУ, рассмотренный нами в предыдущей главе. Основным отличием от ОДУ является необходимость дискретизации уравнения не по одной, а по нескольким переменным (в зависимости от размерности задачи).
Таким образом, сначала следует покрыть расчетную область (x,t) сеткой и использовать затем узлы этой сетки для разностной аппроксимации уравнения. В результате, вместо поиска непрерывных зависимостей u(x,t) достаточно будет отыскать значения функции в узлах сетки (а ее поведение в промежутках между узлами может быть получено при помощи построения какой-либо интерполяции). По этой причине дискретное представление функции и часто называют сеточной функцией.
Поскольку уравнения в частных производных по определению зависят от производных неизвестных функций по нескольким переменным, то способов дискретизации этих уравнений может быть, как правило, несколько. Конфигурацию узлов, используемую для разностной записи уравнений в частных производных на сетке, называй шаблоном, а полученную систему разностных уравнений — разностной схемой. О принципах построения разностных схем и, в частности, о классах явных и неявных схем мы уже подробно говорили на примере краевых задач для ОДУ (см. разд. 10.4.1), поэтому, излишне не повторяясь, перейдем к рассмотрению типичных особенностей уравнений в частных производных, которые возникают при разработке и реализации разностных схем.
Глава 11.2.1. Явная схема Эйлера
Рассмотрим сначала математические аспекты построения разностной схемы для уравнения диффузии тепла, а затем приведем примеры работы разработанного алгоритма применительно к линейному и нелинейному уравнениям.
Построение разностной схемы
Используем для решения уравнения теплопроводности шаблон, изображенный на рис. 11.6. Для дискретизации второй производной по пространственной координате необходимо использовать три последовательных узла, в то время как для разностной записи первой производной по времени достаточно двух узлов. Записывая на основании данного шаблона дискретное представление для (i, k) -го узла, получим разностное уравнение:
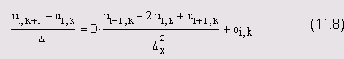
Приведем в разностной схеме (11.8) подобные слагаемые, перенеся в правую часть значения сеточной функции с индексом k (как часто говорят, с предыдущего слоя по времени), а в левую — с индексом k+i
(т. е. со следующего временного слоя). Кроме этого, введем коэффициент с,
который будет характеризовать отношение шагов разностной схемы по времени и пространству

Несколько забегая вперед, заметим, что значение
параметра с, называемого коэффициентом Куранта, имеет большое значение для анализа устойчивости разностной схемы. С учетом этих замечаний, разностная схема (11.8) запишется в виде:
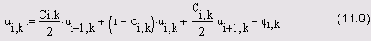

Рис. 11.6. Шаблон аппроксимации явной схемы для уравнения теплопроводности
Множители для каждого из значений сеточной функции в узлах шаблона, соответствующие разностному уравнению (11.9), приведены рядом с каждой точкой шаблона на рис. 11.6. Фактически геометрия шаблона и эти множители задают построенную нами разностную схему.
Несложно убедиться в том, что для получения замкнутой системы разностных алгебраических уравнений систему (11.9) необходимо дополнить дискретным представлением начального и граничных условий (11.6) и (11.7). Тогда число неизвестных будет в точности равно числу уравнений, и процесс формирования разностной схемы будет окончательно завершен.
ПРИМЕЧАНИЕ
Важно подчеркнуть, что возможная нелинейность полученной системы алгебраических уравнений определяется зависимостями от температуры функций
D(u) и ф (u), т. е. как коэффициент диффузии, так и источник тепла могут быть функциями сеточной функции
ui,k.
Если присмотреться к разностным уравнениям (11.9) повнимательнее, то можно сразу предложить несложный алгоритм реализации этой разностной схемы. Действительно, каждое неизвестное значение сеточной функции со следующего временного слоя, т. е. левая часть соотношения (11.9) явно выражается через три ее значения с предыдущего слоя (правая часть), которые
уже известны. Таким образом, в случае уравнения теплопроводности нам очень повезло. Для расчета первого слоя по времени следует попросту подставить в (11.9) начальное условие (известные значения и с нулевого слоя в узлах сетки), для расчета второго слоя достаточно использовать вычисленный таким образом набор и с первого слоя и т. д. Из-за того что разностная схема сводится к такой явной подстановке, ее и называют явной, а благодаря пересчету значений с текущего слоя через ранее вычисленные слои — схемой бегущего счета.
Линейное уравнение
Сделанные замечания относительно реализации явной схемы для уравнения диффузии тепла сразу определяют алгоритм ее программирования в Mathcad. Для решения задачи нужно аккуратно ввести в листинг соответствующие формулы при помощи элементов программирования.
Решение системы разностных уравнений (11.9) для модели без источников тепла, т.е.
ф(x,T,t)=0 и постоянного коэффициента диффузии
D=const приведено в листинге 11.1. В его первых трех строках заданы шаги по временной и пространственной переменным
t и А, а также коэффициент диффузии о, равный единице. В следующих двух строках заданы начальные (нагретый центр области) и граничные (постоянная температура на краях) условия соответственно. Затем приводится возможное программное решение разностной схемы, причем функция пользователя
v(t) задает вектор распределения искомой температуры в каждый момент времени (иными словами, на каждом слое), задаваемый целым числом
t.
Листинг 11.1. Явная схема для линейного уравнения
теплопроводности

Начальное распределение температуры вдоль расчетной области и решение для двух моментов времени показано на рис. 11.7 сплошной, пунктирной и штриховой линиями соответственно. Физически такое поведение вполне естественно — с течением времени тепло из более нагретой области перетекает в менее нагретую, а зона изначально высокой температуры остывает и размывается.

Рис. 11.7. Решение линейного уравнения теплопроводности (продолжение листинга 11.1)
ПРИМЕЧАНИЕ
Несколько забегая вперед, заметим, что показанное на рис. 11.7 решение и соответствует коэффициенту Куранта
С=0.4. Попробуйте осуществить расчет с
увеличенным временным шагом, чтобы коэффициент с был больше 1, и посмотрите, что из этого получится (такой расчет и его объяснение приведены ниже в разд. "Устойчивость").
Нелинейное уравнение
Намного более интересные решения можно получить для нелинейного уравнения теплопроводности, например, с нелинейным источником тепла
ф(u)=103(u-u3). Заметим, что в листинге 11.1 мы предусмотрительно определили коэффициент диффузии и источник тепла в виде пользовательских функций, зависящих от аргумента и, т. е. от температуры. Если бы мы собирались моделировать явную зависимость их от координат, то следовало бы ввести в пользовательскую функцию в качестве аргумента переменную
х, как это сделано для источника тепла ф. Поэтому нет ничего проще замены определения этих функций с констант
D(U)=1 и ф(х,u)=о на новые функции, которые станут описывать другие модели диффузии тепла. Начнем с того, что поменяем четвертую строку листинга 11.1 на ф(х,и)=ю3-(и-и3), не изменяя пока постоянного значения коэффициента диффузии.
ПРИМЕЧАНИЕ
С физической точки зрения, зависимость коэффициента диффузии и функции источника тепла от температуры означает, что эти параметры будут меняться от точки к точке среды, определяясь локальными значениями текущей температуры в этих точках. Ввод ненулевого источника тепла означает, что среда получает определенное количество тепла, тем большее, чем больше локальная температура. Можно догадаться, что введение такой зависимости может моделировать, в частности, горение среды.
Если осуществить расчеты с упомянутым источником (имеющим кубическую нелинейность), то получится очень интересное решение уравнения теплопроводности, имеющее профиль тепловых фронтов. С течением времени граница раздела высокой и низкой температуры распространяется в обе стороны от зоны первичного нагрева, оставаясь весьма четко выделенной (рис. 11.8).
Еще более неожиданные решения возможны при нелинейности также и коэффициента диффузии. Например, если взять квадратичный коэффициент диффузии
D(x,u)=u2 (что с учетом его умножения на неизвестные функции создаст кубическую нелинейность уравнения), а также
ф(х,u)=103-u3-5, то вы сможете наблюдать совсем иной режим горения среды. В отличие от рассмотренного эффекта распространения тепловых фронтов, горение оказывается локализованным в области первичного нагрева среды, причем температура в центре нагрева со временем возрастает до бесконечной величины (рис. 11.9). Такое решение описывает так называемый режим горения "с обострением".
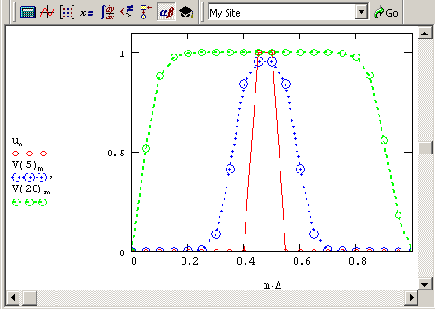
Рис. 11.8. Решение уравнения теплопроводности с нелинейным источником
(тепловой фронт)

Рис. 11.9. Решение уравнения теплопроводности с нелинейным источником и коэффициентом диффузии (режим локализации горения)
Читателю предлагается поэкспериментировать с этим и другими нелинейными вариантами уравнения теплопроводности. Существенно, что такие интересные результаты удается получить лишь численно, а в Mathcad только с применением элементов программирования.
Устойчивость
Как мы убедились, явная разностная схема Эйлера дает вполне разумные результаты и вполне может использоваться для практического моделирования задач, связанных с решением уравнений в частных производных. Однако теперь пришло время сказать об очень важной характеристике разностных схем, которая называется их устойчивостью. Не вдаваясь в детали, заметим, что производить расчеты можно только при помощи устойчивых разностных схем, а чтобы пояснить это понятие, обратимся вновь к листингу 11.1, реализующему явную схему для линейного уравнения диффузии.
Слегка изменим соотношение шагов по времени и пространственной координате, произведя расчеты сначала с
t=0.0005 (эти результаты показаны на рис. 11.7 выше), а также с t=0.0010 и t=0.0015. Результат применения разностной схемы Эйлера для
t=0.0010ю примерно тот же, что и для меньшего значения т, приведенного на рис. 11.7. А вот следующее (казалось бы, незначительное) увеличение шага по времени приводит к катастрофе (рис. 11.10).
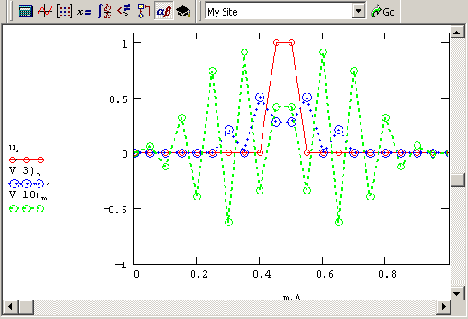
Рис. 11.10. Численное решение уравнения теплопроводности
при помощи явной схемы Эйлера (см. листинг 11.1 ниже с временным шагом t=0.0015)
Вместо ожидаемого решения получаются совершенно неожиданные профили температуры, которые быстро осциллируют вдоль пространственной координаты, причем амплитуда и число пиков этих осцилляции быстро увеличиваются от шага к шагу. Совершенно ясно, что полученное решение не имеет ничего общего с физикой моделируемого явления, а является следствием внутренних свойств самой разностной схемы, которые до этого были для нас скрыты.
Характерная "разболтка" решения как раз и является проявлением неустойчивости явной схемы Эйлера для выбранного соотношения шагов по времени и пространству. В теории численных методов показывается, что явная схема Эйлера для уравнения теплопроводности устойчива при значениях коэффициента Куранта, меньших 1, и неустойчива в противоположном случае. Иными словами, существует ограничение для выбора соотношения шагов, заключающееся в том, что для расчета на более частых пространственных сетках необходимо использовать также и малые шаги по времени.
ПРИМЕЧАНИЕ
Как несложно убедиться, для t=0.0005 коэффициент Куранта C=0.4, для t=0.0010 он все еще меньше единицы:
C=0.8, а для t=0. 0015 решение уже больше единицы: C=1.2, в связи с чем схема становится неустойчивой (см. рис. 11.10).
Глава 11.2.2. Неявная схема Эйлера
В отличие от явной схемы Эйлера, неявная является безусловно-устойчивой (т. е. не выдающей "разболтки" ни при каких значениях коэффициента Куранта). Однако ценой устойчивости является необходимость решения на каждом шаге по времени системы алгебраических уравнений.
Построение неявной разностной схемы
Чтобы построить неявную разностную схему для уравнения диффузии, используем шаблон, изображенный на рис. 11.11, т. е. для дискретизации пространственной производной будем брать значения сеточной функции с верхнего (неизвестного) слоя по времени. Таким образом, разностное уравнение для (i,k)-ro узла будет отличаться от уравнения для явной схемы (11.8) только индексами по временной координате в правой части:

Если привести подобные слагаемые, то получится система уравнений, связывающая
для каждого 1-го узла три неизвестных значения сеточной функции (в самом этом
узле и в соседних с ним слева и справа узлах). Множители при неизвестных значениях сеточной функции в узах шаблона показаны на рис. 11.11 в виде подписей, подобно тому, как это было сделано для явной схемы (см. рис. 11.6).

Рис. 11.11. Шаблон неявной схемы для уравнения теплопроводности
Очень важно, что если само уравнение теплопроводности линейно, то с в левой части разностного уравнения является константой, а
ф в его правой части может зависеть только от первой степени и. Поэтому система уравнений (11.10) для всех пространственных узлов 1=1.. .м-l является линейной системой, что существенно упрощает ее решение (поскольку известно, что для линейных систем с ненулевым определителем решение существует и является единственным). Напомним, что для получения замкнутой системы линейных уравнений необходимо дополнить данный набор разностных уравнений граничными условиями, т. е. известными значениями сеточной функции для i=0 и
i=M.
ПРИМЕЧАНИЕ
Если рассматривать нелинейный случай, то на каждом шаге по времени пришлось бы решать систему нелинейных уравнений, число решений которых могло бы быть большим, и среди них требовалось бы отыскать нужное, а не паразитное решение.
Для реализации неявной схемы, таким образом, можно использовать комбинацию
средств программирования Mathcad и встроенной функции решения системы линейных
уравнений isolve. Один из возможных способов решения предложен в листинге 11.2.
Большая часть этого листинга является вводом параметров задачи (шагов, начальных
и граничных условий), и только в последней его строке определяется функция
пользователя, вычисляющая сеточную функцию на каждом временном слое (при помощи
встроенной функции решения системы линейных уравнений isolve). В нескольких
предыдущих строках листинга (после расчета коэффициента Куранта сои) формируется
матрица системы уравнений А, которая записывается в подходящем для Mathcad виде, как это сделано в листинге 11.2. Как несложно убедиться, столбец правых частей разностных уравнений выражается вычисленными значениями сеточной функции с предыдущего слоя.
Результаты расчетов по неявной схеме показаны на рис. 11.12 и, как видно, они дают примерно те же результаты, что и в случае применения явной схемы (см. рис. 11.7). Обратите внимание, что решение устойчиво при любых значениях коэффициента Куранта (в том числе и больших 1), поскольку, как следует из соответствующих положений теории численных методов, неявная схема является безусловно-устойчивой.

Рис. 11.12. Решение линейного уравнения теплопроводности при помощи неявной схемы на первом слое по времени (листинг 11.2)
Листинг 11.2. Неявная схема для линейного уравнения теплопроводности

Алгоритм прогонки
Приведем в данном разделе описание чрезвычайно популярного алгоритма реализации неявных разностных схем, который называется методом прогонки. Этот алгоритм имел историческое значение для становления технологий расчетов уравнений в частных производных, и мы просто не можем не упомянуть о нем в этой книге.
ПРИМЕЧАНИЕ
Сразу оговоримся, что его применение для решения уравнений в частных производных в среде Mathcad может быть оправдано, только если вы работаете с очень частыми сетками, которые приводят к системам разностных уравнений большой размерности и, соответственно, очень большому времени вычислений.
Основным вычислительным ядром программы, реализующей на Mathcad неявную разностную схему, было решение (на каждом временном слое) системы линейных алгебраических уравнений, задаваемых матрицей А. Заметим, что эта матрица, как говорят, имеет диагональное преобладание, а точнее, является трехдиагоналъной (рис. 11.13). Все ее элементы, кроме элементов на главной диагонали и двух соседних диагоналях, равны нулю. С точки зрения оптимизации быстродействия алгоритма применение встроенной функции
isolve является весьма расточительным, поскольку основной объем арифметических операций, выполняемых компьютером (а он составляет, как нетрудно убедиться, величину порядка м2), сводится к непроизводительному перемножению нулей.
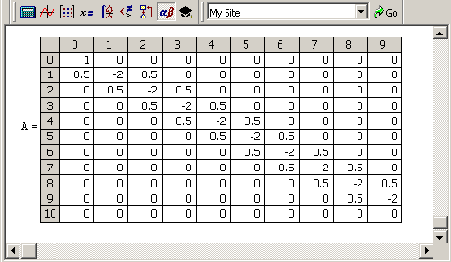
Рис. 11.13. Матрица системы линейных разностных уравнений для неявной схемы (листинг 11.2 для
M=10)
Для отыскания решения линейных систем алгебраических уравнений имеется чрезвычайно эффективный алгоритм, называемый прогонкой, который позволяет уменьшить число арифметических операций на целый порядок, т. е. до значения порядка м. Это означает, что при использовании пространственных сеток с юоо узлами выигрыш во времени вычислений составит величину порядка ю3! Реализация данного алгоритма приведена в листинге 11.3, который является продолжением листинга 11.2, используя определенные в нем коэффициенты матрицы
А, а также начальное условие.
Программа листинга 11.3 осуществляет пересчет одного шага по времени, т. е. заменяет содержимое столбца и с предыдущего временного слоя вычисленными значениями неизвестной функции со следующего слоя. Первые пять строк листинга 11.3 представляют так называемый обратный ход прогонки, а последние две строки — ее прямой ход. Заинтересовавшемуся читателю предлагается самому оформить представленный алгоритм прогонки в виде программы решения разностных уравнений для вычисления произвольного временного слоя по примеру листингов 11.1 и 11.2. Заметим, что описание этого знаменитого алгоритма можно отыскать практически в любом современном учебнике по численным методам.
Листинг 11.3. Алгоритм прогонки (продолжение
листинга 11.2)
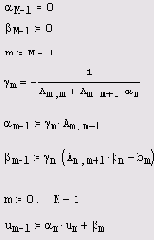
Глава 11.2.3.О возможности решения многомерных уравнений
Все, что было сказано до сих пор, касалось исключительно способов решения одномерных (в смысле пространственных координат) уравнений. И алгоритмы разностных схем, и встроенные функции, включая появившиеся в 11-й версии (см. следующий разд.), относились к уравнениям, зависящим от одной пространственной координаты.
Можно ли при помощи Mathcad решать двумерные или трехмерные (пространственные) уравнения? С точки зрения программирования пользователем численных алгоритмов типа метода сеток принципиальных ограничений нет. Разумеется, если сначала аккуратно выписать разностную схему соответствующего многомерного дифференциального уравнения, то вполне возможно запрограммировать ее при помощи описанных нами средств. Самым главным противодействием будет существенное увеличение времени расчетов. Простая оценка необходимого количества операций показывает, что если ввод зависимости уравнения от второй пространственной координаты многократно увеличивает число разностных уравнений, которые должны решаться при реализации каждого шага по времени. К примеру, если используется пространственная сетка из 100 узлов по каждой координате, то вместо 102 разностных уравнений на каждом шаге придется решать уже 104 уравнений, т. е. объем вычислений сразу же возрастает в 100 раз. Вообще говоря, пакет Mathcad не является экономичной средой вычислений, и бороться с их сильно возрастающим объемом следует пользователю еще на этапе разработки алгоритма. Хорошим примером такой борьбы может служить применение специфических алгоритмов, типа метода прогонки (см. разд. "Алгоритм прогонки"этой главы).
Приведем некоторые дополнительные замечания, связанные с возможностью осуществить редукцию громоздких (в смысле организации вычислений) двумерных задач к более простым. Рассмотрим ради примера двумерное уравнение теплопроводности (11.1) без источника с нулевыми граничными
условиями и некоторым начальным двумерным распределением температуры по расчетной поверхности:

Произведем дискретизацию данного уравнения по временной координате, заменяя первую производную ее разностным аналогом и несколько перегруппировывая слагаемые и множители:
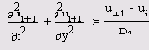
Как вы видите, мы используем неявную разностную схему, заранее заботясь о том, чтобы разностная задача была более устойчивой. Здесь
ui(x,y) — известная с предыдущего шага по времени функция двух пространственных переменных, а и1+1(х,у) — функция, подлежащая определению при реализации каждого шага по времени.
Посмотрим на полученную задачу с несколько другой стороны — а именно как на дифференциальное уравнение относительно неизвестной функции двух переменных
ui+1(x,y). Подчеркнем, что такое уравнение получается для каждого шага по времени, т. е. для реализации всей разностной схемы требуется решить большое число таких уравнений.
С предложенной точки зрения, на каждом временном шаге необходимо решить некоторое двумерное эллиптическое линейное уравнение, причем его граничные условия определяются граничными условиями исходной задачи. Это уравнение очень похоже на уравнение Пуассона с той лишь разницей, что в его правую часть, описывающую источник, входит неизвестная функция (к счастью, линейно). Таким образом, зависимость от найденного на предыдущем шаге по времени решения определяется зависимостью от него источника, т. е. правой части.
Суммируя сказанное, можно констатировать, что если вы имеете запрограммированный алгоритм решения выписанного эллиптического уравнения, чуть более сложного, чем уравнение Пуассона, то его с легкостью можно использовать в качестве подпрограммы реализации разностной схемы двумерного уравнения теплопроводности. Забегая вперед, приходится отметить, что, к сожалению, встроенные функции Mathcad для решения уравнения Пуассона в данном случае не годятся в качестве такой подпрограммы, поскольку предполагают независимость источника от самой неизвестной функции, и могут справляться лишь с правой частью, зависящей только от пространственных координат (см. разд. 11.3.2).
Не будем далее останавливаться на способах решения многомерных уравнений, ограничившись этими замечаниями относительно путей оптимизации алгоритмов их решения.
Глава 11.3. Встроенные функции для решения уравнений в частных производных
Как видно из предыдущего раздела, с уравнениями в частных производных вполне можно справиться и не прибегая к специфическим средствам Mathcad. Между тем в версиях Mathcad
11 (и выше) имеется несколько встроенных функций, при помощи которых можно автоматизировать процесс решения дифференциальных уравнений в частных производных. Рассмотрим в данном разделе основные аспекты их применения, отмечая не только инструкции по их применению, описанные разработчиками Mathcad, но также и некоторые "скрытые" возможности этих функций.
Глава 11.3.1. Параболические и гиперболические уравнения
Разработчики впервые применили дополнительные встроенные функции для решения параболических и гиперболических уравнений в частных производных в версии Mathcad 11, отлично осознавая значимость этих задач для современного исследователя и инженера. Предусмотрены два варианта решения: при помощи вычислительного блока
Given/pdesolve, а также при помощи встроенной функции
numol. Первый путь проще в применении и нагляднее, зато второй позволяет автоматизировать процесс решения уравнений в частных производных, например, если нужно включить его в качестве составного шага в более сложную Mathcad-программу.
Вычислительный блок Given /pdesolve
Встроенная функция pdesolve применяется в рамках вычислительного блока, начинающегося ключевым словом
Given, и пригодна для решения различных гиперболических и параболических уравнений. Она предназначена для решения одномерного уравнения (или системы уравнений) в частных производных (того, которое определит пользователь в рамках вычислительного блока
Given), зависящего от времени t и пространственной координаты х, имеет целый набор различных аргументов и работает следующим образом:
pdesolve(u,x,xrange,t,trange,[xpts],[tpts])) — Возвращает скалярную (для единственного исходного уравнения) или векторную (для системы уравнений) функцию двух аргументов (x,t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных. Результирующая функция получается интерполяцией сеточной функции, вычисляемой согласно разностной схеме:
u — явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия (в форме Дирихле или Неймана) должны быть определены пользователем перед применением функции pdesolve в вычислительном блоке после ключевого слова Given. Если решается не система уравнений в частных производных, а единственное уравнение, то, соответственно, вектор и должен содержать только одно имя функции и вырождается в скаляр; х — пространственная координата (имя аргумента неизвестной функции); xrange — пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала); t — время (имя аргумента неизвестной функции); t range — расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени); xpts — количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически); tpts — количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно).
В качестве примера использования функции pdesolve (листинг 11.4) используем то же самое одномерное уравнение теплопроводности (11.5) с граничными и начальными условиями (11.6) и (11.7).
Листинг 11.4. Решение одномерного уравнения теплопроводности

Для корректного использования функции pdesolve предварительно, после ключевого слова
Given, следует записать само уравнение и граничные условия при помощи логических операторов (для их ввода в Mathcad существует специальная панель). Обратите внимание, что уравнение должно содержать имя неизвестной функции u(x,t) вместе с именами аргументов (а не так, как она записывается в пределах встроенной функции
pdesolve). Для идентификации частных производных в пределах вычислительного блока следует использовать нижние индексы, например,
uxx(,t), для обозначения второй производной функции и по пространственной координате
х.
Как видно из рис. 11.14, на котором изображены результаты расчетов по листингу 11.4, встроенная функция с успехом справляется с уравнением диффузии, отыскивая уже хорошо знакомое нам решение. Заметим, что использование встроенной функции
pdesolve связано с довольно громоздкими вычислениями, которые могут отнимать существенное время.
ПРИМЕЧАНИЕ
Как вы можете заметить, выбирать величину шага по пространственной и временной переменным может как сам алгоритм, так и пользователь (неявным образом, через число узлов сетки). Читателю предлагается повторить вычисления листинга 11.4 для различных комбинаций параметров (главным образом, числа узлов сетки), чтобы проверить, в каких случаях алгоритм встроенной функции справляется с задачей, выдавая верное решение, а в каких дает сбой.

Рис. 11.14. Решение уравнения диффузии тепла при помощи встроенной функции pdesoдve (листинг 11.4)
Пример: волновое уравнение
Приведем еще один пример применения функции pdesoive для решения уравнений в частных производных. Рассмотрим одномерное волновое уравнение, которое описывает, например, свободные колебания струны музыкального инструмента:
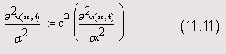
Здесь неизвестная функция u(x,t) описывает динамику смещения профиля струны относительно невозмущенного (прямолинейного) положения, а параметр с характеризует материал, из которого изготовлена струна.
Как вы видите, уравнение (11.11) содержит производные второго порядка, как по пространственной координате, так и по времени. Для того чтобы можно было использовать встроенную функцию
pdesolve, необходимо переписать волновое уравнение в виде системы двух уравнений в частных производных, введя вторую неизвестную функцию
v=ut. Программа для решения волнового уравнения приведена в листинге 11.5, а результат— на рис. 11.15.
Листинг 11.5. Решение волнового уравнения

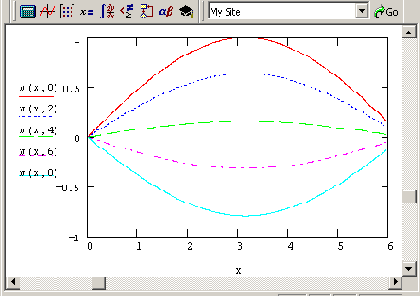
Рис. 11.15. Решение волнового уравнения (продолжение листинга 11.5)
Встроенная функция numol
Альтернативный вариант решения дифференциальных уравнений в частных производных заключается в применении еще одной встроенной функции
numo|, которая реализует тот же самый алгоритм сеток, позволяя вручную задать большинство его параметров:
numol(xrange,xpts,trange,tpts,Npde,Nae,rhs,init,bc) — Возвращает матрицу решения дифференциального уравнения в частных производных, представляющую искомую сеточную функцию в каждой точке по пространственной (по строкам) и временной координате (по столбцам). Если решается не одно уравнение, а система уравнений, то результатом является составная матрица, образованная путем слияния (слева-направо) матриц со значениями каждой искомой сеточной функции:
Npde — общее количество дифференциальных уравнений в частных производных в системе; Nae — общее количество дополнительных алгебраических уравнений, которые также могут входить в систему; rhs — векторная функция, определяющая систему дифференциальных и алгебраических уравнений (формат этого и двух следующих матричных параметров объяснен в листинге 11.9); init — векторная функция, определяющая начальные условия для каждой неизвестной функции; be — функциональная матрица граничных условий; xrange — пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала); xpts — количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически); trange — расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени); tpts — количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно);
Пример решения волнового уравнения при помощи функции numol приведен в листинге 11.6, особое внимание в котором мы призываем уделить формату представления векторов rhs, init и be, а также принципу извлечения отдельных сеточных решений из матрицы-результата. График решения, показанный на рис. 11.16, полезно сравнить с результатом применения вычислительного блока из предыдущего раздела (см. листинг 11.5 и рис. 11.15).
Листинг 11.6. Решение волнового уравнения при помощи функции numol

Как вы видите, функция numol имеет еще большее число аргументов, нежели
pdesolve, и позволяет автоматизировать применение метода сеток. Однако пользоваться ею намного сложнее, чем вычислительным блоком, поскольку и уравнения, и начальные и граничные условия должны быть записаны в специальном формате. Применение функции
numol оправданно, когда необходимо включить решение уравнений в частных производных в более сложные вычисления в качестве подпрограммы, организовать серию расчетов с меняющимся параметром, подготовить анимацию графиков решения и т. п.

Рис. 11.16. Решение волнового уравнения (продолжение листинга 11.6)
Именно в целях визуализации решения параболических и гиперболических уравнений в частных производных использование функции
numol наиболее полезно. График решения динамических уравнений (зависящих от времени t) выглядит намного эффектнее и воспринимается несравненно лучше, если он оформлен в виде анимации. Для создания анимационных роликов расчетное время следует выразить через константу
FRAME и затем применить команду View / Animate (Вид / Анимация) (см. разд. 13.3.2).
Глава 11.3.2. Эллиптические уравнения
Решение эллиптических уравнений в частных производных реализовано только для единственного типа задач — двумерного уравнения Пуассона.
Это уравнение содержит вторые производные функции u(х,у) по двум пространственным переменным;
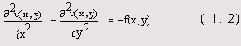
Уравнение Пуассона описывает, например, распределение электростатического поля
u(х,у) в двумерной области с плотностью заряда f (x,y), или (см. разд. 11.1.2) стационарное распределение температуры
u(х,у) на плоскости, в которой имеются источники (или поглотители) тепла с интенсивностью
f (х,у) .
ПРИМЕЧАНИЕ
Несмотря на то, что применение встроенных функций, описанных в данном разделе, анонсировано разработчиками Mathcad только для уравнения Пуассона, их можно применять и для решения других уравнений, даже необязательно эллиптического типа. О том, как осуществить такие расчеты, написано в конце данного раздела.
Уравнение Пуассона
с нулевыми граничными условиями
Корректная постановка краевой задачи для уравнения Пуассона требует задания граничных условий. В Mathcad решение ищется на плоской квадратной области, состоящей из
(M+1)х(M+1) точек. Поэтому граничные условия должны быть определены пользователем для всех четырех сторон упомянутого квадрата. Самый простой вариант — это нулевые граничные условия, т. е. постоянная температура по всему периметру расчетной области. В таком случае можно использовать встроенную функцию
multigrid:
multigrid(F,ncycie) — матрица решения уравнения Пуассона размера (м+1)х(м+1) на квадратной области с нулевыми граничными условиями:
F — матрица размера (M+1)х(M+1), задающая правую часть уравнения Пуассона; ncycle — параметр численного алгоритма (количество циклов в пределах каждой итерации).
ВНИМАНИЕ!
Сторона квадрата расчетной области должна включать точно N=2n шагов, т. е. 2n+1 узлов, где
n — целое число.
Параметр численного метода ncycle в большинстве случаев достаточно взять равным 2. Листинг 11.7 содержит пример использования функции
multigrid для расчета краевой задачи на области 33х33 точки и точечным источником тепла в месте, задаваемом координатами (15,20) внутри этой области.
Листинг 11.7.Решение уравнения Пуассона с нулевыми
граничными условиями

В первой строке листинга задается значение м=32, в двух следующих строках создается матрица правой части уравнения Пуассона, состоящая из всех нулевых элементов, за исключением одного, задающего расположение источника. В последней строке матрице с присваивается результат действия функции
multigrid. Обратите внимание, первый ее аргумент сопровождается знаком "минус", что соответствует записи правой части уравнения Пуассона (11.11). Графики решения показаны на рис. 11.17 и 11.18 в виде трехмерной поверхности и линий уровня соответственно.

Рис. 11.17. График поверхности решения уравнения Пуассона (продолжение листинга 11.7)

Рис. 11.18. График линий уровня решения уравнения Пуассона (продолжение листинга 11.7)
Уравнение Пуассона с произвольными граничными условиями
В более сложных случаях, например, для решения краевой задачи с ненулевыми условиями на границах, следует использовать другую встроенную функцию
relax, имеющуюся в Mathcad:
relax(a,b,c,d,e,F,v,rjac) — матрица решения дифференциального уравнения в частных производных на квадратной области, полученного с помощью алгоритма релаксации для метода сеток:
a,b,c,d,e — квадратные матрицы коэффициентов разностной схемы, аппроксимирующей дифференциальное уравнение; F — квадратная матрица, задающая правую часть дифференциального уравнения; v — квадратная матрица граничных условий и начального приближения к решению; rjac — параметр численного алгоритма (спектральный радиус итераций Якоби);
Параметр численного алгоритма характеризует скорость сходимости итераций. Он должен быть числом от о до 1. В матрице граничных условий v необходимо задать только граничные элементы, исходя из значения краевых условий по периметру расчетной области. Прочие (внутренние) элементы этой матрицы служат для задания начального приближения к решению.
Суть алгоритма релаксации сводится к тому, что в ходе итераций происходит проверка уравнений и соответствующая коррекция значений искомой функции в каждой точке. Если начальное приближение выбрано удачно, то можно надеяться, что алгоритм сойдется ("релаксирует") к правильному решению.
ВНИМАНИЕ!
Все матрицы, задающие как коэффициенты разностной схемы а, b, с, d, e, граничные условия
v, так и само решение F, должны иметь одинаковый размер (M+1)х(M+1), соответствующий размеру расчетной области. При этом целое число м обязательно должно быть степенью двойки: м=2п.
Решение уравнения Пуассона с тремя источниками разной интенсивности при помощи функции
relax приведено в листинге 11.8.
Листинг 11.8. Решение уравнения Пуассона с помощью функции relax
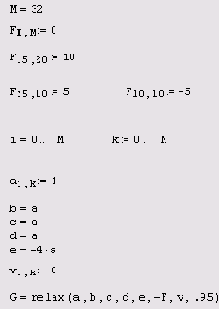
Первые три строки имеют тот же смысл, что и в предыдущем листинге. Только вместо одного источника тепла взято их другое распределение — один сильный источник, один более слабый и один сток тепла. В следующих шести строках задаются коэффициенты разностной схемы. Отложим их обсуждение до последнего раздела этой главы, ограничившись утверждением, что для решения уравнения Пуассона коэффициенты должны быть взяты именно такими, как показано в листинге 11.8. В предпоследней строке задана матрица нулевых граничных условий и нулевых начальных приближений, а в последней матрице с присваивается результат действия функции
relax. График полученного решения в виде линий уровня показан на рис. 11.19.

Рис. 11.19. Решение уравнения Пуассона с помощью функции relax (продолжение листинга 11.8)
Разностная схема для решения уравнения Пуассона
Несмотря на отсутствие сведений в справочной системе Mathcad о решении других линейных дифференциальных уравнений в частных производных, кроме уравнения Пуассона, сделать это возможно с помощью той же функции
relax (см. предыдущий разд.). Для этого нужно правильным образом задать коэффициенты разностной схемы.
Начнем с пояснения выбора этих коэффициентов (см. листинг 11.8) для уравнения Пуассона. Согласно основным идеям метода сеток (см. разд. 11.2), для дискретизации обеих пространственных производных в уравнении (11.12) следует использовать по три соседних узла вдоль каждой из координат. Поэтому уравнение Пуассона (11.12) может быть
записано в разностной форме при помощи шаблона типа "крест" (рис. 11.20). В этом случае, после приведения подобных слагаемых в разностных уравнениях коэффициенты разностной схемы будут такими, как показано возле узлов шаблона на этом рисунке (аналогичные коэффициенты для явной и неявных схем решения уравнения теплопроводности см. на рис. 11.6 и 11.11 соответственно).
Теперь, если вы сравните полученные числа с константами, которые присвоены элементам матриц-аргументов функции
relax (см. листинг 11.8), то увидите, что они как раз и описывают вычисленные нами только что коэффициенты разностной схемы "крест". Таким образом, нетрудно сообразить, что с помощью встроенной функции
relax можно решать и другие линейные дифференциальные уравнения в частных производных, которые можно аппроксимировать схемой типа "крест" или схемой, являющейся ее составной частью. Конечно, для того чтобы использовать эту встроенную функцию для другого уравнения, необходимо будет составить соответствующую разностную схему.

Рис. 11.20. Шаблон аппроксимации уравнения Пуассона "крест"
Решение уравнения диффузии тепла при помощи функции relax
Приведем пример применения встроенной функции relax для решения другого уравнения в частных производных (т. е. не уравнения Пуассона, для которого она изначально предназначена). Вычислим при помощи этой функции решение уже хорошо нам знакомого однородного линейного уравнения теплопроводности (см. разд. 11.1.2). Будем использовать явную разностную схему, шаблон которой изображен на рис. 11.6. Для того чтобы "приспособить" для явной схемы функцию
relax, требуется только задать ее аргументы в соответствии с коэффициентами, показанными на шаблоне (см. рис. 11.6). Программа, реализующая таким способом явную схему, представлена на листинге 11.9. Число Куранта в этом листинге обозначено переменной с, как и положено явной разностной схеме, она выдает устойчивое решение только для
C<1.
Листинг 11.9. Решение уравнения теплопроводности при помощи функции
relax
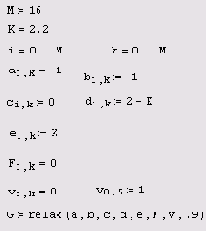
Результат действия программы листинга 11.9 показан на рис. 11.21 в виде трехмерной поверхности. Если сравнить рис. 11.21 с рис. 11.4, полученным при расчетах по запрограммированной разностной схеме, то в графиках рис. 11.4 нетрудно узнать сечения этой поверхности плоскостями
t=const. Еще раз подчеркнем, что использовать встроенную функцию можно только для тех уравнений, которые допускают построение разностной схемы типа "крест" (см. рис. 11.17) или составного фрагмента этой схемы.

Рис. 11.21. Решение уравнения теплопроводности с помощью функции relax (продолжение листинга 11.9)