Математические задачи в пакете MathCAD 12
Глава 13.1. Интерполяция
Для построения интерполяции-экстраполяции в Mathcad имеется несколько встроенных функций, позволяющих "соединить" точки выборки данных
(xi,yi) кривой разной степени гладкости. По определению интерполяция означает построение функции А(Х), аппроксимирующей зависимость у(х) в промежуточных точках (между
xi). Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках xi
значения интерполяционной функции должны совпадать с исходными данными, т. е. A(xi)=y (xi).
ПРИМЕЧАНИЕ
Везде в этом разделе, при рассказе о различных типах интерполяции будем использовать вместо обозначения А(х) другое имя ее аргумента
A(t), чтобы не путать вектор данных х и скалярную переменную t.
Глава 13.1.1. Линейная интерполяция
Самый простой вид интерполяции — линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(х) состоит из отрезков прямых, соединяющих точки (рис. 13.2).

Рис. 13.2. Линейная интерполяция (продолжение листинга 13.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 13.1):
linterp(х,у,t) — функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью:
х — вектор действительных данных аргумента; у — вектор действительных данных значений того же размера; t — значение аргумента, при котором вычисляется интерполирующая функция.
ВНИМАНИЕ!
Элементы вектора х должны быть определены в порядке возрастания, т. е.
Xl<X2<X3<. . .<XN.
Листинг 13.1. Линейная интерполяция

Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
1. Ввести векторы данных х и у (первые две строки листинга).
2. Определить функцию linterp (х, у, t).
3. Вычислить значения этой функции в требуемых точках, например,
linterp(х,у,2.4)=3.52, или linterp(х,у,6)=5.9, или постройте ее График, как показано на рис. 13.2.
ПРИМЕЧАНИЕ
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция
A(t) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале
(0,6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции
А(х) от векторного аргумента х (рис. 13.3) Mathcad по умолчанию соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).

Рис. 13.3. Обычное построение графика функции от векторной переменной х (продолжение листинга 13.1)
Глава 13.1.2. Кубическая сплайн-интерполяция
В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т. е. отрезками кубических парабол (рис. 13.4):
interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у кубическими сплайнами:
s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline; х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; у — вектор действительных данных значений того же размера; t — значение аргумента, при котором вычисляется интерполирующая функция.
Сплайн-интерполяция в Mathcad реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определить первый из ее аргументов — векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х, у):
ispline (х, у) — вектор значений коэффициентов линейного сплайна; pspiine(x,y) — вектор значений коэффициентов квадратичного сплайна; cspline (х, у) — вектор значений коэффициентов кубического сплайна:
х, у — векторы данных.
Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяции приведен в листинге 13.2.
Листинг 13.2. Кубическая сплайн-интерполяция

Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости
A(t)=at3+bt2+ ct+d. Коэффициенты
а, b, с, d рассчитываются независимо для каждого промежутка, исходя из значений
у* в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения
A(t) в любой точке t (рис. 13.4).

Рис. 13.4. Сплайн-интерполяция (продолжение листинга 13.2)
Чтобы подчеркнуть различия, соответствующие разным вспомогательным функциям cspline,
pspline, ispline, покажем результат действия листинга 13.2 при замене функции
cspline в предпоследней строке на линейную ispline (рис. 13.5). Как видно, выбор вспомогательных функций существенно влияет на поведение
A(t) вблизи граничных точек рассматриваемого интервала (0,6) и особенно разительно меняет результат экстраполяции данных за его пределами.
В заключение остановимся на уже упоминавшейся в предыдущем разделе распространенной ошибке при построении графиков интерполирующей функции (см. рис. 13.3). Если на графике, например, являющемся продолжением листинга 13.2, задать построение функции А<Х) вместо A(t), то будет получено просто соединение исходных точек ломаной (рис. 13.6). Так происходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.

Рис. 13.5. Сплайн-интерполяция с выбором коэффициентов линейного сплайна
lspline

Рис. 13.6. Ошибочное построение графика сплайн-интерполяции (продолжение листинга 13.2)
Глава 13.1.3. Полиномиальная сплайн-интерполяция
Более сложный тип интерполяции — так называемая интерполяция В-сплайнами. В отличие от обычной сплайн-интерполяции (см. разд. 13.1.2), сшивка элементарных В-сплайнов производится не в точках
хi а в других точках
ui, координаты которых предлагается ввести пользователю. Сплайны могут быть полиномами 1, 2 или
3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна.
interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у с помощью В-сплайнов. bspiine (x,y,u,n) — вектор значений коэффициентов В-сплайна:
s — вектор вторых производных, созданный функцией bspline; х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; у — вектор действительных данных значений того же размера; t — значение аргумента, при котором вычисляется интерполирующая функция; u — вектор значений аргумента, в которых производится сшивка В-сплайнов; n — порядок полиномов онлайновой интерполяции (1, 2 или з).
ПРИМЕЧАНИЕ
Размерность вектора и должна быть на 1, 2 или 3 меньше размерности векторов
х и у. Первый элемент вектора и должен быть меньше или равен первому элементу вектора
х, а последний элемент и — больше или равен последнему элементу х.
Интерполяция В-сплайнами иллюстрируется листингом 13.3 и рис. 13.7.
Листинг 13.3. Интерполяция В-сплайнами


Рис. 13.7. В-сплайн-интерполяция (продолжение листинга 13.3)
Глава 13.1.4. Сплайн-экстраполяция
Все описанные в предыдущих разделах типы интерполяции работают также и как функции экстраполяции данных. Для вычисления экстраполяции достаточно просто указать соответствующее значение аргумента, которое лежит за границами рассматриваемого интервала. С этой точки зрения разницы в применении в Mathcad между интерполяцией и экстраполяцией нет.
На практике при построении экстраполяции следует соблюдать известную осторожность, не забывая о том, что ее успех определяется значимостью ближайших к границе интервала точек. Чем дальше от них вы будете пытаться экстраполировать зависимость, заданную экспериментальными точками, тем сомнительнее будет результат. Сказанное иллюстрируется рис. 13.8 и 13.9, на которых изображена линейная (пунктир на обоих графиках) и сплайн- (сплошные кривые) экстраполяция. На рис. 13.8 используется линейная сплайн-экстраполяция при помощи функции
ispline (см. рис. 13.5 в качестве примера интерполяции), а на рис. 13.9 — функции кубического сплайна
cspline (что соответствует листингу 13.2 и рис. 13.4). Видно, что вдали от рассматриваемого интервала результаты экстраполяции совершенно различны, что, конечно, объясняется тем, что она является ни чем иным как параболической зависимостью.

Рис. 13.8. Линейная сплайн-экстраполяция

Рис. 13.9. Квадратичная сплайн-экстраполяция (продолжение листинга 13.2)
Глава 13.1.5. Экстраполяция функцией предсказания
Как мы увидели (см. разд. 13.1.4), стандартные функции интерполяции-экстраполяции стоит применять только в непосредственной близости границ интервала данных. В Mathcad имеется более развитый инструмент экстраполяции, который учитывает распределение данных вдоль всего интервала. В функцию predict встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляции:
predict (у,m, n) — функция предсказания вектора, экстраполирующего выборку данных:
у — вектор действительных значений, взятых через равные промежутки значений аргумента; m — количество последовательных элементов вектора у, согласно которым строится экстраполяция; n — количество элементов вектора предсказаний.
Пример использования функции предсказания на примере экстраполяции осциллирующих данных уj с меняющейся амплитудой приведен в листинге 13.4. Полученный график экстраполяции, наряду с самой функцией, показан на рис. 13.10. Аргументы и принцип действия функции predict отличаются от рассмотренных выше встроенных функций интерполяции-экстраполяции. Значений аргумента для данных не требуется, поскольку по определению функция действует на данные, идущие друг за другом с равномерным шагом. Обратите внимание, что результат функции predict вставляется "в хвост" исходных данных.
Листинг 13.4. Экстраполяция при помощи функции предсказания
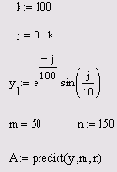
Как видно из рис. 13.11, функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данных результат часто бывает неудовлетворительным. Кроме того, функция
predict хорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью (типа рис. 13.10), в основном осциллирующего характера.

Рис. 13.10. Экстраполяция при помощи функции предсказания (продолжение листинга 13.4)

Рис. 13.11. Работа функции предсказания в случае малого количества данных (продолжение листинга 13.5)
Если данных мало, то предсказание может оказаться бесполезным. В листинге 13.5 приведена экстраполяция небольшой выборки данных (из примеров, рассмотренных в предыдущих разделах). Соответствующий результат показан на рис. 13.11 для различных крайних точек массива исходных данных, для которых строится экстраполяция.
Листинг 13.5. Экстраполяция при помощи функции предсказания

Глава 13.1.6. Многомерная интерполяция
Двумерная сплайн-интерполяция приводит к построению поверхности z (х,у), проходящей через массив точек, описывающий сетку на координатной плоскости
(х,у). Поверхность создается участками двумерных кубических сплайнов, являющихся функциями
(х,у) и имеющих непрерывные первые и вторые производные по обеим координатам.
Многомерная интерполяция строится с помощью тех же встроенных функций, что и одномерная (см. разд. 13.1.2), но имеет в качестве аргументов не векторы, а соответствующие матрицы. Существует одно важное ограничение, связанное с возможностью интерполяции только квадратных
NxN массивов данных:
interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами:
s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline; х — матрица размерности Nх2, определяющая диагональ сетки значений аргумента (элементы обоих столбцов соответствуют меткам х и у и расположены в порядке возрастания); z — матрица действительных данных размерности NxN; v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
ПРИМЕЧАНИЕ
Вспомогательные функции построения вторых производных имеют те же матричные аргументы, что и interp:
lspline (X, Y), pspline (X, Y), cspline (X, Y).
Пример исходных данных приведен на рис. 13.12 в виде графика линий уровня, программная реализация двумерной интерполяции показана в листинге 13.6, а ее результат — на рис. 13.13.
Листинг 13.6. Двумерная интерполяция


Рис. 13.12. Исходное двумерное поле данных (продолжение листинга 13.6)

Рис. 13.13. Результат двумерной интерполяции (продолжение листинга 13.6)
Глава 13.2. Регрессия
Задачи математической регрессии имеют смысл приближения выборки данных (xi,yi) некоторой функцией f(x), определенным образом минимизирующей совокупность ошибок |f(xi)-yil. Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость f (х). В силу производимого действия большинство задач регрессии являются частным случаем более общей проблемы сглаживания данных.
Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных
(xi,yi).
Глава 13.2.1. Линейная регрессия
Самый простой и наиболее часто используемый вид регрессии — линейная. Приближение данных (xi,yi) осуществляется линейной функцией у(х) = =b+ах. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 13.14). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты
а и b вычисляются из условия минимизации суммы квадратов ошибок
|b+axi-yi|.
ПРИМЕЧАНИЕ 1
Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных
(xi,yi) другими зависимостями
у(х). Исключение рассмотрено в листинге 13.9.
ПРИМЕЧАНИЕ 2
Различным расчетным аспектам реализации метода наименьших квадратов, в большинстве случаев сводящимся к решению систем алгебраических линейных уравнений, была посвящена значительная часть главы 8.
Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа. Правила их применения представлены в листингах 13.7 и 13.8. Результат обоих листингов получается одинаковым (рис. 13.14):
line (х, у) — вектор из двух элементов (b,а) коэффициентов линейной регрессии b+ах; intercept (х, у) — коэффициент ь линейной регрессии; slope (x,y) — коэффициент а линейной регрессии:
Листинг 13.7. Линейная регрессиях — вектор действительных данных аргумента; у — вектор действительных данных значений того же размера.
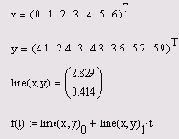
Листинг 13.8. Другая форма записи линейной регрессии


Рис. 13.14. Линейная регрессия (продолжение листинга 13.7 или 13.8)
В Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную регрессию для расчета коэффициентов
а и b (листинг 13.9):
medfit(x,y) — вектор из двух элементов (b,а) коэффициентов линейной медиан-медианной регрессии b-ах:
Листинг 13.9. Построение линейной регрессии двумя разными методами (продолжение листинга 13.7)х, у — векторы действительных данных одинакового размера.

Различие результатов среднеквадратичной и медиан-медианной регрессии иллюстрируется на рис. 13.15.

Рис. 13.15. Линейная регрессия по методу наименьших квадратов и методу медиан (продолжение листингов 13.7 и 13.9)
Глава 13.2.2. Полиномиальная регрессия
В Mathcad реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.
Полиномиальная регрессия
Полиномиальная регрессия означает приближение данных (xi,yi) полиномом
k-й степени A(x)=a+bx+cx2+dx3+.. .+hxk
(рис. 13.16). При k=i полином является прямой линией, при k=2 — параболой, при
k=3 — кубической параболой и т. д. Как правило, на практике применяются
k<5.
ПРИМЕЧАНИЕ
Для построения регрессии полиномом k-й степени необходимо наличие, по крайней мере,
(k+1) точек данных.
В Mathcad полиномиальная регрессия осуществляется комбинацией встроенной функции
regress и полиномиальной интерполяции (см. разд. 13.1.2):
regress (х, у, k) — вектор коэффициентов для построения полиномиальной регрессии данных; interp(s,x,y, t) — результат полиномиальной регрессии:
s=regress(х,у,k); x — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; у — вектор действительных данных значений того же размера; k — степень полинома регрессии (целое положительное число); t — значение аргумента полинома регрессии;
ВНИМАНИЕ!
Для построения полиномиальной регрессии после функции regress вы обязаны использовать функцию interp
.

Рис. 13.16. Регрессия полиномами разной степени (коллаж результатов листинга 13.10 для разных k)
Пример полиномиальной регрессии квадратичной параболой приведен в листинге 13.10.
Листинг 13.10. Полиномиальная регрессия

Регрессия отрезками полиномов
Помимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т. к. они имеют криволинейную форму) нескольких полиномов. Для этого имеется встроенная функция
loess, применение которой аналогично функции regress (листинг 13.11
и рис. 13.17):
loess (х, у, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов; interp(s,x,y,t) — результат полиномиальной регрессии:
s=loess(х,у,span); х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; у — вектор действительных данных значений того же размера; span — параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span=0.75).
Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (например, span=2 дает почти тот же результат, что и приближение точек параболой).
Листинг 13.11. Регрессия отрезками полиномов

СОВЕТ
Регрессия одним полиномом эффективна, когда множество точек выглядит как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.

Рис. 13.17. Регрессия отрезками полиномов (продолжение листинга 13.11)
Двумерная полиномиальная регрессия
По аналогии с одномерной полиномиальной регрессией и двумерной интерполяцией (см. разд. 13.1.5), Mathcad позволяет приблизить множество точек Zi,j(xi,yj) поверхностью, которая определяется многомерной полиномиальной зависимостью. В качестве аргументов встроенных функций для построения полиномиальной регрессии должны стоять в этом случае не векторы, а соответствующие матрицы.
regress (x,z,k) — вектор коэффициентов для построения полиномиальной регрессии данных. loess (x, z, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов. interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами.
s — вектор вторых производных, созданный одной из сопутствующих функций loess или regress. х — матрица размерности Nx2, определяющая пары значений аргумента (столбцы соответствуют меткам х и у). z — вектор действительных данных размерности N. span — параметр, определяющий размер отрезков полиномов. k — степень полинома регрессии (целое положительное число). v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
ВНИМАНИЕ!
Для построения регрессии не предполагается никакого предварительного упорядочивания данных (как, например, для двумерной интерполяции, которая требует их представления в виде матрицы
NxN). В связи с этим данные представляются как вектор.
Двумерная полиномиальная регрессия иллюстрируется листингом 13.12 и рис. 13.18. Сравните стиль представления данных для двумерной регрессии с представлением тех же данных для двумерной сплайн-интерполяции (см. листинг 13.6) и ее результаты с исходными данными (см. рис. 13.12) и их сплайн-интерполяцией (см. рис. 13.13).

Рис. 13.18. Двумерная полиномиальная регрессия (продолжение листинга 13.12)
Листинг 13.12. Двумерная полиномиальная регрессия

ПРИМЕЧАНИЕ
Обратите внимание на знаки транспонирования в листинге. Они применены для корректного представления аргументов (например, z, в качестве вектора, а не строки).
Глава 13.2.3. Другие типы регрессии
Кроме рассмотренных, в Mathcad встроено еще несколько видов трехпараметрической регрессии. Их реализация несколько отличается от приведенных выше вариантов регрессии тем, что для них, помимо массива данных, требуется задать некоторые начальные значения коэффициентов а,
b, с. Используйте соответствующий вид регрессии, если хорошо представляете себе, какой зависимостью описывается ваш массив данных. Когда тип регрессии плохо отражает последовательность данных, то ее результат часто бывает неудовлетворительным и даже сильно различающимся в зависимости от выбора начальных значений. Каждая из функций выдает вектор уточненных параметров а,
b, с.
expfit (х, у, g) — регрессия экспонентой f (х) =aebx+c. igsfit (x,y,g) — регрессия логистической функцией f (x)=a/ (1+bе-сх). sinfit (x,y,g) — регрессия синусоидой f (x) =a-sin (х+b) +с. pwfit(x,y,g) — регрессия степенной функцией f (х)=а-хb+с. logfit (х, у, g) — регрессия логарифмической функцией f (x)=aln(x+b) +c. infit (x,y) — регрессия двухпараметрической логарифмической функцией f (x)=aln(x)+b.
х — вектор действительных данных аргумента. у — вектор действительных значений того же размера. g — вектор из трех элементов, задающий начальные значения а, b, с.
ПРИМЕЧАНИЕ
Правильность выбора начальных значений можно оценить по результату регрессии — если функция, выданная Mathcad, хорошо приближает зависимость у (х), значит, они были подобраны удачно.
Пример расчета одного из видов трехпараметрической регрессии (экспоненциальной) приведен в листинге 13.13 и на рис. 13.19. В предпоследней строке листинга выведены в виде вектора вычисленные коэффициенты а, ь, с, а в последней строке через эти коэффициенты определена искомая функция f (х) .

Рис. 13.19. Экспоненциальная регрессия (продолжение листинга 13.13)
Листинг 13.13. Экспоненциальная регрессия
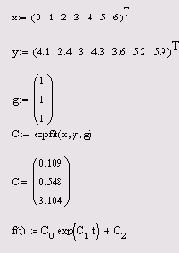
ПРИМЕЧАНИЕ
Многие задачи регрессии данных различными двухпараметрическими зависимостями у(х) можно свести к более надежной, с вычислительной точки зрения, линейной регрессии. Делается это с помощью соответствующей замены переменных.
Глава 13.2.4. Регрессия общего вида
В Mathcad можно осуществить регрессию в виде линейной комбинации C1f1(x)+C2f2(x) + ..., где
fi(x) — любые функции пользователя, a Ci — подлежащие определению коэффициенты. Кроме того, имеется путь проведения регрессии более общего вида, когда комбинацию функций и искомых коэффициентов задает сам пользователь.
Приведем встроенные функции для регрессии общего вида и примеры их использования (листинги 13.14 и 13.15), надеясь, что читатель при необходимости найдет более подробную информацию об этих специальных возможностях в справочной системе и Ресурсах Mathcad.
Unfit (х, у, F) — вектор параметров линейной комбинации функций пользователя, осуществляющей регрессию данных. genfit (х, у, g, G) — вектор параметров, реализующих регрессию данных с помощью функций пользователя общего вида.
х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания. у — вектор действительных значений того же размера. F(x) — пользовательская векторная функция скалярного аргумента. g — вектор начальных значений параметров регрессии размерности N. G(x,C) — векторная функция размерности N+1, составленная из функции пользователя и ее N частных производных по каждому из параметров C.
ПРИМЕЧАНИЕ
Число данных (количество элементов в векторах х и у) должно быть не меньше, чем N. Это менее жесткое требование появилось в Mathcad 12, а до этого
для функции регрессии общего вида genfit было необходимо задание не менее N+1 данных.
Листинг 13.14. Регрессия линейной комбинацией функций пользователя

Листинг 13.15. Регрессия общего вида
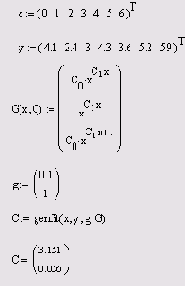
Глава 13.3. Ввод/вывод данных
Завершим главу, посвященную интерполяции и регрессии, реализации в Mathcad функции ввода/вывода во внешние файлы, поскольку, как правило, анализ данных чаще всего связан с их импортом из внешних источников (например, результатов эксперимента из текстовых или графических файлов) и экспортом на внешние носители. В большинстве случаев ввод внешних данных в документы Mathcad применяется чаще вывода, поскольку Mathcad имеет гораздо лучшие возможности представления результатов расчетов, чем многие пользовательские программы. Для общения с внешними файлами данных в Mathcad имеет несколько разных способов, причем в но-( вой 12-й версии добавлены новые, намного более удобные опции импорта.
Глава 13.3.1. Ввод/вывод в текстовые файлы
Перечислим встроенные функции для работы с текстовыми файлами, которые имеются в Mathcad 2001—12.
ПРИМЕЧАНИЕ
В Mathcad 12 имеется дополнительная универсальная встроенная функция READFILE, значительно облегчающая процесс импорта данных.
READPRN("fiie") — чтение данных в матрицу из текстового файла. WRITEPRN("file") — запись данных в текстовый файл. APPENDPRN ("file") — дозапись данных в существующий текстовый файл:
file — путь к файлу.
ПРИМЕЧАНИЕ
Можно задавать как полный путь к файлу, например, С:\Мои документы, так и относительный, имея в виду, что он будет отсчитываться от папки, в которой находится файл с документом Mathcad. Если вы задаете в качестве аргумента просто имя файла (как в листингах 13.16—13.17), то файл будет записан или прочитан из той папки, в которой находится сам документ Mathcad.
Примеры использования встроенных функций иллюстрируются, листингами 13.16—13.18. Результат действия листингов 13.16 и 13.18 можно понять, просмотрев получающиеся текстовые файлы, например, с помощью Блокнота Windows (рис. 13.20 и 13.21 соответственно).
Листинг 13.16. Запись матрицы в текстовый файл

Листинг 13.17. Чтение данных из текстового файла в матрицу

Листинг 13.18. Дозапись вектора k в
существующий текстовый файл


Рис. 13.20. Файл, созданный листингом 13.16

Рис. 13.21. Файл, созданный листингами 13.16 и 13.18
Обратите внимание, что, если вы выводите данные в файл, пользуясь встроенной функцией
WRITEPRN, то в любом случае создается новый текстовый файл. Если даже до записи данных файл с таким именем существовал, то его содержимое будет уничтожено, заменившись новыми данными. Если вы хотите сохранить прежнее содержимое текстового файла с данными, пользуйтесь функцией
APPENDPRN. Эта встроенная функция может применяться и для создания нового файла. Иными словами, если файла с заданным именем не существовало, то он будет создан и наполнен теми данными, которые вами определены в документе.
ПРИМЕЧАНИЕ
Создание нового файла путем использования функции APPENDPRN добавлено разработчиками только в версии Mathcad 11. В прежних версиях программы попытка добавить данные к несуществующему файлу при помощи этой функции вызовет сообщение об ошибке.
Глава 13.3.2. Ввод/вывод в файлы других типов
Подобно вводу/выводу в текстовые файлы можно организовать чтение и запись данных в графические звуковые и файлы.
Графические файлы
При записи и чтении числовой информации в файлы различных графических форматов данные отождествляются с интенсивностью того или иного цвета пиксела изображения, находящегося в файле. Перечислим основные встроенные функции, предназначенные для графического ввода/вывода:
READRGB("fiie") — чтение цветного изображения; READBMP("file") — чтение изображения в оттенках серого; WRiTERGB("fiie") — запись цветного изображения; WRiTEBMP("fiie") — запись изображения в оттенках серого:
file — путь к файлу.
ПРИМЕЧАНИЕ
Имеется также большое количество функций специального доступа к графическим файлам, например, чтение интенсивности цветов в других цветовых моделях (яркость-насыщенмость-оттенок), а также чтение только одного из основных цветов и т. п. Вы без труда найдете информацию об этих функциях в справочной системе Mathcad, а их применение полностью эквивалентно описанным встроенным функциям.
Действие функций доступа к графическим файлам иллюстрируется листингами 13.19—13.21. Заметим, что для создания изображения используется встроенная функция
identity, создающая единичную матрицу. Изображение, созданное листингом 13.19, приведено на рис. 13.22.
Листинг 13.19. Запись матрицы I в
графический файл


Рис. 13.22. Файл, созданный листингом 13.19
Листинг 13.20. Чтение из графического файла

Листинг 13.21. Запись в цветной графический файл

Звуковые файлы
Начиная с версии Mathcad 2001, появилась возможность записывать и считывать амплитуду акустических сигналов в звуковые файлы с расширением wav.
READWAV("fiie") — чтение звукового файла в матрицу. WRiTEWAV("file", s,b) — запись данных в звуковой файл. GETWAViNFO("fiie") — создает вектор из четырех элементов с информацией о звуковом файле.
file — путь к файлу. s — скорость следования сэмплов, задаваемых матрицей. b — разрешение звука в битах.
Использование этих встроенных функций позволяет организовать обработку звука.
Анимация
Во многих случаях самый зрелищный способ представления результатов математических расчетов — это анимация. В Mathcad очень просто создавать анимационные ролики и сохранять их в видеофайлах.
Основной принцип анимации в Mathcad — покадровая анимация. Ролик анимации — это просто последовательность кадров, представляющих собой некоторый участок документа, который выделяется пользователем. Расчеты производятся обособленно для каждого кадра, причем формулы и графики, которые в нем содержатся, должны быть функцией от номера кадра. Номер кадра задается системной переменной FRAME, которая может принимать лишь натуральные значения. По умолчанию, если не включен режим подготовки анимации, FRAME=0.
Рассмотрим последовательность действий для создания ролика анимации, например, демонстрирующего перемещение гармонической бегущей волны. При этом каждый момент времени будет задаваться переменной FRAME.
1. Введите в документ необходимые выражения и графики, в которых участвует переменная номера кадра FRAME. Подготовьте часть документа, которую вы желаете сделать анимацией, таким образом, чтобы она находилась в поле вашего зрения на экране. В нашем примере подготовка сводится к определению функции f (x,t) :=sin(x-t) и созданию ее декартова графика у (х, FRAME) .
2. Выполните команду Tools / Animation / Record (Сервис / Анимация / Запись).
3. В диалоговом окне Record Animation (Анимация) задайте номер первого кадра в поле From (От), номер последнего кадра в поле То (До) и скорость анимации в поле At (Скорость) в кадрах в секунду (рис. 13.23).
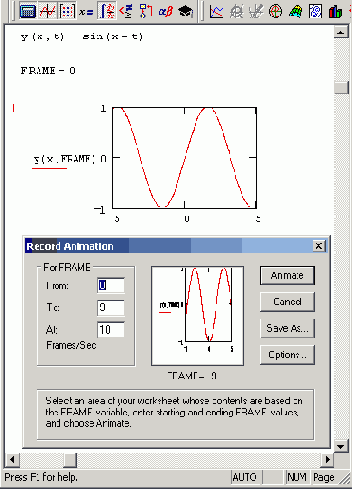
Рис. 13.23. Начало создания анимации
4. Выделите протаскиванием указателя мыши при нажатой левой кнопке мыши область в документе, которая станет роликом анимации.
5. В диалоговом окне Record Animation (Анимация) нажмите кнопку Animate (Анимация). После этого в окошке диалогового окна
Record Animation (Анимация) будут появляться результаты расчетов выделенной области, сопровождающиеся выводом текущего значения переменной
FRAME. По окончании этого процесса на экране появится окно проигрывателя анимации (рис. 13.24).
6. Запустите просмотр анимации в проигрывателе нажатием кнопки воспроизведения в левом нижнем углу окна проигрывателя.
7. В случае если вид анимации вас устраивает, сохраните ее в виде видеофайла, нажав кнопку
Save As (Сохранить как) в диалоговом окне Record Animation (Анимация). В появившемся диалоговом окне
Save Animation (Сохранить анимацию) обычным для Windows способом укажите имя файла и его расположение на диске.
8. Закройте диалог Record Animation (Анимация) нажатием кнопки Cancel (Отмена) или кнопки управления его окном.

Рис. 13.24. Просмотр созданного ролика анимации
После того как вы сохранили видеофайл, его можно использовать за пределами Mathcad. Скорее всего, если вы, находясь в обозревателе Windows, дважды щелкнете на имени этого файла, он будет загружен в проигрыватель видеофайлов Windows, и вы увидите его на экране компьютера. Таким образом, запуская видеофайлы в обычном проигрывателе, вы имеете возможность устроить красочную презентацию результатов вашей работы как на своем, так и на другом компьютере.
ПРИМЕЧАНИЕ
При создании файлов анимации допускается выбирать программу видеосжатия (кодек) и качество компрессии. Делается это с помощью кнопки
Options (Опции) в диалоговом окне Record Animation (Анимация).
Глава 13.3.3. Мастер импорта данных и функция READFILE
В Mathcad 12 появились две новых, более универсальных, возможности для импорта данных из внешнего файла. Они связаны с появлением Мастера импорта данных, позволяющего осуществить импорт в нужном формате в диалоговом режиме с подсказками, а также новой встроенной функции
READFILE, призванной унифицировать процесс импорта. Первый путь позволяет импортировать данные "вручную", проследив процесс считывания данных последовательно, шага за шагом, а второй — автоматизировать его, не путаясь в других многочисленных функциях импорта.
ПРИМЕЧАНИЕ
Оба способа подразумевают возможность импорта файлов данных самых разных форматов: текстовых с разнообразными символами-разделителями, а также файлы формата xls (Microsoft Excel).
Рассмотрим реализацию первой возможности на примере считывания данных из файла, представленного ранее на рис. 13.20 и 13.21 и в листингах 13.16 и 13.17 (см. разд. 13.3.1):
1. Введите команду меню Insert / Component (Вставка / Компонент), а затем выберите в списке тип компонента
Data Import Wizard (Мастер импорта данных). В результате появится окно Мастера, которое в пошаговом диалоговом режиме позволит осуществить считывание нужной информации (рис. 13.25).
2. Выберите в раскрывающемся списке File format (Формат файла) желаемый формат файла, из которого вы осуществляете импорт (рис. 13.26). Если вы затрудняетесь с его точной идентификацией, лучшим решением будет задание типа Delimited Text (Текст с разделителями), что позволит возложить распознавание типа данных и формат их записи на Mathcad.
3. Нажмите кнопку Browse (Пролистать) и отыщите в открывшемся диалоговом окне местоположение нужного вам файла.
4. Если вы уверены (например, основываясь на накопленном опыте работы с Мастером импорта), что данные будут считаны правильно, то можете сразу нажать кнопку
Finish (Завершить). Если вы хотите просмотреть и, при необходимости, изменить те или иные опции импорта, нажмите кнопку
Next (Вперед). В последнем случае в диалоговом режиме еще на двух страницах Мастера (подобных рис. 13.26, но с новыми параметрами) можно будет отредактировать многочисленные параметры импорта (такие как тип разделителя между данными, интервалы импорта и т. д.).

Рис. 13.25. Стартовая страница окна Data Import Wizard
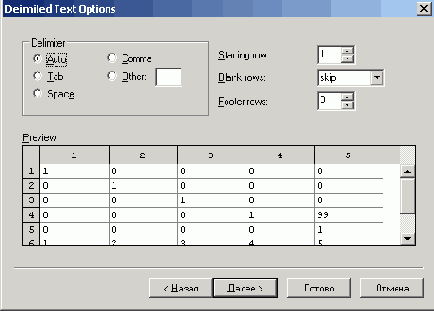
Рис. 13.26. Следующая страница окна Data Import Wizard
5. После нажатия кнопки Finish (Завершить) в диалоге Data Import Wizard
(Мастер импорта данных) и возвращения на рабочую область документа Mathcad введите в местозаполнитель, появившийся слева от таблицы импортированных данных, желаемое имя переменной. В дальнейших расчетах ее можно будет использовать как обычную матрицу.
Итог работы Мастера показан на рис. 13.27. Его первая строка является результатом описанных шагов по считыванию данных в матрицу, а вторая строка показывает вывод этой матрицы в стандартной для Mathcad форме.

Рис. 13.27. Результат импорта данных из файла
Новая функция READFILE облегчает процесс "программного" считывания данных из файла (листинг 13.22):
READFILE ("file","type",[colwidth,rows,cols,emptyfill]) — возвращает матрицу с элементами, считанными из внешнего файла данных:
Листинг 13.22. Импорт данных при помощи универсальной функции READFILE"file" — название файла (включая путь к нему на диске); "type" — тип файла ("delimited" или "Excel"); colwidth — ширина столбца данных, считываемого из файла в случае выбора в качестве предыдущего параметра типа "fixed", т. е. с фиксированной шириной данных; rows — начальная строка импорта данных или двухкомпонентный вектор, задающий интервал импорта строк; cols — начальный столбец импорта данных или двухкомпонентный вектор, задающий интервал импорта столбцов; emptyfill — значение, которое будет использовано для замены отсутствующих данных (пустот в файле). Для него можно использовать значение НеЧисло (NaN) (см. разд. 1.2.5).
