Математические задачи в пакете MathCAD 12
Глава 14.1. Фурье-спектр
Интегральные преобразования массива сигнала у(х) ставят в соответствие всей совокупности данных
у(х) некоторую функцию другой координаты F(v). Рассмотрим встроенные функции для расчета интегральных преобразований, реализованных в Mathcad.
Математический смысл преобразования Фурье состоит в представлении сигнала у(х) в виде бесконечной суммы синусоид вида
F(v)sin(v-x). Функция F(V) называется преобразованием Фурье, или интегралом Фурье, или Фурье-спектром сигнала. Ее аргумент
v имеет смысл частоты соответствующей составляющей сигнала. Обратное преобразование Фурье переводит спектр
F(V) в исходный сигнал у (х). Согласно определению,

Как видно, преобразование Фурье является комплексной величиной, даже если сигнал действительный.
Глава 14.1.1. Фурье-спектр действительных данных
Преобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм, называемый БПФ (быстрое преобразование Фурье). Рассмотрим сначала наиболее типичную для физического эксперимента ситуацию расчета Фурье-спектра действительного сигнала, для которой алгоритм БПФ реализован в нескольких встроенных функциях Mathcad, различающихся нормировками:
fft (у) — вектор прямого преобразования Фурье; FFT (у) — вектор прямого преобразования Фурье в другой нормировке:
у — вектор действительных данных, взятых через равные промежутки значений аргумента.
ВНИМАНИЕ!
Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно
2n элементов (n— целое число). Результатом является вектор с
1+2n-1 элементами. Если число данных не совпадает со степенью
2, то необходимо дополнить недостающие элементы нулями, иначе вместо решения появится сообщение об ошибке.

Рис. 14.1. Исходные модельные данные (продолжение листинга 14.1)
Чтобы смысл преобразования Фурье был более понятен, используем в качестве модельных данных дискретизацию детерминированного сигнала,, равного сумме трех синусоид (рис. 14.1). Листинг 14.1 демонстрирует расчет Фурье-спектра по
N=128 точкам, причем предполагается, что интервал дискретизации данных yi равен
Δ. В середине листинга применяется встроенная функция
fft, а его оставшаяся часть предназначена для корректного пересчета соответствующих значений частот
Ωi (они вычисляются в последней строке листинга). Обратите внимание, что результаты расчета представляются в виде модуля Фурье-спектра (рис. 14.2), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра (рис. 14.3) с определением синусоид в листинге 14.1.
Листинг 14.1. Быстрое преобразование Фурье


Рис. 14.2. Матрица-результат вычисления Фурье-спектра данных (продолжение листинга 14.1)
Исключительно важными представляются два параметра, заданные в предпоследней строке листинга 14.1, называемые соответственно граничной частотой и частотой Найквиста. Граничная частота
Ω0 определяет нижнюю, а частота Найквиста
ΩN — верхнюю границу аргумента вычисленного спектра, как показано маркерами на рис. 14.3. Кроме того, важно, что интервал дискретизации Фурье-спектра также равен
Ω0, а общее число вычисляемых
точек спектра составляет N/2 (в нашем примере N/2=64). Последние утверждения иллюстрируются маркерами на рис. 14.4, изображающем график Фурье-спектра вблизи нижней границы частот.
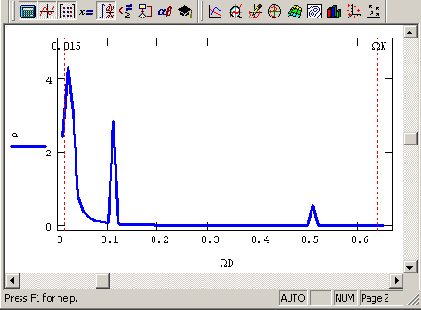
Рис. 14.3. График Фурье-спектра данных (продолжение листинга 14.1)

Рис. 14.4. Низкочастотная область Фурье-спектра (продолжение листинга 14.1)
Глава 14.1.2. Обратное преобразование Фурье
Для расчета обратного Фурье-преобразования (восстановления сигнала по имеющемуся действительному спектру) следует использовать следующие встроенные функции (они также реализуют алгоритм БПФ):
ifft (v) — вектор обратного действительного преобразования Фурье; IFFT(V) — вектор обратного действительного преобразования Фурье в другой нормировке:
v — вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.
ПРИМЕЧАНИЕ
Аргумент (вектор v) функций, реализующих обратное преобразование Фурье, может быть как действительным, так и комплексным. А вот результат их работы является вектором, составленным из действительных чисел. Если аргумент является N-компонентным вектором, где
N=l+2n, то в результате получается в два раза больший вектор из 2 (N-1) =2n+1 компонент.
Результат обратного преобразования Фурье спектра, представленного на рис. 14.2 и 14.3, показан в виде кружков на рис. 14.5 вместе с исходными данными.

Рис. 14.5. Обратное преобразование Фурье (продолжение листинга 14.1)
Видно, что в рассматриваемом случае сигнал у(х) восстановлен с большой точностью, что характерно для плавного изменения сигнала. Если же в качестве аргумента функции
ifft использовать модуль Фурье-спектра (мы присвоили этому вектору в листинге 14.1 имя а), то профиль исходного сигнала будет реконструирован правильно, но окажется сдвинутым на определенное расстояние вдоль оси х. Так происходит из-за того, что взятие абсолютной величины комплексного спектра уничтожает информацию об относительной фазе отсчетов данных.
Глава 14.1.3. Преобразование Фурье комплексных данных
Алгоритм быстрого преобразования Фурье для комплексных данных встроен в соответствующие функции, в имя которых входит литера "с":
cfft (у) — вектор прямого комплексного преобразования Фурье; CFFT(y) — вектор прямого комплексного преобразования Фурье в другой нормировке; icfft(y) — вектор обратного комплексного преобразования Фурье; ICFFT(V) — вектор обратного комплексного преобразования Фурье в другой нормировке:
у — вектор данных, взятых через равные промежутки значений аргумента; v — вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.
Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля, и выводят только его половину (см. разд. 14.1. Г). Поэтому, в частности, по 128 действительным данным получалось всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье (рис. 14.6), то получится вектор из 128 элементов. Сравнивая рис. 14.3 и 14.6, можно уяснить соответствие между результатами действительного и комплексного Фурье-преобразования.
Листинг 14.2. Комплексное быстрое преобразование Фурье (продолжение листинга 14.1)


Рис. 14.6. Комплексное преобразование Фурье (продолжение листинга 14.2)
Глава 14.1.4. Пример: артефакты дискретного Фурье-преобразования
При численном нахождении преобразования Фурье следует очень внимательно относиться к таким важнейшим параметрам, как объем выборки (в терминах листинга 14.1,
xМАХ) и интервал дискретизации (Δ). Соотношение этих двух величин определяет диапазон частот (Ω0,ΩN), для которых возможно вычисление значений Фурье-спектра. В этой связи хотелось бы обратить внимание на три типичные опасности, которые могут подстерегать неподготовленного исследователя при расчете дискретного Фурье-преобразования и быть для него весьма неожиданными.
Влияние конечности интервала выборки
Во-первых, следует обратить внимание на само определение преобразования Фурье как интеграла с бесконечными пределами. Его численное отыскание подразумевает принципиальную ограниченность интервала интегрирования (просто в силу конечности объема выборки). Поэтому самым очевидным несоответствием будет поиск, вообще говоря, другого интеграла, отличного от интеграла Фурье. Влияние конечности интервала выборки проявляется главным образом на искажении его низкочастотной области. В качестве примера приведем Фурье-спектр гармонической функции с частотой 0.015. Для его расчета достаточно заменить в листинге 14.1 четвертую строку на равенство
yi:=sin(2π0.915xi). Соответствующий Фурье-спектр изображен на рис. 14.7 (сверху — в обычном, а снизу — в более крупном масштабе) и демонстрирует не совсем правильное поведение в низкочастотной области. Как видно, спектр содержит довольно широкий максимум вместо одиночного пика, как было в случае средних частот сигнала на рис. 14.3.
ПРИМЕЧАНИЕ 1
Если быть точным, вместо спектра некоторой функции f (х) дискретное преобразование Фурье подразумевает вычисление спектра другой функции
f (х)Ф(х), где Ф(х) — это функция-ступенька, равная единице в пределах расчетного интервала и нулю за его пределами. В частотной области это соответствует операции свертки означенных двух функций, что, конечно, искажает (неизвестный) точный спектр
f (х). Для борьбы с проявлением конечности интервала выборки используются специальные методы, основанные на применении техники спектральных окон.
ПРИМЕЧАНИЕ 2
Из сказанного ясно, почему исследователя не должна смущать необходимость
дополнения массива исходных данных нулями до размера 2" (чтобы можно было
использовать алгоритм БПФ). По самому определению дискретного Фурье-преобразования, исходная функция и так предполагается равной нулю за пределами расчетного интервала, что приводит к неминуемым искажениям.

Рис. 14.7. Иллюстрация влияния конечности выборки на расчет низкочастотной части Фурье-спектра
Сдвиг ноль-линии
Еще одним, наиболее ярким, проявлением вредного влияния конечности интервала выборки может служить расчет Фурье-преобразования суммы гармонического сигнала и константы (рис. 14.8). Для того чтобы получить данный рисунок, достаточно еще слегка (по сравнению с рис. 14.7) модифицировать строку листинга, касающуюся определения компонент вектора у, добавив к нему i:
yi:=sin(2π0.915xi)+1.
Сравнивая рис. 14.7 и 14.8, несложно догадаться, почему так разительно изменился вид спектра в низкочастотной области. Пугающий рост спектра на левом крае частотного интервала объясняется совокупностью двух факторов: конечности выборки и добавлением к сигналу ненулевой постоянной составляющей (так называемым сдвигом ноль-линии). Сумма сигнала и константы определяет соответствующее влияние на вычисленный спектр, который также оказывается (просто в силу линейности операции интегрирования) суммой спектров сигнала и ступенчатой функцией (равной той самой константе внутри расчетного интервала и нулю за его пределами).

Рис. 14.8. Фурье-спектр суммы гармонического сигнала и константы (влияние конечности выборки)

Рис. 14.9. Расчеты Фурье-спектров гармонических сигналов с разной частотой
("маскировка частот")
Избавиться от искажений, вызванных сдвигом ноль-линии, довольно просто. Достаточно (до Фурье-преобразования) вычислить среднее значение выборки и затем вычесть его из каждого элемента выборки. Если после этой операции вычислить Фурье-спектр, то он окажется примерно таким, как показано на рис. 14.7.
Маскировка частот
Еще один классический пример ошибочного расчета Фурье-спектра связан с возможным присутствием в сигнале гармоник с частотой, превышающей частоту Найквиста, в данном примере
ΩN=0.б4 (см. разд. 14.1.Г). Иллюстрация эффекта, называемого "маскировкой частот", приведена на рис. 14.9, который содержит расчет спектров трех различных синусоидальных сигналов с разной частотой
f0. Первый спектр сигнала с частотой, меньшей частоты Найквиста, вычислен верно, а вот два остальных спектра показывают, что в случае превышения частоты Найквиста в спектре начинают присутствовать "лишние" пики. Появление артефактов спектра связано с тем, что дискретных отсчетов начинает не хватать для того, чтобы прописать высокочастотные гармоники с достаточной информативностью.
ПРИМЕЧАНИЕ
Напоминаем, что все листинги, имеющиеся в книге, а также документы Mathcad с расчетами всех рисунков, вы найдете на прилагаемом компакт-диске.
Глава 14.1.5. Пример: спектр модели сигнал/шум
Пока мы использовали в качестве примера детерминированный сигнал, представляющий собой сумму трех синусоид. Несмотря на единство термина "дискретное преобразование Фурье", прикладное применение спектрального анализа можно довольно четко разделить на две категории.
Сигнал, подвергающийся спектральному анализу, получен в условиях пренебрежимо малой погрешности, т. е. его можно, фактически, считать детерминированным. Такая ситуация характерна для экспериментальной оптики и (разного рода) спектроскопии. В этом случае для большинства задач анализа сигналов бывает вполне достаточно использовать простые спектры Фурье, рассмотренные выше (см. разд. 14.1.1—14.1.3). Сигнал, полученный в присутствии значительной шумовой компоненты, которая существенно искажает его структуру. В этом случае следует говорить о смеси (к счастью, чаще всего аддитивной) "полезный сигнал + шум", причем в большинстве случаев заранее известна некоторая информация о статистике шумовой компоненты. Данная ситуация очень часто встречается в экспериментальной геофизике и радиофизике. В этом случае подходить к интерпретации спектров следует с вероятностной точки зрения. Как раз этому вопросу мы и посвятим данный пример.
Фурье-спектр
Внесем минимальное добавление в расчеты листинга 14.1, а именно добавим к его четвертой строке (в которой определяется
yi) еще одно (четвертое) слагаемое: псевдослучайную величину
σrnd(1), где значение 1/σ характеризует отношение сигнал/шум. Явный вид изменений, которые следует внести в листинг 14.1, приведен на рис. 14.10, наряду с графиком сигнала
у(х). Расчет Фурье-спектра данного сигнала (в соответствии с алгоритмом, представленным выше, см. листинг 14.1) показан на рис. 14.11. Как видно, присутствие шумовой компоненты может значительно искажать спектр сигнала и затруднять его интерпретацию.
ПРИМЕЧАНИЕ
Максимальное значение спектра на левом крае частотного интервала является ни чем иным, как проявлением искажающего влияния конечности выборки и сдвига ноль-линии (см. разд. 14.1.3), произошедшим из-за внесения шума с математическим ожиданием, равным
0.5.

Рис. 14.10. Модель сигнал / шум

Рис. 14.11. График Фурье-спектра данных
Спектр мощности
В силу стохастичности исходных данных, представляющих сумму полезного сигнала и шума, сами вычисленные значения спектра Фурье носят также случайный характер. В этой связи необходимо знать, с какой погрешностью они рассчитываются. Однако из курса математической статистики известно, что для обычного Фурье-преобразования случайного сигнала (в частности, нормального) не найдено оценок для погрешности. Это слабое место Фурье-спектров делает их практически неприменимыми для анализа случайных сигналов, а вместо них надо применять так называемые спектры мощности (или, по-другому, энергетические спектры), для которых указанные оценки существуют.
Не углубляясь в теорию математической статистики, приведем пример вычисления спектра мощности сигнала (рис. 14.10), основанный его определении. Как известно, спектром мощности сигнала называют Фурье-преобразование его корреляционной функции. Таким образом, алгоритм расчета спектра мощности сводится к следующему: во-первых, вычислению автокорреляционной функции (рис. 14.12); во-вторых, ее прореживанию и (или) сглаживанию (в целях уменьшения влияния конечности выборки); и, наконец, в-третьих, расчету ее Фурье-преобразования. Результат вычисления спектра мощности (листинг 14.3) в соответствии с приведенным сценарием показан на рис. 14.13.
ПРИМЕЧАНИЕ 1
Аналогичным образом, через Фурье-преобразование взаимной корреляционной функции, определяются взаимные спектры мощности двух выборок.
ПРИМЕЧАНИЕ 2
Еще один способ вычисления спектров мощности, не требующий расчета функции корреляции, приведен ниже (см. разд. 14.3.6).
ПРИМЕЧАНИЕ 3
Методика расчета в Mathcad корреляционной функции случайного процесса обсуждалась в главе 12 (см. разд. 12.3.3).
Листинг 14.3. Расчет спектра мощности для модели сигнал/шум


Рис. 14.12. Автокорреляционная функция
модельной зависимости сигнал / шум
(продолжение листинга 14.3)

Рис. 14.13. График спектра мощности данных
модельной зависимости сигнал / шум
(продолжение листинга 14.3)
Глава 14.1.6. Двумерный спектр Фурье
В Mathcad имеется возможность применять встроенные функции комплексного преобразования Фурье не только к одномерным, но и к двумерным массивам, т. е. матрицам. Соответствующий пример приведен в листинге 14.4 и на рис. 14.14 в виде графика линий уровня исходных данных и рассчитанного Фурье-спектра.
Листинг 14.4. Двумерное преобразование Фурье

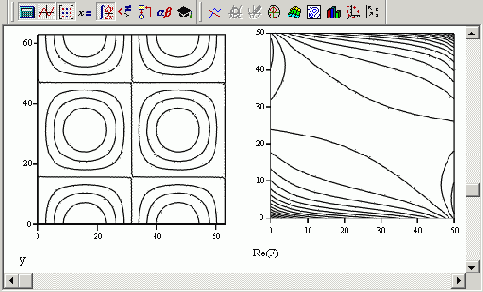
Рис. 14.14. Данные (слева) и их Фурье-спектр (справа) (продолжение листинга 14.4)
Глава 14.2. Вейвлет-спектры
В последнее время возрос интерес к другим интегральным преобразованиям, в частности, вейвлет-преобразованию
(или дискретному волновому). Оно применяется, главным образом, для анализа нестационарных сигналов и для многих задач подобного рода оказывается более эффективным, чем преобразование Фурье. Основным отличием вейвлет-преобразования является разложение данных не по синусоидам (как для преобразования Фурье), а по другим функциям, называемым вейвлетобразующими. Вейвлетобразующие функции, в противоположность бесконечно осциллирующим синусоидам, локализованы в некоторой ограниченной области своего аргумента, а вдали от нее равны нулю или ничтожно малы. Пример такой функции, называемой "мексиканской шляпой", показан на рис. 14.15.

Рис. 14.15. Сравнение синусоиды и вейвлетобразующей функции
Из-за своего математического смысла вейвлет-спектр имеет не один аргумент, а два. Помимо частоты, вторым аргументом ь является место локализации вейвлетобразующей функции. Поэтому
b имеет ту же размерность, что и х.
Глава 14.2.1. Встроенная функция вейвлет-преобразования
Mathcad имеет одну встроенную функцию для расчета вейвлет-преобразования на основе вейвлетобразующей функции Добеши:
wave (у) — вектор прямого вейвлет-преобразования; iwave (v) — вектор обратного вейвлет-преобразования:
у — вектор данных, взятых через равные промежутки значений аргумента; v — вектор данных вейвлет-спектра.
Аргумент функции вейвлет-преобразования, т. е. вектор у, должен так же, как и в преобразовании Фурье, иметь ровно 2n элементов (n — целое число). Результатом функции wave является вектор, скомпонованный из нескольких коэффициентов с двухпараметрического вейвлет-спектра. Использование функции wave объясняется на примере анализа суммы двух синусоид в листинге 14.5, а три семейства коэффициентов вычисленного вейвлет-спектра показаны на рис. 14.16.
Листинг 14.5. Поиск вейвлет-спектра Добеши


Рис. 14.16. Вейвлет-спектр на основе функции Добеши (продолжение листинга 14.5)
Глава 14.2.2. Программирование вейвлет-преобразований
Наряду со встроенной функцией wave Mathcad снабжен пакетом расширения для осуществления вейвлет-анализа. Пакет расширения содержит большое число дополнительных встроенных функций, имеющих отношение к вейвлет-преобразованиям. Обзор пакетов расширения выходит за рамки данной книги, поэтому ограничимся простым упоминанием об этой возможности. Напомним, что дополнительную информацию об использовании данных встроенных функций можно найти в соответствующей электронной книге, которую можно открыть при помощи меню
Help / E-Books / Wavelet extension pack (Справка / Электронные книги / Вейвлет-анализ данных).
Помимо встроенной функции вейвлет-спектра Добеши и возможностей пакета расширения Mathcad, возможно непосредственное программирование алгоритмов пользователя для расчета вейвлет-спектров. Оно сводится к аккуратному расчету соответствующих семейств интегралов. Один из примеров такой программы приведен в листинге 14.6, а ее результат на рис. 14.17. Анализу подвергается та же функция, составленная из суммы двух гармонических функций, сильно различающихся по частоте. Сам график двухпара-метрического вейвлет-спектра
с(а,b) на плоскости (а,b) выведен в виде привычных для вейвлет-анализа линий уровня.
Листинг 14.6. Поиск вейвлет-спектра на основе "мексиканской
шляпы"

ПРИМЕЧАНИЕ
Программа листинга очень проста, но исключительно далека от хорошей в смысле быстродействия. Каждый интеграл вычисляется независимо, без использования методов ускорения, типа применяемых в алгоритме БПФ. Однако простые приемы программирования вполне доступно раскрывают математический смысл вейвлет-преобразования.
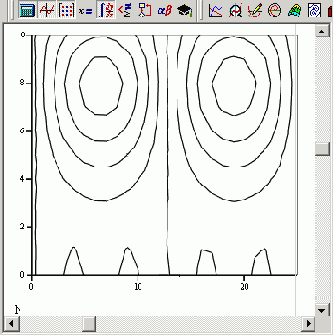
Рис. 14.17. Вейвлет-спектр на основе "мексиканской шляпы" (продолжение листинга 14.6)
Глава 14.3. Сглаживание и фильтрация
При анализе данных часто возникает задача их фильтрации, заключающаяся в устранении одной из составляющих зависимости
y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые чаще всего обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая. В связи с этим считают, что
сглаживание является частным случаем более общей задачи фильтрации сигнала, которая связана с подавлением определенных диапазонов частот спектра.
Наиболее простым и эффективным рецептом сглаживания (smoothing) можно считать регрессию различного вида, разобранную в предыдущей главе (см. разд. 13.2). Однако регрессия часто уничтожает информативную составляющую данных, оставляя лишь наперед заданную пользователем зависимость.
Часто рассматривают противоположную задачу фильтрации — устранение медленно меняющихся вариаций в целях исследования высокочастотной составляющей. В этом случае говорят о задаче устранения тренда. Иногда интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением полосовой фильтрации.
Несколько примеров программной реализации различных вариантов фильтрации приведены в данном разделе.
Глава 14.3.1. Встроенные функции для сглаживания: ВЧ-фильтр
В Mathcad имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных:
medsmooth(y,b) — сглаживание алгоритмом "бегущих медиан"; ksmooth (х, у, b) — сглаживание на основе функции Гаусса; supsmooth(x,y) — локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных:
х — вектор действительных данных аргумента (для supsmooth его элементы должны быть расположены в порядке возрастания); у — вектор действительных значений того же размера, что и х; b — ширина окна сглаживания.
Все функции имеют в качестве аргумента векторы, составленные из массива данных, и выдают в качестве результата вектор сглаженных данных того же размера. Функция medsmooth предполагает, что данные расположены равномерно.
ПРИМЕЧАНИЕ
Подробную информацию об алгоритмах, заложенных в функции сглаживания, вы найдете в справочной системе Mathcad в статье
Smoothing (Сглаживание),
находящейся в разделе Statistics (Статистика). Очень полезные сведения о разных типах фильтрации можно отыскать в Быстрых шпаргалках.
Часто бывает полезным совместить сглаживание с последующей интерполяцией или регрессией. Соответствующий пример приведен в листинге 14.7 для функции
supsmooth. Результат работы листинга показан на рис. 14.18 (кружки обозначают исходные данные, крестики — сглаженные, пунктирная кривая — результат сплайн-интерполяции). Сглаживание тех же данных при помощи "бегущих медиан" и функции Гаусса с разным значением ширины окна пропускания показаны на рис. 14.19 и 14.20 соответственно.
Листинг 14.7. Сглаживание с последующей сплайн-интерполяцией


Рис. 14.18. Адаптивное сглаживание (продолжение листинга 14.7)

Рис. 14.19. Сглаживание "бегущими медианами"

Рис. 14.20. Сглаживание при помощи функции ksmooth
Глава 14.3.2. Скользящее усреднение: ВЧ-фильтр
Помимо встроенных в Mathcad, существует несколько популярных алгоритмов сглаживания, на одном из которых хочется остановиться особо. Самый простой и очень эффективный метод — это скользящее усреднение. Его суть состоит в расчете для каждого значения аргумента среднего значения по соседним
w данным. Число w называют окном скользящего усреднения; чем оно больше, тем больше данных участвуют в расчете среднего, тем более сглаженная кривая получается. На рис. 14.21 показан результат скользящего усреднения одних и тех же данных (кружки) с разным окном
w=3 (пунктир), w=5 (штрихованная кривая) и w=l5 (сплошная кривая). Видно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших
w — отражают лишь закономерность их медленных вариаций.
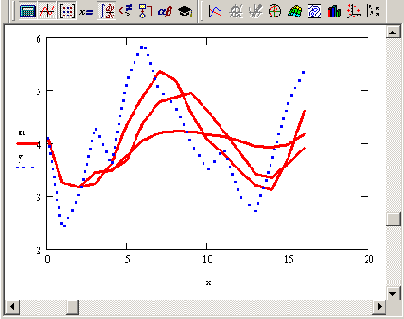
Рис. 14.21. Скользящее усреднение с разными w=3, 5,15 (листинг 14.8, коллаж трех графиков)
Чтобы реализовать в Mathcad скользящее усреднение, достаточно очень простой программы, приведенной в листинге 14.8. Она использует только значения у, оформленные в виде вектора, неявно предполагая, что они соответствуют значениям аргумента
х, расположенным через одинаковые промежутки. Вектор х применялся лишь для построения графика результата (рис. 14.21).
Листинг 14.8. Сглаживание скользящим усреднением

ПРИМЕЧАНИЕ
Приведенная программная реализация скользящего усреднения самая простая, но не самая лучшая. Возможно, вы обратили внимание, что все кривые скользящего среднего на рис. 14.21 слегка "обгоняют" исходные данные. Почему так происходит, понятно: согласно алгоритму, заложенному в последнюю строку листинга 14.8, скользящее среднее для каждой точки вычисляется путем усреднения значений предыдущих
w точек. Чтобы результат скользящего усреднения был более адекватным, лучше применить центрированный алгоритм расчета по
w/2 предыдущим и w/2 последующим значениям. Он будет немного сложнее, поскольку придется учитывать недостаток точек не только в начале (как это сделано в программе с помощью функции условия if), но и в конце массива исходных данных.
Глава 14.3.3. Устранение тренда: НЧ-фильтр
Еще одна типичная задача возникает, когда интерес исследований заключается не в
анализе медленных (или низкочастотных) вариаций сигнала у(х) (для чего
применяется сглаживание данных), а в анализе быстрых его изменений. Часто
бывает, что быстрые (или высокочастотные) вариации накладываются определенным
образом на медленные, которые обычно называют трендом. Часто тренд имеет заранее
предсказуемый вид, например, линейный. Чтобы устранить тренд, можно предложить последовательность действий, реализованную в листинге 14.9.
1. Вычислить регрессию f (х), например, линейную, исходя из априорной информации о тренде (предпоследняя строка листинга).
2. Вычесть из данных у(х) тренд f (х) (последняя строка листинга).
Листинг 14.9. Устранение тренда

На рис. 14.22 показаны исходные данные (кружками), выделенный с помощью регрессии линейный тренд (сплошной прямой линией) и результат устранения тренда (пунктир, соединяющий крестики).

Рис. 14.22. Устранение тренда (продолжение листинга 14.9)
Глава 14.3.4. Полосовая фильтрация
В предыдущих разделах была рассмотрена фильтрация быстрых вариаций сигнала (сглаживание) и его медленных вариаций (снятие тренда). Иногда требуется выделить среднемасштабную составляющую сигнала, уменьшив как более быстрые, так и более медленные его компоненты. Одна из возможностей решения этой задачи связана с применением полосовой фильтрации на основе последовательного скользящего усреднения.
Алгоритм Полосовой фильтрации приведен в листинге 14.10, а результат его применения показан на рис. 14.23 сплошной кривой. Алгоритм реализует такую последовательность операций:
1. Выставление ноль-линии, т. е. приведение массива данных у к нулевому среднему значению путем его вычитания из каждого элемента у (третья и четвертая строки листинга).
2. Устранение из сигнала у высокочастотной составляющей, имеющее целью получить сглаженный сигнал
middle, например, с помощью скользящего усреднения с малым окном w (в листинге 14.10
w=3).
3. Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном
w (в листинге 14.9 w=7), либо с помощью снятия тренда (см. разд. 14.3.3).
4. Вычесть из сигнала middle тренд slow (последняя строка листинга), тем самым выделяя среднемасштабную составляющую исходного сигнала
у.
Листинг 14.10. Полосовая фильтрация


Рис. 14.23. Результат полосовой фильтрации (продолжение листинга 14.10)
Глава 14.3.5. Спектральная фильтрация
Альтернативой всем представленным до сих пор алгоритмам, в частности, методу полосовой фильтрации (см. предыдущий разд.) является фильтрация на основе интеграла Фурье. Пока мы использовали для подавления в сигнале тех или иных частотных диапазонов определенные процедуры, основанные на арифметических преобразованиях. Между тем, для той же цели (правда, с большими вычислительными затратами) можно применять методы Фурье-анализа. Действительно, если вычислить спектр сигнала, удалить из него (или существенно уменьшить) определенные частоты, а затем выполнить обратное преобразование Фурье, то результатом будет фильтрованный сигнал.
Пример фильтрации на основе преобразования Фурье приведен в листинге 14.11. В качестве модельного сигнала использовалась смесь двух гармонических сигналов и равномерно распределенного шума (рис. 14.24). Фурье-спектр данных
z, вычисленный при помощи встроенной функции fft, показан на рис. 14.25. Листинг 14.11 отличается от листинга 14.1 (см. разд. 14.1. Г), главным образом, последними двумя строками, в которых, собственно, и определяется явный вид спектрального фильтра
w(Ω), или, по-другому, спектральное окно. Обратное Фурье-преобразование спектра произведения спектрального окна
w(Ω) и Фурье-спектра сигнала
z, представляющее собой результат фильтрации, показано на рис. 14.24 сплошной кривой.
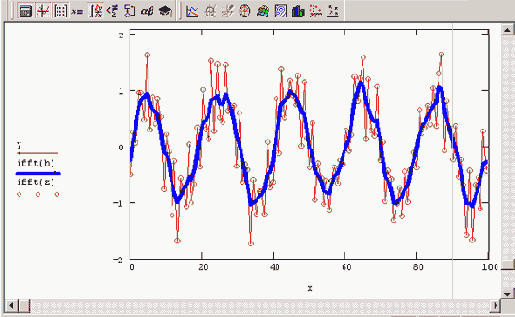
Рис. 14.24. Исходный модельный сигнал (кружки)
и результат его фильтрации на основе Фурье-преобразования
(продолжение листинга 14.11)
Листинг 14.11. Фильтрация на основе преобразования Фурье


Рис. 14.25. Фурье-преобразование модельного сигнала
и спектральное окно-фильтр
(продолжение листинга 14.11)
Глава 14.3.6. Пример: вычисление спектра мощности
Завершим главу, посвященную спектральному анализу, еще одним примером вычисления спектра мощности (его определение приведено в разд. 14.1.5) модельного сигнала, связанного с использованием его Фурье-спектра. В листинге 14.12 сначала выполняется преобразование Фурье суммы гармонического сигнала и шума (распределенного равномерно), а затем (в трех последних строках листинга) производится его сглаживание путем скользящего усреднения с окном, равным
3. Из курса математической статистики известно, что квадратная степень сглаженного преобразования Фурье может считаться оценкой спектра мощности, и для вычисленного таким образом спектра уже можно применять вероятностные оценки погрешностей его отсчетов. Результаты работы листинга 14.12 (Фурье- и энергетический спектр) показаны на рис. 14.26 (кружками и сплошной кривой соответственно).
Листинг 14.12. Вычисление спектра мощности

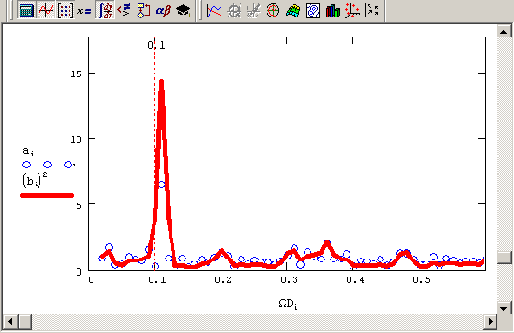
Рис. 14.26. Фурье-преобразование модельного сигнала
и его спектр мощности (продолжение листинга 14.12)