Алгебра и пакет Mathematica 5
Матрицы
В системе Mathematica матрицы представляются в виде списков строк, т.е. в виде списков списков. Вот пример задания матрицы. Матрица задается как список списков.
m1={{1,1,1,1},{а,Ь,с,d},{а^2,b^2,с^2,d^2}}
{{1,1,1,1},
{а,b,с,d}, {а2,b2,с2,d2}}
Конечно, привычнее ее видеть как матрицу.

Действия с матрицами и векторами задаются естественным образом. Умножим, например, матрицу на вектор.
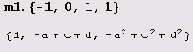
А вот как можно умножить матрицу m1 на скаляр t.
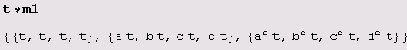
Для квадратной матрицы Mathematica позволяет найти определитель, а также обратную матрицу (если, конечно, матрица обратима, т.е. имеет ненулевой определитель), собственные значения и векторы.
Пусть

Найдем определитель
Det[m2]
2
Поскольку он ненулевой, можем найти обратную матрицу.
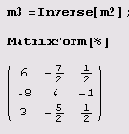
Произведение матрицы на ее обратную должно быть единичной матрицей. Давайте проверим.
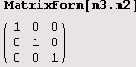
Так и есть!
Однако обратите внимание: произведение матриц обозначается точкой. Дело в том, что произведение m3 * m2 тоже имеет смысл, но это поэлементное произведение списков, а не произведение матриц! Убедимся в этом.
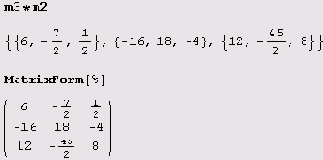
Собственные значения и векторы находятся без особых сложностей.
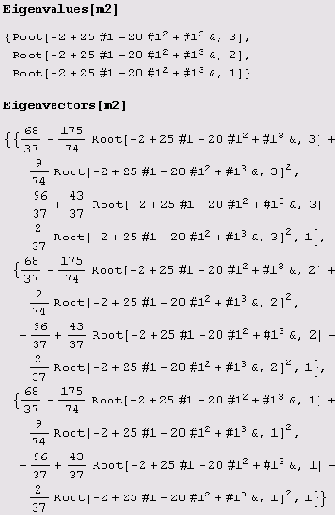
Да, пока не совсем понятно... Но не огорчайтесь, при необходимости собственные числа и собственные векторы можно найти приближенно. Вот как найти ответ с машинной точностью.

Но все же, что же это такое `Root? Оказывается, Root[f, k] — это k-й корень алгебраического уравнения f [#1] = 0. (Таким образом, f — полином.) Так что, система Mathematica умеет решать уравнения?! Оказывается, да!