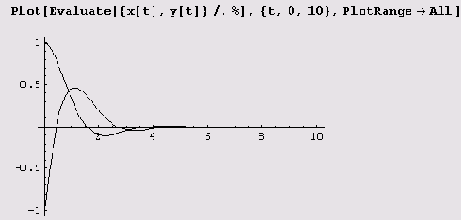Алгебра и пакет Mathematica 5
Уравнения
Система Mathematica классно решает разнообразные уравнения и их системы.
В системе Mathematica знак равенства (=) в уравнениях представляется посредством
двойного знака равенства (= =). Вот как можно решить уравнение х3 + х - 2 = 0.
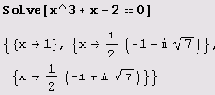
Обратите внимание на мнимую единицу в записи двух корней. Как видите, был найден не только вещественный корень, но и комплексные корни. Система Mathematica находит все (вещественные и комплексные) решения алгебраических уравнений степени не выше 4, притом не только с числовыми коэффициентами, но и с параметром.
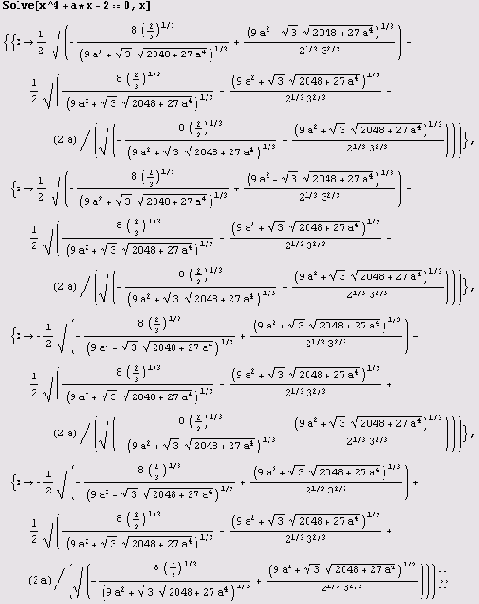
Конечно, ответ несколько громоздкий. Представьте, если бы вам пришлось искать его самостоятельно!
Решения общего алгебраического уравнения степени 5 или выше через радикалы не выражаются, но всегда могут быть найдены численные их значения. Тем не менее система Mathematica пытается найти точное решение. Например, уравнение х5 + х - 2 = 0 система Mathematica решит точно.
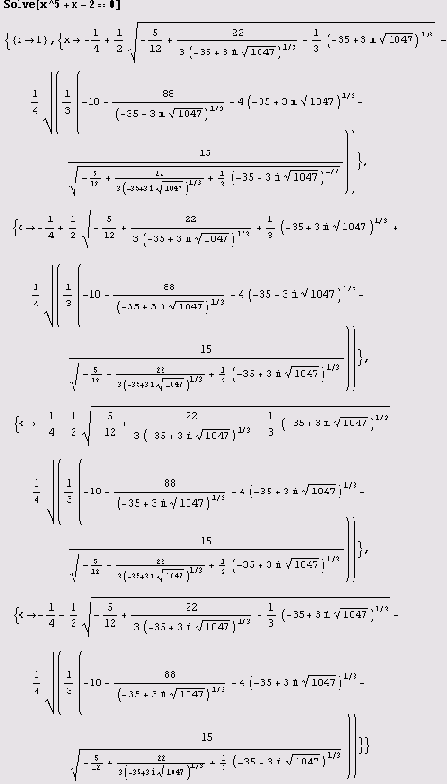
А вам слабо? Давайте попробуем решить уравнение х5 + х -7 = 0 .
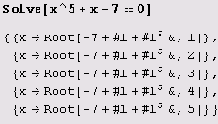
Да, корни уравнения — это его корни... (И, как видите, их пять, что тоже не особенно информативно, если учесть, что многочлен пятой степени.) В данном случае при необходимости можно решить уравнение численно.
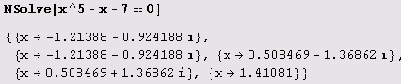
Чтобы решить трансцендентное уравнение, нужно задать начальное приближение к корню. Вот как, например, можно решить уравнение cosx = 2x.
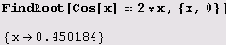
Давайте попробуем решить систему линейных алгебраических уравнений.
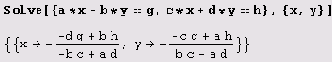
А чтобы решить систему трансцендентных уравнений, нужно задать начальные приближения неизвестных.
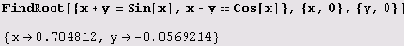
Система Mathematica умеет решать и дифференциальные уравнения и их системы.
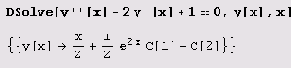
Как видите, решение содержит произвольные постоянные C [1] и С [2]. Можно найти также численное решение задачи Коши для дифференциальных уравнений или их систем.
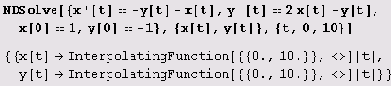
Правда, решение содержит приближенную функцию (объект InterpolatingFunction). Но этот объект может быть вычислен, как и любой другой объект системы Mathematica. В частности, можно построить график.