Алгебра и пакет Mathematica 5
Представление вещественных чисел систематическими дробями: функция N. Разрядность и точность вещественных чисел: функции Precision и Accuracy .
Оказывается, что если вместо целого числа указать равное ему вещественное (для этого достаточно поставить десятичную точку в записи числа), то в результате также будет записано вещественное число с десятичной точкой.
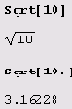
Более того, существует конвертор (преобразователь), который представляет вещественные числа, а также вещественную и мнимую части комплексных чисел в виде десятичной дроби. Таким конвертором является функция N.
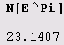
При необходимости разрядность можно указать и явно: у функции N имеется второй, необязательно указываемый аргумент, который определяет разрядность чисел, используемую при вычислении результата. Если второй аргумент не задан, то по умолчанию в вычислениях используется $MachinePrecision цифр, причем результат выводится с шестью цифрами. Например, ниже вычисляется 50 десятичных знаков
π.
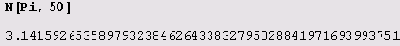
При вычислениях с вещественными числами очень полезны функции Precision и
Accuracy, названия которых можно перевести как разрядность и точность. Разрядность вещественного числа — это количество значащих десятичных цифр в нем, а точность — это количество значащих десятичных цифр в его дробной части. При
вычислениях система Mathematica считает, что вещественные числа имеют либо машинную (по умолчанию), либо неопределенную (произвольную) разрядность. Для того чтобы узнать машинную разрядность компьютера, достаточно вычислить выражение $MachinePrecision. (В версии 5 системы Mathematica имеется также
константа MachinePrecision, которая равна значению выражения $MachinePrecision.) На разных типах компьютеров это выражение, конечно, может принимать разные значения. На современных ПК оно обычно близко к 16.
$MachinePrecision
15.9546
Значения функций Precision и Accuracy для целых и рациональных чисел равны Infinity.
Если вводится менее $MachinePrecision цифр вещественного числа, то считается, что его разрядность равна $MachinePrecision.
Если количество введенных цифр вещественного числа превышает $MachinePrecision, то его разрядность равна количеству введенных цифр.
Ниже показаны способы задания разрядности и точности при внешнем представлении вещественных чисел. Для задания численного значения разрядности и точности используется знак `.
Число с машинной разрядностью: 123.4
Число с произвольной разрядностью (на некоторых машинах): 123.45678901234567890
Число с машинной разрядностью (на всех машинах): 123.45678901234567890`
Число с произвольной разрядностью 200 десятичных знаков: 123. 456`200
Число с произвольной разрядностью и точностью 200 десятичных знаков: 123.456`200
Число с машинной разрядностью в экспоненциальной форме: 1.234*^6
Число в экспоненциальной форме с разрядностью 200: 1.234`200*^6
Число в двоичной системе с разрядностью 200: 2^^101.111`200
Число в двоичной системе в экспоненциальной форме: 2^^101.111`200*^6
Ниже приведены примеры, показывающие, как задание разрядности и точности влияет на представление результатов.

При вычислениях отслеживается точность и разрядность результата. Поэтому функцию N часто вызывают для вычисления численных значений выражений, в частности констант.

Встроенные в систему Mathematica алгоритмы обладают тем свойством, что при вычислении функции N от констант все цифры результата получаются верными. Однако в общем случае не следует ожидать, что все n цифр результата вычисления выражения N[ехрr, n] верные. Справедливо лишь то, что вычисления велись с разрядностью не менее n.
Поскольку комплексные числа можно рассматривать как пары вещественных чисел, аргументами функций N, Precision и Accuracy могут быть и комплексные числа.