Алгебра и пакет Mathematica 5
Дробная часть вещественного числа: функция FractionalPart
Пусть х — вещественное число. Тогда его дробную часть {х} можно определить равенством: {х} = х - [х]. По этому, общепринятому в математике определению дробная часть всегда неотрицательна и меньше единицы: 0<{х}<1. Однако в системе Mathematica используется несколько иное определение:
FractionalPart[х] = х - IntegerPart[х].
Поэтому FractionalPart [х] отрицательна для нецелых отрицательных х.
Чтобы освоиться с функцией FractionalPart, напишем программу, которая распечатывает результат применения функции FractionalPart к каждому элементу списка. Прежде всего нам понадобится определить функцию, которая оформляет вывод следующим образом.
FractionalPart[ х ]- результат применения функции FractionalPart к х
Вот как для этого можно определить функцию f.
f=(Print["FractionalPart[",#1,"]=",FractionalPart[#1]] &)
Теперь можем написать программу, в которой функция f применяется к каждому элементу списка.
f/@{x,2.4,0.3999999999999999',2.6,0.6000000000000001\-2.4,
-0.3999999999999999",-2.6,Pi,10,-Рi^2,2*Sin[1],Ехр[Pi*Sqrt[163]]}
Вот результат
Давайте теперь вычислим
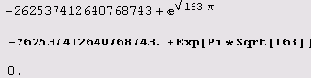
Неужели число
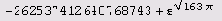
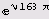целое. Давайте повторим вычисления.
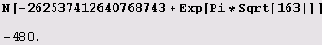
О, это уже какая-то загадка. Разные результаты при вычислении одного и того же выражения! А вот и разгадка: мы проводили вычисления с разной разрядностью, притом в обоих случаях точность была недостаточна. Давайте повторим вычисления с большей разрядностью.
Теперь мы видим, что
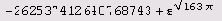-13! Между прочим, когда
системы компьютерной алгебры не были столь доступны, как сейчас, число е√163π доставляло немало хлопот не только студентам, но и многим вполне серьезным "дядям и тетям", недостаточно знакомым с признаками трансцендентности чисел. Некоторые
шутники с вполне серьезным видом заявляли, что все говорит о том, что число е является целым, но никто этого пока не доказал, и что за доказательство обещана кругленькая сумма и т.д. А ведь чтобы прямым вычислением установить ложность этого высказывания, необходимо было провести вычисления более чем с 30 десятичными знаками! Даже вычислить его целую часть на машинах серии JBM/360 или БЭСМ-6 без ухищрений было невозможно! Конечно, на зарубежных машинах были доступны системы компьютерной алгебры, например MACSYMA на IBM/360. Однако на территории СССР доступ к таким системам имели весьма немногие. Кроме того, в советской системе образования следствием застойных явлений были ориентация на идеологические дисциплины (история КПСС, разнообразный марксизм и т.д.), отсутствие свободно выбираемых (студентом, а не деканатом!) курсов и сохранение подчиненной роли курса алгебры (всего три семестра) на уровне прошлого века. В советских университетах даже для студентов-математиков программой не было предусмотрено знакомство с современной алгеброй. О компьютерной алгебре не слышали и многие преподаватели. Поэтому на территории СССР вера в необходимость прямого вычисления с довольно большим количеством значащих цифр была не простым заблуждением обывателя, а подкреплялась советской системой образования. Поэтому именно те, кто был заинтересован в финансировании произвольноразрядной арифметики, и устраивали такие розыгрыши, предварительно тщательно выискивая потенциальных жертв. Фактически из отечественных машин для проверки гипотезы подходили только машины серии МИР. Но машина МИР-1, во входном языке (Алмир) которой была реализована произвольноразрядная арифметика, имела память объемом всего лишь 4 Кбайт, а машина МИР-2 — 8 Кбайт, причем быстродействие машины МИР-2 из-за частой сборки мусора падало подчас до 200 операций в секунду! Тем не менее благодаря встроенному языку Аналитик, в котором была реализована произвольноразрядная арифметика и элементы компьютерной алгебры, она справлялась с задачами, одна лишь постановка которых на БЭСМ-6 была весьма трудоемка, и потому очередь к этой машине стояла в десятки раз больше, чем за колбасой. А поскольку заранее никто не мог сказать, сколько времени потребуется на вычисление, спланировать его не представлялось возможным. Что же касается машины МИР-3 (особенно модели МИР-32), то фактически она была доступна только разработчикам, из числа которых
и находились самые злостные шутники'! Кстати, в те годы системы компьютерной алгебры часто не могли определить, является ли заданное число алгебраическим. Начиная с версии 4 в системе Mathematica не составляет труда записать (и вычислить!) нужный предикат.
Ехр[ Pi*Sqrt[163]]sAlgebraics
False
Всякая история имеет мораль, и эта не исключение: вычисляя дробную часть, не забывайте указывать нужную разрядность и, кроме того, не упускайте из виду цель, ради которой вы проводите вычисления, — подумайте, нельзя ли достичь цели более простым способом. (Мы бы, например, могли сразу спросить систему Mathematica, является ли е√163πалгебраическим числом.) Не забывайте также о том, что подчас с помощью систем компьютерной алгебры удается разрешить вопрос, который остается открытым в течение длительного времени. Впрочем, иногда достаточно вспомнить всего лишь несколько теорем.
Упражнение 3.1. Вычислите не менее k десятичных цифр числа я, начиная с n-й после десятичной точки. Можете ли вы провести вычисления, например, для n = 100 000, k = 1000? Иными словами, можете ли вы вычислить сто первую тысячу (после запятой) знаков в представлении этого числа десятичной дробью?
Решение. Вот самое простое решение, которое обычно приходит в голову неискушенному читателю. Сначала нужно вычислить п с разрядностью, которая гарантирует n + k + 1 верную цифру, например n + k + 10, а затем в полученной дроби выбрать нужные десятичные знаки. Что касается вычисления я с разрядностью хотя бы 101001, то оно для системы Mathematica никакого труда не представляет. Но вот что касается отсчитать сто тысяч знаков после запятой... Впрочем, в системе Mathematica и для этого предусмотрены нужные функции! Но если немного поразмыслить, то окажется, что решить поставленную задачу можно с помощью функции FractionalPart, "Ну, я об этом сразу догадался!" — высокомерно воскликнет искушенный читатель. Действительно, чего же можно было еще ожидать, если этот раздел посвящен функции FractionalPart? Ну разве что каких-либо трудностей при составлении программы. Но ее составить как раз совсем нетрудно.
n=100000; k=1000; m= N[FractionalPart[10^ (n-1)*Pi],k+10]
Правда, ее нужно предварительно. проверить. Это совсем просто, достаточно уменьшить значения пик, затем провести вычисления
n=1; k=5; m= N[FractionalPart[10^(n-1)*Pi],k+10]
0.141592653589793
n=2; k=5; m= N[FractionalPart [10^(n-1)*Pi],k+10]
0.415926535897932
n=10; k=5; m= N[FractionalPart[10^(n-1)*Pi],k+10]
0.589793238462643и сверить результаты с таблицами. Как легко убедиться, результаты совпадают, так что беспокоиться вроде бы не о чем. Но вот если положить n = 50, появляется предупреждение о недостаточной разрядности.
N::meprec: Internal precision limit $MaxExtraPrecision =50.
reached while evaluating -
31415926535897«21»841971693993751«1» «1» .
А при n = 1000 результат выглядит вообще странно: 0.х1034, да и предупреждений целых два! Давайте разберемся, в чем тут дело. Для этого придется проанализировать ход вычислений. Сначала вычисляется Pi с некоторой точностью, притом с запасом (не более $MaxExtraPrecision десятичных знаков, как следует из предупреждения), а затем это число умножается на степень 10, так что в итоге получается 10^ (n-l) *Pi с некоторой точностью, после чего мы пытаемся взять у этого полученного числа его дробную часть. Но вот теперь и оказывается, что число было вычислено с недостаточной точностью, и система Mathematica предупреждает об этом! Впрочем, выход очевиден: нужно просто увеличить значение $MaxExtraPrecision. Но увеличение будет весьма значительным, и потому лучше всего сделать так, чтобы увеличенное значение $MaxExtraPrecision использовалось системой Mathematica только при вычислении результата, нужного для функции FractionalPart. Иными словами, увеличенное значение $MaxExtraPrecision нужно сделать локальным. Для этого достаточно воспользоваться функцией Block. Тогда можно написать следующую тестовую программу.
Do[Block[{k=10},Block[{$MaxExtraPrecision = n+k+10),
Print[n+1,":",N[FractionalPart[10^n*Рi],k+10]]]],{n,0,2030,5}]
Едва ли стоит полностью приводить распечатку результата, но вот отдельные ее части явно заслуживают обсуждения. Вот банальное начало, подтверждающее правильность задания в программе степеней, умножений и всей подобной тривиальной чепухи, в записи которой так легко допустить ошибку.
1 : 0.14159265358979323846
6 : 0.26535897932384626434
11 0.89793238462643383280
16 0.23846264338327950288
21 0.26433832795028841972
26 0.83279502884197169399
31 0.50288419716939937511
36 0.41971693993751058210
Правильность цифр можно проверить по таблицам, имеющимся почти в любом солидном справочнике по математике или в какой-нибудь монографии, посвященной арифметике произвольной разрядности, например во втором томе бессмертного труда Дональда Кнута Искусство программирования. Что касается продолжения распечатки, то в ней правильность цифр проверить уже сложнее. Ведь найти книгу с более чем пятидесятые знаками л существенно сложнее. Из опыта знаю, что на территории СССР научному сотруднику, не связанному со спецслужбами вроде КГБ или ГРУ, получить доступ к серьезному фолианту по истории вычисления я практически было невозможно. Тем больше наша благодарность организатору первых математических олимпиад в Ленинграде (и СССР; первые олимпиады в Москве и Киеве проводились только через год) Василию Августовичу Кречмару, который в последних изданиях своего труда Задачник по алгебре (предназначенного для любознательных школьников!) поместил результат вычисления л с 2035 знаками после запятой. Разрабатывая арифметику произвольной разрядности для различных программных комплексов (в том числе и систем компьютерной алгебры), я при проверке получаемых результатов неоднократно пользовался шестым изданием этого бестселлера. Вполне подойдет эта книга и для проверки (хотя бы и выборочной) результатов, выдаваемых нашей программой. Так что можем читать нашу распечатку дальше.
41 0.69399375105820974945
46 0.37510582097494459231
51 0.58209749445923078164
56 0.74944592307816406286
61 0.59230781640628620900
66 0.78164062862089986280
71 0.062862089986280348253
76 0.20899862803482534212
81 0.86280348253421170680
86 0.34825342117067982148
91 0.34211706798214808651
96 0.70679821480865132823
101 : 0.82148086513282306647
106 : 0.086513282306647093845
Вы заметили, что распечатан один "лишний" знак? А знаете, почему? Продолжаем читать дальше.
111 : 0.32823066470938446096
116 : 0.066470938446095505822
121 : 0.093844609550582231725
И вот опять появились "лишние" знаки. Правда, и в этом случае после точки стоит сразу 0. Но не случайность ли это?
126 : 0.46095505822317253594
131 : 0.50582231725359408128
136 : 0.23172535940812848112
141 : 0.53594081284811174503
146 : 0.081284811174502841027
И вот опять появился "лишний" знак. И опять после точки стоит сразу 0. Да не закономерность ли это? Давайте пропустим часть распечатки и поищем еще "лишние" знаки (я выделяю их курсивом, знак после точки — полужирным).
286 0.60726024914127372459
291 0.024914127372458700661
296 0.41273724587006606316
301 0.72458700660631558817
306 0.70066063155881748815
311 0.063155881748815209210
316 0.58817488152092096283
356 0.90360011330530548820
361 0.011330530548820466521
366 0.053054882046652138415
371 0.48820466521384146952
416 0.91953092186117381933
421 0.092186117381932611793
426 0.61173819326117931051
О, действительно, это, должно быть, закономерность. Итак, мы полагаем, что если после точки идет нуль, то вычисляется дополнительная цифра. Ну а если нулей несколько? Может быть, количество ведущих нулей равно количеству "лишних" цифр?
Давайте попробуем подтвердить (или опровергнуть) эту гипотезу.
446 0.18548074462379962750
451 0.074462379962749567352
456 0.23799627495673518858
556 0.70277053921717629318
561 0.053921717629317675234
566 0.17176293176752384675
591 0.76694051320005681271
596 0.051320005681271452636
601 0.00056812714526356082773
606 0.81271452635608277858
741 0.47713099605187072113
746 0.099605187072113500000
751 0.51870721134999999837
776 0.49951059731732816096
781 0.059731732816096318595
786 0.17328160963185950245
851 0.71010003137838752887
856 0.0031378387528865875332
861 0.78387528865875332084
991 0.21642019893809525720
996 0.019893809525720106549
1041 0.82303019520353018530
1046 0.01952035301852968995S
1051 0.035301852968995773623
1111 0.45415069595082953312
1116 0.069595082953311686173
1121 0.50829533116861727856
1166 0.19255060400927701671
1171 0.060400927701671139010
1176 0.092770167113900984882
1181 0.016711390098488240129
1266 0.68471040475346462080
1271 0.040475346462080466843
1276 0.53464620804668425907
1331 0.66024058038150193511
1336 0.058038150193511253382
1386 0.92726042699227967824
1391 0.042699227967823547816
1516 0.75596023648066549912
1521 0.023648066549911988183
1551 0.63698074265425278626
1556 0.074265425278625518184
1601 0.81647060016145249192
1606 0.060016145249192173217
1756 0.67179049460165346680
1761 0.049460165346680498863
1766 0.01653466804988627232S
1831 0.95068006422512520512
1836 0.00642251252051173929S5
1856 0.84896084128488626946
1861 0.084128488626945604242
1896 0.11863067442786220392
1901 0.067442786220391949450
1916 0.94945047123713786961
1921 0.047123713786960956364
1966 0.41389086583264599581
1971 0.08658326459958133904S
2021 0.98352595709825822621
2026 0.59570982582262052249
2031 0.98258226205224894077
Итак, все говорит о том, что эта гипотеза верна! А знаете, почему? Потому что ведущие нули не учитываются при подсчете значащих цифр (а ведь именно их количество и равно разрядности). "Ну, это я знал с шестого класса, если не с пеленок. Давайте лучше решим задачу до конца, раз уж мы столь тщательно проверили предложенный мною вариант программы и убедились в его правильности!" — воскликнет иной искушенный читатель. Что же, не возражаю. Давайте зададим параметры и получим результат.
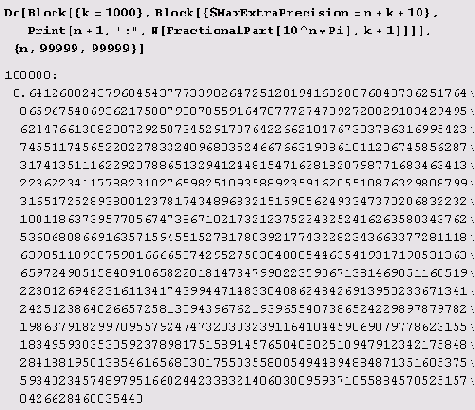
Полужирным здесь выделены искомая сто первая тысяча цифр в представлении числа к десятичной дробью, причем первая выделенная цифра является стотысячной после запятой. "Ну вот, и все дела. Я сразу говорил, что нужно применить функцию FractionalPart. А автор все сомневался, проверял тривиальную программу, сравнивал десятичные знаки с предварительно вычисленными значениями я, измышлял гипотезы... Да в этой программе Pi можно заменить любым числом, в конце концов, я такие программы пишу с пеленок!" — возмутится тут искушенный читатель. Ой, не торопитесь делать такие выводы. В математике (и в программировании, и в компьютерной алгебре) есть великие идеи, но нет мелочей. А что касается вещественных чисел, то они свои ловушки расставляют не только на страницах учебников по теории функций вещественного переменного (чтобы изловить ленивых студентов), но и в вполне респектабельных программах (чтобы в эти ловушки на сей раз угодили "искушенные" читатели и нерадивые пользователи). Вспомните, что мы в ходе проверки подтвердили гипотезу о том, что количество ведущих нулей равно количеству "лишних" цифр. Но ведь мы заранее не знаем, сколько ведущих нулей может встретиться при вычислении дробной части FractionalPart [10^n*Pi], так что заранее ручаться за правильный выбор разрядности мы не могли! Нам просто повезло, что выбранное значение разрядности обеспечило нужную точность! В принципе заранее неизвестно, работает ли наша программа для всех натуральных значений n и k. Указанного нами значения $MaxExtraPrecision = n+k+10 может ведь и не хватить для вычисления k+10 значащих цифр дробной части, если она будет начинаться более, чем с десяти нулей! Если бы в десятичном приближении я встречались сколь угодно длинные последовательности нулей, то для каждого k нашлось бы такое n, что программа с задачей не справилась бы! К счастью для "искушенного" читателя в настоящий момент это неизвестно. Зато даже шестиклассник (во всяком случае, участник районных математических олимпиад) без труда может придумать примеры вещественных чисел, для которых эта программа и ей подобные не работают. Нужно просто выбрать число, в десятичной записи которого встречаются все более длинные последовательности нулей. В качестве примера подойдет число 0.1234567891011121314151617181920..., в котором после десятичной точки выписаны последовательно все натуральные числа. Есть, конечно, и более экзотические примеры, что-нибудь вроде
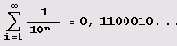
Десятичная запись этого числа содержит только нули и единицы, причем и тех, и других там бесконечно много, но единицы встречаются столь редко, что если наудачу выберешь какую-нибудь цифру, почти наверняка попадешь на последовательность нулей. Так что слухи о том, что придуманная нами программа при тривиальных модификациях может быть применена к любому вещественному числу, были несколько преувеличены...
Да, а как же все-таки решить задачу? Ну, в данном случае это совсем несложно.
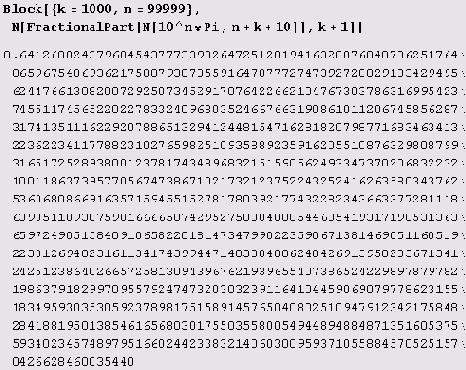
Почему же все-таки я подчеркиваю, что решить задачу несложно именно в данном случае? Вспомните пример с е '"". Там проблема была в том, что вычисленные десятичные приближения заканчивались девятками. А если бы и в этом примере цифры в конце оказались девятками, мы бы не смогли решить, верные ли они. (Именно для того, чтобы избежать округления и убедиться, что последняя цифра не девятка, мы и распечатываем k+1 цифру — k требуемых по условию задачи и одну запасную. Если бы запасная цифра оказалась девяткой, пришлось бы выводить еще несколько запасных цифр, пока не обнаружили бы отличную от 9.) Конечно, мы могли бы увеличить разрядность, но что если бы мы повстречали участок, сплошь состоящий из нескольких миллионов девяток? Может быть, это верные цифры, а может быть, нам просто не хватило точности, и в каком-то миллионе затерялась та единичка в переносе, добавление которой превращает все эти миллионы девяток в миллионы нулей? Вот оно коварство бесконечных десятичных дробей!
Из этого можно извлечь несколько уроков. Во-первых, выполняя действия над вещественными числами, нужно тщательно следить за точностью. Во-вторых, для применения таких функций, как FractionalPart, иногда необходима существенно более высокая разрядность, чем та, которая обеспечивается системой автоматически. В-третьих, иногда перестановка функций позволяет упростить программу. И, наконец, в-четвертых, вещественные числа иногда способны преподносить сюрпризы вроде девяток в конце вычисленных значений или необъятного количества ведущих нулей в начале дробной части. Тогда даже на простые вопросы вроде целое ли это число или конечная ли эта десятичная дробь ответить бывает чрезвычайно трудно. Ведь чем точнее удается приблизить бесконечную дробь рациональными числами, тем больше шансов на то, что она представляет собой число трансцендентное...
Упражнение 3.2 (число Пизо). Вычислите 5555 десятичных цифр числа Пизо
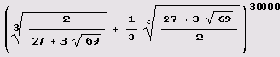
Сколько у этого числа нулей следует сразу после десятичной точки? Решение. Вот самое простое решение. Сначала вводим определение числа.
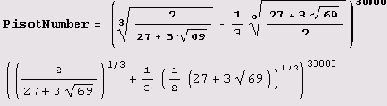
Теперь вычисляем число с указанной точностью.
Ну, как? Не думаете ли вы, что это число заслуживает того, чтобы вычислить его целую и дробную части по отдельности? Сначала вычислим целую часть.
"Ну и что?" — возможно, скажете вы. Тогда присмотритесь внимательнее, где начинаются нули. Да, именно с них и начинается дробная часть.
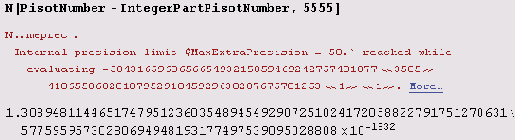
Из этого видно, что после десятичной точки следует 1831 нуль! Чтобы обнаружить, что это число не целое, нужно вычислить его не менее, чем с 5496 десятичными знаками. Вот это можно было бы устроить розыгрыш!
Упражнение 3.3. Пусть
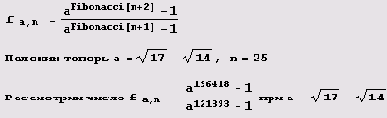
Сколько у этого числа нулей следует сразу после десятичной точки?
Решение. Вот самое простое решение. Сначала вводим определение дроби fajl.
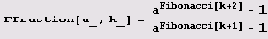
Теперь нужно вычислить число с такой точностью, чтобы найти хотя бы один ненулевой знак после запятой. Давайте попробуем.
N[FFraction[Sqrt[17]-Sqrt[14],25],50]
1.0000000000000000000000000000000000000000000000000
Ну и как? А вот еще:
Хотите еще? Пожалуйста.
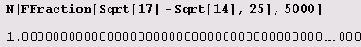
А пятьдесят тысяч знаков после десятичной точки не хотите ли? Хотите. Тогда пожалуйста, только эффект будет в десять раз сильнее.
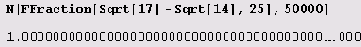
Между прочим, если это число целое, то после десятичной точки у него сплошные нули... И все попытки просто приведут к исчерпанию свободной памяти. Ну бывает же, что дроби сокращаются, а радикалы взаимно уничтожаются:
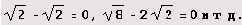
А здесь ведь разность степеней делится на разность степеней... Вот оно, коварство авторов, придумывающих "подленькие" задачи! Возможно, нужно лишь упростить выражение и убедиться, что оно равно какому-нибудь целому числу! Вот если в числителе вычесть и добавить удачно подобранную степень основания:
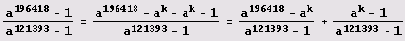
Конечно, сразу же просится k = 121393, тогда сразу же выделится единица:
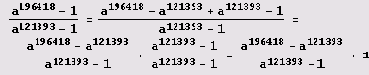
Осталось справиться с числом
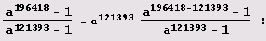
А ведь разность показателей представляет собой разность последовательных чисел Фибоначчи, и потому опять есть число Фибоначчи! Внимательно следите за моей мыслью? Может, надеетесь на дальнейшие упрощения? Так вот они:
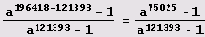
Можно (для удобства исследования) эту дробь обратить и применить к ней тот же прием! И с полученной дробью можно поступить так же! Фактически у нас получатся элементы цепной дроби! После двух десятков (с хвостиком) шагов мы убедимся, что желанного нуля у нас так и не получится. Значит, после десятичной точки все-таки есть цифры, отличные от нуля! Ну вот, а вы говорили о коварстве авторов, придумывающих "подленькие" задачи! Но как же найти эти цифры? Ну, после проделанной работы у вас есть уверенность в наличии таких цифр, и потому вы знаете, что, в конце концов, все время увеличивая точность, вы их найдете. Это важно, ибо вы тем самым убедились в том, что алгоритм, хотя бы теоретически, не зациклится. Но есть и более быстрый способ, ведь мы нашли целую часть и знаем, что дробная не равна нулю. Можем без каких бы то ни было опасений попытаться вычислить логарифм дробной части:
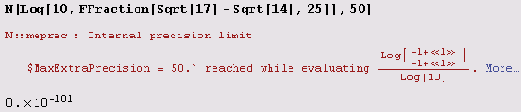
Сразу не получилось... Но можно предпринять и вторую попытку.
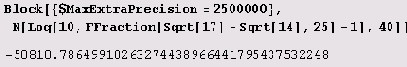
Так, оказывается, после запятой 50810 нулей! Убедимся в этом.
Что касается нулей, то, хоть я и вычеркнул подавляющее их число, предварительно я их посчитал в Word! И их оказалось 50810! Между прочим, убедиться в том, что число fa,n не целое, не так-то просто.
Упражнение 3.4. Пусть
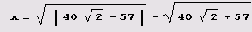
Сколько у этого числа нулей следует сразу после десятичной точки?
Решение. Вот самое простое решение. Сначала вводим определение числа.
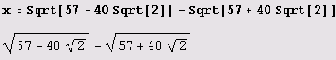
Теперь нужно вычислить число с такой точностью, чтобы найти хотя бы один ненулевой знак после запятой. Итак, попробуем.
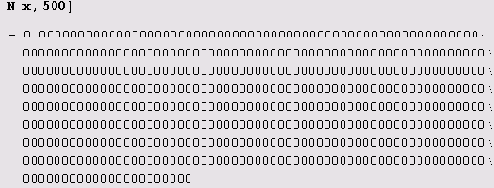
Да это ж предыдущий случай! Мы уже знаем, как с этим справиться.
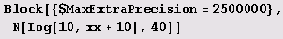
Видите ли... Как бы вам это популярнее объяснить, пока продолжаются вычисления... Отличие от предыдущего случая состоит в том, что в предыдущем случае мы убедились, что 1 действительно является целой частью исследуемого числа. В данном же случае мы лишь предполагаем, что число -10 является целой частью числа х. дН-10 может ведь оказаться и отрицательным, а тогда логарифм окажется комплексным. Это, впрочем, совсем не страшно, мы лишь должны будем вычислить логарифм х+11. Вот и всего-то... Да, но что-то наши вычисления слишком затянулись... Понимаете, тут я должен сделать еще одно разъяснение. Видите ли, чтобы вычислить логарифм, нужно проделать некоторые вычисления, и в нашем случае с довольно высокой точностью. И успех эти вычисления принесут лишь тогда, когда будет обнаружено, что аргумент логарифма (число х+10) отличен от нуля... А в данном случае для этого недостаточно даже вычисления более чем двух с половиной миллионов знаков. Видите ли, бывает же, что дроби сокращаются, а радикалы взаимно уничтожаются. Вот в данном случае как раз х+10 = 0, потому что х= -10. Данное число целое! Давайте попробуем убедиться в этом.
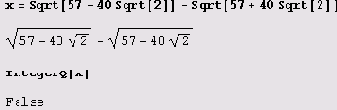
Возможно, вы подумали, что автор хотел обвести вас вокруг пальца! Число все-таки оказалось нецелым! Просто система Mathematica не смогла вычислить достаточное количество знаков, и автор решил упростить себе задачу. Увы, если вы согласились с тем, что число нецелое, совершили довольно распространенную ошибку. Не потому, что оно целое, а потому, что так проверять нельзя. Предикат IntegerQ[x] может принимать значение False даже для целого аргумента. Он проверяет не само число, а его внутреннее представление. Этот предикат принимает значение True только в том случае, если внутреннее представление числа имеет заголовок Integer. Вот как лучше проверять.
Как видите, все ответы тавтологичны. И в данном случае вопрос так и не прояснился... Да, система Mathematica не всегда может то, с чем справляется даже школьник:
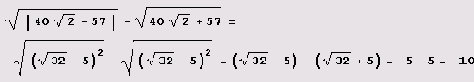
Теперь уж действительно ясно, что число целое. Конечно, придумать таких примеров можно великое множество. И проблема здесь не в коварстве авторов задачников, а в том, что не существует алгоритма (в классическом смысле), который для любого вещественного числа мог бы решить вопрос о том, равно оно нулю или нет. Существует специально разработанный математиками конструктивный анализ, в котором числовой континуум состоит не из обычных вещественных чисел, а из конструктивных. Для конструктивного вещественного числа всегда разрешим вопрос о том, равно ли оно нулю. Конструктивный континуум — та основа, на которой строятся другие объекты конструктивного анализа, например функции. Однако в конструктивном анализе изучаются не любые функции (отображения конструктивного континуума в себя), а только конструктивные. Несмотря на некоторое сходство, свойства конструктивных объектов отличаются подчас радикально.
