Алгебра и пакет Mathematica 5
Число как последовательность (список) цифр
В позиционной системе счисления число фактически представляет собой список цифр. Для получения такого списка и работы с ним в системе Mathematica предусмотрено несколько встроенных функций, наиболее важными из которых являются IntegerDigits, DigitCount, RealDigits и FromDigits.
Представление целого числа в виде списка десятичных цифр: функция IntegerDigits
Разговаривая по телефону, иногда приходится передавать какие-нибудь длинные, например двадцатизначные, числа. В этих случаях обычно читают их цифра за цифрой. Число 587999888735555 читают, например, часто так: пять, восемь, семь, девять, девять, девять, восемь, восемь, восемь, семь, три, пять, пять, пять, пять. В программах тоже иногда нужно по числу определить его цифры. Если вы хотите узнать, является ли шестизначное число счастливым, вам придется сравнить сумму первых трех цифр с суммой последних трех. Поэтому не удивительно, что уже в версии 2 системы Mathematica была предусмотрена функция IntegerDigits, которая представляет число в виде списка цифр. Представим, например, число 25! в виде списка цифр.
IntegerDigits[25!]
{1,5,5,1,1,2,1,0,0,4,3,3,3,0,9,8,5,9,8,4,0,0,0,0,0,0}
Представление целого числа в виде списка цифр в системе счисления с произвольным основанием: функция IntegerDigits
Но, оказывается, функция IntegerDigits может использоваться также для получения списка цифр в системе счисления, основание которой нужно указать вторым параметром. Основание в таком случае может быть любым натуральным числом, большим единицы. Представим, например, число 60! (я полагаю, оно бы очень понравилось шумерам, если бы они его знали) в их любимой шестидесятеричной системе.
IntegerDigits[60! , 60]
{1,20,3,4,48,29,10,11,46,47,21,26,45,46,9,29,47,16,37,50,59,
58,0,33, 59,19,31,10,42,35,8,9,36,0,0,0,0,0,0,0,0,0,0,0,0,0,0}
Иногда нужно представить число в системе счисления не только с заданным основанием, но и с заданным количеством цифр, т.е. дополнить его ведущими нулями в таком количестве, чтобы количество цифр равнялось заданному. Тогда количество цифр в числе нужно задать в качестве третьего параметра функции IntegerDigits.
Вот как число 56 представляется в виде байта.
IntegerDigits[56, 2, 8]
{0,0,1,1,1,0,0,0}
А вот как число 25! записывается в 32-разрядных машинах.
IntegerDigits[25! ,2,32]
{0,1,1,1,1,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0}
Представление целого числа в виде списка цифр в нега-двоичной системе счисления
Если снование системы счисления b является отрицательным целым числом, меньшим -1, то такую систему называют нега-позиционной. Например, если b = -2, то такая система называется нега-двоичной, а если b = -4 — нега-четверичной, если b = - 10 — нега-десятичной. Основным преимуществом этих систем является отсутствие знака перед отрицательными числами и, следовательно, отсутствие правил знаков. Дело в том, что всякое число любой из нега-позиционных систем с четным числом цифр отрицательно, а число, отличное от 0, с нечетным числом цифр — положительно. Особый интерес для конструкторов вычислительных машин представляет, конечно, нега-двоичная система. Однако если задать отрицательное основание (-2) в качестве второго параметра, функция IntegerDiglts "заругается".

Однако функция IntegerDigits позволяет определить функцию, которая сможет представить число в нега-двоичной системе.

И уж совсем просто определить функцию, которая по представлению числа в нега-двоичной системе находит его представление в десятичной системе:

Вот пример (фактически мини-тест) применения обеих функций.

Представление вещественного числа в виде списка десятичных цифр: функция RealDigits
Функция RealDigits позволяет представить вещественное число в виде списка цифр. В этом она похожа на функцию IntegerDigits для целых чисел. Однако, в отличие от функции IntegerDigits, функция RealDigits выдает список, состоящий из двух элементов: списка цифр и количества цифр до десятичной точки.

Представление вещественных чисел в виде списка цифр в системе счисления с произвольным основанием: функция RealDigits
Как и функция IntegerDigits, функция RealDigits может использоваться для получения списка цифр в системе счисления, основание которой нужно указать вторым параметром. Основание в таком случае может быть любым вещественным числом, большим единицы.
RealDigits[617.2857142857142857142857142857,2.5]
{{1,0,0,0,0,1,0,0,1,1,1,2,0,2,0,1,0,0,2,1,0,
1,1,0,0,0,0,0,0,2,1,0,0,2, 0,1,0,2,0,1,0},8}
Однако при вызове функции RealDigits могут возникнуть осложнения в самых тривиальных, на первый взгляд, случаях. Дело в том, что параметры должны быть такими, чтобы по ним функция RealDigits могла определить разрядность представления. Например, первый параметр должен быть вещественным числом, он не может быть записан даже в виде целого числа, если второй параметр задан как Pi.

В этом случае первый параметр нужно задать как 1.0.
RealDigits[1.0,Pi]
{{1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0},!}
Вот еще один пример.
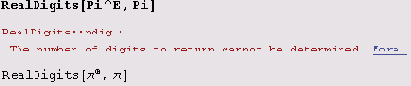
А вот сообщение, совсем "дикое" с точки зрения здравого смысла.

Здесь уж точно можно определить, что нужны только две цифры! Правда, для этого нужно вникнуть в смысл выполняемой операции. Правда, функцию можно обмануть, но лишь с определенной точностью.

Второй способ обмана лучше.

При первом же способе получим следующее.

Здесь Indeterminate — это цифра, в которой функция не уверена.
Представление рациональных чисел в виде списка цифр в системе счисления с произвольным основанием: функция RealDigits
Рациональные числа представляют собой конечные или периодические систематические дроби. Поэтому их представление в виде списка цифр в системе счисления с произвольным основанием имеет некоторые особенности. Проиллюстрируем их на примерах. Пусть имеем рациональное число 99/61. Оно представляется в виде периодической десятичной дроби. Вот как можно вычислить ее начало.
nl= N[99/91,60]
1.08791208791208791208791208791208791208791208791208791208791
Теперь получим список цифр.
n2=RealDigits[N[99/91,60]]
{{1,0,8,7,9,1,2,0,8,7,9,1,2,0,8,7,9,
1,2,0,8,7,9,1,2,0,8,7,9,1,2,0,8,7,
9,1,2,0,8,7,9,1,2,0,8,7,9,1,2,0,8,7,9,1,2,0,8,7,9,1},!}
Пока ничего удивительного. Но ведь список цифр можно получить и проще.
n3=RealDigits[99/91] {{1,{0,8,7,9,1,2}},!}
Оказывается, в этом случае функция RealDigits соображает, что дробь получается периодическая, и находит ее период!
Интересно выполнить обратное преобразование, оно выполняется с помощью функции FromDigits.
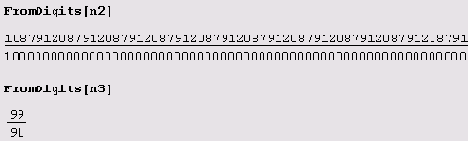
Как видите, если период дроби был выделен явно, обратное преобразование выполняется точно!
Однако период может начинаться не сразу после десятичной точки, как в чисто периодических дробях, а после одной или нескольких цифр. В этом случае количество цифр до периода превышает количество цифр до десятичной точки. Рассмотрим пример.

Как видно из этого примера, других принципиальных отличий нет.
Получение заданного количества цифр вещественного числа в системе счисления с произвольным основанием: функция RealDigits
Мы научились получать список цифр вещественного числа в системе счисления с произвольным основанием. При этом получаются списки цифр определенной длины, которая неявно определяется по параметрам функции RealDigits. Однако количество цифр можно явно указать в качестве третьего параметра функции RealDigits. Вот, например, 300 цифр числа я в системе счисления с основанием е (основание натуральных логарифмов).

Итак, чтобы получить len цифр вещественного числа х в системе счисления с основанием b, вызов функции RealDigits можно записать так: RealDigits [x, b, len]. Если len больше Log [10, b] *Precision[x], то цифры, для которых не хватило точности, представляются как неопределенные (indeterminate).
Получение заданного количества цифр вещественного числа, начиная с цифры определенного разряда в системе счисления с произвольным основанием: функция RealDigits
Если нужно получить len цифр вещественного числа х в системе счисления с основанием 6, начиная с разряда, который в позиционной системе счисления соответствует множителю bn , то вызов функции RealDigits нужно записать так: RealDigits [х, b, len, n]. Например, чтобы вывести только цифры после точки, нужно положить n = -1. Вот еще более "насыщенный" пример.

Однако без дополнительных ухищрений получить вторую после точки тысячу знаков десятичной дроби, приближающей основание натуральных логарифмов, нельзя.

Но даже если увеличить значение $MaxExtraPrecision, все равно ничего не получится (большая часть распечатки пропущена — она заменена троеточием).
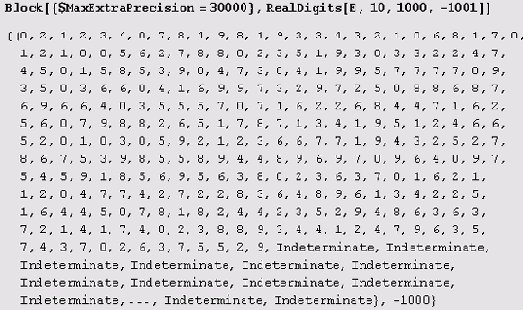
Но не думайте, что эта задача неразрешима, просто функцию RealDigits нужно применить к предварительно вычисленному приближению основания натуральных логарифмов.

Честно говоря, запятых здесь слишком много. Возникает соблазн избавиться от них следующим способом.

Обратите внимание на то, что при этом способе теряются ведущие нули! У нас, например, потерялся один нуль.
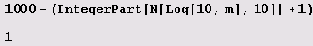
Реконструкция числа по списку цифр, полученному с помощью функций IntegerDigits и RealDigits, — функция FromDigits
Как мы видели, иногда по списку цифр (и других вспомогательных данных) нужно восстановить число. Это выполняется с помощью функции FromDigits. Если этой функции передать один параметр — список, то при восстановлении числа она считает, что цифры в списке — десятичные. Но при необходимости можно указать и основание системы счисления как второй параметр. Вот как, например, можно получить приближение л в виде десятичной дроби, а затем интерпретировать ее как шестнадцатеричную.

Можете ли вы узнать я? Едва ли!
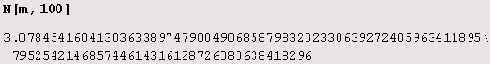
Но на самом деле восстановить его очень просто.
k=RealDigits[m,16]
{{3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,3,8,4,6,2,6,4,3,3,8,3,2,7,9,5,0,2,
8,8,4,1,9,7,1,6,9,3,9,9,3,7,5,1,0,5,8,2,0,9,7,4,9,4,4,5,9,2,3,0,7,8,1,
6,4,0,6,2,8,6,2,0,8,9,9,8,6,2,8,0,3,4,8,2,5,3,4,2,1,1,7,0,6,8},!}
Если первый аргумент имеет вид {список, n}, то n рассматривается как показатель степени (основанием степени служит основание системы счисления), на которую умножается число, восстановленное по списку цифр. Если список имеет вид {список-l, (список-2}}, то список-2 рассматривается в качестве периода систематической дроби.
Функция IntegerDigits теряет знак числа, поэтому FromDigits [IntegerDigits [n] ] равно абсолютной величине Abs [n], а' не n.
"Цифромания": как посчитать девятки в десятичном представлении е — функция DigitCount
Система Mathematica позволяет вычислить столько констант! С точки зрения "цифроманов" было просто преступно не воспользоваться этим и не узнать, например, как распределены единицы и нули в числах От 1 до 256, записанных в двоичной системе, или же не посчитать количество девяток в десятичном представлении основания натуральных логарифмов. Именно для этого (и многих других полезных вещей) как раз и предназначена функция DigitCount. Вызов DigitCount [n, b, d] возвращает количество цифр d (предполагается, что это цифра системы счисления с основанием ь) в числе n, записанном в системе счисления с основанием b. Рассмотрим сначала простой пример. Вот как найти"представление числа 175! в системе счисления с основанием 25.

А вот как можно узнать, сколько раз в этом списке встречается цифра 14
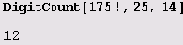
Но это еще что! Можно ведь даже построить график зависимости количества единиц в двоичном представлении n от и.
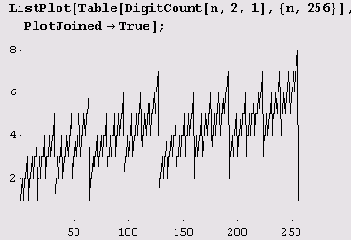
О, это настоящая музыка цифр! Но это еще не все: если третий параметр опущен, функция DigitCount посчитает количество вхождений каждой цифры в представлении числа л в системе счисления с основанием b. (Таким образом, получится список из b чисел.) При этом количество вхождений единицы стоит на 1-м месте в списке, двойки — на 2-м, цифры k (k > 0) — на k-м, а количество вхождений нуля — на последнем, 6-м. Если же опустить и второй параметр — основание системы счисления, то система счисления предполагается десятичной.
Вот как, например, можно сосчитать, сколько раз различные десятичные цифры входят в первые (после запятой) 10 знаков десятичного представления основания натуральных логарифмов.

А вот как узнать, насколько фактически эти цифры отличаются от среднего, 10n.
DigitCount[IntegerPart[10^(10^(n+1))*
FractionalPart[N[E,10^(n+1)+10]]]]-10^n
{1,1,-1,О,-1,-1,0,3,-!,-!}
А теперь посчитаем относительные отклонения от среднего.
N[(DigitCount[IntegerPart[10^(1СГ (n+1))*
FractionalPart[N[E,10^(n+1)+10]]]]-10^n)/10^n,4]
{1.000,1.000,-1.000,0,-1.000,-1.000,0,3.000,-1.000,-1.000}
Ну а теперь мы можем составить таблицу таких отклонений для n = 0, 1, 2, 3, 4, 5.

Одно время некоторых "цифроманов" очень беспокоили неравномерности в распределении девятки в десятичном представлении основания натуральных логарифмов. Честно говоря, просматривая эту таблицу, особых причин для беспокойства именно по поводу девятки я не вижу. Вы имеете возможность просмотреть таблицу, самостоятельно составить более подробную и сформировать собственное мнение — с помощью функции DigitCount это совсем просто! Если же изучать таблицу лень, можно представить данные в виде графика (обратите внимание на то, что ось, на которой отложены значения отклонений, не проходит через начало координат, которое находится вне графика).
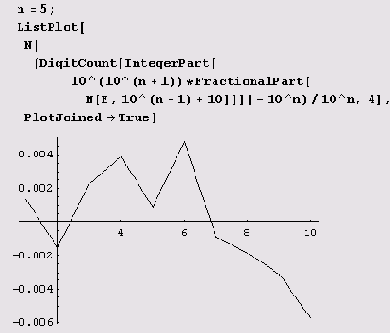
Из графика видно, что наибольшее отклонение от среднего в первом миллионе десятичных знаков не у девятки, а у нуля. Аналогичный график для первых двух миллионов десятичных знаков строится так.
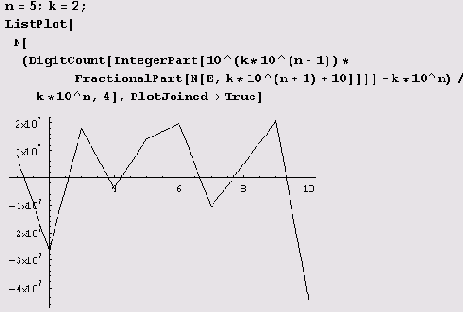
Как видите, если и винить, то скорее нули, а не девятки!
Ну а вот как можно построить график зависимости количества единиц в числе
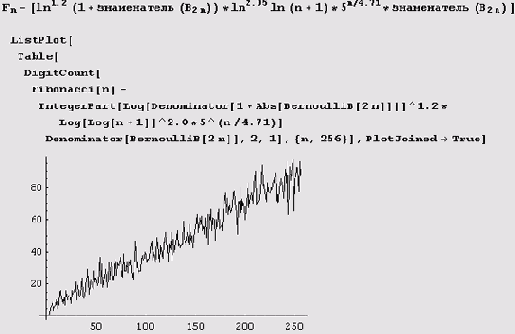
Наконец, можно заняться изучением двоичного представления числа числителъ (В2n) х знаменателъ(В2n). Вот отклонение количества единиц в представлении от среднего.
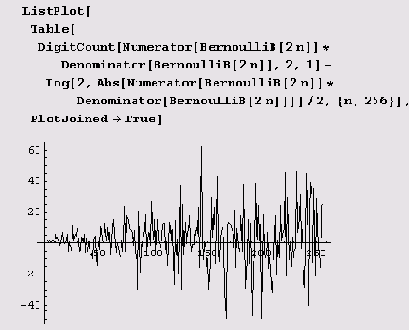
А вот и относительное отклонение.
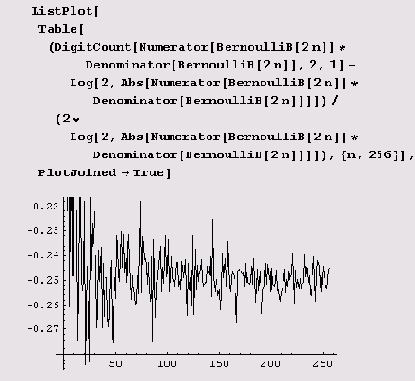
Какие стремительные взлеты и падения!