Представление числа непрерывной дробью: функция Continued Fraction

Функция ContinuedFraction [x] преобразует число д: в непрерывную дробь. Количество звеньев определяется точностью числа х. Следующая программа, например, находит представления первых 50 чисел Бернулли в виде цепных дробей.

Do[

Print[2n,":",ContinuedFraction[BernoulliB[2n]]],{n,0,50} ]

Как видно из таблицы, некоторые числа Бернулли представляются цепной дробью с очень небольшим количеством звеньев.

Количество звеньев цепной дроби можно задать явно в качестве второго параметра.

Это позволяет получить наилучшие приближения числа дробями, знаменатели которых не превосходят некоторого числа. Пусть, например, нужно найти первые 20 звеньев цепной дроби, представляющей число



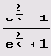
(Разложение этих чисел в цепную дробь при любом натуральном k было найдено Эйлером в 1737 году.) Вот нужная нам программа.

Do[Print[k,":",ContinuedFraction[Е^(2/k), 20]],

{k,1,10}]

Если у цепной дроби количество звеньев меньше заданного, будет сгенерировано предупреждение. Вот как выглядят, например, результаты разложения корней из 2 в цепную дробь с 20-ю звеньями.

Такое предупреждение, как видим, не препятствует работе программы.

Числа Фибоначчи и цепные дроби

Давайте разложим 

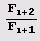
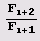
Как видите, количество звеньев разложения дроби  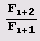  никакая другая дробь такого разложения не имеет.

Вообще, выражения, содержащие числа Фибоначчи, доставляют подчас примеры чисел, разложения которых в цепные дроби обладают весьма интересными свойствами.

Пример 3.2. Давайте определим следующую функцию.

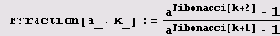
А теперь давайте попытаемся представить несколько ее значений в виде цепных дробей. Положим, например, а = 2, k = 15. Вот результаты.

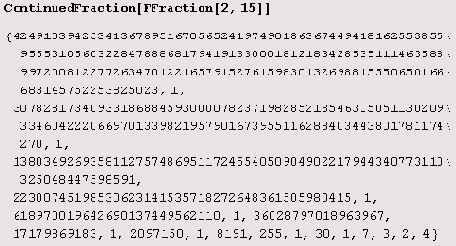
А теперь давайте возьмем логарифмы по основанию 2.

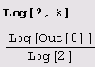
Если и это вам ничего не напоминает, взгляните вот на это.

Table[Fibonacci [n] ,{п,15,2,-1}]

{610,377,233,144,89,55,34,21,13,8,5,3,2,1}

Так что все звенья цепной дроби (кроме последнего), в которую разлагается число 

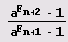
Фибоначчи F_n, F_n-1, F_n-2,,..., F₂, записанные в обратном порядке! То же самое имеем и для а = 3, k = 25.

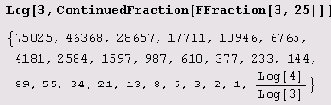
Последний элемент цепной дроби, как видим, равен n+1. Конечно, фокус основан на тождестве

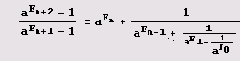
Хотя тождество справедливо для всех я, таких, что a^Fk=1 (k = 0, 1, ..., n+1), именно для целых а правая часть будет "настоящей" цепной дробью.

Здесь целая часть выделена полужирным, а остальные элементы курсивом через один, чтобы их было легче отличить. Видно, как быстро убывают элементы дроби. Но вот если основание а не является целым числом, картина может измениться кардинально. Вот, например, разложение, в котором основание а само является дробью того же вида.

Как видите, если не считать целой части, то все элементы цепной дроби являются весьма небольшими числами. Однако так бывает не всегда. Возьмем, например, основание а = 1/3.

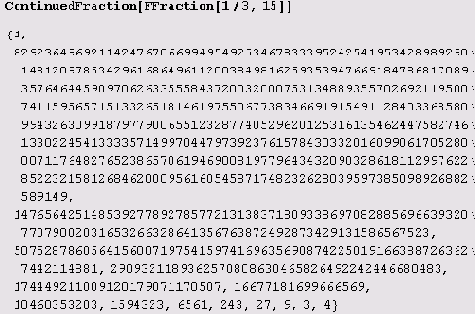
Здесь самым большим является второе звено. Все, кроме него и последнего звена, являются степенями тройки, причем показатели степеней — числа Фибоначчи.

Вот еще пример.

Сколько девяток во втором элементе? 13 = 8+5 = Fibonacci [7] — следующее число Фибоначчи. А сколько нулей? 21 = 13+8 = Fibonacci [8] — опять следующее число Фибоначчи! А сколько цифр во втором элементе? 21 + 13+1 = Fibonacci [9]+l — на единицу больше, чем следующее число Фибоначчи! Но эта единица не для того, чтобы портить картину, она как раз служит для того, чтобы утвердить закономерность, потому что благодаря ей второй элемент равен 10^F9 + 10^F7 -1.

Однако не при всех основаниях картина столь гармонична. Возьмем, например, в качестве основания

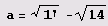
Числа вида

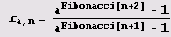
могут доставить множество неприятностей при разложении в цепные дроби. Вот первая попытка получить первые десять элементов разложения в цепную дробь.

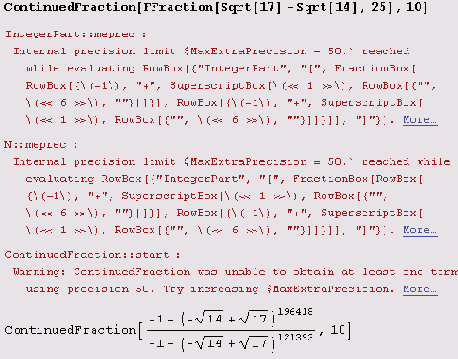
А вот и вторая

Точность — два с половиной миллиона десятичных цифр! Куда ж еще увеличивать?! Давайте разберемся, в чем тут дело.

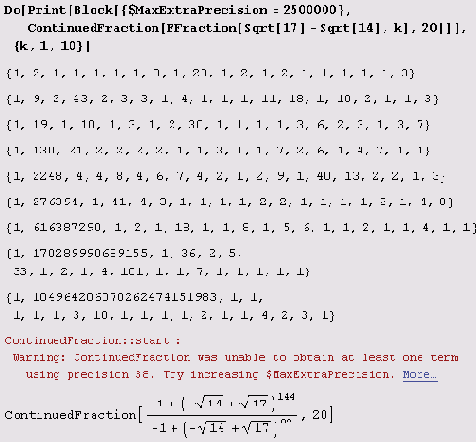
Проблема, похоже, в том, что эти числа слишком быстро приближаются к целому числу 1 с возрастанием п, и потому так быстро возрастает второй элемент. Чтобы сделать картину еще более наглядной, придется прибегнуть к хитрости: увеличим количество вычисляемых элементов. Но чтобы не загромождать распечатку, оставим в ней только 5 элементов. Вот начало распечатки.

Как видите, с ростом n второй элемент возрастает катастрофически быстро, а потому катастрофически быстро возрастает и точность, требуемая для его вычисления.

Периодические цепные дроби

Как доказал Лагранж, все квадратичные иррациональности (и только они) разлагаются в периодические цепные дроби. Как учитывает это обстоятельство система Mathematica? Давайте выясним это на примере разложения квадратных корней из чисел начального отрезка натурального ряда, деленных на 1, 2, 3. Вот определение нужных нам функций.

Fn0l[n_]:=Sqrt[n]

Fn02[n_]:=Sqrt[n]/2

Fn03[n_]:=Sqrt[n]/3

Теперь можем написать программу.

Do[Print[n," : ",

ContinuedFraction[FnOl[n]],":",

ContinuedFraction[Fn02[n]],":",

ContinuedFraction[Fn03[n]] ],{n,1,100}]

Результаты отформатируем в виде таблицы.

Эта таблица заслуживает того, чтобы рассмотреть ее более внимательно. Многие приведенные в таблице квадратичные иррациональности имеют вид 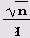² >q. Во-первых, период цепной дроби, представляющей такую квадратичную иррациональность, начинается сразу после целой части. (Это следует из теоремы о чисто периодических цепных дробях, которую Эварист Галуа опубликовал в 1828 году.)

Во-вторых, последний элемент периода равен удвоенной целой части. (Это следует из доказанной Эваристом Галуа теоремы о том, что в случае чисто периодического разложения сопряженная квадратичная иррациональность имеет те же элементы, но расположены они в обратном порядке.)

Наконец, давайте посмотрим, как в системе Mathematica представляются чисто периодические разложения.

ContinuedFractiont(1+13^(1/2))/3]

{1,{1,1,6,1,1}}

Сюрприз! Целая часть, как видите, выделена отдельно, а период записан только со следующего звена! Во многих учебниках по теории чисел считается, что период начинается с первого звена и потому вся дробь записывается в виде {{1,1,1,6,1}}. Конечно, здесь различие только внешнее, но его следует иметь в виду, сравнивая результаты, полученные с помощью системы Mathematica, с результатами, полученными другими системами. Впрочем, при разложении чисел в цепные дроби могут происходить и более серьезные неожиданности...

Частные случаи разложения чисел в цепные дроби

 Очень"иррациональный" случай: 

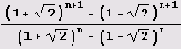
Число 

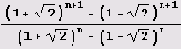
Как видите, ничего не получилось. Система Mathematica говорит, что цепная дробь бесконечна, не имеет периода, и потому советует указать количество необходимых элементов. На самом же деле все эти иррациональности запутали систему Mathematica. Она нуждается в указании упростить выражение. Давайте дадим ей это указание, а заодно и напечатаем числитель и знаменатель нашего очень "иррационального", но на самом деле рационального числа.

Как видите, число оказалось на самом деле рациональным (числители выделены курсивом, а знаменатели — полужирным), а цепная дробь — конечной, но система Mathematica об этом не догадалась. Этот случай говорит о том, что иногда нужно подсказывать, что некоторые выражения можно упрощать. Без этого в данном случае разложение не получить.

Интерес представляют и полученные разложения: все их элементы равны 2, а количество элементов равно п. Никакие другие числа этим свойством не обладают.

Некоторые полезные разложения квадратичных иррациональностей в цепную дробь

В задачниках часто используются разложения в цепную дробь квадратичных иррациональностей вроде

Составим таблицу разложения их в цепные дроби. Сначала определим нужные нам функции.

Fnl[n_]:=  Sqrt[n^2+1]

Fn2[n_]:=  Sqrt[n^2+l]/2 

Fn3[n_]:=  Sqrt[n/42 + l]/n

Вот как выглядит программа для разложения этих иррациональностей.

Do[Print[n,":",

ContinuedFraction[Fnl[n]],":",

ContinuedFraction[Fn2[n]]   ," : ",

ContinuedFraction[Fn3[n]]],{n,1,100} ]

Результаты оформлены в виде таблицы.

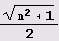
Посмотрите внимательно на третий и четвертый столбцы этой таблицы. Вы увидите нечто весьма интересное:  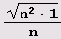  , то несколько удивительно то, что его разложение даже проще: (1, {2n^2,2}}.

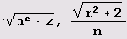
Составим таблицу разложения  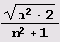  в цепные дроби. Сначала определим нужные нам функции.

Fn1[n_]:= Sqrt[n^2+2]

Fn2[n_]:= Sqrt[n^2+2]/n

Fn3[n_]:= Sqrt[n^2+2]/Sqrt[n^2+1]

После выполнения программы составляем таблицу .

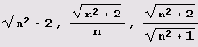
Из таблицы видно, что период всех дробей, являющихся разложением чисел  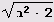, имеет, пожалуй, наиболее сложный период — все его элементы зависят от п. В периодах разложения двух "более сложных" ирра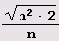циональностей,   лишь первый элемент периода зависит от п. Правда, зависимость эта от n нелинейная, и это как бы "компенсирует" постоянство второго элемента периода. Составим теперь таблицу разложения квадратичных иррациональностей 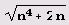 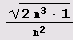  в цепные дроби. Вот определения нужных нам функций.

Fn1[n_]:=  Sqrt[n^4 + 2n]

Fn2[n_]:=  Sqrt[2n^3+1]/2

Программа может быть такой.

Do[Print[n,":",

ContinuedFraction[Fnl[n]],":",

ContinuedFraction[Fn2[n]]],{n,1,100}]

По результатам выполнения программы составляем таблицу. Обратите внимание на третий столбец этой таблицы. Вы увидите, что длина периода некоторых дробей вида 

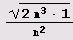
Составим теперь таблицу разложения квадратичных иррациональностей 

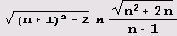
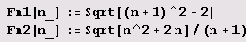
Программу можно не менять; результат выполнения ее представлен в табл. Б.7.

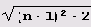
Интересно отметить, что хотя квадратичная иррациональность  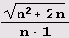  ее период в два раза длиннее.

Более того, в разложении квадратичной иррациональности 

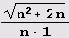
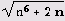
Чтобы составить таблицу разложения квадратичных иррациональностей  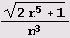  в цепные дроби, нужно дать лишь новые определения нужным нам функциям.

Fnl[n_]:=  Sqrt[rr6+2n]

Fn2[n_]:=  Sqrt[2n^5+l]/(n^3)

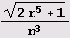
Обратите внимание на то, что у заурядной иррациональности  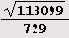  в цепную дробь имеет такой длинный период! Квадратный корень сам по .себе, между прочим, в длине периода не виноват, поскольку период разложения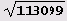 

Составим, наконец, таблицу разложения в цепные дроби квадратичных иррациональностей 

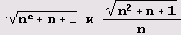
Fnl[n_]:=  Sqrt[nA2+n+l]

Fn2[n_]:=  Sqrt[rr2+n+l]/n

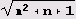
После выполнения программы составляем таблицу . Обратите внимание на второй столбец этой таблицы. Вы увидите, что вполне заурядная иррациональность    отличающаяся всего лишь наличием простенького знаменателя!

Трудные случаи при разложении чисел в цепные дроби

Казалось бы, при разложении чисел в цепные дроби никаких неожиданностей быть не может, поскольку любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Ну а при желании такую дробь всегда можно оборвать, и тогда получится приближение разлагаемого числа с помощью цепной дроби. Но мы уже видели, что не все так просто. Давайте попробуем разложить в цепную дробь число Пизо.

Собственно, не хватило точности. Пока ничего удивительного, даже подсказка есть. Последуем совету.

Сейчас уже $MaxExtraPrecision = 10000000, и потому несколько странно выглядит упоминание о точности 3698. Может быть, система Mathematica вообще не может разложить это число в цепную дробь? Это очень досадно! Не может найти даже 10 звеньев! А если мне нужно узнать, чему равно, например, 1947-е звено? Похоже, ничего поделать нельзя.

Зачем было только увеличивать количество звеньев до 1747, если не удается вычислить ни двух, ни десяти? А за тем, чтобы показать вам сюрприз. Второе звено я выделил курсивом, кое-что опустил (поставил многоточие), но все равно будьте внимательны.

В чем сюрприз? Конечно, не в том, что второе звено содержит 1832 цифры — именно этого мы ожидали, зная, что после запятой следует 1831 нуль. Непостижимо другое: найти 2, 3, ..., 1947 звеньев система Mathematica не может, а вот 1948 (и больше) — может!

Давайте обсудим сложившуюся ситуацию. Оказывается, чтобы найти 2-е, 3-е, ..., 1947-е звено, нужно, как минимум, найти 1948 звеньев, причем нужно догадаться, что если система Mathematica ругается и говорит, что ей что-то не под силу, то задачу нужно сделать более трудной, и только тогда система Mathematica справится с ней в мгновение ока и к тому же без труда!

Я предпочитаю систему Mathematica, поскольку она помогает мне справиться со многими задачами быстрее, чем другие системы компьютерной алгебры. Но должен отметить, что поведение ее в данном случае интуитивно непонятно, и учесть такую возможность в программе весьма непросто. Конечно, система Mathematica — пример системы с искусственным интеллектом, а поведение таких систем предсказуемо далеко не всегда, как и поведение человека. Иногда ведь и человек может справиться с очень трудной задачей, но не может найти ключ к решению более простой задачи. Тем не менее в данном случае от компьютера хотелось бы более детерминированного результата.

Ну и еще один вопрос: это исключение, не так ли? Можете считать, что да. (Сам поступаю очень часто именно так.) Но тогда приходится признать, что таких исключений очень много. Например, добавляя к числу Пизо целые числа, вы получите серию (теоретически бесконечную) новых исключений. Если вы считаете, что такие исключения связаны с кубическими корнями из числа три, то я вас разочарую. Вот число, которое с виду в несколько раз проще, но в десятки (а может, сотни или тысячи) раз "подлее" с точки зрения функции ContinuedFraction.

х=1000!+(Sqrt[2]-1)^10000

Система Mathematica не сможет превратить его в цепную дробь, если вы укажете менее 3667 необходимых звеньев. А если все же указать 3667 звеньев, то тут как раз и окажется, что она может вычислить всего лишь 2613 из заданных 3667.

Далее система Mathematica честно выпишет обещанные 2613 звеньев, причем на первом месте, конечно, будет записано десятичное представление 1000!.. Может быть, все дело в факториале — 1000!? Нет, то же самое происходит и с числом 1 + (√2 -1)¹⁰⁰⁰⁰. Но ведь это квадратичные иррациональности, и цепные дроби должны  быть периодическими! Может, просто не нужно указывать период и получить точное представление? Так и поступим.

Система Mathematica справилась! Она может обнаружить, что цепная дробь периодическая, и правильно определяет ее период. Он, кстати, оказался очень коротким: всего лишь два звена! Так что не составило бы труда выписать и десятки тысяч звеньев, ведь для этого необходимо только достаточное число раз повторить период. Но до этого может догадаться пока лишь человек. Я же надеюсь, что в следующей версии сможет это и система Mathematica! Давайте теперь рассмотрим саму цепную дробь. (Недаром же я привожу ее в книге.) Оказывается, здесь тоже есть неожиданности. Во-первых, первое звено цепной дроби равно 2, хотя целая часть числа равна 1.

Это указывает на то, что в системе Mathematica первое звено цепной дроби не всегда равно целой части числа, даже если число положительно. Во-вторых, оба звена в периоде отрицательны. Все это может усложнить восприятие числа и никоим образом не одобряется авторами учебников и задачников по теории чисел. Такое представление не является стандартным, и потому будьте внимательны. А вот пример стандартного представления:

А вот и еще один пример. Попытаемся разложить целое число 40= Sgrt[57-40Sqrt[2]]-Sqrt[57+40Sqrt[2]] В цепную дробь.

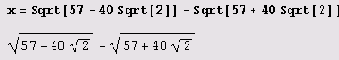
Результат вообще абсурдный:

Заметьте, утверждается, что дробь не является ни конечной, ни периодической! Против отсутствия периода я бы не спорил, но звеньев-то всего одно! Если же указать фактическое количество звеньев, результат получить все равно не удастся.

Фокус с увеличением количества звеньев (например, до миллиона) здесь не проходит, поскольку трудности возникают уже при вычислении целой части, т.е. первого звена.

Мы разобрали всего лишь несколько примеров, где поведение системы Mathematica, мягко скажем, слабо предсказуемо. Но, надеюсь, вы понимаете, что аналогичное произойдет и в случае чисел вида 

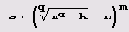
целых 5, k, n, q, удовлетворяющих неравенствам 1<k<n. Конечно, наверняка можно придумать и другие формулы, доставляющие "плохие" числа. Если все это исключения, то не слишком ли их много?! После всего сказанного, возможно, вы даже подозреваете, что неприятности будут вообще в случае чисел вида 1 +е при очень малых е, например при ε= 1/(1000!). Так вот она, непредсказуемость: при ε= 1/(10000!) все происходит без каких-либо неожиданностей. И вообще, при рациональных е неприятностей не бывает. Недаром рациональный значит "разумный"! И уж если мы заговорили о разумном и рациональном, то не разумно ли было бы научиться рациональным способам проверки правильности полученных разложений в цепную дробь? Для этого нужно всего лишь научиться (с помощью системы Mathematica) находить числа по их представлению в виде цепных дробей. Оказывается, это совсем несложно, и именно к этому мы сейчас и перейдем.

Содержание раздела

---

---