Алгебра и пакет Mathematica 5
Факторизация факториалов
Факториалы являются классическим примером больших чисел. В школе, примерно класса с шестого, учителя плавно готовят детей к тому, что факториалы очень быстро растут, а при изучении комбинаторики говорят, что уже 8! = 40320. Тех же, кто этого не устрашится, на школьном кружке пугают тем, что 100! — невообразимо большое число. Такое большое, что даже вычислить его немыслимо. (Но члены школьного математического кружка обычно знают, что это число вычислил Мольтерер еще до появления ЭВМ.) Дня тех же, кто не убоялся этого числа и (зачастую вопреки устрашениям учителей) преодолел конкурсный отбор в вузы, у профессоров есть очередная страшилка: 1000!. Что-то я не видел профессора, который бы выписал десятичную запись этого числа на доске! Наверное, для профессоров оно и вправду страшное! Но не для нас. Мы его (вместе с системой Mathematica) выпишем раньше, чем профессор успеет моргнуть оком.

Действительно, число огромное! Правда, факторизовать его совсем несложно, так как его простые делители известны: даже пятиклассник без труда сообразит, что ими будут все простые числа, меньшие
n = 1000. Что же касается определения показателей, с которыми они входят в каноническое разложение, то здесь положение более сложное. Обычно пятикласснику (участнику городской или районной олимпиады по математике) нужно от пяти до десяти минут на вывод и проверку необходимой формулы. Но ведь Mathematica (точнее, функция
FactorInteger) не проверяет, является ли каждое предлагаемое ей число факториалом некоторого другого числа, и потому применить формулу не сможет! Так сколько же ей понадобится времени на факторизацию этого монстра? На самом деле ответ получается в мгновение ока.
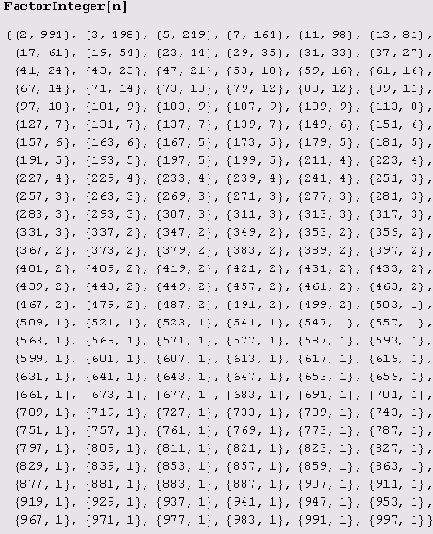
Почему же тогда это разложение получается так быстро? Тому есть две причины. Во-первых, функция Factorlnteger реализует довольно хитрый алгоритм (и к тому же усовершенствованный в версии 5), который умеет пользоваться особенностями числа и ранее найденными множителями. Во-вторых, число имеет малые простые делители, притом в достаточно больших степенях (взгляните на разложение и убедитесь в этом самостоятельно). Поэтому уже в самом начале, как только найден очередной небольшой простой делитель, число делится на его достаточно большую степень, и поиск следующего делителя выполняется для уже значительно меньшего числа. Например, когда найдены все простые делители, меньшие 500, остается факторизовать число
15691 53857 18474 74009 83807 62903 18629
41145 72096 17012 19604 99858
85055 99420 28601 60316 94401 22137 22852
86216 37326 13501 59916 38173
00885 96291 76502 03413 58819 32577 52694 92805
54593 08494 87900 72440 14847 75831
74209 25608 64073 74119.
А ведь это число существенно меньше первоначального. К тому же его простые делители также являются последовательными простыми числами. И потому, хотя уже и не так стремительно, но подлежащее факторизации число все время уменьшается. А это значит, что не приходится испытывать числа, большие 1000. Добавьте сюда еще одну техническую деталь: работать приходится с все более короткими числами, и вы поймете, почему процесс заканчивается столь быстро.
Но есть огромное множество гораздо меньших чисел (вроде 1001-1, (1079-1)/9 и т.д.), которым повезло гораздо меньше. Быстро разложить их функция Factorlnteger не может. Как же быть?