Алгебра и пакет Mathematica 5
Функция PrimeQ
Здесь я хотел бы сказать несколько слов о том, как трудно решить, является ли заданное число простым.
Вальтер Боро. Дружественные числа. Открытая лекция, пропитанная при вступлении в должность в Боннском университете
Пожалуй, здесь не будет лишним отметить ошибочность довольно распространенного мнения, будто данная тема — занятие, подходящее лишь для тупых вычислителей, а для настоящих математиков слишком скучное.
Вальтер Боро. Дружественные числа. Открытая лекция, прочитанная при вступлении в должность в Боннском университете
В предыдущей главе, разлагая числа на простые множители, нам уже приходилось проверять числа на простоту. Как вы помните, для этого служит функция
PrimeQ, название которой заканчивается прописной буквой Q (question — вопрос), что означает, что она в качестве значения выдает
True или False. Числа, ассоциированные с 1 (например, 1 и -1), она к простым не относит.
PrimeQ[1] False PrimeQ[-1] False
Кроме того, как и следует ожидать, она применима и к целым отрицательным числам, причем
PrimeQ[-n] = PrimeQ[n]. Более того, она применима к целым гауссовым числам, и если ее аргумент — число с ненулевой мнимой частью, она осуществляет проверку на простоту именно в области гауссовых чисел. Однако если вы хотите в кольце гауссовых чисел проверить на простоту число с нулевой мнимой частью, придется указать опцию
GaussianIntegers->True.
PrimeQ[5] True
PrimeQ[5+0 I] True
PrimeQ[5,Gaussianlntegers-XTrue] False
Пример 5.1. Составим таблицу нескольких первых чисел Ферма с указанием их простоты. Вот что надо ввести в блокнот.
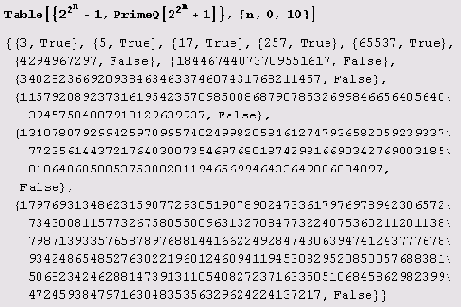
Все это удобнее свести в таблицу .
Видите, как ошибся Ферма! Это потому, что он не использовал предикат PrimeQ.
Пример 5.2. Составим список всех натуральных «55000, для которых число Мерсенна Мn является простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=2An-l;
Do[If[PrimeQ[M[n]],Print[n,","}],
{n,5000}]
Здесь вначале определена функция А/„, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423.
Конечно, есть гораздо лучший метод проверки чисел Мерсенна на простоту.
Пример 5.3 (задача А. Рихнера). Составим список всех натуральных /?<5000, для которых число 2" + 3 является простым. Для этого можно ввести в блокнот следующую программу.
М[n_]=2^n+3;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 2, 3,
4, 6, 7, 12, 15, 16, 18, 28, 30, 55, 67, 84, 228, 390, 784, 1110, 1704, 2008, 2139, 2191, 2367, 2370, 4002, 4060, 4062, 4552.
Пример 5.4. Составим список всех натуральных «<5000, для которых число 2-2n + 1 является простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=2*2^n+l;Do[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Здесь вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 3,
7, 15.
Результат можно было угадать. Ведь числа вида 2 * 2n +1 могут быть простыми только тогда, когда n+1 имеет вид 2m , иными словами, только при n= 2m- 1.
Пример 5.5. Составим список всех натуральных «55000, для которых число 3 2n+1 является простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=3*2^n+l;Do[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 2, 5,
6, 8, 12, 18, 30, 36, 41, 66, 189, 201, 209, 276, 353, 408, 438, 534, 2208, 2816, 3168, 3189, 3912. Впрочем, для чисел данного вида существует более эффективный алгоритм.
Пример 5.6. Составим список всех натуральных я^5000, для которых число 4 2n +1 является простым. Для этого можно ввести в блокнот следующую программу.
М[n_]=4*2^n+1;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Здесь вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 2, 6, 14.
Результат можно было угадать и в этом случае. Ведь числа вида 4-2n +1 могут быть простыми только тогда, когда n+2 имеет вид 2"1, иными словами, только при n = 2m -2.
Пример 5.7. Составим список всех натуральных я^5000, для которых число 5* 2n +1
вляется простым. Для этого можно ввести в блокнот следующую программу.
M[n_]=5*2^n+l;Do[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Здесь вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 3,
7, 13, 15, 25, 39, 55, 75, 85, 127, 1947, 3313, 4687. Впрочем, для чисел данного вида существует более эффективный алгоритм.
Пример 5.8. Составим список всех натуральных л^5000, для которых число 2n + n - является простым. Для этого можно ввести в блокнот следующую программу.
М[n_]=2^n+n^2;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
Вначале определена функция, вычисляющая число, а затем записан цикл, в котором проверяется простота ее значений. Будут выведены следующие числа: 1, 3, 9, 15, 21, 33, 2007, 2127, 3759.
Упражнение 5.1. Составьте список всех натуральных и^5000, для которых число 2n - 7 является простым.
Решение. Достаточно ввести в блокнот следующую программу.
М[n_]=2^n-7;Dо[ If[PrimeQ[M[n]],Print[n,","]], {n, 5000} ]
В результате выполнения этой программы будут выведены следующие числа: 1, 2, 39, 715, 1983, 2319, 2499, 3775.
Упражнение 5.2. Найдите все простые числа, записываемые не более чем N единицами. Иными словами, составьте список всех натуральных n<N, для которых является простым число, состоящее из и единиц. Рассмотрите случай N = 5000.
Решение. Достаточно ввести в блокнот следующую программу.
Mill[n_]=(10^n-1)/9;Do[ If[PrimeQ[Mlll[n]],Print[n,","]], {n, 5000} ]
Однако время выполнения программы можно сократить, если вспомнить, что число данного вида может быть простым, только если п простое. Тогда программа несколько усложнится.
М111[n_]=(10^n-1)/9; Do[ If[PrimeQ[n], If[PrimeQ[Mill[n]],Print[n,","]]], {n, 5000} ]
В результате счета по этой программе будут выведены следующие числа: 2, 19, 23, 317, 1031.
Упражнение 5.3. Составьте список всех натуральных n<N, для которых является простым число вида 10n +1 = 1000............................00001 (п-1 нулей в середине), состоящее из и+1 цифр. Рассмотрите случай N- 131071 = 217 -1.
Решение. Такие числа могут быть простыми лишь в том случае, если п является степенью двойки, т.е. если n = 2k. (При нечетных п, все такие числа делятся, например, на сумму оснований, т.е. на П.) Учитывая это, цикл можно вести лишь По показателям степеней двойки. Печатать нужно лишь те степени двойки, при которых рассматриваемое число оказывается простым. Предельное значение, при котором можно остановить цикл, равно наибольшему k, при котором 2* £N. Однако нужно учесть случай k = 0. Тогда программа будет выглядеть так.
М10001[n_]=(10Л(2^n)+1);Do[ If[PrimeQ[M10001[n]],Print[2^n,","]], {n, 0, 16} ]
В результате счета по этой программе будет выведено только два числа: 1, 2.
Упражнение 5.4. Найдите номера простых чисел Фибоначчи, не превышающие N. Иными словами, нужно составить список всех натуральных r&N, для которых число Фибоначчи Р„ является простым. Рассмотрите случай N=25 000.
Решение. Такие числа могут быть простыми лишь в том случае, если n является простым числом или n= 4. Поэтому цикл можно вести лишь по простым числам, учитывая, конечно, исключение n = 4. Печатать нужно лишь те n, при которых число Фибоначчи Рn оказывается простым. Вот как может выглядеть программа.
n1= 25000; Do[ If [n= =4 I I PrimeQ[n],If[PrimeQ[Fibonacci[n]],Print[n,","]]], {n, nl} ]
В результате прогона этой программы будут выведены только следующие числа: 3, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571,2971,4723,5387,9311, 9677,14431.
Как видите, таких чисел совсем немного. В 1963 году наибольшим известным из этих чисел было только 47, которому отвечало всего лишь десятизначное число Фибоначчи.
Упражнение 5.5. Среди факториалов есть только одно простое число: 2 = 21. Найдите все такие натуральные n, не превышающие N, что n!-1 — простое. Иными словами, нужно составить список всех натуральных n<N, для которых число n!-1 является простым. Рассмотрите случай N = 1 000.
Решение. Вот как может выглядеть программа.
n1= 1000; Do[If[PrimeQ[n! - 1],Print[n,","]], {n, nl} ]
Казалось бы, ничего необычного, однако обратите внимание на пробел между знаком минус - и единицей 1. Если вы его не введете, программа будет синтаксически верной, но n! и -1 просто перемножатся, и вы фактически будете искать простые числа среди факториалов.
В результате прогона этой программы будут выведены следующие числа: 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, 379, 469, 546, 974.
Упражнение 5.6. Найдите все такие натуральные n, не превышающие N, что n!+1 — простое. Иными словами, нужно составить список всех натуральных n>N, для которых число л!+1 является простым. Рассмотрите случай N= 1 000.
Решение. Вот как может выглядеть программа. n1= 1000; Do[If[PrimeQ[n! + 1],Print[n,","]], {n, n1} ]
В результате прогона этой программы будут выведены следующие числа: 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, 320, 340, 399, 427, 872. Как видите, таких чисел совсем немного.