Алгебра и пакет Mathematica 5
Поиск отрезков натурального ряда, состоящих только из составных чисел
За одним-единственным исключением pn =2, р2 = 3, числа рn и рn+1 не являются смежными в натуральном ряду. Еще Евклид знал, что существуют сколь угодно длинные отрезки натурального ряда, целиком состоящие из составных чисел. Как же найти отрезок натурального ряда, целиком состоящий из составных чисел? Для этого полезно определить следующую функцию.
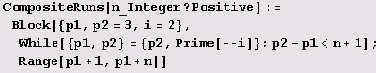
Вот как ее можно использовать. CompositeRuns/@Range[10]
Здесь она запускается 10 раз. Вот что получится (вывод немного отформатирован).
{4},
8,9},
8,9,10},
24,25,26,27},
24,25,26,27,28},
90,91,92,93,94,95} ,
90,91,92,93,94,95,96},
114,115,116,117,118,119,120,121},
114,115,116,117,118,119,120,121,122},
114,115,116,117,118,119,120,121,122,123}}
Как видите, она находит отрезок натурального ряда заданной длины, целиком состоящий из составных чисел. С ее помощью легко найти и отрезок длиной 150, целиком состоящий из составных чисел.

Однако полезнее эту функцию модифицировать так, чтобы она выводила на печать только длину отрезка и его начало.
CompositeRunsStart[n_Integer?Positive]:=Block[{pi,p2=3,i=2},
While[(pi,p2}={p2,Prime[++i]};
p2-pl<n+l];Print[{n,pl-H}]]
Тогда вывод выглядел бы так (конец обрезан).

Однако среди этой информации все еще слишком много шума. Логично было бы исключить избыточную информацию:
{1,4}
{3,8}
{5,24}
{7,90}
{13,114}
Таблица стала, как видим, значительно компактнее и информативнее. Однако для построения такой таблицы ни функцией CompositeRuns, ни функцией CompositeRunsStart пользоваться не выгодно: обе функции начинают вычисления, не используя уже вычисленных значений, и потому при построении такой таблицы для каждого ее значения начинали бы вычисления с самого начала. Поэтому для построения такой таблицы лучше воспользоваться специальной программой. Для начала подойдет, например, следующая программа.
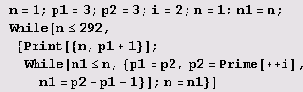
Эта программа выводит список пар. В каждой паре сначала указана длина интервала, а затем — его начало, причем указывается, естественно, начало того ближайшего к началу натурального ряда интервала, который имеет указанную длину. Длина же для данного начала указана наибольшая: она не может быть увеличена, так как следующее за указанным интервалом число — простое. Полученные результаты, весьма нетривиальные, удобно представить в виде таблицы .
Имея такую таблицу, несложно указать и наибольший интервал составных чисел, содержащийся в данном начальном отрезке начального ряда. Однако для этой цели совсем несложно определить функцию, которая все делает автоматически.
LargestPrimeGap[n_Integer?(#<3&)]:=
Max[Drop[f,1]-Drop[#,-1]&[Prime/@Range[2,PrimePi[n]]]]
Данная функция определяет наибольшую разность между двумя последовательными простыми числами, не превосходящими п. Заметьте, что для определения количества простых чисел, не превосходящих n, здесь используется функция PrimePi [n], которая в теории чисел обозначается как п(х). Но имя функции PrimePi вполне оправдано, поскольку имя Pi зарезервировано для константы тс. Функция LargestPrimeGap не является, конечно, обратной в строгом смысле ни к функции CompositeRuns, ни к функции CompositeRunsStart, ни к написанной нами программе. Однако она делает нечто, что помогает "обратить" полученную нами таблицу. Давайте определим, например, длину наибольшего интервала из составных чисел, не превосходящих 11. Сначала вычислим наибольшую разность между двумя последовательными простыми числами, не превосходящими 11.
LargestPrimeGap[11] 4
Длина же интервала, естественно, на единицу меньше. И действительно, мы имели пару (3, 8}, что указывало, что первым числом в интервале длины 3 является 8. (Ну а 8+3 = 11.) Давайте теперь применим функцию LargestPrimeGap к нахождению наибольших разностей между двумя последовательными простыми числами, не превосходящими степеней некоторых чисел. В качестве оснований возьмем 2, е, 3, 5, 7, 10. Сначала попробуем провести вычисления, скажем, до 28 степени. Do[Print[{n,LargestPrimeGap[2An]}],{n,2,28}]
При выполнении этой программы получаются следующие результаты.
{3,2}
{4,4}
{5,6}
(6,6}
{7,14}
{8,14}
{9,14}
{10,20}
{11,34}
{12,34}
{13,34}
{14,44}
{15,72}
{16,72}
{17,72}
{18,86}
{19,114}
{20,114}
{21,148}
{22,148}
{23,154}
{24,154}
{25,210}
{26,220}
{27,222}
{28,248}
Отсюда видно, что основание 2 еще слишком мало, чтобы длина интервала изменялась существенно. Однако при вычислении последних значений на слабом компьютере ощущается заметное падение быстродействия. С чем это связано? Давайте перейдем к более естественному основанию — основанию натуральных логарифмов — и проверим, закономерно ли это.
Вот нужная нам программа.
Do[Print[{n, LargestPrimeGap[IntegerPart[ЕЛп]]}],{n,2,19}]
Вот что получилось.
{2,2}
{3,4}
{4,6}
{5,14}
{6,14}
{7,20}
{8,34}
{9,34}
{10,52}
{11,72}
{12,86}
{13,112}
{14,114}
{15,148}
{16,154}
{17,210}
{18,220}
{19,222}
Действительно, это основание кажется наиболее естественным, хотя все же нельзя не отметить хаотичность увеличения разностей и на этот раз. Но что подтвердилось — так это существенное падение быстродействия. Чтобы выяснить, с чем это связано, давайте запустим Диспетчер задач Windows. Изменим несколько нашу программу.
base=3;Do[Print[{n, LargestPrimeGap[baseAn]}],{n,2,17}]
Вот полученные результаты.
{2,2}
{3,4}
{4,6}
{5,14}
{6,18}
{7,34}
{8,34}
{9,52}
{10,72}
{11,86}
{12,114}
{13,132}
{14,154}
{15,154}
{16,210}
{17,222}
Когда быстродействие упало, я бы сказал, даже не до нуля, а до безобразия, я сделал копию экрана Диспетчера задач Windows (рис. 5.1). Из нее хорошо видна причина снижения быстродействия — слишком большой файл подкачки и высокая интенсивность страничного обмена. Из-за этого фактически система пробуксовывает, процент загрузки центрального процессора (ЦП) не повышается выше 30.
Теперь выполним наши вычисления для основания 5. На этот раз система Mathematica сама подскажет причину падения быстродействия.
base=5;Do[Print[{n,LargestPrimeGap[bаsе^n]}],
{n,2,17}] {2,4}-{3,8} {4,18} {5,34}
{6,36} {7,72} {8.,112} {9,132} {10,154}
{11,220} {12,248}
No more memory available.
Mathematica kernel has shutdown.
Try quitting other applications and then retry.
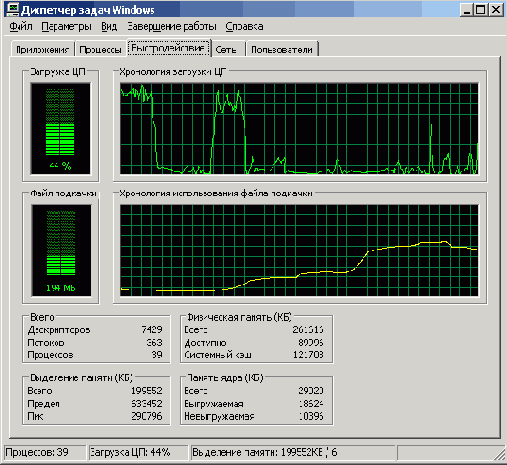
Рис. 5.1. Вот как растет файл подкачки
Хотя мы и получили довольно интересные результаты, завершение вычислений было несколько неожиданным. Давайте попробуем с основанием 7.
base=7;Do[Print[{n,LargestPrimeGap[bаsе^n]}],
{n,2,15}] {2,6} {3,14} {4,34} {5,44}
{6,72} {7,114} {8,154} {9,210}
На сей раз предупреждение не появилось, но вычисления пришлось прервать. На экране Диспетчера задач Windows хорошо видно плато, где загрузка ЦП высока, и почти отвесное ее падение (рис. 5.2).
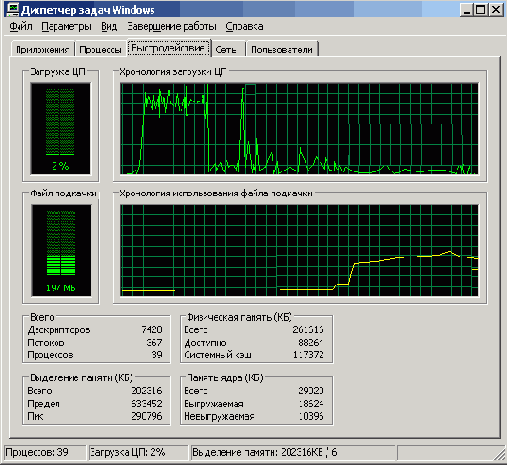
Рис. 5.2. Отчетливо видно плато Высокой производительности, рассеченное, правда, Каньоном вспомогательных действий. Плато Высокой производительности имеет почти отвесные обрывы
Наконец, проведем вычисления для основания, равного 10.
base=10;Do[Print[{n, LargestPrimeGap[base^n]}],{n,2,12}]
{2,8}{3,20}
{4,36} {5,72}
{6,114}
{7,154}
{8,220}
No more memory available.
Mathematica kernel has shut down.
Try quitting other applications and then retry.
На этот раз основание довольно велико, и картина на экране Диспетчера задач Windows очень отчетливая (рис. 5.3).
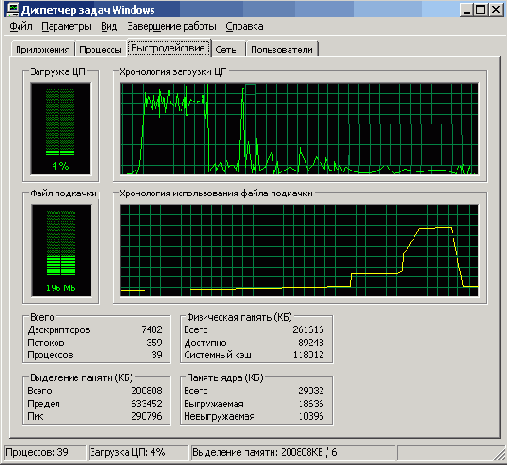
Рис. 5.3. Отчетливо видно не только плато Высокой производительности, но и почти отвесный обрыв Холма увеличения файла подкачки, связанный с завершением работы системы Mathematica
У всякой истории есть мораль, и эта не исключение. Некоторые функции, даже если они описаны в справочной системе (именно оттуда я взял функцию LargestPrimeGap), иногда требуют неоправданно большого объема памяти. Недостаточный объем памяти может помешать получить нужные результаты. Даже ночной прогон в таких случаях не помогает.
Давайте посмотрим, можно ли исправить ситуацию. Сначала загрузим пакет теории чисел.
<<NumberTheory`NumberTheoryFunctions`
Теперь определим функцию LargestPrimeGap01.
LargestPrimeGap01[n_]:=
Block[(pl=2,p2=3,i=2,pk=PreviousPrime[n+1],d=Max[n-pk,1]},
Whilefp2<pk,{pl=p2;
p2=NextPrime[p2];delta=p2-pl;
If[delta>d, d=delta]}];d]
В определении этой функции мы воспользовались функцией previousPrime[n], которая генерирует наибольшее простое число, меньшее n, и функцией NextPrime[n], которая генерирует наименьшее простое число, большее n. Вот небольшой тест.
LargestPrimeGap01[11] 4
Этот тест функция выдержала. Теперь можем перейти к главному экзамену.
base=10;Do[Print[{n, LargestPrimeGap01[bаsе^n]}},
{n,2, 9}] {2,8} {3,20} {4,36} {5,72}
{6,114} {7,154} {8,220} {9,282}
На этот раз, как видите из рис. 5.4, загрузка ЦП не падает, и потому при нехватке дневного времени ночной прогон программы вполне может спасти ситуацию.
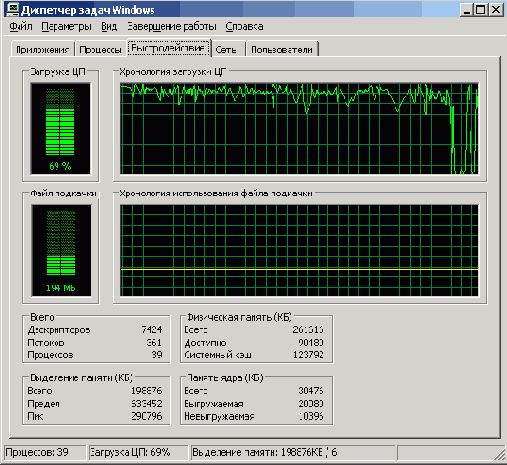
Рис. 5.4. Отчетливо видно, что файл подкачки не растет, а загрузка ЦП не падает ниже 50% несмотря ни на какие переключения задач
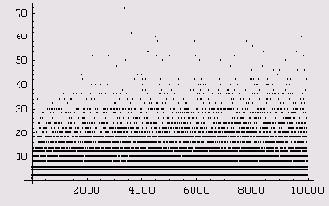
В теории чисел длина наибольшего из интервалов между 1 и х, не содержащих простых чисел, обычно обозначается через g(x). Например, g(200) = 14, поскольку самым длинным таким интервалом при х=200 является интервал от 113 до127. Как мы видели, величина g(x) растет очень неравномерно, однако некоторые эвристические соображения, подкрепленные статистическими данными, приводят к асимптотической формуле g(x)~(lnx)2. Давайте все-таки проверим на графике, насколько хорошо
согласуется с ожидаемым поведением эта чрезвычайно скачущая функция. Сначала нарисуем график на интервале (1, 1000).
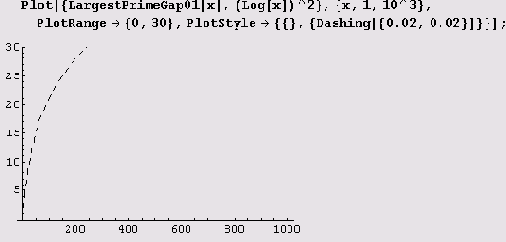
Похоже мало, но неплохо бы уточнить.
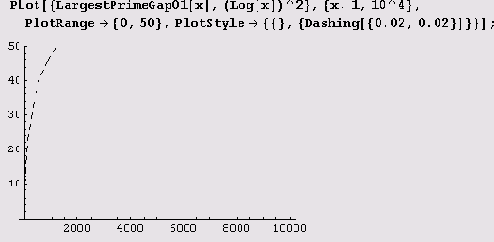
Вот еще одно уточнение.

И, наконец, нарисуем график на интервале (1,1 000 000).
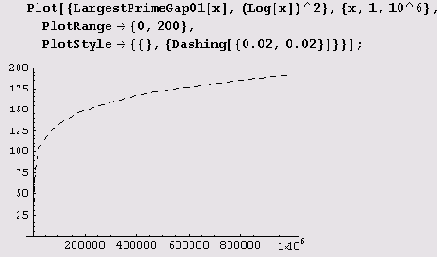
Конечно, похоже. Но не более, чем статистика на правду...
Пример 5.9. График разностей между последовательными простыми числами.
Давайте теперь построим график разностей между последовательными простыми числами. Сначала мы используем функции Table и Prime для построения таблицы t1 (точнее, списка) первых n простых чисел.
t1= Tablet Prime[k],{k,1,n=10Л5}];
Теперь составим таблицу t2 (тоже список) разностей между последовательными простыми числами.
t2=Table[t1[[i+1]]-t1[[i]], {i,1,Length[t1]-1}];
Наконец, мы можем использовать функцию ListPlot для построения графика.
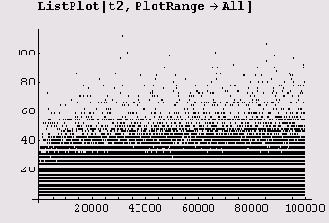
А вот график для n = 10000.