Алгебра и пакет Mathematica 5
Простые числа, близкие к числам определенного вида
В ряде областей науки и техники, например в теории кодирования, важно знать простые числа, близкие к числам определенного вида (чаще всего к степеням таких оснований, как 2, 3 и 10). Вне сомнения, их можно было бы найти в обычных таблицах простых чисел. Однако таблицы нужного размера не могли бы поместиться даже в многотомных изданиях. Поэтому существуют специальные таблицы, в которых приводятся только простые числа, близкие, например, к 2n, 3n и 10n.
Но составить такие таблицы для достаточно больших n довольно трудно, и, несмотря на компактность, такие таблицы зачастую весьма неполны. С помощью системы Mathematica несложно составить такие таблицы самостоятельно. Допустим, таблица должна содержать десять наибольших простых чисел, предшествующих N, и десять простых чисел, следующих за N. Можно ограничиться случаем достаточно больших N, например N>1000, поскольку при меньших N вопрос решается с помощью таблиц простых чисел, помещаемых обычно в учебниках для пятиклассников.
Давайте попытаемся составить нужную нам программу, например, для степеней 10. Чтобы результаты выглядели наглядно, нужно предусмотреть их преобразование в таблицу с помощью текстового процессора, например, Word. Поэтому необходимо предусмотреть такой формат результатов, который было бы легко отформатировать (преобразовать в таблицу). Для этого можно предусмотреть двоеточие : в качества разделителя колонок и два двоеточия : : в качестве разделителя строк таблицы. Вот как может выглядеть программа.
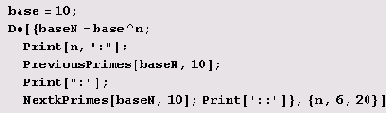
В этой программе использованы функции PreviouskPrimes и NextkPrimes. Функция PreviouskPrimes [N, k] должна генерировать k наибольших простых чисел, меньших Ж Иными словами, она должна генерировать k простых чисел, предшествующих N. Функция NextkPrimes [N, k] должна генерировать k наименьших простых чисел, больших N. Иными словами, она должна генерировать k простых чисел, следующих за N. Вот и все. Нам осталось только написать код этих двух функций. Давайте начнем с функции PreviouskPrimes [N, k].
PreviouskPrimes[n_Integer?(#>100&)
, k_Integer?Positive]:=
Block[{p=PreviousPrime[n] , i=l},
While[i<=k,
{Print[p,","],
p=PreviousPrime[p],++i}]]
Эта функция генерирует простые числа в порядке убывания, т.е. в порядке удаления от заданного числа, что удобно при выборе простого числа, наиболее близкого к заданному.
Не сложнее написать и функцию NextkPrimes [N, k]. Для этого нужно только заменить функцию PreviousPrime на NextPrime.
NextkPrimes[n_Integer?(#>100&) ,
k_Integer?Positive]: = Block[{p=NextPrime[n],i=l},
While[i<=k,{Print[p,","],
p=NextPrime[p] , + + i} ]]
Теперь можем приступить к выполнению составленной программы. Так как функции PreviousPrime и NextPrime содержатся в пакете теории чисел, в первую очередь нужно загрузить этот пакет.
<<NumberTheory`NumberTheoryFunctions`
Затем нужно загрузить (и проверить) определения наших функций PreviouskPrimes и NextkPrimes. Сначала загрузим (и протестируем) PreviouskPrimes.
PreviouskPrimes[n_Integer?(#>100&),
k_Integer?Positive]:= Block[{p=PreviousPrime[n],i=l},
While[i<=k,(Print[p,","],
p=PreviousPrime[p]/++i}]]
PreviouskPrimes[1000,3]
997 ,
991 ,
983 ,
Видим, что функция PreviouskPrimes работает правильно. Значит, теперь можем сделать то же самое и для функции NextkPrimes.
NextkPrimes[n_Integer?(#>100&),
k_Integer?Positive]:= Block[{p=NextPrime[n],i=l},
While[i<=k, {Print[p,","],p=NextPrime[p],++i} ]]
NextkPrimes[1000,3]
1009 ,
1013 ,
1019 ,
Теперь можем ввести программу и выполнить ее. Вот что у нас получится (конец обрезан).
6 : <
999983 999979 999961 999959 999953
999931 999917 999907 999883 999863
1000003 1000033 1000037 1000039
1000081 1000099 1000117 1000121 1000133 1000151
7 :
9999991 ,
9999973 ,
9999971 ,
9999943 ,
Конечно, для практического применения результаты удобнее отформатировать в виде таблицы. Для этого в текстовом редакторе нужно сделать всего несколько замен. Сначала нужно убрать пробелы, разрывы строк, символы абзацев (кроме последнего) и запятые перед двоеточием. Затем два двоеточия нужно заменить символом абзаца. Этим самым мы разобьем таблицу на строки. После этого достаточно выделить все, что получилось, и преобразовать текст в таблицу, указав в качестве разделителя столбцов двоеточие :. Конечно, это еще не все. Нужно ведь еще расставить пробелы после запятых, написать название таблицы и заголовки столбцов.