Наибольший общий делитель — функция GCD

Функция GCD находит наибольший общий делитель в области целых, рациональных и гауссовых чисел.

Наибольший общий делитель в кольце целых чисел

Чтобы найти наибольший общий делитель чисел n₁, n₂, ..., можно использовать функцию GCD [ n₁, n₂, ...]. Вот примеры ее применения для нахождения наибольшего общего делителя двух чисел.

GCD[36,45]

9 GCD[2200 + 3, 3300 + 80]

а=177^5+30621*173^3-173^5 177309584821

b=173^5+30621*177^3-177^5+

151037867129 С=173^4+30621^2+177^4 2814896923

 GCD[a,b] 30637 GCD[а,с] 30637 GCD[b,c]30637

Пример 6.1. Графики функции GCD.

Давайте теперь построим несколько графиков функции GCD. Поскольку это функция двух аргументов, построим изображения поверхности z = GCDflntegerPart [x], IntegerPart [у] ]. Для этого используем функцию Plot3D.

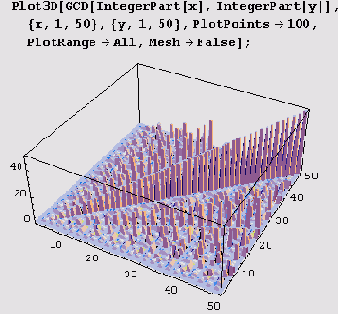
А вот вид вблизи.

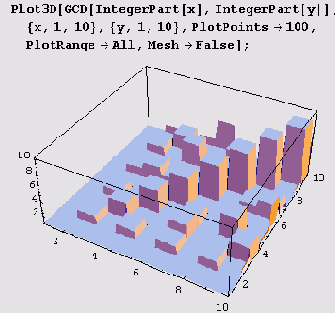
Вот пример нахождения наибольшего общего делителя нескольких чисел.

GCD[Fibonacci[945],Fibonacci[901,Fibonacci[450]]

1134903170

Раз уж мы заговорили о числах Фибоначчи, значит, мы не можем обойти случаи, которые традиционно считаются "наихудшими" для алгоритмов нахождения наибольшего общего делителя.

"Наихудшие" случаи для алгоритмов нахождения наибольшего общего делителя

"Наихудшим" случаем для классического алгоритма Евклида нахождения наибольшего общего делителя считается случай соседних чисел Фибоначчи. Чтобы оценить быстродействие, попытаемся, например, определить, при каком n будет заметна задержка при вычислении GCD[Fibonacci [n+2] (Fibonacci[n+1]]. Возьмем, например, следующую программу.

Do[Print[n,":",GCD[Fibonacci[n+2],Fibonacci[n+1]]],(n, 10000}]

Увы! Алгоритм, реализованный в системе Mathematica, столь эффективен, что даже на весьма посредственном ПК эта программа выполняется без каких бы то ни было задержек. Если же программу модифицировать так: Do[Print[n,":",GCD[Fibonacci[2An+2], Fibonacci[2An+1]]],{n,10000}] ,то задержка будет весьма ощутимой уже при n = 25. Но не забывайте, что 225 + 2 =33554434, а число Fibonacci[2^25+2] имеет 7012462 цифры! Так что алгоритм, реализованный в системе Mathematica, справляется с классическим "наихудшим" случаем не просто вполне удовлетворительно, а блестяще! Правда, известны алгоритмы, для которых наихудший случай представляют числа u = аn +а_n-1, и v= а_n-1, где

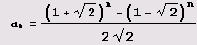
a[n_]:=FullSimplify[((1+Sqrt[2])^n-(1-Sqrt[2])^n)/(2Sqrt[2])]

u:=a[n]+a[n-l]

v:=a[n-l]

Попытаемся выполнить программу.

Do[Print[n,":",GCD{u,v]],{n,100}]

Окажется, что уже при n = 98 выражения "не хотят" упрощаться! Поэтому определение а[n_] лучше изменить.

а[n_]:=(Expand[(1+Sqrt[2])^n]-Expand[(1-Sqrt[2])^n])/(2 Sqrt[2])

Однако при таком подходе понятно, что значительное время тратится также на раскрытие скобок. Однако даже при n = 70 000 вычисления не занимают слишком много времени. При этом значении и числа u и v являются 26 794-значными, и основное время уходит на их вычисление, а не на вычисление их наибольшего общего делителя, который вычисляется в мгновенье ока! Отсюда можем сделать вывод, что функция GCD реализована весьма эффективно, и если при ее использовании возникают неприятности, то, скорее всего, они связаны с вычислением не самой функции, а ее аргументов!

Пример 6.2. Взаимная простота чисел Ферма. Числа Ферма возрастают довольно быстро и являются взаимно простыми. Поэтому их наибольший общий делитель должен быть равен 1. Выясним, до какого номера n система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.

Вот нужная нам функция.

fermat[n_]:=2^(2^n)+1

Теперь можно написать и программу.

Do[Print(n,":",GCD[fermat[n+1], fermat[n]]],{n,100}]

Задержка начинает ощущаться при n = 28. Однако вычисления заканчиваются (и притом довольно быстро, если учитывать количество цифр в числах) и при n= 29. Напомню, что уже 22-е число Ферма имеет более миллиона (1 262 612) знаков, а 23-е число Ферма является 2 525 223-значным! Шутки ради 24-е число Ферма, являющееся 5 050 446-значным, я перетащил в Word. Текстовый редактор с записью этого числа работает медленнее, чем система Mathematica! Вот уж воистину супервычислитель: решает задачу быстрее, чем иные успевают произнести ее формулировку! 25-е число Ферма является 10 100 891-значным, и Word его не выносит: замедляется работа меню, даже курсор движется так медленно, что работать становится практически невозможно.

Пример 6.З. Взаимная простота чисел 2ⁿ -1 и 2^m -1 при взаимно простых лит. Как известно, числа 2ⁿ-1 и 2^m -1 взаимно просты, если взаимно просты пит. Выясним, до какого номера n(предполагая, что т<п) система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.

Вот нужная нам функция.

fn[n_]:=2^n-1

Теперь можно написать и программу.

Dot

Do[

If[GCD[n,m]==1,If[GCD[fn[n], fn[m]]!=l,

Print[n,":",m]]],{m,n-l}],{n,10000}]//Timing

Для первой тысячи чисел все проверки на моем весьма слабеньком ПК выполняются всего лишь за 8,125 секунды! Правда, для проверки этого утверждения в пределах первых десяти тысяч чисел понадобится уже 3398,78 секунды. Здесь, очевидно, сказывается не только увеличение и, но и увеличение временных затрат на нахождение наибольшего общего делителя больших чисел.

Пример 6.4. Наибольший общий делитель чисел, запись которых в десятичной системе состоит из т единиц и n единиц. Как известно, наибольший общий делитель чисел, запись которых в десятичной системе состоит из m единиц и n единиц, является числом того же вида, причем количество единиц в нем равно d= НОД(n, m). Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.

Вот нужные нам определения.

a111[n_]:=(10^n-1) /9 d:= GCD[n, m]

Теперь можно написать и программу.

Dot

Dot

If[GCD[alll[n], a111[m]]!=alll[d],

 Print[n,":",m]],{m,n-l}],{n,1000}]//Timing

Проверка в пределах первой сотни занимает всего лишь 0,234 секунды, хотя при этом наибольшее число указанного в условии вида имеет 100 цифр! Проверка же в пределах первой тысячи у меня потребовала в 200 раз больше — 46,594 секунды. Чтобы выполнить проверку в пределах первых пяти тысяч, потребуется 6879,67 секунды.

Пример 6.5. Наибольший общий делитель чисел аⁿ -1 и а^m -1. Как известно, наибольший общий делитель чисел аⁿ -1 и а^m -1, запись которых в системе счисления с основанием а состоит из n цифр

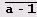
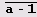является числом того же вида, причем количество цифр й-1 в нем равно d= НОД(n, m). Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.

Вот нужные нам определения.

ааа[а_,n_]:=аЛп-1; d:= GCD[n, m]

Теперь можно написать и программу.

Do[ Dot Dot

If[GCD[aaa[n,a],aaa[m,a]]!=aaa[d],

Print[n,":",m]] ,

{m,n-l}], {n,100}], {a,100}]//Timing

Для выполнения этой программы потребуется 19,797 секунды. Весьма впечатляющий результат!

Пример 6.6. Наибольший общий делитель чисел Фибоначчи. Проверим, что наибольший общий делитель n-го и m-го чисел Фибоначчи равен числу Фибоначчи с номером d = НОД(n, m). Иными словами, проверим, что НОД (Fibonacci [n], Fibonacci [m]) = Fibonacci [НОД (n,m) ]. Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.

Вот нужное нам определение.

d:= GCD[n, m]

Теперь можно написать и программу.

Do[

Do[

If[GCD[Fibonacci[n], Fibonacci[m]]!= Fibonacci[d],

 Print[n,":",m]]

, {m,n-l}],

{n,1000}]//Timing

Для выполнения этой программы потребуется всего лишь 15,75 секунды.

Наибольший общий делитель в поле рациональных чисел

Наибольший общий делитель рациональных чисел r₁, r₂, ... определяется как наибольшее рациональное число г, такое, что все числа r₁/r, r₂ /r, ... являются целыми. Вот пример.

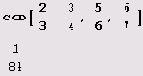
Наибольший общий делитель в кольце гауссовых чисел

Функция GCD может найти наибольший общий делитель не только в кольце целых чисел, но и в кольце целых гауссовых чисел.

GCD[21+28I,-33-44I] 3 + 4 I
Содержание раздела