Алгебра и пакет Mathematica 5
Линейное представление наибольшего общего делителя — функция ExtendedGCD
В ряде задач необходимо найти не только наибольший общий делитель нескольких чисел, но и его представление в виде линейной комбинации этих чисел. Именно эту задачу решает функция
ExtendedGCD. Функция ExtendedGCD [ n1, n2, ...] возвращает список
{g, { r1 , r2, ...}}, такой, что g= GCD [n1,
n2, ...] и g = r1n1+r2n2 + .... Вот примеры.
{g,{r,s}}=ExtendedGCD[n=45,m=36]
(9,{!,-!}}{g,{r,s}}=ExtendedGCD[210°+3,З50 + 8]
{1,{62013782892351778750374,-109502757290992473821761130785} }
Пример 6.7. Единица как линейная комбинация чисел Ферма. Так как числа Ферма являются взаимно простыми, их наибольший общий делитель равен единице. Выясним, как единица представляется в виде линейной комбинации соседних чисел Ферма.
Вот нужная нам функция.
FermatNumber[n_]:=2^(2^n)-N
Теперь можно написать и программу.
Do[Print[n,":",ExtendedGCD[FermatNumber[n+1],
FermatNumber [n]]],{n,10}]
Результаты запишем в виде таблицы.
Заметьте, что в таблице при n>1 числа rn заканчиваются цифрой 8, а числа sn— цифрой 1.
Пример 6.8. Единица как линейная комбинация чисел 2n-1 и 2m-— 1 при взаимно простых пит. Так как числа 2n -1 и 2m -1 взаимно просты, если взаимно просты n и m, то единицу можно представить в виде линейной комбинации чисел 2n -1 и 2m-1 при взаимно простых пит. Выясним, до какого номера n(предполагая, что т<п) система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.
Вот нужная нам функция.
fn[n_]:=2^n-1
Теперь можно написать и программу.
Do[
Dot
If[GCD[n, m]==l, Print[n,":",m, ":",
ExtendedGCD[fn[n],fn[m]]]],{m,n-l}],(n,10}]
Результаты запишем в виде таблицы .
Заметьте, что довольно часто в данной таблице встречается пара r = 1,5= -2. Это не случайно, поскольку при n = n+1 выполняется равенство -(2n -1)+2-(2(n -1) = -1.
Пример 6.9. Линейное представление наибольшего общего делителя чисел, десятичная запись которых состоит из m единиц и n единиц. Наибольший общий делитель чисел, десятичная запись которых состоит из т единиц и п единиц, является числом того же вида, причем количество единиц в нем равно d = НОД(n, m). Выясним, как он представляется в виде линейной комбинации.
Вот нужные нам определения.
a111[n]:=(10^n-1)/9 d: = GCD[n, m]
Теперь можно написать и программу:
Dot
Dot
Print[n,":",m,":",
ExtendedGCD[alll[n],alll[m]]],{m,n-l}],{n,10}]
Заметьте, что десятичная запись чисел r и s в данной таблице содержит только цифры 0 и 1. Я не удивлюсь, если вы предположите, что это связано с наличием некоторых полиномиальных тождеств и потому значения г и s получаются в результате подстановки 10 (основания системы счисления) в них. Например, строку таблицы
| 9 |
6 |
111 |
1 |
-1000 |
можно истолковать так:
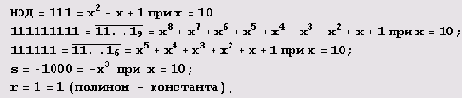
s = -1000 = -x3 при х = 10;
r = 1 = 1(полином-константа); поэтому
х2 +х + 1 = 1*(x8 +х7 + х6 + х5
+ х4 + х3+х2 +х + 1) + (-x3)-(x5 +х4 +
x3 + х2 +х+ 1) при х = 10. Однако само это равенство выполняется при любом
g:, а не только при дс = 10. Значит, в качестве г и s можно взять числа, имеющие точно такое же представление в любой системе счисления, а не только в десятичной! Конечно, наличие строки в таблице еще не означает автоматически тождественную справедливость соответствующего равенства, это лишь означает, что соответствующее равенство справедливо при х = 10. Поэтому вполне возможно, по крайней мере теоретически, что нам просто повезло. Если говорить честно, так оно и есть. Дело ведь в том, что по равенству d = ra+sb (d = НОД(a,
b)) числа r и s определяются неоднозначно: если d = ra+sb, то d = (r+b)a+(s—a)b и d = (r—b)a+(s+a)b. Иными словами, если d = ra+sb, то d= r'a+s'b (при r'= r+b и s' = s-а) и d— r"a+s"b (при r" = r-b и s"= s+d). Так что наличие строки еще не означает наличие тождества. Но, с другой стороны, числа г и s определяются однозначно, если на них наложить ограничения
|r <b и |s| <a. Более того, все пары значений г и s можно получить, несколько раз выполняя переход от какой-либо пары фиксированных значений г0 и s0 к новой паре значений по правилам г' =
г+b и s'= s-a или r' = r-b и s'= s+a.
Конечно, наличие полиномиальных тождеств сомнений не вызывает, ведь наибольший общий делитель полиномов (х) =
xn-1 + хn-2 + xn-3 +... + х +1 и b(х) = хm-1+хm-2+хm-3 + ... + х+1 равен d(x) = xd-1 + xd-2 +
хd-3 +... + х +1, где d = НОД(n ,m).
Так как он представим в виде линейной комбинации а(х) — хn-1 + хn-2 + хn-3 +... + х +1 и
b(х) = хm-1 + хm-2 + хm-3 +... + х+1, то имеет место равенство d(x) = r(x)a(x)+s(x)b(x). Более того, полиномы г(х) и s(x) можно выбрать так, чтобы deg r(x)<m и deg s(x)<n. Проблема, собственно, состоит вот в чем. По числам а и b мы без труда восстановили полиномы а(х) =
xn-1+ хn-2 + xn-3 +... + xn +1 и b(х)
=хn-1+хn-2+хn-3+... + х + 1, но можем ли мы так же просто восстановить и полиномы г(х) и 5(х)?
Предположим теперь, что для равенства d = ra+sb (d = НОД(я, b)) с \r\ <b и \s\ <a мы написали равенство полиномов того же типа, что и приведенное выше. Запишем это равенство в виде d(x) = r(x)a(x)+s(x)b(x). Разумеется, здесь а(х) = хn-1+хn-2+хn-3+... + х + 1 и
b(х) = xn-1 +хn-2+ хn-3+ ... + Х + ] .Поскольку
a<b и |s| <a, то deg r(x)<m и deg s(x)<n, а потому правая часть найденного тождества есть полином степени не выше
m+n. Тогда, как известно, чтобы проверить написанное равенство, достаточно проверить его при т+п+1 значении х. (Конечно, такую проверку совсем несложно запрограммировать в системе Mathematica.) Но можно поступить и иначе. Достаточно убедиться, что представление г и s будет одинаковым для т+п+1 значений основания системы счисления. (Ведь фактически это будет означать, что равенство полиномов степени не выше
m+n выполняется при n+m+1 значении х.) Именно таким способом мы и поступим в следующем примере. (Вопрос о том, есть ли среди найденных представлений такие, которые основаны не на полиномиальных тождествах, намеренно оставляю открытым. Впрочем, вот подсказка: ответ знают некоторые студенты мехмата уже на первом семестре. Я, конечно, совсем не имел в виду, что это написано в учебниках или обязательно излагается на лекциях, но догадаться можно.)
Пример 6.10. Линейное представление наибольшего общего делителя чисел аn-1 и
аm -1. Наибольший общий делитель чисел а" -1 и а" -1, запись которых в системе счисления с основанием а состоит из и цифр
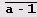
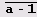 , является числом того же вида, причем количество цифр я-1 в нем равно d= НОД(n,
m). Выясним, как наибольший общий делитель чисел аn -1 и аm -1 представляется в виде их линейной комбинации.
, является числом того же вида, причем количество цифр я-1 в нем равно d= НОД(n,
m). Выясним, как наибольший общий делитель чисел аn -1 и аm -1 представляется в виде их линейной комбинации.
Вот нужные нам определения.
ааа[а_,n_]:=аАп-1; d:= GCD[n, m]
Теперь можно написать и программу. Нужно только не забыть о том, что представление
r и s лучше всего получить в системе счисления с основанием я. Для этого вполне подойдет функция
IntegerDigits. Она, правда, теряет знак числа, так что его придется печатать отдельно.
Do[ Dot Dot
{{g,(r,s}}= ExtendedGCD[aaa[a,n],aaa[a,m]],
Print["###", n, ":",m,":",d,":",a,":"],
If[g<0,Print["-"]],
Print[IntegerDigits[g,a], ":"],
If[r<0,Print!"-"]],
Print[IntegerDigits[r,a], ":"],
If [s<0,Print["-"]],
Print[IntegerDigits[s,a]]} ,
{a,2,n+m+2}],{m,n-l}],{n,10}]
Заметьте, что в программе вставлена печать fit для удобства форматирования результатов.
Скажу сразу, что более скучной таблицы я, наверное, никогда не видел! И все из-за удивительного постоянства г и s! Представление r и s выглядит одинаково в системах счисления с разными основаниями, и потому их представления просто повторяются во многих строках! Это значит, что представление наибольшего общего делителя действительно основано на полиномиальных тождествах вида d(x) = r(x)a(x)+s(x)b(x), причем полиномы r(х) и s(x) легко восстанавливаются по числам r и s! Конечно, я избавлю вас от демонстрации всего этого и просто приведу некоторые наиболее характерные строки таблицы. Разумеется, большинство строк an опустил, и таблица содержит пропуски. Они обозначены строками с многоточиями. Чтобы развеять сомнения, достаточно взглянуть вот на это.
Линейное представление наибольшего общего делителя чисел аn - 1 и аm -1:
НОД= r-(an-l) + s-(am-l)
| n |
m |
d= НОД (n, m) |
Основание системы счисления а |
Цифры НОД в системе счисления с основанием а |
Цифры r в системе счисления с основанием а |
Цифры s в системе счисления с основанием а |
| 2 |
1 |
1 |
2 |
(1) |
{0} |
{1} |
| 2 |
1 |
1 |
3 |
{2} |
{0} |
(1) |
| 2 |
1 |
1 |
4 |
{3} |
{0} |
{1} |
| 2 |
1 |
1 |
5 |
Н) |
{0} |
(1) |
| 3 |
1 |
1 |
2 |
{1} |
{0} |
{1} |
| 3 |
1 |
1 |
3 |
{2} |
{0} |
{1} |
| 3 |
1 |
1 |
4 |
{3} |
{0} |
{1} |
| 3 |
1 |
1 |
5 |
{4} |
{0} |
(1) |
| 3 |
1 |
1 |
6 |
(5) |
{0} |
{1} |
| 3 |
2 |
1 |
2 |
(1) |
{1} |
-{1,0} |
| 3 |
г |
1 |
3 |
(2} |
{1} |
-{1,0} |
| 3 |
2 |
1 |
4 |
(3) |
{1} |
-{1,0} |
| 3 |
2 |
1 |
5 |
(4} |
{1} |
-{1,0} |
| 3. |
2 |
1 |
6 |
(5) |
{1} |
-{1,0} |
| 3 |
2 |
1 |
7 |
(6) |
{1} |
-{1,0} |
| 4 |
1 |
1 |
2 |
(1} |
{0} |
{1} |
| 4 |
1 |
1 |
3 |
{2} |
{0} |
{1} |
| 4 |
1 |
1 |
4 |
(3) |
{0} |
{1} |
| 4 |
1 |
1 |
5 |
(4) |
{0} |
{1} |
| 4 |
1 |
1 |
6 |
{5} |
(0) |
{1} |
| 4 |
1 |
1 |
7 |
{6} |
{0} |
{1} |
| 4 |
2 |
2 |
2 |
{1,1} |
{0} |
{1} |
| 4 |
2 |
2 |
3 |
(2,2) |
{0} |
{1} |
| 4 |
2 |
2 |
4 |
(3,3) |
{0} |
{1} |
| 4 |
2 |
2 |
5 ' |
{4,4} |
{0} |
{1} |
| 4 |
2 |
2 |
6 |
{5,5} |
{0} |
{1} |
| 4 |
2 |
2 |
7 |
{6,6} |
{0} |
{1} |
| 4 |
2 |
2 |
8 |
(7,7} |
{0} |
{1} |
| 4 |
3 |
1 |
2 |
{1} |
{1} |
-{1,0.} |
| 4 |
3 |
1 |
3 |
{2} |
{1} |
-{1,0} |
| 4 |
3 |
1 |
4 |
{3} |
{1} |
-{1,0} |
| 4 |
3 |
1 |
5 |
{4} |
{1} |
-{1,0} |
| 4 |
3 |
1 |
6 |
{5} |
{1} |
-{1,0} |
| 4 |
3 |
1 |
7 |
{6} |
{1} |
-{1,0} |
| 4 |
3 |
1 |
8 |
{7} |
{1} |
-{1,0} |
| 4 |
3 |
1 |
9 |
(81 |
(1) |
-{1,0} |
| .. | ... | ... | ... | ... | ||
| 5 |
2 |
1 |
2 |
{1} |
{1} |
-{1,0,1,0} |
| 5 |
2 |
1 |
3 |
(2) |
{1} |
-{1,0,1,0} |
| 5 |
2 |
1 |
4 |
(3} |
{1} |
-{1,0,1,0} |
| 5 |
2 |
1 |
5 |
(4) |
{1} |
-{1,0,1,0} |
| 5 |
2 |
1 |
6 |
{5} |
{1} |
-{1,0,1,0} |
| 5 |
2 |
1 |
7 |
{6} |
{1} |
-{1,0,1,0} |
| 5 |
2 |
1 |
8 |
{7} |
{1} |
-{1,0,1,0} |
| 5 |
2 |
1 |
9 |
(8) |
{1} |
-{1,0,1,0} |
| 5 |
3 |
1 |
2 |
(1) |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
3 |
{2} |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
4 |
(3} |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
5 |
{4} |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
6 |
{5} |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
7 |
{6} |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
8 |
{7} |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
9 |
(8) |
-{1,0} |
{1,0,0,1} |
| 5 |
3 |
1 |
10 |
{9} |
-{1,0} |
{1,0,0,1} |
| 5 |
4 |
1 |
2 |
{1} |
{1} |
-{1,0} |
| 5 |
4 |
1 |
3 |
{2} |
{1} |
-{1,0} |
| 5 |
4 |
1 |
4 |
(3) |
{1} |
-{1,0} |
| 5 |
4 |
1 |
5 |
{4} |
{1} |
-{1,0} |
| 5 |
4 |
1 |
6 |
(5} |
{1} |
-{1,0} |
| 5 |
4 |
1 |
7 |
{6) |
{1} |
-{1,0} |
| 5 |
4 |
1 |
8 |
{1} |
{1} |
-{1,0} |
| 5 |
4 |
1 |
9 |
{8} |
{1} |
-{1,0} |
| 5 |
4 |
1 |
10 |
{9} |
{1} |
-{1,0} |
| 5 |
4 |
1 |
11 |
{10} |
{1} |
-{1,0} |
| ... |
... | ... | ... |
... | ... | |
| 7 |
2 |
1 |
2 |
{1} |
11} |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
3 |
(2) |
{1} |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
4 |
{3} |
{1} |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
5 |
{4} |
{1} |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
6 |
{5} |
{1} |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
7 |
{6} |
{1} |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
8 |
(7) |
(1) |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
9 |
{8) |
{1} |
-{1,0,1,0, 1,0} |
| 7 |
2 |
1 |
10 |
{9} |
{1} |
-{1,0,1,0,1,0} |
| 7 |
2 |
1 |
11 |
{10} |
{1} |
-{1,0,1,0,1,0} |
| 7 |
3 |
1 |
2 |
{1} |
{1} |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
3 |
{2} |
(1) |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
4 |
{3} |
{1} |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
5 |
{4} |
{1} |
-{1,0,0,1,0} |
| 7 |
3 |
1 i |
6 |
{5} |
{1} |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
7 |
{5} |
{1} |
-{1,0,0, 1,0} |
| 7 |
3 |
1 |
8 |
{8} |
{1} |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
9 |
{8} |
{1} |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
10 |
{9} |
(1) |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
11 |
{10} |
{1} |
-{1,0,0,1,0} |
| 7 |
3 |
1 |
12 |
{11} |
{1} |
-{1,0,0,1,0} |
| 7 |
4 |
1 |
2 |
{1} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
3 |
{2} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
4 |
{3} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
5 |
{4} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
6 |
{5} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
7 |
{6} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
8 |
{7} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
9 |
{8} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
10 |
{9} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
11 |
{10} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
12 |
{11} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
4 |
1 |
13 |
{12} |
-{1,0} |
{1,0,0,0,1} |
| 7 |
5 |
1 |
2 |
{1} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
3 |
{2} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
4 |
{3} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
5 |
{4} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
6 |
{5} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
7 |
{6} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
8 |
{1} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
9 |
{8} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
10 |
{9} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
11 |
{10} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
12 |
(11) |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
13 |
{12} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| 7 |
5 |
1 |
14 |
{13} |
-{1,0,1,0} |
{1,0,1,0,0,1} |
| ... | ... | ... | ... |
... | ||
| 8 |
3 |
1 |
2 |
{1} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
3 |
{2} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
4 |
{3} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
5 |
{4} |
-{1,0-} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
6 |
{5} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
7 |
{6} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
8 |
{7} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
9 |
{8} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
10 |
{9} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
11 |
{10} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
12 |
{11} |
-{1,0} |
{1,0,0,1,0,0,1} |
| 8 |
3 |
1 |
13 |
{12} |
-{1,0} |
{1,0,0,1,0,0,1} |
| ... |
... | ... | ... | ... | ... | |
| 8 |
5 |
1 |
2 |
{1} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
3 |
(2). |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
4 |
{3} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
5 |
{4} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
6 |
(5} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
7 |
{6} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
8 |
{7} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
9 |
{8} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
10 |
{9} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
11 |
{10} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
12 |
(И) |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
13 |
{12} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
14 |
{13} |
{1,0,0,1} |
-{1,0,0,1,0,1,0} |
| 8 |
5 |
1 |
15 |
{14} |
{1,0,0,1} |
-(1,0,0,1,0,1,0) |
| ... |
... | ... | ... | ... |
... | |
| 10 |
6 |
2 |
2 |
(1,1) |
-{1,0,0} |
{1,0,0,0,0,0,1} |
| 10 |
6 |
2 |
3 |
{2,2} |
-{1,0,0} |
{1,0,0,0,0,0,1} |
| 10 |
6 |
2 |
4 |
{3,3} |
-{1,0,0} |
{1,0,0,0,0,0,1} |
| 10 |
6 |
2 |
5 |
{4,4} |
-{1,0,0} |
{1,0,0,0,0,0,1} |
| 10 |
6 |
2 |
6 |
{5,5} |
-{1,0,0} |
{1,0,0,0,0,0,1} |
| 10 |
6 |
2 |
7 |
{6,6} |
-{1,0,0} |
{1,0,0,0,0,0,1} |
| id |
6 |
2 |
8 |
(7,7) |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
9 |
(8,8} |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
10 |
(9,9) |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
11 |
(10,10} |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
12 |
(11,11} |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
13 |
(12,12} |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
14 |
(13,13} |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
15 |
(14,14} |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
16 |
(15,15} |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
17 |
(16,16) |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
6 |
2 |
18 |
(17,17) |
-(1,0,0) |
(1,0,0,0,0,0,1) |
| 10 |
7 |
1 |
2 |
(1) |
-(1,0,0,1,0) |
(1,0,0,1,0,0,0,1) |
| 10 |
1 |
1 |
3 |
(2} |
-(1,0,0,1,0) |
(1,0,0,1,0,0,0,1) |
| 10 |
1 |
1 |
4 |
(3} |
-(1,0,0,1,0) |
(1,0,0,1,0,0,0,1) |
| 10 |
1 |
1 |
5 |
(4} |
-(1,0,0,1,0) |
(1,0,0,1,0,0,0,1) |
| 10 |
1 |
1 |
6 |
(5} |
-(1,0,0,1,0) |
{1,00, 1,0, 0,0,1} |
| 10 |
1 |
1 |
7 |
(6} |
-(1,0,0,1,0) |
{1,0,10,1,0,0,0,1} |
| 10 |
1 |
1 |
8 |
(7) |
-(1,0,0,1,0) |
{1,0,:0, 1,0, 0,0,1} |
| 10 |
7 |
1 |
9 |
(8} |
-(1,0,0,1,0) |
{1,0,0,1,0,0,0,1} |
| 10 |
7 |
1 |
10 |
(9) |
-{1,0,0,1,0} |
(1,0,0,1,0,0,0,1) |
| 10 |
7 |
1 |
11 |
(10} |
-(1,0,0,1,0} |
(1,0,0,1,0,0,0,1) |
| 10 |
7 |
1 |
12 |
(11) |
-(1,0,0,1,0) |
(1,0,0,1,0,0,0,1) |
| 10 |
7 |
1 |
13 |
(12) |
-(1,0,0,1,0} |
(1,0,0,1,0,0,0,1) |
| 10 |
7 |
1 |
14 |
(13) |
-(1,0,0,1,0} |
(1,0,0,1,0,0,0,1) |
| 10 |
7 |
1 |
15 |
(14) |
-(1, 0,0,1,0} |
(1,0,0,1,0,0,0,1) |
| 10 |
7 |
1 |
16 |
(15) |
-{1, 0,0,1,0} |
(1,0,0,1,0,0,-0,1) |
| 10 |
7 |
1 |
17 |
(16) |
-(1,0,0,1,0) |
{1,0,0,1,0,0,0,1} |
| 10 |
7 |
1 |
18 |
(17} |
-(1,0,0,1,0) |
(1,0,0,1,0,0,0,1} |
| 10 |
7 |
1 |
19 |
(18} |
-(1,0,0,1,0) |
(1,0,0,1,0,0,0,1} |
| ... |
... | ... | ... | ... |
Честно говоря, возникает желание избавиться от этого назойливого повторения. Как это сделать? Для этого придется переделать программу. Но чтобы программа не была слишком длинной, лучше переписать ее. Прежде всего, к уже имеющимся определениям
ааа[а_,n_]:=аАп-1; d:= GCD[n, m]
добавим еше два для печати.
prnt : = {Print["###",n, ":",m,":",d,":",a,":"],
If[g<0,Print["-"]],
Print[IntegerDigits[g,a],":"],
If[r<0,Print["-"]],
Print[IntegerDigits[r,a],":"],
If [s<0-. Print ["-"] ] ,
Print[ IntegerDigits [s, a] ] };
prnt1:={Print["%%%",n,":",m,":",d,":"],
If[r<0, Print["-"]],
Print[FromDigits!IntegerDigits[r,a],10],":"],
If[s<0,Print!"-"]];
Print[FromDigits[IntegerDigits[s,a],10]]);
Основным определением здесь является prntl. Именно это определение используется для первого вывода на печать значений n, m, d = НОД(n, m), а также двоичных представлений rus. Чтобы облегчить распознавание определения, которое выполняет печать, в основном определении (prntl) ведущими символами являются ###, а во вспомогательном (prnt) — %%%. Используя вспомогательное определение prnt, предыдущую программу можно переписать так.
Do[
Do[
Do[{{g,{r,s)}=ExtendedGCD[aaa[a,n],aaa[a,m]], prnt},
{a,2,n+m+2}], {m,n-l}], {n,10}] Вспомогательное определение prnt будет использоваться для первого вывода на печать только тех представлений г и s, которые отличаются от первого. Поэтому в этом определении предусмотрен вывод дополнительной информации: представления g и основания системы счисления а.
Теперь программу можно модифицировать с учетом нового определения функции печати. Возникает соблазн написать программу так.
Do[
Do[{
Do[{{g,{r,s}}=ExtendedGCD[aaa[a,n],aaa[a,m]],
If[a==2,{{g0,{r0,s0}}={g,(r,s)}, prntl}],
If[{g0,{r0,s0}}!={g,{r,s}},prnt]},{a,2,n+m+2}]},{m,n-l}],{n,10}] Но это совсем не то, что мы хотели! Ведь условие {g0, {r0, s0}} ! = {g, {r, s}} будет выполнено при а! =2. Все дело в том, что значения ms зависят от основания системы счисления а\ Не зависит от основания системы счисления а лишь их представление в системе счисления с основанием а. Поэтому проверять нужно именно неизменность представления в системе счисления с основанием а. Кроме того, проверка g0! =n лишняя. Поэтому лучше добавить еще одно определение.
newrs:=
{ Signfr0], Signts0], IntegerDigits[r0,2],
IntegerDigits[s0,2] } != { Sign[r], Sign[s],
IntegerDigits[r, a], IntegerDigits[s, a] }
Теперь можно записать программу.
Do[
Do [{
Do[{{g,{r,s}}=ExtendedGCD[aaa[a,n],aaa[a,m]],
If[a==2,{ {r0,s0}={r,s}, prntl}], If[newrs,prnt]},
{a,2,n+m+2H }, {m,n-l} ]; {n,20}]
Теперь выполним программу. Сколько раз сработала вспомогательная печать? Ни разу! Это значит, что по всем найденным значениям г и s можно восстановить многочлены г(х) и s(x) и написать тождество d(x) = r(x)a(x)+s(x)b(x)\ Полученные результаты стоят того, чтобы собрать их в таблицу (табл. Б.33).
Полученная таблица заслуживает более внимательного рассмотрения. Рассмотрим, например, одну строку таблицы.
| 20 |
17 |
1 |
1001001001001001 |
-1001001001001001010 | |
Так как d(x) = xd -I = лс-1, эта строка означает, что х-1 = d(x) = r(x)a(x)+s(x)b(x), где а(х)= JC20-1, 'b(х) = хn-1,
r(х) = 1+x3+x6+х9+x12+x15,
s(x) =-(х+х3+ х6+x9+х12+ х15+х18). Иными словами, она означает, что х-1 = d(x) =r(х) (х20 -1) +s(x) (хn -1) для указанных только что полиномов г(х) и s(x).
Впрочем, вместо r(x) и s(x) можно подставить их выражения, и тогда получится следующее тождество:
x-1 = (1+х3+x6+x9+x12+x15) (х20-1) -(х+х3 + х6+х9
+ х12+х15 +х18) (х17-1).
Таким образом, мы видим, что каждая строка полученной таблицы фактически основана на полиномиальном тождестве и фактически является кратким его кодом!
Давайте теперь сравним полученные значения для г и s в равенстве НОД(a, b) = ra+sb для а = хn-1
-1, b= хm+1 -1 (х целое) с теми, которые были получены ранее для такого же равенства для чисел а и
b, десятичная запись которых состоит из т единиц и n единиц. (Нужную таблицу мы подготовили заранее.) Не случайно ли значения г и s совпадают? Нет, не случайно. Дело в том, что если справедливо равенство НОД(а,-
b) = ra+sb для а = хn-1 -1, b = xm+1 -1 (х целое, отличное от 1), то
справедливо и равенство
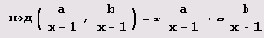
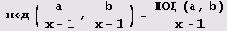 .
(Напомню, что числа
.
(Напомню, что числа
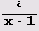
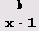 целые при целом х
и а = хn+1 -1, b = xm+1 -1.) Более того, запись чисел
целые при целом х
и а = хn+1 -1, b = xm+1 -1.) Более того, запись чисел
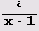
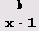 в системе счисления
с целым основанием х как раз и состоит из n единиц и m единиц. Поскольку равенства НОД(а, b) = ra+sb и
в системе счисления
с целым основанием х как раз и состоит из n единиц и m единиц. Поскольку равенства НОД(а, b) = ra+sb и
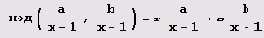 n+1-1, b= хm+1-1
(х целое, отличное от 1) равносильны, то г и s принимают в них одинаковые значения. Отсюда, в частности, следует, что если числа
r и s из равенства НОД(а,b) = ra+sb имели одно и то же представление для любого основания системы счисления х, то же самое будет справедливо и для чисел
r и s из равенства
n+1-1, b= хm+1-1
(х целое, отличное от 1) равносильны, то г и s принимают в них одинаковые значения. Отсюда, в частности, следует, что если числа
r и s из равенства НОД(а,b) = ra+sb имели одно и то же представление для любого основания системы счисления х, то же самое будет справедливо и для чисел
r и s из равенства
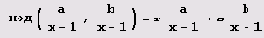 n+1-1, b= хm+1-1,
n+1-1, b= хm+1-1,
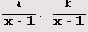 n+1 -1 и
b = xm+1 -1, фактически отличаются только множителем х-1. Например, из тождества
x-1 = (1+х3+x6+x9+x12+x15) (х20-1) -(х+х3 + х6+х9
+ х12+х15 +х18) (х17-1). получается еще более длинное тождество:
n+1 -1 и
b = xm+1 -1, фактически отличаются только множителем х-1. Например, из тождества
x-1 = (1+х3+x6+x9+x12+x15) (х20-1) -(х+х3 + х6+х9
+ х12+х15 +х18) (х17-1). получается еще более длинное тождество:
1 =x-1 = (1+х3+x6+x9+x12+x15) (х20-1) -(х19
+ х18+х17 +...+х+1) -(1+х3+x6+x9+x12+x15+x18)
*(х16 + х15+х14 +...+х+1)
Обратите, наконец, внимание на то, что в полученной таблице представления чисел
r и s содержат только нули и единицы. Это означает, что коэффициенты полиномов r(х) и s(x), построенных по представлениям чисел
r и s, тоже будут равны 0 и 1 (либо - 1, если перед представлением стоит знак минус).