Алгебра и пакет Mathematica 5
Наименьшее общее кратное — функция LCM
Во множестве всех кратных нескольких данных чисел всегда найдется такое, которое является делителем всякого другого общего кратного этих чисел: это — общее наименьшее кратное.
Функция LCM находит наименьшее общее кратное в области целых, рациональных и гауссовых чисел.
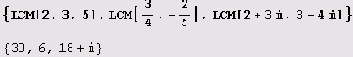
Что такое наименьшее общее кратное нескольких рациональных чисел? Это, конечно, такое наименьшее рациональное число, частные от деления которого на данные рациональные числа являются целыми.
Пример 6.11. Наименьшее общее кратное первой тысячи чисел. Вот как можно его найти.

Это, конечно же, существенно меньше, чем 1000!. В

раз! Заметьте, что наименьшее общее кратное первой тысячи чисел заканчивается всего лишь четырьмя нулями.
Пример 6.12. Графики функции LCM.
Давайте теперь построим несколько графиков функции LCM. Поскольку это функция двух аргументов, построим изображения поверхности
z = LCM[IntegerPart [x], IntegerPart [у] ]. Для этого используем функцию Plot3D.
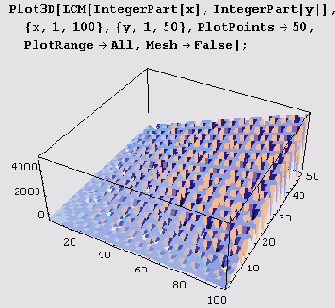
А вот вид вблизи.