Остаток от деления — функция Mod

Чтобы получить остаток от деления n на m, нужно воспользоваться функцией Mod[n,m]. Наименьший возможный остаток в этом случае равен нулю, а наибольший... Как вы думаете, чему равен наибольший возможный остаток? "Конечно, m-1", — возможно, подумали вы. Ну, что же, я, конечно, приветствую ваши глубокие познания в теории чисел, ибо именно так написано во всех классических учебниках по этой дисциплине, если, конечно, именно в этом месте нет какой-либо досадной опечатки. Но должен вас разочаровать: вы не угадали. Зато, надеюсь, вам будет приятно узнать, что возможности функции Mod значительно шире, чем требуется для решения задач из задачников по классической теории чисел. Дело в том, что аргументы этой функции могут быть не только целыми (это предусмотрено классическими учебниками теории чисел), но и вещественными и даже комплексными! А во множестве вещественных чисел, как вы, надеюсь, еще помните, полно сюрпризов... Но сначала давайте рассмотрим простейший случай целых аргументов.

Mod[7,5]

2

Ну вот, при делении 7 на 5 остаток равен 2. Просто и понятно, даже в уме можно вычислить. Вот еще один пример.

Мод[3^10,5]

4

Тоже в уме, и тоже просто и понятно. Но вот несколько примеров с вещественными числами.

Теперь, надеюсь, вы поняли, что множество значений Mod[n,m] не имеет набольшего элемента. Можно лишь утверждать, что при вещественных m и n 0<Mod [n, m] <m, причем все значения из открытого справа интервала [0, m) функция Mod[n,m] принимает. Но иногда нужно сдвинуть этот интервал на d. Нет проблем: укажите сдвиг d третьим параметром.

Вот как можно найти остатки от деления чисел 0, 1,2, ..., 21 на 3.

Mod[Range[0,21],3]

{0,1,2,0,1,2,0,1,2,0,1,2,0,1,2,0,1,2,0,1,2,0}

А вот те же остатки, когда задан сдвиг 1.

Mod[Range[0, 21] ,3,1]

{3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3}

А вот те же остатки, когда задан сдвиг 2.

Mod[Range[0,21],3,2]

{3,4,2,3,4,2,3,4,2,3,4,2,3,4,2,3,4,2,3,4,2,3}

Ниже приведены основные свойства функций Quotient и Mod:

n*Quotient[m, n, d] + Mod[m, n, d] = m при любых допустимых m, n, d;
знак Mod [m, n] совпадает со знаком и при любых допустимых вещественных m, n;
Mod[m, n] = m-n*Quotient [m, n] при любых допустимых m, n;
Mod [m, n, d] = m-n*Quotient [т, n, d] при любых допустимых m, n, d;
Mod[x, 1] равно дробной части х

Ну и, наконец, полезно иметь в виду, что аргументы функции Mod могут быть списками. Это, например, позволяет найти остаток от деления данного числа сразу на несколько чисел.

Mod[244, {4, 9, 121}]

{0,1,2} ,

Можно также найти остатки от деления нескольких чисел на заданное число.

Mod[{0,l,2,3,4)A2,5]

{0,1,4,4,1}

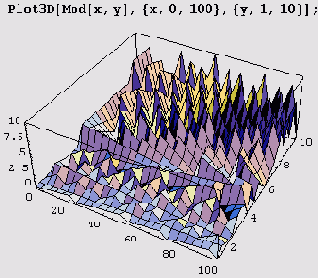
Пример 7.2. Графики функции Mod.

Теперь давайте построим несколько графиков функции Mod. Поскольку это функция двух аргументов, построим изображения поверхности z = Mod[x, у]. Для этого используем функцию Plot3D.

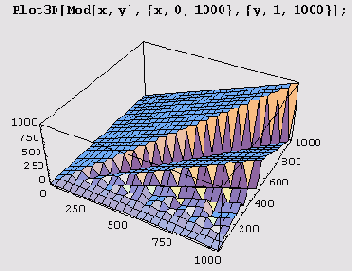
А вот вид вблизи.

Содержание раздела