Алгебра и пакет Mathematica 5
Квадратный корень по модулю — функции SqrtMod и SqrtModList
Конечно, квадратных корней в системе остаточных классов — решений сравнения х =d (mod n) — может быть более одного. Поэтому в системе Mathematica предусмотрено две функции для нахождения таких решений. Функция SqrtMod находит наименьший вычет, а функция SqrtModList — Список всех вычетов.
Наименьший квадратный корень по модулю — функция SqrtMod
Выражение SqrtMod[d, n] представляет собой наименьший неотрицательный квадратный корень из d по модулю n, т.е. такой наименьший неотрицательный вычет m,
что m2sd(modn). Но это, конечно, в том случае, если такое т существует. Для этого d, понятно, должно быть полным квадратом по модулю и, т.е. символ Якоби .jacobiSymbol [d, n] должен быть равным 1. Это условие также достаточно, если и является простым числом. Для простых n система Mathematica использует алгоритм Шенкса (Shanks). Для примера найдем самое маленькое неотрицательное целое число, такое, что его квадрат равен 3 по модулю 11.
SqrtMod[3,11] 5
Этот результат легко проверить.
Mod[Range[11]^2,11]
{1,4,9,5,3,3,5,9,4,1,0}
Как видите, только квадраты чисел 5 и 6 по модулю 11 равны 3. Если квадратный корень из d по модулю п не существует, SqrtMod [d, n] останется невычисленным.
Убедимся, например, что квадратный корень из 3 по модулю 5 не существует.
Mod[{0,l,2,3,4}*2,5]
{0,1,4,4,1}
Ну и, конечно, нельзя не пройти мимо вычисления квадратного корня из 2.
SqrtMod[2,1СГ64+57]//Timing
{0.016
Second,876504467496681643735926111996546100401033611976777074909122865 }
Функция SqrtMod может вычислять квадратные корни не только по простому модулю, но и по составному.
Однако не всегда такие вычисления происходят мгновенно. Для вычисления квадратного корня приходится разлагать модуль на множители, и потому для очень больших составных модулей функция SqrtMod далеко не всегда дает результат.
Список всех квадратных корней по модулю — функция SqrtModList
Как мы только что видели, квадратных корней может не быть совсем, а может быть несколько. Список всех квадратных корней из данного числа по заданному модулю дает функция SqrtModList. Если квадратных корней нет, список, естественно, будет пустым. Вот пример, когда существует два квадратных корня.
SqrtModList[3,11]
{5,6}
А вот пример, когда квадратных корней нет совсем.
SqrtModList[2,11]
{}
Существование квадратного корня по модулю и символ Якоби — функция JacobiSymbol
Как узнать, существует ли квадратный корень из данного числа d по модулю и? Иногда для этого достаточно вычислить символ Якоби
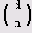
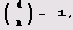го d является квадратичным невычетом по модулю d. Если же Якоби
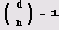
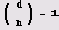то о квадратичности
вычета d по модулю и судить непосредственно нельзя.) Для вычисления символа Якоби в системе Mathematica предусмотрена функция JacobiSymbol [d, n]. Число 2 не является квадратичным вычетом по модулю 13, а число 4 является таковым (по любому модулю).
{JacobiSymbol[2,13],JacobiSymbol[4,13]}
{-1,1}
