Алгебра и пакет Mathematica 5
Простые числа Мерсенна, тест Люка-Лемера
Наибольшее простое число поймано решетом Эратосфена.
Конечно, решето Эратосфена годится для поиска простых чисел Мерсенна не более чем консервная банка для плавания через Атлантический океан. Гораздо более пригодна для этой цели функция PrimeQ. С ее помощью мы нашли все те индексы простых чисел Мерсенна, которые не превышают 5000. Дальнейшее продвижение оказалось практически невозможным. Однако есть другой метод проверки простоты чисел этого вида. Его опубликовал Э. Люка (Lukas2) в 1878 году, а в 1930 году усовершенствовал Д. X. Лемер. Он основан на следующей теореме.
Если р>2 — простое число, то число Мерсенна Мр = 2p -1 является простым тогда и только тогда, когда bр_r = О, где последовательность L; определяется так:
L0 =4, Li+1=(Li2-2)mod(2i-l).
Совершенно элементарное доказательство этой теоремы имеется во многих книгах; в частности, его можно найти во втором томе трехтомника Кнута. Чтобы сократить доказательство, можно также заметить, что критерий Люка основан на малой теореме
Ферма для чисел из полей Q(√5) или Q(v3). Тест Люка позволил проверить вручную все простые числа до МР7. Когда для проверки простоты стали применяться ЭВМ,
началась настоящая гонка. Очередные новые простые числа Мерсенна рассматривались как свидетельство быстрого роста возможностей ЭВМ. Чтобы убедиться, что Л/819] является составным, Д. Дж. Уилер потратил около 100 часов машинного времени
ILLIAC I — самой быстрой ЭВМ выпуска пятидесятых годов. Гурвицу на IBM 7090 для этой же цели потребовалось лишь 5 часов в 1962 году. В 1964 году Гиллис сделал это на ILLIAC II за 49 минут. А в 1971 году Такерман потратил на это только 3 минуты на IBM 360/91. (Но то были суперЭВМ, а я на своем весьма слабеньком ПК на это потратил 4,125 секунды.) Проверка простоты М1тз на ILLIAC II заняла 2 часа 15 минут, и всего лишь 8 минут на IBM 360/91. (Но это столько нужно суперЭВМ, а моему старенькому ПК нужно всего лишь 9,672 секунды.) Найденное очередное простое число Мерсенна становилось визиткой фирмы. Например, доказательству простоты числа
М112,з Иллинойский университет посвятил выпуск фирменного конверта. IBM в долгу не осталась: она выпустила конверт, посвященный доказательству простоты М19937 (это 6002-значное число, найденное Б. Такерманом 4 марта 1971 года, довольно долго было рекордсменом). Проверка простоты этого числа и у меня заняла изрядное время -
42 094 секунды. с помощью функций Mod и powerMod несложно запрограммировать тест Люка-
Лемера. Сначала дадим нужные определения.
Mn[n_]:=Module[{t=4}, Do[t=Mod [PowerMod[t, 2,mn] -2,mn],<i,
n}]; t];
MPrime[p_]:=Mn[p-2,Mn[p]]==0;
Поскольку единственным простым числом Мерсенна Мр с четным индексом р является Я,, можем ограничиться поиском только нечетных индексов р. (Конечно, программа при этом пропустит число Мг = 3, но разве мы можем о нем забыть?) Вот нужная нам программа поиска нечетных индексов р простых чисел Мерсенна М „.
Block[{p=3}, While [p<45000, {If[MPrime[р],Print[p]], p=NextPrime[p] } ] ]
Даже на весьма слабеньком компьютере всего за несколько часов вы можете найти все нечетные индексы р первых 24 простых чисел Мерсенна известных до 1980 года: 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937. Здесь, конечно, только 23 числа, поскольку индекс первого простого числа Мерсенна М2 = 3 четный: р = 2.
Надеюсь, вы о нем не забыли, так что не забудьте и отпечатать специальные конверт. Заметьте что данную программу очень легко распараллелить и организовать поиск на нескольких ЭВМ. Кроме того, данную программу легко модифицировать так, чтобы поиск продолжался после уже проверенных чисел. Впрочем, возможно, программу придется модифицировать так, чтобы она время от времени подавала признаки жизни", даже если не успевает найти простое число Мерсенна. Это можно сделать, например, так.
Block[{р=19937,1=1},p;
While [p<45000,
{If [MPrime [p],
Print [p]],
p=NextPnme [p] , If[Mod[i++,500]==0,
Print["***p=",p]] HI
Так что если не поленитесь потратить ночку-другую на вычисления, то найдете и другие простые числа р, при которых р-е число Мерсенна Mf = 2'-l является простым. В частности, вы сможете найти 6533-значное простое число Мерсенна Л/,,70, (найдено калифорнийскими школьниками Никкелом и Ноллом в 1978 году), 6987-значное простое число Мерсенна М23209 (найдено Ноллом), 13395-значное простое число Мерсенна Мш„ (это 27-е простое число Мерсенна найдено Д. Словинским в 1979 году), 25962-значное простое число Мерсенна М86243 (это число Мерсенна найдено Дэвидом Словинским в январе 1983 года). Если хотите, проверьте, не пропустил ли я чего-нибудь и сможете ли вы продвинуться дальше. У меня проверка простоты М,1701 заняла 53,547 секунды, М2Ш) - 64,25 секунды, Мшу, - 350,562 секунды (ого, почти 6 минут!), Мим - 1845,34 секунды (это чуть больше получаса). Думаю, что дальнейшее продвижение по данной программе весьма затруднительно. В данном случае либо нужен компьютер со значительно более высоким быстродействием, либо нужно изменить программу так, чтобы большинство составных чисел отсеивалось еще до применения критерия Люка. Казалось бы, перед применением критерия Люка можно проверить, что число Мр не удовлетворяет сравнению ам' = a(modMp) при некоторых а. В качестве а удобно взять, например, число 3. Можно было бы также попытаться проверить другое свойство простых чисел. Однако при этом нужно тщательно следить за тем, чтобы все эти дополнительные проверки не снижали быстродействие программы. Время проверки сравнения an s=a(modMp) может оказаться, например, примерно равным времени проверки по критерию Люка—Лемера. Тогда, понятно, такая дополнительная проверка только замедляет выполнение программы. Так что дальнейшее продвижение требует изобретательности.
Дальше идет степень 110503. В 1983 году была найдена степень 132049, а в 1984 — 216 091. Поиском степеней на суперкомпьютерах прославился в 90-х годах XX столетия Дэвид Словинский. Вместе с Полем Гейджем он получил следующие индексы простых чисел Мерсенна: 756 839, 859 433, 1 257 787. Но степени 1 398 269 и 2 976 221 были найдены Жоэлем Арменгодом (Joel Armengaud) и Гордоном Спенсом (Gordon Spence) на персональных компьютерах по программе, разработанной Георгом Вольтманом (George Woltman) в 1996 году. Предварительная проверка Л/2,76,,, на компьютере с процессором Pentium с тактовой частотой 100 МГц заняла 15 суток в августе 1998 года! 27 января 1998 года Роланд Кларксон (Roland Clarkson) обнаружил простоту Л/3021377, а 1 июня 1999 года Найян Хьяратвала (Nayan Hayratwala) — простоту Af6972593. Впрочем, люди стремятся к рекордам, и после 1983 года числа проверялись не подряд, так что могли что-то и пропустить! Правда, добровольцы тщательно потом все просмотрели до миллиона!
Как из этого видно, критерий Люка—Лемера применяется только после некоторого предварительного отбора, которому уделяется огромное внимание. Давайте попробуем найти хотя бы какой-нибудь очень простой (а, значит, и довольно грубый) метод отсева показателей р, для которых числа Мерсенна Мр не являются простыми. Пусть s— показатель 2 по некоторому простому модулю q: Т =1 (mod q). (Такое 5 можно найти с помощью функции MultiplicativeOrder [2, q].) Поскольку Мp = 1n -1 оно делится на простое число q, если р является показателем 2 по простому модулю q. Так что такие индексы р чисел Мерсенна можно отсеять сразу, если Мр # q. Поэтому для предварительного отсева нам понадобится таблица показателей 2 по простым модулям q. Причем, чтобы уменьшить таблицу, из нее можно вычеркнуть все составные показатели. Чтобы построить таблицу, нам понадобится следующая функция.
f[n_]:=
Block[{q= Prime[n],
s=MultiplicativeOrder[2,q]},
If[NumberQ[s],If[PrimeQfs],s]]]
Эта функция по заданному номеру n находит простое число q = рn, а затем — 5 (показатель 2 по найденному простому модулю q, если он существует). Если оказывается, что показатель 2 по простому модулю q существует, проверяется, является ли он простым числом. Если оказывается, что найденный показатель 2 по простому модулю q является простым числом, он возвращается в качестве значения функции. (В противном случае функция возвращает Null.) С помощью этой функции легко строится нужная нам таблица простых показателей 2 по простым модулям q.
t=Union[Sort[DeleteCasestArray[£,100000, 4] ,Null]]] ;
Функция Array [f, 100000, 4] генерирует следующий список из 100000 элементов {f[4], f[5],...}- Функция DeleteCases [Array [f ,100000, 4] ,Null] удаляет из него элементы, равные Null. Затем функция Sort сортирует этот список, а функцияUnion рассматривает его как множество и тем самым исключает из него повторяющиеся элементы.
Из массива, который первоначально содержал сто элементов, получается список всего из 15 элементов.
tl=Union[Sort[DeleteCases[Array[f,100,4],Null]]]
{3,5,7,11,23,29,37,43,73,83,131,179,191,239,251}
Понятно, что это очень мало. Но даже если бы мы исходили из тысячи простых чисел, у нас бы получился список из 80 элементов.
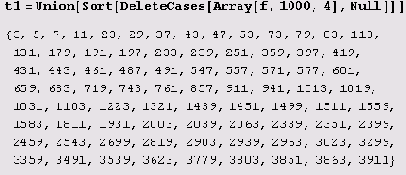
Если же взять сто тысяч простых чисел, получится список из 4536 элементов. Конечно, это тоже не очень много. Кроме того, не все элементы этого списка годятся для отсеивания. Не годятся, например, р = 3, 5, 7. Ведь если простое число р попало в нашу таблицу, это означает лишь, что М р делится на некоторое простое число, возможно на себя, — и тогда оно является простым числом! Поэтому для отсеивания пригодны лишь те элементы нашей таблицы, для которых Л/ больше самого большого простого модуля q, использованного для построения нашей таблицы. Правда, число Мерсенна Мр растет гораздо быстрее, чем л-е простое число рп. Поэтому для большинства элементов из полученного списка выполняется неравенство Мр >q, где q — самый большой простой модуль, использованный для построения нашей таблицы. Однако проблема заключается в том, что в нашей таблице слишком мало чисел. Даже если для построения таблицы мы используем миллион простых чисел, таблица будет содержать всего лишь 37330 чисел. Это значит, что с помощью такой таблицы мы сможем отбраковать менее 4% чисел. Соответственно, и быстродействие программы мы повысим менее, чем на 4 %. Так что в данном случае усложнение программы не оправдано, потому что для большинства чисел (более 96%) будет применяться критерий Люка-Лемера.
Но оказывается, эффективные критерии простоты существуют не только для чисел Мерсенна! Эффективные критерии существуют, например, и для чисел вида k-2n +1.