Алгебра и пакет Mathematica 5
Простые числа вида k*2n +1
Для чисел вида k*2n+1 существует весьма эффективный критерий простоты. Он состоит в проверке сравнения а2n-1 =-1 (mod k*2n +1) для некоторого а. Однако выбор этого а зависит от k. Оказывается, нужно различать случаи, когда k не делится на 3 и делится на 3. Случай, когда k не делится на 3, совсем прост.
Случай, когда k не делится на 3
Если k не делится на 3, то, как заметил Прот (Proth) в 1878 году, числа k*2n +1 являются простыми при kn + 1 тогда и только тогда, когда 32n-1-1 (mod k-2n+l). Впрочем, эта традиционная формулировка критерия Прота несколько некорректна. В ней, например, (молчаливо!) исключается случай n = 1, k = 1. Для n =1, k - 1 имеем k = k3 = 2+1= 2" + 1, хотя З2""* =3sO (mod /n2n+1), причем *-2"+1 =3-простое число. Дело в том, что если число k-2n +1 простое, то в традиционной формулировке критерия Прота число3 должно быть квадратичным невычетом по модулю k-2n + l. Но при и= 1, k= 1 число k2n+l =3. Впрочем, n- 1, k- 1 — единственное решение уравнения k* 2n +1 =3 в целых числах, отличных от 0. (Уравнение k-2" + 1 =3 в целых числах имеет всего два решения: указанное только что решение n= 1, k= 1 и n = 0, k= 2.)
Разыскивая простые числа вида k*2n +1,
конечно, нельзя ограничить перебор по и только простыми числами, но все равно многие значения отсеиваются тривиальным образом.
Пример 7.7. Простые числа вида 5-2n + 1. Рассмотрим, например, случай k = 5. Тогда числа вида 5*2n +1 делятся на 3 при четных п. Так что перебор можем вести только по нечетным и.
Используя функцию PowerMod, очень легко запрограммировать критерий простоты.
MknPrime[k_,n_]:=Module[{t = k*2An+l},
If[k<=2An+l,PowerMod[3,(t-1)/2,t]==t-l,PrimeQ[t]]]
А вот и программа для перебора по нечетным п.
Mkn[k_,nl_]:=Block[{n=l},
While [n<=nl, {If[MknPrime[k,n],Print[п]], n+=2}]];
Теперь можем выполнить перебор. Mkn[5,300000]
Так можно получить (если хватит терпения) следующие значения я: 1, 3, 7, 13, 15, 25, 39, 55, 75, 85, 127, 1947, 3313, 4687, 5947, 13165, 23473, 26607, 125413, 209787, 240937.
Впрочем, при дневном счете терпение обычно улетучивается после печати числа 13165, если не раньше. Конечно, метод перебора можно усовершенствовать, заметив, что если остаток от деления и на 3 равен 2, то число 5*2n +1 делится на 7. Так что числа, дающие в остатке 2 при делении на 3, можно при переборе пропустить. Можно также пропустить числа, дающие в остатке 1 при делении на 10, поскольку тогда число 5*2n + 1 делится на 11. Можно, конечно, пойти и дальше. Можно, например, взять несколько небольших нечетных простых чисел д, для которых существует решение сравнения 5-2n + 130 (mod q). Пусть s— показатели 2 по модулю q: 2s=1 (mod q). (Такое 5 можно найти с помощью функции MultiplicativeOrder [2, q].) Тогда при всех n^t (mod s) 5*2n + 1 = 0 (mod q). Если q не является числом вида 5*2n +1, все числа nst (mod s) можно опустить при переборе. Если же q является числом вида 5*2n +1, то нужно оставить только то число rmt (mod s), при котором 5*n + 1 = q. Эта идея вполне реализуема, но не слишком ли она усложняет перебор?
Давайте попробуем. Вот функция, которая по заданному номеру я простого числа q находит t — решение сравнения 5* 2n +1 = О (mod q) и i — показатель 2 по модулю q, если такое решение существует.
:[n]:=
51ock[{q= Prime[n],
s=MultiplicativeOrder[2,q],
t=MultiplicativeOrder[2,q,{-PowerMod[5,-I, q]} ] }, If[NumberQft],fs,t}]]
Теперь с помощью этой функции можно сгенерировать таблицу остатков и соответствующих им модулей.

Чтобы в таблице сначала шли меньшие модули 5 (они помогают отбраковать больше кандидатов), таблицу пришлось отсортировать, предварительно вычеркнув из нее элементы NULL, которые соответствуют тем простым модулям q, для которых сравнение 5*2n +1 = 0 (mod q) неразрешимо.
Каждая пара в этой таблице описывает арифметическую профессию из показателей, для которых выполняется некоторое тождественное сравнение. Пусть, например, в таблице имеется пара (s,. t). Она была получена для некоторого простого числа q.
Ее наличие в таблице означает, что 5*2n+1 + 1 = 0 (mod q) для любых натуральных k.
Теперь давайте не будем спешить с написанием программы, а предварительно оценим количество чисел, которые может помочь отбраковать такая таблица. Для этого сначала составим программу, которая подсчитывает количество чисел, отбракованных с помощью таблицы. Для этой программы нам понадобится функция, отбраковывающая заданное число по заданной таблице. Вот код этой функции.
fx[n_,t_]:=
Block!(1= Length[t],i=l,c=(i<=l)}, While[c,
{s,r}=t[[i]];answer=(Mod[n,s]!=r); i + +;
c=(i<=l)&&answer];answer]
Эта функция принимает значение True, если число n не было отсеяно с помощью таблицы t, т.е. если оно подлежит дальнейшему испытанию. Теперь можем составить программу подсчета отбракованных чисел.
prog:=
Block[fnn=200000,Yes=0,No=0, j=l}, While[j<=nn,
If[fx[j,t],Yes++,No++] ; J+-2]; Print ["Yes = ", Yes, "; No=",No] ]'
Конечно, количество отбракованных чисел и время отбраковки зависят от размера таблицы t. Сначала давайте возьмем совсем небольшую таблицу.
t=Sort[DeleteCases [Array [f, 10,4] ,Null].]
{{3,2},{10,1},{11,5},{12,9),(18,11),{20,3},{28,20},{36,31}}
Теперь запускаем программу.
prog//Timing Yes= 27274 ; N0= 72726
{5.188 Second,Null}
Как видите, за 5 секунд удалось отбраковать более 72 % чисел! Давайте попробуем увеличить таблицу.
t=Sort[DeleteCases[Array[f,25,4],Null]]
{{3,2}, {10,1}, {11,5},{12,9},{18,11},{20,3},{23,14},
{28,20},{36,31},{51 ,22},{52,31},{58,23},
{60,8},{66,18},{82,14},{100,26},{106,6}}
Опять считаем процент отбракованных чисел и замеряем время:
prog//Timing Yes= 23152 ; N0= 76848
{6.985 Second,Null}
Время отбраковки возросло менее, чем на 2 секунды, а отбраковали мы почти 77 % чисел! Значит, таблицу стоит увеличить.
t=Sort[DeleteCases[Array[L,100,4],Null]] ;
Опять измеряем время:
prog//Timing Yes = 18329 ;
No= 81671 (14.047 Second,Null}
Как видим, таблицу увеличивать стоило! Время отбраковки, конечно, возросло, притом более чем вдвое, но 14 секунд по сравнению с часами счета роли не играют. Так что увеличение таблицы окупает себя! Увеличиваем таблицу еще.
t=Sort[DeleteCases[Array[f,1000,4],Null]];
Теперь снова измеряем время и процент отбраковки:
prog//Timing Yes=12827;
N0= 87173 {74.172 Second,Null}
Конечно, время возросло: теперь отбраковка занимает более одной минуты. Но проверять по-настоящему придется менее 13 % чисел! Потратив дополнительно на предварительную отбраковку чуть более минуты, мы почти в 8 раз уменьшим количество чисел, которые надо будет проверить на простоту. Оказывается, увеличение таблицы оправдало себя и на этот раз. Поэтому еще раз увеличиваем таблицу.
t=Sort[DeleteCases[Array[f,10000,4],Null]];//Timing
{89.969 Second,Null}
На этот раз сама генерация таблицы занимает более минуты. Но и это время окупается.
prog//Timing Yes= 9821 ; N0= 90179
{527.781 Second,Null)
Количество чисел, которые подлежат проверке на простоту, мы уменьшили более чем в 10 раз! Может быть, стоит увеличить таблицу еще? Ну, на этот раз, во всяком случае, уж точно не в 10 раз. Ведь ждать генерации таблицы несколько часов — занятие весьма неприятное! Поэтому лучше сначала попытаться увеличить таблицу, скажем, в 2,5 раза.
t=Sort[DeleteCases[Array[f,25000,4],Null]]///Timing
{638.234 Second,Null}
На генерацию таблицы понадобилось более десяти с половиной минут. Заметно, что время генерации таблицы растет нелинейно с ростом таблицы. Наверное, пора остановиться. Проверяем:
prog//Timing Yes= 8985 ; N0= 91015
{1201.44 Second,Null}
На отбраковку потрачено более двадцати минут. Это на 9,39063 минут больше, чем в предыдущем случае. Несмотря на все это, дополнительно отбраковать удалось менее одного процента чисел. Действительно, пора остановиться. (Надо признать, конечно, что это довольно грубый, притом субъективный критерий останова.)
Теперь можем приступить к написанию программы. Пусть ее заголовок (имя и список параметров) будет М5п[п_]. (Параметр n — верхний конец диапазона, в котором происходит перебор.) Прежде всего нужно решить следующий вопрос: как использовать таблицу так, чтобы не пропустить ни одного простого числа вида 5-2n+1 даже в том случае, если оно использовалось при построении таблицы. Конечно, можно заблаговременно составить список n для таких чисел. Но это значит, что список п для таких чисел нужно составить по другой программе, решающей фактически ту же задачу, решением которой мы сейчас как раз и заняты. При решении этой вспомогательной задачи, правда, можно ограничиться перебором на меньших начальных отрезках натурального ряда. Конечно, этот способ решения вполне корректен. Но такой способ ведет к программе, которая выглядит несколько искусственно. Фактически получится не программа, а подглядывание в раздел ответов в случае небольших значений п. Ничего плохого в этом нет. Просто этот способ реализовать нельзя, если мы не знаем нужную нам часть ответа для решаемой задачи. Поэтому поступим иначе. Мы вообще сделаем вид, что не знаем даже начальных значений п. Сначала в программе найдем все те начальные значения n, при которых числа вида 5*2n+1не превосходят тех простых чисел q, которые использовались для построения таблицы. Хотя это и будет чистый перебор, перебирать придется недолго, поскольку числа вида 5*2n +1 с ростом и растут гораздо быстрее, чем и-е простое число рn. Например, если мы будем строить таблицу, используя первые 25 000 простых чисел, то перебирать без дополнительной отбраковки придется лишь первый десяток нечетных значений п. Затем можно будет построить таблицу и запустить процесс предварительной отбраковки. Поскольку проверка малых значений выполняется весьма быстро, о времени ее выполнения можно не беспокоиться. Может возникнуть и противоположный вопрос» не слишком ли рано мы запускаем отбраковку? Но мы видели, что даже отбраковка 100 000 нечетных чисел с помощью огромной таблицы, построенной с использованием первых 25 000 простых чисел, занимает всего лишь чуть более 20 минут. Так что на предварительную отбраковку одного числа требуется совсем немного времени. Ну а выигрыш отбраковка дает уже при весьма малых значениях и. Поэтому не стоит беспокоиться из-за того, что на некотором, весьма малом отрезке отбраковка может оказаться менее эффективной, чем прямая проверка. Для таблицы, построенной с использованием первых 25 000 простых чисел, перерасход времени, например, не превысит 12 секунд. Так что беспокойство по поводу того, что временные затраты на отбраковку малых значений и могут быть больше, чем на прямую проверку, необоснованно. Но перед запуском отбраковки нужно сгенерировать таблицу t. Даже если таблица строится с использованием первых 10 000 простых чисел, генерация таблицы занимает более минуты. Хотя это время (и даже большее) окупается, поведение программы из-за временных затрат на построение таблицы может показаться несколько неожиданным. Действительно, сначала очень быстро печатаются первые значения п, затем происходит весьма заметная (но необъяснимая, если не знать причину) задержка из-за генерации таблицы, после чего опять довольно быстро печатается следующая серия небольших значений и и лишь затем (на моем компьютере после и = 5947) опять происходит весьма существенная задержка. Она связана как с отсутствием искомых значений я вплоть до n= 13165, так и с тем, что для части чисел (менее 10 %) приходится выполнять полную проверку, которая теперь уже требует весьма ощутимых временных затрат. В приведенной ниже программе учтено все, о чем говорилось выше.
М5n[n_]:=
Block[{j=l,nnprime=25000,primen=Prime[nnprime],nn=Min[n,primen]},
While [5*2Aj+l<=primen&& j<=n,{If[MknPrime[5,j],Print[j]],j+=2}];
If[j<n,
t=Sort[DeleteCases[Array[f,nnprime,4],Null]];While!j<=nn,
If[fx[j,t],If[MknPrime[5,j],Print[j]]]; j+=2]]]
Эта программа существенно быстрее первоначальной, и даже за короткую летнюю ночь она сможет на весьма слабеньком ПК (по нынешним представлениям, конечно) найти n = 26607.
Ну и, наконец, мораль этой истории. Хотя поначалу казалось, что предварительная отбраковка сильно усложнит программу, оказалось, что в системе Mathematica есть все необходимые функции для того, чтобы компактно записать построение необходимой таблицы и тем самым ускорить выполнение программы более чем в 10 раз!
Случай k = 3
Критерий простоты чисел вида 3*2n + 1 несколько сложнее. Впрочем, вся сложность заключается в выборе основания а, для которого проверяется сравнение аm =-1(mod k2n +1). Если и не делится на 4, то в качестве а достаточно взять 5. Иными словами, если п не делится на 4, то 3*2n+ 1 будет простым тогда и только тогда, когда 52"~'* з-1 (mod £-2"+1).
Вот как можно реализовать этот способ. Сначала определим вспомогательную функцию:
MMkn[k_, n_]: = k*2An+l
Теперь запишем критерий простоты.
MMSnPrimeOl[n_]:= Module[{t=3*2^n+1},
If[Mod[n,4]!=0,PowerMod[5,(t-1)/2,t]==t-l,PrimeQ[t]]]
После этого можем написать программу поиска тех и, при которых число 3*2n +1 является простым.
ММ3n[n_]:=
Block[{i=l}, While [i<=n, {If[MM3nPrime01[i],Print[i]], i++}]];
Конечно, данная программа работает существенно быстрее, чем написанная нами ранее для той же цели. Но все же давайте попробуем применить предварительный отсев.
Конечно, метод перебора можно усовершенствовать, если найти арифметическую прогрессию таких показателей п, для которых число 3*2n+1 делится на некоторое простое число д. Тогда показатели n, являющиеся членами этой прогрессии, при переборе можно пропустить, если 3*2n+1< q. Иными словами, можно пропустить те показатели п из этой прогрессии, для которых число 3*2n+1>q. Можно, конечно, пойти и дальше. Можно, например, взять несколько небольших нечетных простых чисел <?, для которых существует решение сравнения 3*2n+1^0 (mod q). Пусть s — показатель 2 по модулю q: T=\1(mod q). (Такое s можно найти с помощью функции MultiplicativeOrder [2, q].) Тогда при всех tmt (mod s) число 3-2n +1 = 0 (mod q). Если q не является числом вида 3*2n+1 , все числа и=/ (mod s) можно опустить при переборе. Если же q является числом вида 3*2n +1, то нужно оставить только то число n=t (mod 5), при котором 3-2n +1 — q. Иными словами, мы сможем отбраковать все те показатели п, которые принадлежат хотя бы одной из построенных нами указанным выше способом арифметических прогрессий. Как мы видели на примере чисел вида 5-2n+1, эта идея значительно повышает быстродействие программы и практически не усложняет перебор. Однако в данном случае таблицы получатся, конечно, совсем другие, и потому оптимальные параметры (главный из них — размер таблицы) придется подбирать заново.
Сначала определим функцию, которая по заданному номеру п простого числа q находит t — решение сравнения 3*2n+1^0 (mod q) и 5 — показатель 2 по модулю q, если такое решение существует.
f3[n_]:=
Block!(q= Prime[n],
s=MultiplicativeOrder[2,q],
t=MultiplicativeOrder[2,q,{-PowerMod[3, -l,q]}]},
If[NumberQ[t],fs,t}]]
Теперь с помощью этой функции можно сгенерировать таблицу остатков и соответствующих им модулей.

Чтобы в таблице сначала шли меньшие модули s (они помогают отбраковать больше кандидатов), таблицу пришлось отсортировать, предварительно вычеркнув из нее элементы NULL, которые соответствуют тем простым модулям д, для которых сравнение 3*2n +1 = 0 (mod q) неразрешимо.
Каждая пара в этой таблице описывает арифметическую профессию из показателей, для которых выполняется некоторое тождественное сравнение. Пусть, например, в таблице имеется пара (s, t). Она была получена для некоторого простого числа q. Ее наличие в таблице означает, что 3*2n+1 +1 = 0 (mod q) для любых натуральных k.
Теперь давайте предварительно оценим количество чисел, которые может помочь отбраковать такая таблица. Для этого сначала составим программу, которая подсчитывает количество чисел, отбракованных с помощью таблицы. Для этой программы нам понадобится функция, отбраковывающая заданное число по заданной таблице. Вот код этой функции.
fx[n_,t_]:=
Block[{1= Length[t],i=l,c=(i<=l) }, While[c,
{s,r}=t[[i]]; answer= (Mod [M, s] !=r) ; i++;
c=(i<=l)S&answer]; answer]
Эта функция принимает значение True, если число я не было отсеяно с помощью таблицы t, т.е. если оно подлежит дальнейшему испытанию. Теперь можем составить программу подсчета отбракованных чисел.
prog:=
Block[{nn=l00000,Yes=0,No=0,j=l}, While[j]=nn,
If[fx[j,t],Yes++,No++]; J++1;
Print["Yes=",Yes,"; No=",No]]
Заметьте, что программа отличается от аналогичной программы для чисел вида 5*2n+ 1. Отличие связано с тем, что на этот раз перебор не ограничивается только нечетными показателями. Конечно, как и для чисел вида 5-2n + 1, количество отбракованных чисел и время отбраковки зависят от размера таблицы t. Сначала давайте сгенерируем совсем небольшую таблицу.
t=Sort[DeleteCases[Array[f3,10,3] ,Null]]
{{3,1},{4,3},{10,7},{12,2],{18,14],{28,9),{36,28}}
Теперь запускаем программу.
prog//Timing Yes= 33650 ; N0= 66350
{4.937 Second,Null}
Как видите, менее чем за 5 секунд удалось отбраковать более 66 % чисел! Давайте попробуем увеличить таблицу.
t=Sort[DeleteCases[Array[f3,25,3],Null]]
{{3,1},{4,3},{10,7),{12,2},{18,14),{28,9},{36,28),{39,29},
{48,5},{51,4 2},{52,9},{58,37},{60,24},{66,60},{82,51},{100,81}}
Опять считаем процент отбракованных чисел и замеряем время.
prog//Timing Yes= 25645 ; N0= 74355
{7.188 Second,Null}
Время отбраковки возросло чуть более чем на 2 секунды, а отбраковали мы более 74 % чисел! Значит, таблицу стоит увеличить.
t=Sort[DeleteCases[Array[f3,100,3], Null]];
Опять измеряем время.
prog//Timing Yes = 21055 ; N0= 78945
{14.765 Second,Null}
Как видим, таблицу увеличивать стоило! Время отбраковки, конечно, возросло, притом более чем вдвое, но 15 секунд по сравнению с часами счета роли не играют. Так что увеличение таблицы окупает себя! Увеличиваем таблицу еще.
t=Sort[DeleteCases[Array[f3,1000,3],Null]];
Теперь снова измеряем время и процент отбраковки.
prog//Timing Yes= 15388 ; N0= 84612
{84.64 Second,Null}
Конечно, время возросло: теперь отбраковка занимает более одной минуты. Но проверять по-настоящему придется чуть более 15 % чисел! Потратив дополнительно на предварительную отбраковку немногим более одной минуты, мы почти в 8 раз уменьшим количество чисел, которые надо будет проверить на простоту. Так что увеличение таблицы оправдало себя и на этот раз. Поэтому еще раз увеличиваем таблицу.
t=Sort[DeleteCasestArray[f3,l0000,3],Null]];//Timing
{90.703 Second,Null}
На этот раз сама генерация таблицы занимает более полутора минут. Но и это время окупается.
prog//Timing Yes = 12123 ; N0= 87877
{630.734 Second,Null}
Количество чисел, которые подлежат проверке на простоту, мы уменьшили более чем в 8 раз! Может быть, стоит увеличить таблицу еще? Ну, на этот раз, во всяком случае, уж точно не в 10 раз. Ведь ждать генерации таблицы несколько часов — занятие весьма неприятное! Поэтому лучше сначала попытаться увеличить таблицу, скажем, в 2,5 раза.
t=Sort[DeleteCases[Array!f3,25000,3],Null]];//Timing
{629.781 Second,Null}
На генерацию таблицы понадобилось почти десять с половиной минут. Заметно, что время генерации таблицы растет нелинейно с ростом таблицы. Наверное, нужно проверить, не пора ли остановиться.
prog//Timing Yes= 11129 ; N0= 88871
{1405.2 Second,Null}
На отбраковку потрачено почти двадцать четыре минуты. Это существенно больше, чем в предыдущем случае. Несмотря на это, дополнительно отбраковать удалось чуть более одного процента чисел. Кажется, пора остановиться. (Конечно, это довольно грубый и притом субъективный критерий останова.)
Теперь можем приступить к написанию программы. Пусть ее заголовок (имя и список параметров) будет М3n[n_]. (Параметр n— верхний конец диапазона, в котором происходит перебор.) Прежде всего нужно решить следующий вопрос: как использовать таблицу так, чтобы не пропустить ни одного простого числа вида 3*2n+1 даже в том случае, если оно использовалось при построении таблицы. Конечно, можно заблаговременно составить список n для таких чисел. Но это значит, что список п для таких чисел нужно составить по другой программе, решающей фактически ту же задачу, «решением которой мы сейчас как раз и заняты. При решении этой вспомогательной задачи, правда, можно ограничиться перебором на меньших начальных отрезках натурального ряда. Конечно, этот способ решения вполне корректен. Но он ведет к программе, которая выглядит несколько искусственно. Фактически получится не программа, а подглядывание в раздел ответов в случае небольших значений п. Ничего плохого в этом нет. Просто этот способ реализовать нельзя, если мы не знаем нужную нам часть ответа для решаемой задачи. Поэтому мы поступим иначе. Мы вообще сделаем вид, что не знаем даже начальных значений п. Сначала найдем в программе все те начальные значения n, при которых числа вида 3*2n+1 не превосходят тех простых чисел q, которые использовались для построения таблицы. Хотя это и будет чистый перебор, перебирать придется недолго, поскольку числа вида 3*2n +1 с ростом и растут гораздо быстрее, чем n-е простое число ра. Например, если мы будем строить таблицу, используя первые 25 000 простых чисел, то перебирать без дополнительной отбраковки придется лишь три-четыре десятка значений п. Затем можно будет построить таблицу и запустить процесс предварительной отбраковки. Поскольку проверка малых значений выполняется весьма быстро, о времени ее выполнения можно не беспокоиться. Конечно, вполне законным является и вопрос: не слишком ли рано мы запускаем отбраковку? Но мы видели, что даже отбраковка 100 000 чисел с помощью огромной таблицы, построенной с использованием первых 25 000 простых чисел, занимает не более 24 минут. Так что на предварительную отбраковку одного числа требуется совсем немного времени. Ну а выигрыш отбраковка дает уже при весьма малых значениях п. Поэтому не стоит беспокоиться из-за того, что на некотором, весьма малом отрезке отбраковка может оказаться менее эффективной, чем прямая проверка. Для таблицы, построенной с использованием первых 25 000 простых чисел, перерасход времени, например, не превысит десятка-двух секунд. Так что беспокойство по поводу того, что временные затраты на отбраковку малых значений n могут быть больше, чем на прямую проверку, необоснованно. Но перед запуском отбраковки нужно сгенерировать таблицу t. Даже если таблица строится с использованием первых 10 000 простых чисел, генерация таблицы занимает немного более полторы минуты. Кроме того, в данной программе есть еще один источник непредсказуемых временных затрат. Это показатели n, кратные 4. Давайте сначала посмотрим, что это будут за показатели. Вот нужная нам программа.
prog401 : =
Block[{nn=8000,Yes=0,No=0,j=4), While[j<=nn,
If[fx[j,t],Print[j,","];Yes++,No++]; j +=4];
Print["Yes=",Yes,"; No=",No]]
В пределах первых восьми тысяч будет найдено 401 число, кратное 4, такое, что его не удастся отсеять с помощью таблицы, для генерации которой использовались 25 000 простых чисел. (Отсеяно будет 1599 чисел.) Далее приведен список тех чисел, которые кратны 4 и выдерживают отсев.
Если показатель я равен одному из этих чисел, то наименьший делитель числа 3*2n+ 1, больший единицы, больше наибольшего простого модуля, использованного для составления таблицы. Вот примеры.
Factor-Integer [3*2АЗб+1]
{(206158430209,1}} Factorlnteger[3*2Л92+1]
{{1132314641089,1},{13119392730926401,1}} Factorlnteger[3*2л96+1]
{{392840481939253,1},{605040718740253,1}} Factorlnteger [3*2лЮ8+1]
{{805213,1},{1781311693519,1},{678750386188027,1}}
Таким образом, нетривиальные делители чисел 3*2n +1, показатели которых выдержали отсев, довольно велики. (Ведь если число 3*2n +1 делится на простой модуль, использованный при построении таблицы, то показатель не выдержал отсев.) Поэтому при применении функции PrimeQ могут произойти временные задержки. Давайте сосчитаем количество таких показателей в пределах первых 300 000. Вот нужная нам программа.
prog4:=
Block[{nn=30000,Yes=0,No=0, j=4}, While[j<=nn,
If[fx[j,t],Yes++,No++]; j+=4];
Print["Yes=",Yes,"; No=",No]]
Вот результаты счета.
prog4//Timing Yes= 14451 ; N0= 60549
{1893.61 Second,Null}
Как видите, в пределах первых 300000 придется проверить только 14451 число, кратное 4. Правда, отсев остальных чисел при этом у меня занял примерно 1893 секунды, т.е. чуть больше получаса.
Хотя, как и в случае чисел 5*2n +1, время на построение таблицы окупается, поведение программы может показаться несколько неожиданным из-за временных затрат на построение таблицы и возможных временных затрат на вычисление функции PrimeQ в случае показателей, кратных 4. Действительно, сначала очень быстро печатаются первые значения п, а затем после n = 534 (на моем компьютере) происходит весьма существенная задержка. Она связана как с отсутствием искомых значений и вплоть до п = 2 208, так и с тем, что для части чисел (чуть более 11 %) приходится выполнять полную проверку, которая теперь уже требует весьма ощутимых временных затрат, причем зачастую весьма непредсказуемых для показателей п, кратных 4. Затем выдача замедляется, но поведение программы выглядит вполне стабильно, пока не будет напечатан показатель n = 3 912. После этого идет большой перерыв, вплоть до w = 20 909. В приведенной ниже программе учтено все, о чем говорилось выше.
М3n[n_]:=
Block[{j=l, nnprime=25000,primen=Prime[nnprime],nn=Min[n,primen]},
While [MMkn[3,j]<= primen && j<=n,
{If[MM3nPrime01[j],Print[j]], J++H; If[j]<n,
t=Sort[DeleteCases[Array[f3,nnprime, 3] , Null]] ;
While[j]=nn,
If[fx[j,t],
If[MM3nPrime01[j],Print[j]]] ; j++]]]
Эта программа существенно быстрее первоначальной, но если хотите по ней найти n = 20 909, понадобится время и ангельское терпение.
Как видим, предварительная отбраковка и в данном случае значительно повышает эффективность программы. Впрочем, эффективность программы все еще сильно определяется неотсеянными показателями n, кратными 4. Хотелось бы и для них найти такое основание а, чтобы для установления простоты числа 3*2n +1 достаточно было проверить выполнение сравнения ат k =-1 (mod /a2n+l). (Ранее для показателей n, не кратных 4, мы полагали а = 5.)
Но все дело в том, что если показатель п делится на 4, то выбрать основание а несколько сложнее. Если показатель п делится на 4, в качестве основания а можно взять любой квадратичный невычет г по модулю 3 * 2n +1. Поэтому если п делится на 4, то сначала нужно найти (желательно небольшой) квадратичный невычет t по модулю 3*2n+1, а затем проверить, выполняется ли сравнение n2n-1=-1(mod k*2n+l). Но как найти квадратичный вычет? Для этого можно использовать квадратичный закон взаимности.
Если Р>1 n Q>1 — положительные нечетные взаимно простые числа, то
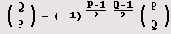
Прежде всего заметим, что если Р — 3*2n +1, то
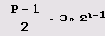
Поэтому
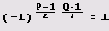
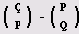
Как видим, для поиска квадратичного невычета r можно использовать функцию JacobiSymbol. В качестве г можно брать небольшие нечетные числа и вычислять для них символ Якоби. (Для квадратичного невычета символ Якоби равен -1.) Как только мы найдем квадратичный невычет r, можем проверить, выполняется ли сравнение r2 k =-1 (mod 32n+l). Теперь легко написать функцию, вычисляющую квадратичный невычет.
ММ3nr[nn_]:= Module[{r=5,
JS=JacobiSymbol[5, nn]}, While[JS!=-1 && r<nn, r+=2; If[GCD[r,nn]= =1,
JS=JacobiSymbol[r,nn]]];r]
Чтобы запрограммировать критерий простоты, воспользуемся функцией PowerMod.
MMSnPrime[n_]:= Module[{t = 3*2^n+1), If[Mod[n,4]!=0,
PowerMod[5,(t-1)/2,t]==t-l,
PowerMod[ММЗnr[t],(t-1)/2,t]==t-l]]
Теперь, наконец, можем написать окончательную версию программы.
M3nv01[n_]:=
Block[{j=l» nnprime=25000,primen=Prime[nnprime],
nn=Min[n,primen]},
While [MMkn[3,j]<= primen && j<=n,
{If[MM3nPrime[j],Print[j]], J++H; If[j<n,
t=Sort[DeleteCases[Array[f3,nnprime,3],Null]]; While[j<=nn,
If[fx[j,t], If[MM3nPrime[j],Print[j]]];j++]]]
Запуская программу с параметром nnprime = 10000 и 25000, убеждаемся, что при этих (и всех промежуточных) значениях генерация таблицы начинается после вывода показателя 12, но до вывода показателя 18. Затем программа довольно быстро добирается до показателя 3912, после вывода которого "уходит в себя" аж до вывода показателя 20 909. (Заметьте, что, в отличие от предыдущей версии программы, перерыв между показателями 534 и 2 208 не слишком заметен — эту "достопримечательность" вы запросто можете пропустить, если выйдете выпить чашечку кофе!)
Оказывается, что число 3*2n+ 1 является простым при n = 1, 2, 5, 6, 8, 12,
18, 30, 36, 41, 66, 189, 201, 209, 276, 353, 408, 438, 534, 2 208, 2 816, 3 168, 3 189, 3 912, 20 909, 34 350,. 42 294, 42 665, 44 685, 48 150, 55 182, 59 973, 80 190, 157 169, 213 321. При всех других n, не превосходящих 300 000, число 3*2n + 1 яляется составным.