Число делителей τ(n)

Давайте подсчитаем число делителей числа 360. Для этого можно просто вычислить длину списка делителей.

Length@Divisors[360]

24 

Есть еще один способ. Можно найти сумму нулевых степеней делителей:

DivisorSigma[0,360]

24 

Числа с заданным числом делителей

Существует единственное натуральное число n = 1, которое имеет только один делитель. Ровно два делителя имеют простые числа, и только они. (Они делятся на 1 и на себя.) Поэтому наименьшим числом, имеющим два делителя, является 2.

А какие числа имеют ровно 3 делителя? Если n = n^mр-... р^m-1 — каноническое разложение искомого числа, то т(л) = (m₁+1) (m₂+1) ... (mt+1). Если τ(n) = 3, то (m1-H) (m2+l) ... (mk+l) = 3. Поскольку 3 — простое число, то слева только один множитель может быть отличен от 1. Поэтому k = 1, а m =2. Поэтому ровно 3 делителя имеют квадраты простых чисел, и только они. Наименьшим числом с 3 делителями является, конечно, 4.

Так же легко найти и все числа, имеющие простое число делителей. Обозначим число делителей через τ(n) = q. Тогда (т,+1) (от2 +1) ... (mt +1) = q. Поскольку q — простое число, то слева только один множитель может быть отличен от 1. Поэтому k=l,aml = q— 1. Поэтому простое число делителей имеют степени простых чисел, и только в том случае, если показатель степени на 1 меньше простого числа. Наименьшим числом с простым числом делителей q является 2^m1.



Теперь давайте найдем все числа, имеющие 4 делителя. В этом случае m(n) = 4 и (m,+l) (m,+l) ... (mt+l) = 4. Поэтому k<2. Если k= 1, то оm1 = 3, а если k = 2, то nm = 0m= 2. Поэтому ровно 4 делителя имеют кубы простых чисел и произведения двух различных простых чисел. Наименьшим числом с 4 делителями является, конечно, 6.

Наконец, давайте найдем все числа, имеющие 6 делителей. В этом случае m(n) = 6 и (оm,+1) (m, +1) ... (mt + 1) = 6. Поэтому k<2. Если k = 1, то оm1 = 5, а если k = 2, то оm =2, 1m = 1. Поэтому ровно 6 делителей имеют пятые степени простых чисел и произведения квадратов простых чисел на другое простое число. Наименьшим числом с 6 делителями является, конечно, 12.

В принципе этот метод можно использовать для вычисления наименьших натуральных чисел, имеющих заданное число делителей.

Впрочем, иногда легче отыскать такое число в таблице, указывающей количество делителей для различных чисел. Составить такую таблицу с помощью системы Mathematica не составляет труда.

Do[Print[n, ":",DivisorSigma[0,n]],

{n,k=50)]

Но едва ли стоит иметь такую таблицу в напечатанном виде. Ведь в компьютерную эпоху поиск путем визуального просмотра нескольких сот страниц справедливо считается не наиболее легким решением. Проще модифицировать программу.

Пример 8.5. Наименьшее число, имеющее 14 делителей. Предположим, нужно найти наименьшее число, имеющее 14 делителей. Тогда программу можно модифицировать так.

m=14;

n=1;

While[DivisorSigma[0,n]!=m,n++];

Print[n, ":", DivisorSigma[0,n]] 

Выполнив эту программу, получим результат.

192 : 14 

Пример 8.6. Наименьшее число, имеющее 100 делителей. Предположим, нужно найти наименьшее число, имеющее 100 делителей. Тогда нужно выполнить следующую программу.

m=100;

n=1;

While[DivisorSigma[0,n]!=m,n++];

Print[n,":",DivisorSigma[0,n]] 

Выполнив эту программу, получим результат.

45360 : 100 

Честно говоря, здесь было немного риска. Ведь если бы числа с заданным числом делителей не оказалось, программа бы зациклилась. Но фокус в том, что всегда существует число, имеющее любое (натуральное, конечно) наперед заданное количество делителей.

Давайте, например, найдем все натуральные числа, количество делителей которых является произведением двух простых натуральных чисел.

Итак, пусть число делителей равно r s, где r и s — простые числа. Тогда n= р^n-1 или n = p^r-v > где p и n — произвольные простые числа.

Но, тем не менее, иногда программа, подобная приведенным выше, работает слишком долго. С ее помощью не удастся, например, за приемлемое время найти наименьшее число, имеющее миллион делителей.

Пример 8.7. Наименьшее число, имеющее миллион делителей. Известный немецкий популяризатор математики Вальтер Литцман в середине XX столетия писал, что согласно математическому бюллетеню Буэнос-Айреса в работе Мерсенна Cogitaeta physico-matematica, изданной в Париже в 1644 году, было указано, что наименьшее число, имеющее миллион делителей, есть

n=126765060022822940149670320537666-8472886094434.

Однако Вальтер Литцман заметил, что некоторые усомнились в этом и послали вопрос в Bolletino di Matematica (4-я серия, т. II, с. 28), было ли доказано это утверждение. Опять же, как сообщает Вальтер Литцман, ответ не был получен.

Давайте хотя бы частично проверим утверждение, сделанное в математическом бюллетене Буэнос-Айреса. Конечно, система Mathematica не может нам помочь проверить, действительно ли Мерсенн, а не кто-то другой нашел это число. Точно так же она не может нам помочь проверить, действительно ли в 1644 году, а не в каком-то другом было сделано это сообщение. Но зато система Mathematica может помочь при подсчете делителей этого числа.

nl=1267650600228229401496703205376;

n2=n!А66;

n3=847288609443; n4=n3А4; n5=n2*n4;

>DivisorSigma[0,п5] 666701

Как видите, миллионом здесь и не пахнет! Так что сомнения были не напрасными. Но опять же Вальтер Литцман указывает, что это число является 2028-значным. Это легко проверить.

Как бы не так! Тут аж 2035 цифр! Возможно, где-то прокралась опечатка. Но где? Вальтер Литцман указывает также, что число nl имеет 100 делителей. Проверим это.

DivisorSigma[0,nl]

101 

Не волнуйтесь, с числом n1 все в порядке. Вальтер Литцман по традиции, восходящей к древним грекам, не учитывает при подсчете делителей само число. В отсутствии опечатки в числе легко убедиться.

FactorInteger [n1]

{{2,100}} 

Да это же сотая степень двойки! А что за зверь является основанием второго сомножителя? Не степень ли числа 3? Проверяем.

FactorInteger[n3]

{{3,25}} 

Так и есть! Теперь мы можем предположить, что Мерсенн указал число видаn-y. Чтобы найти х и у, достаточно решить уравнение (х+1)(у+1)-1 = 1000000 в натуральных числах. Приведем это уравнение к виду (х+1)ОН-1) = 1000001. Найдем каноническое разложение числа 1000001.

Factorlnteger[1000001]

{{101,1),{9901,1})

Как видите, 1000001 = 101x9901. Так что либо х+1 = 101 и у+1 = 9901, либо jc+1 = 9901 и у+1 = 101. Иными словами, либо х - 100 и у = 9900, либо х = 9900 и у- 100. Как видим, вариантов не много. Все зависит от того, какое число меньше: 29900*3100 или 2100 - З9900. Конечно, 29900* 3100< 2100*З9900. Это очевидно, и тут Мерсенн ошибиться не мог. Так что х = 9900 и у = 100. Но это значит, что найденное Мерсенном число можно записать так: 29^m-31^m = (2100)"'(323)4. Так что опечатка, оказывается, в показателе степени: вместо 99 там указано 66. Если учесть технологию верстки книг до середины прошлого столетия (текст приходилось набирать в "перевернутом" виде), то нужно признать, что цифры 6 и 9 можно было запросто перепутать. Поэтому такая ошибка вполне вероятна. Давайте теперь проверим, что мы не ошиблись и найденное нами число действительно имеет миллион (не считая самого себя) делителей.

nl=1267650600228229401496703205376;

n2=n1А99;

n3=847288609443;

n4=пЗМ;

Сошлось, как в аптеке! Но беспокоит вот что: найденное нами число больше того, которое было указано Вальтером Литцманом. А указанное им число имело 2035 знаков, хотя он указал, что должно быть всего лишь 2048 цифр. Давайте посмотрим, какое число получилось у нас.

Это число имеет 3028 цифр! Ага, опять опечатка! А вдруг нет? Ведь мы еще не проверили, что найденное нами число наименьшее.

Пусть n = р^m1 ,р^m2...р^mn — каноническое разложение искомого числа, причем в этом разложении простые числа записаны в порядке возрастания. Тогда τ(n) = (m1+1) (m+1)... (m1 + 1).

Так что (m1+l) (m1+l) ... (mt+1) = 101x9901. Поскольку о(и) = (mn + 1) (m1+1) ... (mt +1) не зависит от чисел pi, а только от показателей m1, m2, ..., mt, то наименьшее число и получится тогда, когда мы будем выбирать наименьшие возможные pi, т.е. должно выполняться условие р( = Prime [i]. (Иными словами, мы должны начать с наименьшего простого числа, а затем выбирать их по порядку. Так что pt = 2, 2 = 3 и т.д.) Так как число n - р™'р™...р™' наименьшее, то mi<m2<...mk. (В противном случае мы могли бы уменьшить число, переставив показатели m1 m2 ..., mk, что совершенно не повлияло бы на количество делителей.) Далее, поскольку (m, + 1)х x(m,+l) ... (mt+l) = 101x9901 и все множители в правой части простые, k<2. Если k = 2, то m1 = 2, рr = 3; все возможные варианты в этом случае мы только что исследовали. Если же k= 1, то р, = 2, но зато m = 1000000. Других вариантов в этом случае нет. Но 210СООО° имеет 301030 цифр.

IntegerPart[Log[10,2^1000000] ]

301029

Так что 21000000 > 29900 * 300. Итак, мы доказали, что наименьшим числом, имеющим

миллион (не считая самого числа) делителей, является 29900-3ⁿ10, имеющее 3048 цифр. Как видите, с помощью системы Mathematica мы провели полное исследование математической части сообщения, сделанного Вальтером Литцманом. Что же касается расследования по исторической части сообщения, то здесь я не могу похвастаться особыми успехами. Дело в том, как научный сотрудник, не связанный со спецслужбами, я не смог получить доступ к оригиналам работ Вальтера Литцмана. (Если вы не связаны с этими самыми спецслужбами, то вы хорошо знаете, что сотрудники "самой научной" библиотеки всегда найдут повод отказать вам в выдаче книги, которая, как кажется сотрудникам этих самых служб, может "недостаточно активно" восхвалять существующий строй. А тут зарубежные книги. Тем более популярные. Кто знает, что они там популяризируют?) Поэтому я видел работы Вальтера Литцмана только в переводе. Мне самому приходилось переводить различные книги, и я хорошо знаю, насколько пренебрежительно в некоторых издательствах относятся к словам автора. Особенно в советских. Там больше смотрели как бы чего не вышло, а далеко не за точностью передачи мысли автора и не за отсутствием опечаток в листингах. Опечатки в вышеупомянутом сообщении я обнаружил еще тогда, когда конструировал системы компьютерной алгебры. Но эти опечатки, конечно, я обнаружил в переводе. Вполне вероятно, что они были сделаны при печати перевода. Но ведь если бы в математическом бюллетене Буэнос-Айреса все было напечатано без опечаток, то почему в Bolletino di Matematica был направлен вопрос? В'чем было сомнение? В математических способностях Мерсенна? В энциклопедии Britannica сказано, что Мерсенн действительно публиковал работу Cogitaeta physico-matematica и издана она была в Париже в 1644 году. Там же сказано, что он был хорошо знаком с работами Ренэ Декарта, Блеза Паскаля, Галилео Галилея, Христиана Гюйгенса, Пьера Ферма... В 1635 году он основал (частную) Парижскую Академию Наук (Academic Parisienne), которая затем стала Академией Наук Франции... В чем, собственно, было сомнение? В том, что Мерсенн смог найти разложение 1000001 = 101x9901? При его-то энергии? В том, что Мерсенн знал формулу для числа делителей τ(n) = (m+1) (n +1) ... (mt +1)? Едва ли, без нее даже подсчитать число делителей было бы весьма трудно. Да и формулу для суммы делителей, очень похожую на формулу для количества делителей, вывели Пьер Ферма и Ренэ Декарт. Причем своими изысканиями в области дружественных чисел Пьер Ферма и Ренэ Декарт занимались независимо, хотя и пришли к тем же формулам, что и один из самых выдающихся арабских математиков абу-Хасан Сабит ибн Корра ибн Марван аль-Харани (836—901). Пьер Ферма сообщил Мерсенну о своем открытии правила Сабита в 1636 году (письмо Мерсенну датировано 24 июня), а Ренэ Декарт — в 1638 году (письмо Мерсенну датировано 31 марта), т.е. за 8 и 6 лет до выхода работы Мерсенна Cogitaeta physico-matematica. Так что наиболее вероятным мне кажется, что опечатки все же были не только в переводах или в работах Вальтера Литцмана... Если вспомнить, что в средние века в книгах слова печатались подряд, без пробелов, а математическая символика практически отсутствовала, то вполне вероятной выглядит версия об опечатке в показателе степени...

Пример 8.8. График количества делителей.

Теперь давайте построим график количества делителей. Сначала используем функции Table и DivisorSigma для построения таблицы tl (точнее, списка) количества делителей первых n чисел. tl= Table[DivisorSigma[0,k],{k,1,n=10^3}];

Теперь можем использовать функцию ListPlot для построения графика.

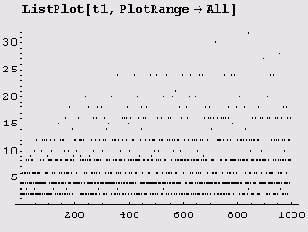
А вот график для n = 100000.

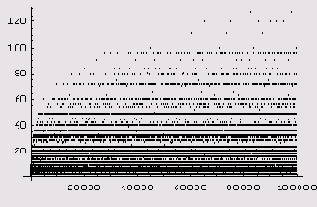
Обратите внимание, несмотря на то что большинство точек расположено весьма невысоко, отдельным точкам удается занять позицию, расположенную выше всех своих предшественников. Абсциссы этих точек являются сверхсоставными числами.

Сверхсоставные числа

Натуральное число и называется сверхсоставным, если у всех натуральных чисел, меньших п, количество делителей меньше, чем у я. Первым сверхсоставным числом является 1 просто потому, что у него нет предшественников. (Парадокс терминологии: 1 является сверхсоставным числом, но не относится к составным. Вторым, конечно, идет 2, третьим — 4, четвертым — 6, пятым — сразу аж 12. Ну а как найти /п-е сверхсоставное число? Вот нужная нам функция.

SuperComposite[m_]:=

Module[{t=l,tmax = l,n=1, n0=l),

While[n<m,{nO++,t = DivisorSigma[0,nO],

If[tmax<t,{tmax=t,n++}]}] ;nO]

Вот как с помощью этой функции можно составить таблицу первых m сверхсоставных чисел.

tl= Table[SuperComposite[k],{k,l,n=m}]

Однако у этой программы есть существенный недостаток: поиск в ней организован весьма неэффективно. Ведь программа для поиска очередного сверхсоставного числа повторяет все вычисления, выполненные для поиска всех предшествующих сверхсоставных чисел. Поэтому она ищет очередное сверхсоставное число слишком медленно. Для составления списка сверхсоставных чисел лучше использовать другую программу.

Module[{t=l,tmax = l,n=l, n0=l, m=10000},

 While[n<m,{n0++,t = DivisorSigma[0,n0],

If[tmax<t,{tmax=t,n++, Print[n, ":", nO]}]}]] 

В составленной по результатам выполнения программы таблице для каждого сверхсоставного числа указано количество и сумма делителей, а также его каноническое разложение.

Заметьте, что в каноническом разложении сверхсоставных чисел простые числа следуют без пропусков (т.е. за Prime [i] в каноническом разложении следует Prime [i+1], а не большее простое число), а показатели степеней — в невозрастающем порядке. Все сверхсоставные числа, за исключением 1, четные. Начиная с четвертого все они делятся еще и на 3 и потому кратны 6. Начиная с пятого все они делятся не только на 2, но и на квадрат двойки, т.е. на 4, и потому кратны 12. Но не думайте, что если n-е сверхсоставное число делится на простое число р, то и все последующие сверхсоставные числа будут делиться на это простое число р. 25-е сверхсоставное число делится на простое число 11, а 26- и 27-е сверхсоставные числа на 11 не делятся. Потом, правда, 11 опять появляется в каноническом разложении. Так что вы, возможно, склонны считать это исключением или аномалией. Но в таком случае придется признать, что это исключение (или аномалия — как вам больше нравится?) не единичное. Ведь 53-е сверхсоставное число делится на простое число 17, а 54-е сверхсоставное число на 17 не делится. В данном случае, правда, аномалия еще короче: 17 появляется в каноническом разложении уже 55-го числа. Как вы думаете, для всякой ли степени данного простого числа найдется такое сверхсоставное число, что все последующие за ним сверхсоставные числа делятся на эту степень данного простого числа? Если вам это очевидно, то заметьте, что из этого немедленно следует, что все сверхсоставные числа, начиная с некоторого, номер которого, конечно, зависит от заданного натурального числа, делятся на это заданное натуральное число. Действительно уж, сверх-составные — антиподы простых! Впрочем, все эти свойства в нашей программе не учитываются. (В программе не учитывается даже, что сверхсоставных чисел бесконечно много.) Зато эту программу легко модифицировать так, чтобы поиск сверхсоставного числа можно было продолжить начиная с любого ранее найденного. Вот как, например, можно продолжить поиск сверхсоставных чисел после 64-го.

Module[{t=l,tmax = 1200,n=64, n0=551350800, m=10000},

While[n<m,{n0++,t = DivisorSigma[0,n0],

If[tmax<t,{tmax=t,n++,Print[n,":", n0]}]}]] 

Тем не менее, нужно заметить, что гораздо более эффективно поиск сверхсоставных чисел можно было бы организовать по их каноническому представлению или же с применением решета, основанного на нахождении чисел, имеющих заданное число делителей. Методы решета позволили бы сразу вычеркнуть из таблицы большинство чисел, поскольку, как мы видели на графике, большинство чисел имеют совсем немного делителей. Ведь при больших n на долю каждого из первых n натуральных чисел в среднем приходится лишь Inn делителей.

Содержание раздела

---

---