Алгебра и пакет Mathematica 5
Графические примитивы
Графические примитивы в графике играют ту же роль, что и основные фигуры в геометрии. Именно из них составляются все остальные фигуры.
Многоугольник — примитив Polygon
Графический примитив Polygon! {{х1, y1], (х2, у2}, ...}]
представляет собой закрашенный многоугольник, ограниченный замкнутой ломаной линий, проходящей через точки
{х1, y1}, {х2, у2), .... Вот как рисуется равносторонний треугольник салатного цвета.

Прямоугольник — примитив Rectangle
Частный случай многоугольника — прямоугольник — можно получить с помощью примитива
Rectangle [{xmin, ymin}, {хmах, уmах} ], в котором
(xmin, ymin} — координаты левого нижнего угла прямоугольника, а {хmах, уmах} - координаты правого верхнего угла прямоугольника. Показанная ниже фигура состоит из пяти прямоугольников. Все они имеют разный цвет.
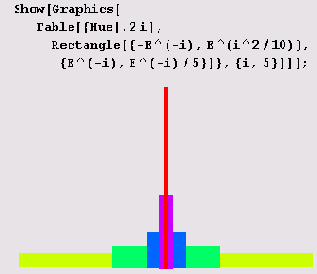
Окружности, эллипсы, их дуги, диски и сектора Окружность и ее дуга — примитив Circle
Дугу окружности создает графический примитив Circlet {х, у},
r, {thl,th2}]. Здесь {х,у} — координаты центра окружности, г — радиус, {thl,th2} — граничные значения полярного угла. Чтобы нарисовать окружность, достаточно вызвать прими- , тив Circlet {х, у}, г]. Ниже представлено произведение искусства, состоящее исключительно из окружностей.

Чтобы было легче разобраться в этом шедевре, скажу, что он состоит из п = 8 семейств малых окружностей, вокруг которых имеется два "обода". Внешний (тонкий) обод — окружность. Внутренний (толстый) обод — семейство концентрических окружностей. Эти два обода как бы служат рамкой для шедевра. Сам шедевр состоит из п = 8 семейств маленьких окружностей, центры которых также лежат на окружности. Теперь, чтобы разобраться в шедевре, достаточно знать значения следующих величин, использованных при его построении:
n = 8 — количество семейств маленьких окружностей;
m= 40 — количество маленьких окружностей в каждом
семействе;
r= 10 — радиус маленьких окружностей;
R = lr — расстояние от
начала координат до наиболее удаленного (от начала координат) конца проведенного
через начало координат диаметра окружности, на которой расположены центры
маленьких окружностей; в программе положено i = 3;
i — номер семейства окружностей; отсчет номера
начинается с 0;
j — номер маленькой окружности в семействе; отсчет номера начинается с 0;
Rtheta[t] — вектор с координатами {Cos[t], Sin[t]};
i*2*Pi/n — угол между осью абсцисс и отрезком, соединяющим начало координат с центром окружности, на которой расположены центры маленьких окружностей i-го семейства;
R*Rtheta[i*2*Pi/n] — координаты наиболее удаленного (от начала координат) конца проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей
i-го семейства;
kr— расстояние от начала координат до ближайшего (к началу координат) конца проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей; в программе положено k = 1;
k*r*Rtheta[i*2*Pi/n] — координаты ближайшего (к началу координат) конца проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей
i-го семейства;
R1 = (R+k*r)/2 — радиус окружности, на которой находятся центры тех окружностей, на которых расположены центры маленьких окружностей семейств;
Rl*Rtheta[i*2*Pi/n] = (R+k*r)*Rtheta[i*2*Pi/n]/2 — координаты середины проведенного через начало координат диаметра окружности, на которой расположены центры маленьких окружностей /-го семейства; иными словами, это центр той окружности, на которой лежат центры окружностей
i-го семейства;
rl = (R-k*r) /2 — радиус окружности, на которой расположены центры маленьких окружностей семейства;
Rl*Rtheta[i*2*Pi/n]+rl*Rtheta [i*2*Pi/n+j/m*Pi] — координаты центра у
окружности i-го семейства.
Здесь умышленно сохранено большое количество параметров, так как это облегчает подбор нужного рисунка. Ниже изменены только два параметра.

На представленном ниже рисунке немного смещен центр окружностей семейства.

На представленной ниже вариации на эту же тему радиус окружности семейства переменный.

Пример 9.1. Колесо со спицами. Примитивов Circle и Line вполне достаточно для изобретения, простите, изображения колеса.
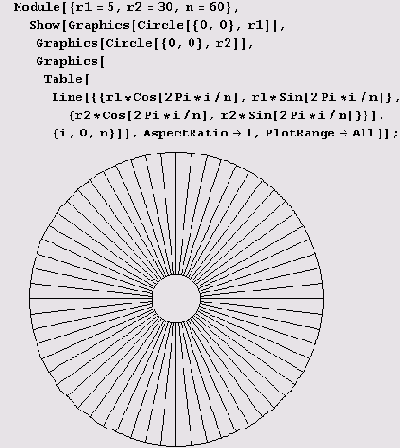
Но не перепутайте синус и косинус, а то получится колесо Эшера.

Эллипс и его дуга — примитив Circle
Дугу эллипса с полуосями rх и rу создает графический примитив
circle [ {х, у], (rх, rу}]- Здесь {х, у] — координаты центра эллипса. Графический примитив
Circle[{х, у], {rх, rу}, {thl, th2}] рисует дугу эллипса, которая получается из соответствующей дуги окружности. Центр эллипса находится в точке с координатами [х, у],
rх и rу — полуоси, a (thl, th2] — граничные значения полярного угла для дуги окружности. Чтобы нарисовать эллипс, достаточно вызвать примитив circle ({x, у], (rх,
rу}]. Ниже нарисован эллипс, окружность, диаметр которой совпадает с меньшей осью эллипса, и дуга окружности.

Пример 9.2. Окружность, вписанная в треугольник. Давайте напишем функцию inscribedcircle, которая по заданному своими вершинами треугольнику вписывает в него окружность. Предварительно нам понадобится функция, назовем ее inscribedCircleData, которая вычисляет радиус и координаты центра окружности, вписанной в треугольник.
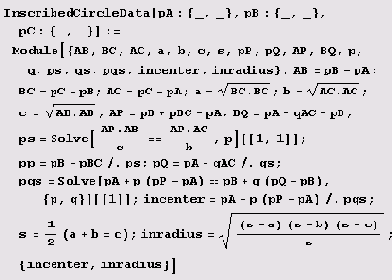
Теперь можем написать функцию, отображающую стороны треугольника и вписанную в него окружность.

(Здесь Sequence превращает Sequence@@InscribedCircleData[pA,pB,pC] в
Sequence [рА,рВ,рС].) Теперь можем приступить к рисованию.
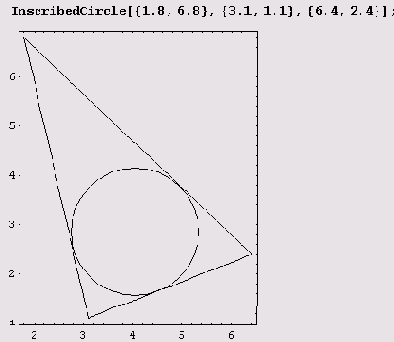
Диски (закрашенные эллипсы, окружности и их сектора) — примитив Disk
Закрашенный диск получается с помощью примитива Disk, параметры которого в точности совпадают с параметрами примитива Circle. В частности, закрашенный круг получается с помощью примитива
Disk[[х, у), r].
Текст
С помощью графического примитива Text [expr, {х, у} ] задается текст.
Здесь ехрr — любое выражение, причем центр печатной формы вычисленного его значения помещается в точку с координатами (х, у]. Предположим, мы нарисовали график параболы у = (2 + х)
^2 на отрезке [-3, -1] и обозначили через р графический объект
р = Plot[ (2+х) ^2, {х,-3,-1}]. Тогда полученный нами рисунок можно снабдить поясняющим текстом.
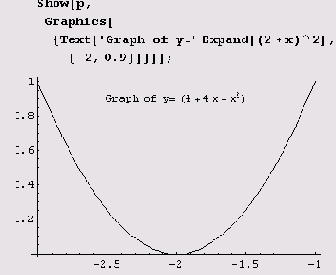
В графическом примитиве Text можно задать еще один параметр — смешение offset Text [expr, coords, offset]. Этот параметр определяет смещение текста. По умолчанию он равен {0, 0}, а это означает, что центр текста должен находиться в точке с координатами
coords. При установке {-1, 0} левый край текста начинается в точке с координатами coords; {l, 0} — правый край текста находится в точке с координатами coords; {0, -1} — текст центрируется выше точки с координатами coords; {0, 1} — текст центрируется ниже точки с координатами coords.
Вот пример использования смещения offset.

Наконец, параметр dir позволяет указать направление чтения текста: Text[ex/w, coords, offset, dir]. Если dir = {1,0}, то текст располагается как обычно, т.е. горизонтально. Если
dir = {0, 1}, то текст размещается вертикально и читается снизу вверх. Если dir = {0,-!}, то текст располагается вертикально и читается сверху вниз. Если
dir = (-1,0), то текст располагается горизонтально, но перевернутым, т.е. "вверх ногами".
Кроме того, добавить текст или другие графические примитивы в рисунки, созданные встроенными графическими функциями, можно с помощью опций
Prolog и Epilog. По умолчанию они равны пустому списку {}. Однако в любой из этих списков можно добавить любые подходящие случаю примитивы. Разница между рассматриваемыми опциями состоит в том, что примитивы опции
Prolog рисуются до основного рисунка, а примитивы опции Epilog — после.
В Приведенном ниже примере до рисования графика функции рисуется окружность.
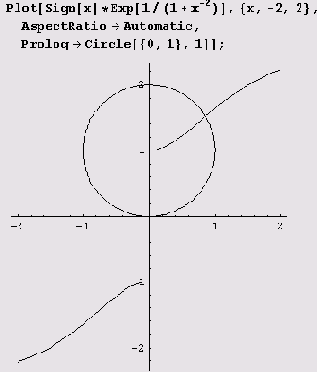
Ниже приведен пример использования опции Prolog вместе с вызовом в графическом примитиве
Text функции FontForm, аргументами которой являются строка с текстом, название и размер шрифта для текста. На рисунке нарисовано два графика — график функции Эйри (решение дифференциального уравнения
уn-ху = 0) и ее производной.
