Вычерчивание графиков

Для вычерчивания графиков функций одной переменной имеется несколько функций. Самой важной из них является, пожалуй, Plot.

Функция Plot

Эта функция уже неоднократно встречалась нам ранее. Количество ее опций просто поражает.

Эта функция позволяет чертить сразу несколько графиков функций. Чтобы начертить сразу несколько графиков функций, в качестве первого аргумента функции Plot задается список функций. Для того чтобы различить графики, обычно используется опция PlotStyle -> {{dirl}, {dir2},...}, где dir1— совокупность графических директив, относящихся к 1-му графику, dir2— совокупность графических директив, относящихся к 2-му графику, и т.д. Ниже вычерчено два графика: парабола — жирной линией и прямая — потоньше. Кроме того, эти графики различаются цветом (на экране, конечно).

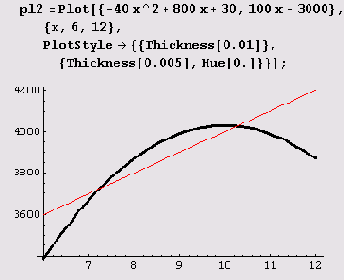
Заметьте, что координатные оси пересекаются на этом рисунке не в начале координат (не в точке с координатами (0, 0)). Однако если установить опцию AxesOrigin-> {xorigin, yorigin}, то оси будут пересекаться в точке с координатами (xorigin, yorigiri).

Рассмотрим пример построения графиков нескольких функций. Пусть функции, графики которых мы хотим построить, получаются с помощью функции Table или NDSolve. Для определенности пусть это будут полиномы Чебышева. Следующая строка ошибочна.

Plot[Table[ChebyshevT[n,x] ,{n,l,4}],{x,-l,l})

Дело в том, что здесь система Mathematica не сможет вычислить функции. Почему? Давайте разберемся. Начнем сначала. Вот график, который строится без проблем.

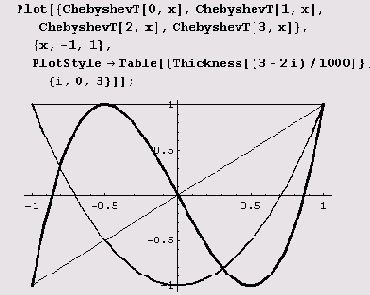
Здесь построены графики первых четырех полиномов Чебышева первого рода: ChebyshevT[0, x] — полином нулевого порядка, равный тождественно единице, ChebyshevT[l,x] = х, а также полиномы ChebyshevT[2,z] и ChebyshevT[3,x]. Но вот так график построить не удастся.

list01={ChebyshevT[0,x],ChebyshevT[1,х],ChebyshevT[2,х],ChebyshevT[3,x]}

{1, х, -1 + 2х2, -Зх + 4х3} Plottlist0l,{х,-1,1}];

Plot::plnr: list0l is not a

machine-size real number at x =-1.. More...

Оказывается, система Mathematica не может вычислить значения list01! Почему? Потому что функция Plot имеет атрибут HoldAll.

Attributes[Plot] {HoldAll,Protected)

Этот атрибут указывает, что аргументы функций вычисляться не должны. Обычно аргументы функций вычисляются.

hh[1+2,2+3,3+4] hh[3,5,7]

Но если функции приписать атрибут HoldAll, вычисления аргументов выполняться не будут.

SetAttributes[hh,HoldAll] hh[l+2,2+3,3+4] hh[l+2,2+3,3+4]

Чтобы в таких случаях выполнить вычисления, можно использовать функцию Evaluate. Выражение Plot [Evaluate [list0l], {x,-l, 1} ]; строит предыдущий график без проблем. Ниже построены графики 8 полиномов Чебышева.

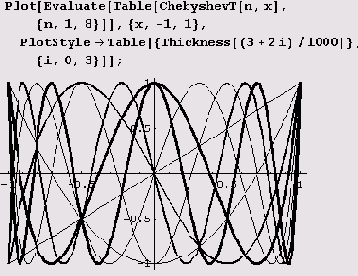
Иногда на рисунке через точки координатных осей с координатными отметками нужно провести сетку вертикальных и горизонтальных прямых. Для этого достаточно установить опцию GridLines равной Automatic.

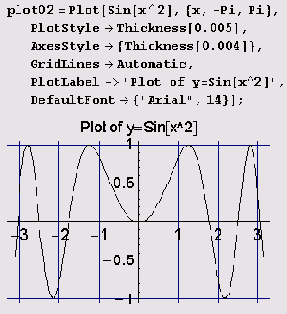
В данном случае сетка видна на графике функции у = sin x², приведенном выше.

Опция PlotStyle задается так же, как и опции AxesStyle и FrameStyle, но определяет графический стиль линий.

При построении графиков система Mathematica использует адаптивный алгоритм, который предусматривает получение достаточно гладких кривых. Одним из критериев гладкости является величина угла между последовательными отрезками, аппроксимирующими график функции между соседними точками, в которых вычисляются ее значения. Величина этого угла устанавливается опцией MaxBend, по умолчанию он равен 10°. Вот график функции у = e-f .

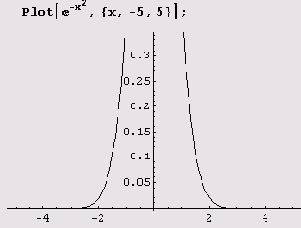
Как видите, график построен не полностью. Причина заключается в том, что вверху мы имеем слишком острый пик. Но если увеличить опцию MaxBend, например, до 15, пик будет нарисован полностью.

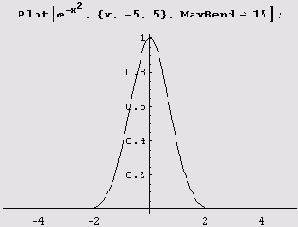
Иногда значение этой опции приходится уменьшать.

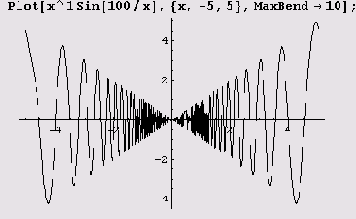
Слева хорошо заметен излом. Этот недостаток легко исправить.

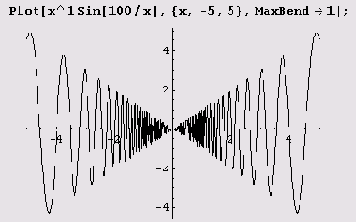
Как видите, несколько изъянов исчезло.

Количество точек, в которых производятся вычисления, регулируется опцией PlotPoints, которая по умолчанию равна 25. Если угол между последовательными сегментами превосходит значение опции MaxBend, то производится дробление интерзала между соседними точками, но таких шагов дробления не может быть больше, чем значение опции PlotDivision. Если это значение мало, график получится угловатым.

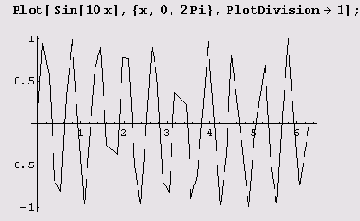
Если же использовать значение по умолчанию (оно больше 1), график будет более гладким.

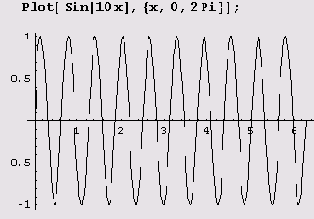
Для уменьшения времени вычисления функций в выбранных по адаптивному алгоритму точках производится их компилирование, заключающееся в создании некоторого псевдокода. Однако это может привести к уменьшению точности вычислений. Чтобы избежать подобной потери точности, нужно применить опцию Compiled->False. Давайте посмотрим, для каких функций по умолчанию установлена опция Compiled->True.

Block[{$Messages={}}, Select[Names["*"],

Options[ToExpression[I],Compiled]=={Compiled->True}&]]

 {ContourPlot,DensityPlot,FindMaximum,FindMinimum,FindRoot,

NDSolve,NIntegrate,NProduct,NSum,ParametricPlot,

 ParametricPlot3D,Play,Plot,Plot3D}

Построение графиков функций, заданных параметрически, — функция ParametricPlot

Функция ParametricPlot позволяет рисовать кривые и семейства кривых, заданных параметрически. Эта функция имеет те же опции, что и функция Plot. В некотором смысле эта функция универсальна. Если не учитывать неявно заданных функций, то именно функция ParametricPlot позволяет построить графики всех мыслимых функций, включая и многозначные. Без проблем строятся и графики, заданные в полярной системе координат. Фигуры Лиссажу, кривые Уатта, овалы Кассини, Декарта, Мюнгера, улитки Паскаля, однолистники, листы Декарта, всевозможные розы и розетки, рулеты, годографы, эволюты и эвольвенты всех мыслимых и немыслимых кривых, циклоиды, всевозможные спирали, циссоиды, конхоиды, строфоиды, астроиды, кардиоиды, неоиды, лемнискаты, узлы, квадратрисы, клотоиды, кохлеоиды, трохоиды, элипсиды, катакаустики, всевозможные параболы, локсодромы и лоциклики, трезубцы, трисектрисы, трилистники, верзиеры, брахистохроны, подэры, кривые с именами древнегреческих и средневековых ученых — вот далеко не полный перечень всевозможного зверья, которое может быть нарисовано функцией ParametricPlot.

Пример 9.3. Фигуры Лиссажу. Это классический пример применения функции ParametricPlot. Рисуются эти фигуры совсем просто, и потому мы нарисуем сразу несколько.

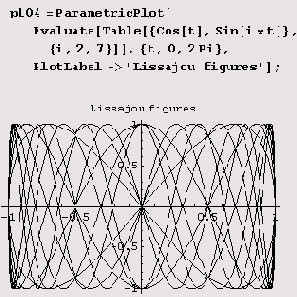
Пример 9.4. Розы и розетки. Эти цветы весьма многочисленны, выглядят, как правило, очень мило и легко рисуются. Процесс вычерчивания совсем прост, если предварительно определить следующую функцию.

PolarR[al,a2_,omega_,phi_]:=Module[{r=al+a2*Cos[omega*phi]},

<r*Coi[phi],r*Sin[phi]}]

Вот как, например, с помощью этой функции рисуется многолепестковая роза.

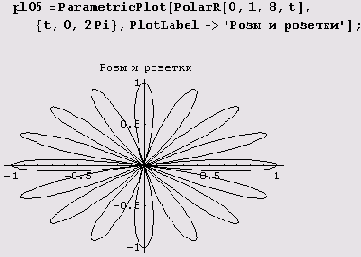
А вот еще один милый цветок.

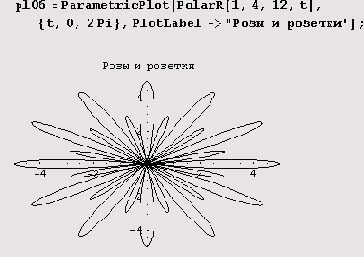
Цветы эти столь разнообразны, что согласия относительно количества их видов нет. Одни насчитывают более полтора десятка видов, другие — не менее сотни.

Пример 9.5. Кривые в полярных координатах. Построение кривых в полярных координатах значительно упрощается, если предварительно определить функцию PolarXY.

PolarXY[r_,phi_]:=

{r*Cos[phi],r*Sin[phi]}

Вот как, например, с помощью этой функции рисуется улитка Паскаля.

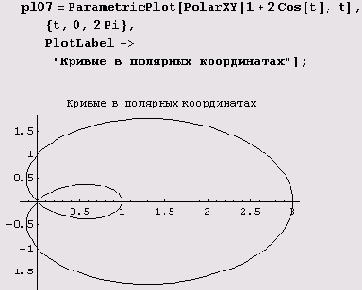
Пример 9.6. Полярные зверинцы. Иногда приходится подбирать параметры в семействе кривых, заданных в полярных координатах. Этот процесс значительно упрощается, если предварительно в определение функции PolarXY ввести параметры, которые определяют кривую семейства.

PolarXYAB[r_,phi_, а_,b_]:=

{r*Cos[a*phi],r*Sin[b*phi]}

Вот как, например, с помощью этой функции рисуется одна из кривых семейства.

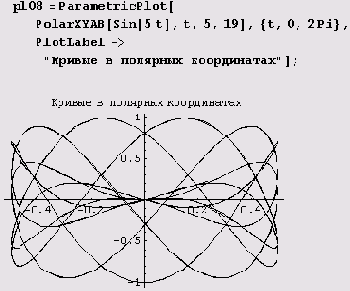
Как вам эта зверушка? Понравилась? Если да, вы подобрали параметры! Если нет, пробуйте другие параметры.

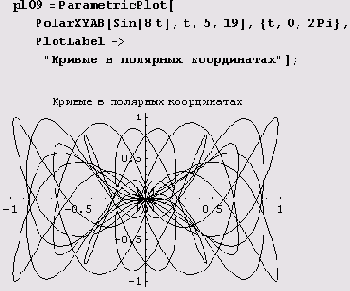
Ну а эта зверушка? Неужели не нравится? Тогда продолжайте перебирать параметры...

Пример 9.7. Годографы. Иногда приходится вычерчивать годографы семейства вектор-функций, заданных в полярных координатах. В определении такой функции часто участвует некий вектор (очень часто единичный), который с течением времени вращается вокруг начала координат. Пусть, например, нужно вычертить годограф вектор-функции r(t) = аte + R^t+a(e) + АR^wt+p(e), где e — единичный вектор, R^ф — поворот на угол ф вокруг начала координат, а а, а, А, w, p — заданные параметры. Тогда, чтобы упростить определение функции PolarXYAB, можно поступить так. Сначала определим следующую функцию.

Rphi[phi_]:={Cos[phi],Sin[phi]}

С ее помощью значительно упрощается определение функции PolarXYAB, которое упрощает задание кривой семейства.

PolarXYAB[t_,a_,alpha_,aa_,omega_,beta_]:=

{0,a*t}+Rphi[t+alpha]+aa*Rphi[omega*t+beta]

Вот как, например, с помощью этой функции рисуется одна из кривых семейства.

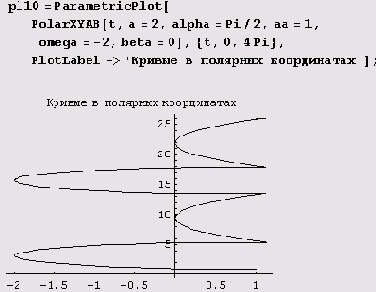
Как вам эта зверушка? Если думаете, что они все такие, вы ошибаетесь.

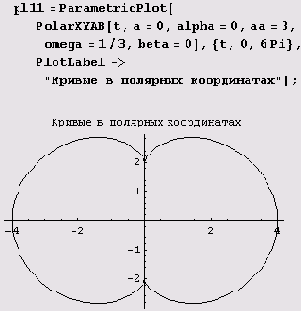
Вращающийся единичный вектор очень часто полезен и при вычерчивании других кривых, например циклоид.

Пример 9.8. Циклоиды. Циклоиды (высших порядков) описываются уравнением Z = l₀+l₁t^iwt+l₂t^iwt+..+l_nt^iwn. Вот как, например, выглядит определение функции PolarXYAB для циклоид некоторого определенного типа.

PolarXYAB[t ,rl_,r2_,a_,omega_]:=

r1+r2*Rphi[t]+a*Rphi[omega*t]

Вот как теперь рисуется одна из циклоид.

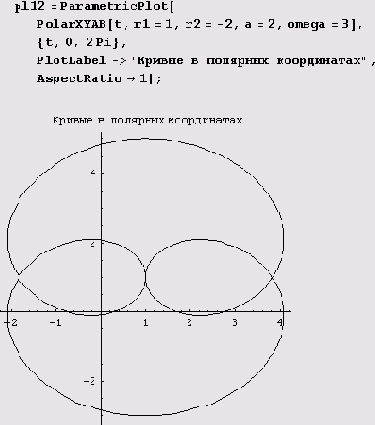
Пример 9.9. Гиперболы в полярных координатах. Введенную нами функцию

PolarXY[r_, phi_] : = { r*Cos [phi], r*sin [phi]} удобно использовать также в определении функции PolarXYAB для многих функций, заданных в полярных координатах. Посмотрим, как это делается на примере вычерчивания полярных гипербол.

Вы знаете, как выглядит полярная гипербола

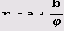
Если нет, вас ждет сюрприз!

Сначала дадим определение функции PolarXYAB для полярных гипербол.

PolarXYAB[t_,a_,b_]:= PolarXY[r=a+ b/t,t]

Вот как теперь рисуется полярная гипербола.

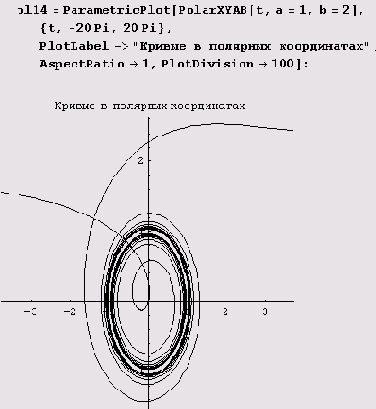
Позвольте вас спросить, а сколько асимптот у полярной гиперболы?!

Пример 9.10. Параболы в полярных координатах. Применим теперь введенную нами функцию PolarXY[r_, phi_] : = {r*Cos [phi], r*sin[phi] } для вычерчивания полярных парабол r= аφ²+bφ+с. Сначала дадим определение функции PolarXYAB для полярных парабол.

PolarXYAB[t_,а_,n ,с_]:=

PolarXY[r=a*t~2+b*t+c,t]

Вот как теперь рисуется полярная парабола.

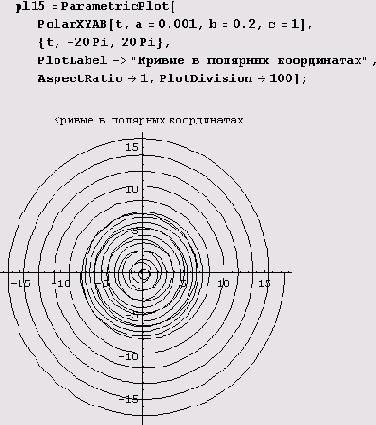
Пример 9.11. Кривые второго порядка в полярных координатах. Ну а сложно ли вычертить в полярных координатах обычную кривую второго порядка? Нисколько. Сначала дадим определение функции PolarXYAB для обычных кривых второго порядка.

PolarXYAB[t_,a_,b_]:=

Pol^rXY[r=l/(a+b*Cos[t]) , t]

В зависимости от параметров у нас получится обычная кривая второго порядка, причем фокус будет находиться в начале координат. Вот как рисуется обычная гипербола.

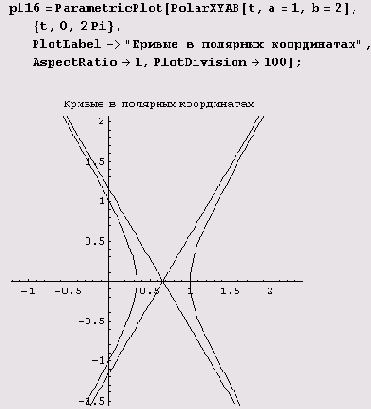
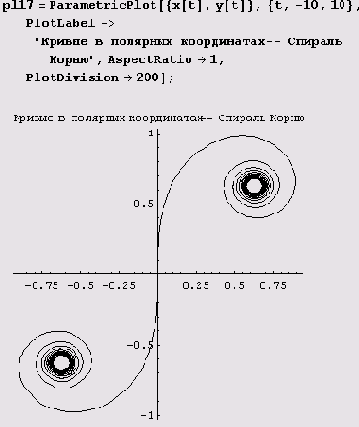
Пример 9.12. Спираль Корню. Предположим, нужно начертить кривую, которая имеет сложные параметрические уравнения х = x(i) и у = y(t). Тогда лучше всего предварительно определить функции х = x(t) и у - y(t) и именно их использовать в функции ParametricPlot. Покажем, как это делается на примере спирали Корню. В соответствии с рекомендацией сначала определяем x(f) и y(f) для спирали Корню.

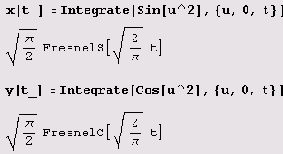
Как видите, система Mathematica заметила, что x(t) и y(f) являются интегралами Френеля. Теперь, определив x(t) и y(t), можем построить график.

Специальные типы графиков

Как мы видели, функция ParametricPlot практически универсальна. Однако часто приходится строить графики специального вида. Тогда можно воспользоваться более специализированными функциями.

Графики в полярной системе координат

Построение графиков в полярной системе координат зачастую упрощается, если воспользоваться функцией PolarPlot из пакета Graphics`Graphics`. Пакет этот загружается как обычно. <<Graphics` Graphics`

Ниже показано, как нарисовать эллипс и улитку на одном графике.

Пример 9.13. Несколько графиков в разных системах координат на одном чертеже.

Иногда на одном листе (чертеже) нужно начертить несколько графиков, притом в разных системах координат. Предположим, на одном листе нужно начертить четыре графика, расположив их в два ряда по два графика, т.е. два графика в верхнем ряду и два — в нижнем. Два графика создадим с помощью функции ParametricPlot, a два — с помощью функции PolarPlot. Сначала загружаем нужный графический пакет.

<<Graphics `Graphics`

А теперь задаем радиус-вектор как функцию угла

Сlearг[r]

г[theta_]=Sin[8 theta/7];

и определяем первый график.

ppl=ParametricPlot[{г[theta]Cos[theta],r[theta]Sin[theta]},

{theta,0,14Pi},AspectRatio->Automatic,DisplayFunction->Identity] ;

После этого точно так же готовим второй график.

Clear[r]

r[theta_]=theta*Cos[ theta];

pp2=ParametricPlot[{r[theta]Cos[theta],r[theta]Sin[theta]},

{theta,-19Pi/2,19Pi/2},AspectRatio->Automatic,PlotPoints->200,

DisplayFunction->Identity];

Аналогично строим третий график, но в полярных координатах с помощью функции PolarPlot.

Clear[r]

r[theta_]=Exp[Cos[ theta]]-2Cos[4theta]+Sin[theta/12]Л5;

pp3=PolarPlot[r[theta],{theta,0,24Pi},AspectRatio->Automatic,

PlotPoints->200,PlotRange->{{-4,5},{-4.5,4.5}},

DisplayFunction->Identity];

Последний, четвертый, график тоже строим в полярных координатах с помощью функции PolarPlot.

Cleart[r]

pp4=PolarPlot[{Sqrt[l/theta],-Sqrt[I/theta]},{theta,0.1,lOPi},

AspectRatio->Automatic,PlotPoints~>200,

PlotRange->All,DisplayFunction->Identity] ;

Наконец, группируем четыре графика в двухмерный массив с помощью функции GraphicsArray и отображаем все четыре графика (полученный массив из двух строк по два графика в строке) с помощью функции show.

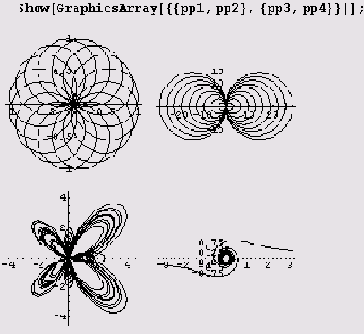
Как видите, все очень просто! Зато сейчас вам предстоит ответить на очень трудный вопрос: какая из функций PolarPlot и ParametricPlot лучше подходит для создания графика функции, заданной в полярных координатах? По собственному опыту могу сказать, что часто ответ очевиден, но иногда легче начертить по сотне графиков с помощью обеих функций, чем обосновать без ссылок на личные предпочтения выбор конкретной функции!

График функции, заданной на дискретном множестве точек, — функция ListPlot

Функция ListPlot предназначена для построения графика функции, заданной на дискретном множестве точек. Поэтому ее первый аргумент является либо списком значений функции (в этом случае считается, что эти значения функция принимает в точках 1, 2, 3, ...), либо списком пар вида [абсцисса, ордината]. Конечно, этот список можно создать и какой-либо функцией, например Table. У этой функции есть одна отличительная особенность: размером точек управляет графическая директива Pointsize, а не Thickness, потому что в данном случае мы имеем точки, а не линии. Впрочем, иногда точки на графике нужно соединить отрезками прямых. Для этого в функции ListPlot нужно установить дополнительную опцию PlotJoined->True. К другим часто используемым опциям относятся AxesOrigin, GridLines и PlotStyle.

Плоские графики функций двух переменных

Казалось бы, плоскость двухмерна, и потому на ней можно рисовать графики только одной переменной. Но, оказывается, что на самом деле, хотя плоскость и плоская, ее можно раскрасить и с помощью цвета отобразить значение функции от двух независимых переменных! До этого давно додумались картографы. Система Mathematica тоже умеет использовать эту возможность. Функции ContourPlot и DensityPlot позволяют графически изображать функции двух независимых переменных. Функция ContourPlot, например, строит линии уровня. Первым аргументом рассматриваемых

функций является выражение, задающее функцию двух переменных. Независимые переменные и области их изменения определяются с помощью двух списков вида [переменная, минимальное_значение, максимальное_значение], следующих за первым аргументом.

Линии уровня

Вы наверняка видели топографические карты какой-нибудь местности и физические карты материков, океанов и островов. И, несомненно, вы не могли не заметить на них линии уровня. Вдоль таких линий высота над уровнем моря постоянна. Если двигаться по таким линиям, высота над уровнем моря не будет изменяться. Но высоту над уровнем моря можно рассматривать как функцию точки. Линии (точнее, множества) точек, на которых функция постоянна, называются линиями уровня, или изолиниями (данной функции). В системе Mathematica есть две функции, предназначенные для вычерчивания графиков с линиями уровня: ContourPlot и ListContourPlot.

Функция ContourPlot

Эта функция вычерчивает графики функций, заданных аналитически. Вот как, например, можно вычертить график функции z — sin xy с линиями уровня.

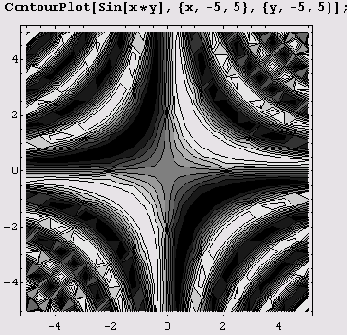
Как видите, это подобно раскраске физической карты. Иногда нужно оставить только линии уровня, а сам график не раскрашивать. Тогда нужно воспользоваться опцией ContourShading->False.

Иногда, наоборот, нужно оставить только раскраску, а изолинии сделать невидимыми. Тогда нужно воспользоваться опцией ContourLines->False.

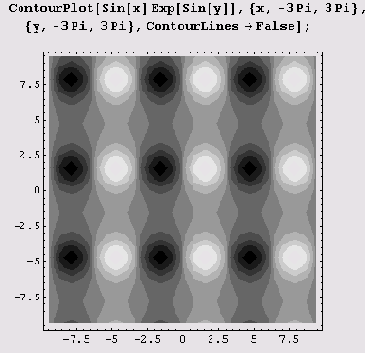
Контурный график можно раскрасить. Для этого нужно воспользоваться опцией ColorFunction->Hue. (По умолчанию установлено ColorFunction->Automatic, что приводит к раскраске оттенками серого.) В случае опции ColorFunction->Automatic области с меньшими значениями функции имеют более темные оттенки серого цвета, чем области с большими значениями функции. Иногда нужно подобрать цвета. Тогда придется поэкспериментировать с этой опцией. Можно, например, установить ColorFunction->(Hue[l-t]&), ColorFunction->(Hue[Abs[0.5-i]]&) или ColorFunction-> (Hue [1-Sin [Pi (l-#) ] ] &). По возможности можете руководствоваться правилами цветового дизайна, я же советов давать не буду, поскольку, как известно, на вкус и на цвет товарища нет...

Как быть, если нужно отображать только изолинии, соответствующие заранее заданному количеству уровней, или только изолинии заданных уровней? Нет проблем! Для этого есть опция Contours. По умолчанию число линий уровня на рисунке равно десяти, но если установить Contours->1 то будут отображаться только изолинии и уровней, равномерно распределенных между максимальным и минимальным значениями функции. На следующем графике отображаются только изолинии 30 уровней.

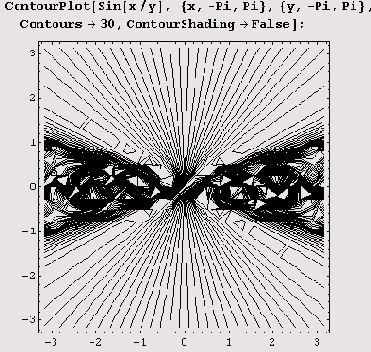
Если же нужно отображать только изолинии заданных уровней, то опцию Contours нужно установить равной списку этих уровней.

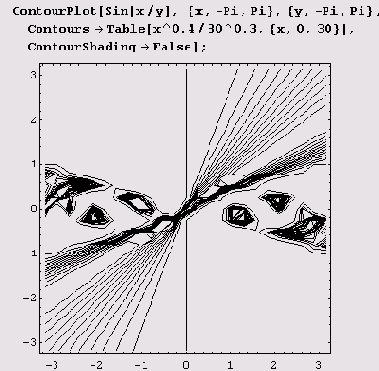
Список стилей контурных линий можно задать в опции ContourStyle. Например, если установить ContourStyle->{{RGBColor[1,0,0]},{RGBColor[0,0,l]}}, то будет чередоваться красный и синий цвета контурных линий.

По умолчанию значение опции PlotPoints равно 25. При увеличении этого значения на графике могут появиться дополнительные детали. Вот как изменится предыдущий график, если его установить равным 50.

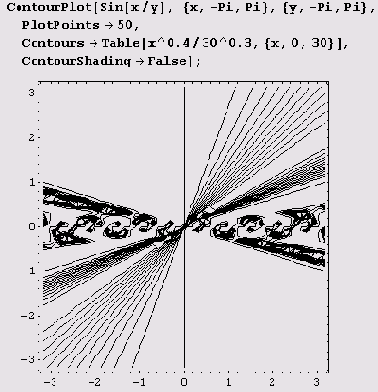
Кроме перечисленных, функция ContourPlot имеет также опции AxesOrigin, Compiled и ContourSmoothing.

При установке ContourSmoothing->True происходит сглаживание линий уровня.

Функция ListContourPlot

Эта функция вычерчивает фафики функций, заданных таблично. В приведенном ниже примере таблица значений функции сгенерирована с помощью функции Table.

Фактически в таблицу заносятся значения функции cos(sin(;c2 + ;y2)), к которым добавляется случайное возмущение с помощью функции Random [Real, {-0.2,0.2}].

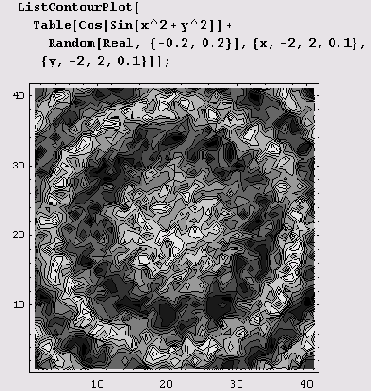
Графики плотности

Для построения графиков плотности в системе Mathematica имеются функции DensityPlot и ListDensityPlot.

Функция DensityPlot

Эта функция отображает значения исследуемой функции в ячейках регулярной сетки с помощью окрашивания этих ячеек либо в серый цвет, либо в цвета палитры, задаваемой функцией Hue. Ниже приведен пример такого графика с окраской в серые тона.

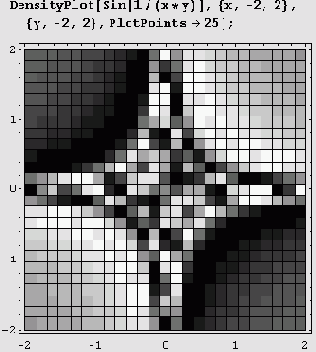
При увеличении значения опции PlotPoints количество деталей, естественно, возрастает.

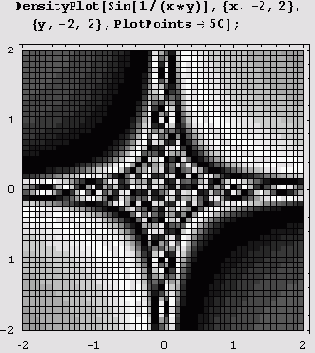
Если хотите убрать разграфку на ячейки (сетку), установите Mesh->False.

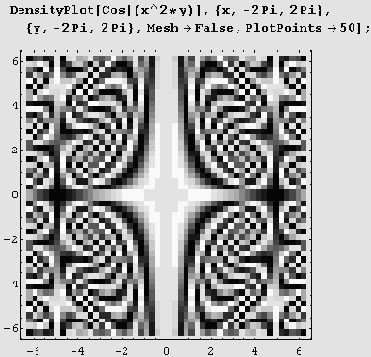
Стиль ячейки определяет опция MeshStyle. В этой опции можно использовать Dashing, Thickness, GrayLevel, Hue И RGBColor.

Дополнительно у функции DensityPlot есть опции ColorFunction и Compiled.

Функция ListDensityPlot

С помощью этой функции строится график плотности таблично заданной функции. В приведенном ниже примере сначала генерируется таблица, а затем применяется функция ListDensityPlot для построения графика плотности по табличным данным.

Конечно, по умолчанию отображается сетка.

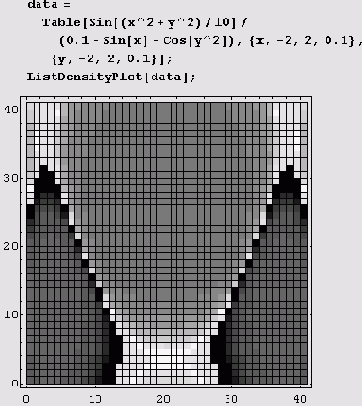
Специальные виды графиков

К специальным видам графиков относятся диаграммы, графики с текстовыми данными и огромное множество других видов.

Диаграммы и гистограммы

Этот вид графиков в системе Mathematica весьма многочисленный. Ни численностью, ни возможностями оформления этого вида графиков система Mathematica не уступает самым лучшим специализированным пакетам. Рассказывать обо всем этом богатстве с помощью черно-белых рисунков — значит отвергать пословицу: лучше один раз увидеть, чем сто раз услышать. Поэтому я не стану утомительно перечислять всевозможные опции и приводить серенькие рисунки. Если есть потребность, вызовите справочную систему И найдите описание функций BarChart, GeneralizedBarChart, StackedBarChart, PercentileBarChart, PieChart, Histogram и их многочисленных опций, призванных удовлетворить самые изысканные вкусы. Впрочем, мне кажется, что все диаграммы наиболее эффектно смотрятся лишь в цвете.

Графики с текстом

Что бы вы сказали о картине, на которой художник с помощью текста подписал бы все детали. Ну, например, чтобы вы сказали о Джоконде, если бы она пестрела надписями вроде "левая рука", "правая рука", "левый мизинец", "правый мизинец", "портьера", "штора", "левый глаз", "правый глаз", "улыбка" и т.д. Думаю, Джоконда потеряла бы свой шарм. Но бывают случаи, когда надписи просто необходимы. На географических картах, например. Вы знаете, как их сделать. Но, оказывается, есть специальные функции, которые для изображения точки используют не маленький кружочек, а цифры или даже любое выражение системы Mathematica! При этом вы можете отображать точку или только надпись.

Функции TextListPlot и LabeledListPlot

Функции TextListPlot и LabeledListPlot можно вызвать тремя способами.

1-й способ. TextListPlot [ у₁ , у₂, ...} и LabeledListPlot [ y₁ , у₂, ...]. При этом способе точка с координатами (/', у,) помечается с помощью числа /. Если используете TextListPlot, то даже точки не увидите — только число. Вот первые 25 десятичных знаков основания натуральных логарифмов.

data=First[RealDigits[N[E,25]]]

{2,7,1,8,2,8,1,8,2,8,4,5,9,0,4,5,2,3,5,3,6,0,2,8,7}

А вот как полученные данные можно отобразить на графике.

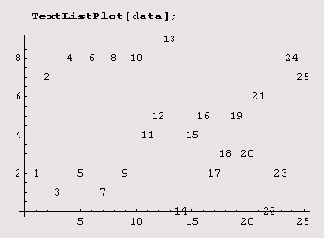
Точки графика просто изображаются их номерами. А вот функция LabeledListPlot отображает точки и перенумеровывает их.

2-й способ. TextListPlot [ {x₁, у₁}, { х₂, у₂}, ...] и LabeledListPlot [ { х₁, у₁ }, { х₂, у₂}, ...]. При этом способе точка с координатами (*,, yt) помечается с помощью числа .

3-й способ. TextListPlot [{ х₁, у₁, выражение^, {х₂, у₂, выражениег}, ...] и LabeledListPlot [{ х}, у₁ , выражение^ , { х₁, у₂, выражение?.}, ...]. При этом способе точка с координатами (х₁, y₁) помечается с помощью выражение,.

Пусть, например, имеем следующее.

А вам написать Спираль по спирали слабо?

Функция MultipleListPlot

Честно говоря, строку "Колебаться, колебаться, колебаться завещал нам Великий Синус... " записывать по синусоиде с помощью функции LabeledListPlot несколько хлопотно, так как нужно написать выражение, выбирающее нужный символ из списка. В пакете <<Graphics`MultipleListPlot` функция MultipleListPlot делает это автоматически. Вообще-то, эта функция предназначена для создания графиков нескольких табличных функций и потому вызывается так: MultipleListPlot [сиисок,, список^, ...]. Вот синус и косинус, заданные таблично, на одном графике.

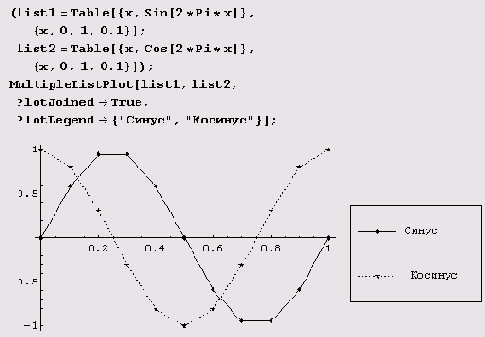
Количество опций этой функции просто поражает. Опция SymbolLabel позволяет указывать последовательность символов, которые используются для пометки точек графика.

Пусть имеем следующее.

list3=Table[{x*Sin[2 Pi x],-x*Cos[2 Pi x] }, {x,0,1,0.05 } ];

Тогда получим вот это.

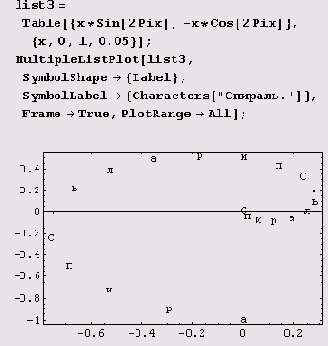
Построение графиков неявно заданных функций — функция ImplicitPlot пакета Graphics`ImplicitPlot`

Труднее всего, пожалуй, рисовать графики неявно заданных функций. Для вычерчивания графиков таких функций в системе Mathematica предусмотрен пакет Graphics`ImplicitPlot`, который загружается обычным образом: <<Graphics`ImplicitPlot`. В нем для построения графиков неявно заданных функций имеется функция ImplicitPlot. Ее первым параметром всегда является уравнение, определяющее неявно заданную функцию. Функция одной переменной задается неявно с помощью уравнения. Вид этого уравнения может быть любым допустимым в системе Mathematica; совсем не обязательно его приводить к виду F(x, у) = 0. Уравнение в системе Mathematica имеет вид левая часть == правая часть. Обратите внимание на двойной знак равенства, соединяющий левую и правую части. Уравнение нельзя записать с одним знаком равенства, т.е. в виде левая часть = правая часть, поскольку это присваивание. Функция ImplicitPlot пакета Graphics`ImplicitPlot` используется для построения графиков неявно заданных функций одной и двух переменных.

Построение графика неявно заданной функции одной переменной

При построении графика неявно заданной функции одной переменной применяются два метода:

решение уравнения; нужно задать интервал изменения переменной;
нахождение линии уровня; задаются интервалы изменения обеих переменных.

Построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале методом решения уравнения

При построении графика неявно заданной функции одной переменной различаются два случая:

построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале;
построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале, из которого исключено несколько точек.

Чтобы построить график решения уравнения, найденный функцией Solve на интервале изменения переменной (xmin, xmax), нужно вызвать функцию ImplicitPlot [уравнение, {переменная, xmin, xmax}].

Пример 9.14. "Кривая дьявола". Эта кривая задается уравнением dс⁴ -9cⁿ:2 = уⁿ -100y². С помощью функцииImplicitPlot рисуется она совсем просто.

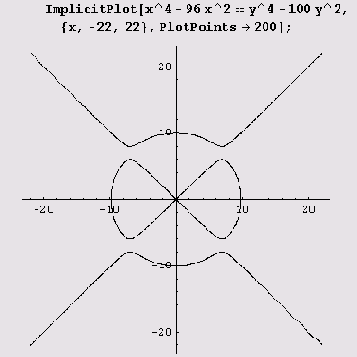
Пример 9.15. Кривая х⁴+ у⁴ = х² + у². Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что в полярных координатах она задается уравнением вида

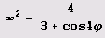
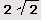
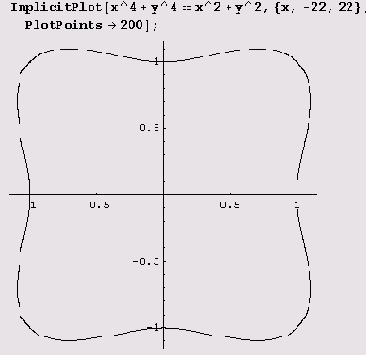
Заметьте, что хотя для х интервал изменения был взят с большим запасом, график увеличен за счет того, что функция ImplicitPlot сообразила, что отображать весь заданный интервал нет необходимости.

Пример 9.16. Кривая у⁵ + x⁴ = ху². Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что все интересные детали лежат в интервале (-10, 10).

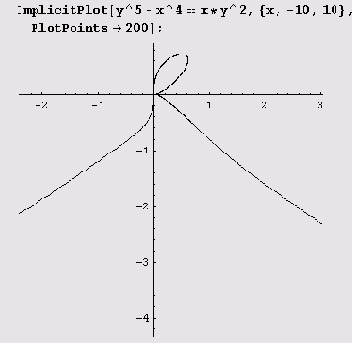
По поводу этого и других графиков неявно заданных функций нужно сделать следующее замечание. Система Mathematica вычерчивает графики очень аккуратно и весьма точно. Однако в случае неявно заданных функций свойства вычерчиваемых кривых далеко не всегда очевидны из уравнения. Аккуратное вычерчивание иногда также может скрывать эти свойства. Например, иногда очень трудно отличить криволинейную дугу от отрезка прямой, а из-за этого можно пропустить точку перегиба. В ГУ квадранте вычерченного системой Mathematica графика, например, есть точка перегиба. Однако на глаз заметить ее очень трудно, поскольку криволинейная дуга почти сливается с прямой. В учебных пособиях в таких случаях обычно жертвуют точностью и приводят эскиз графика, на котором характерные точки кривой легко заметны на глаз. Система Mathematica же точностью жертвовать не может, и потому иногда требуется дополнительное исследование графика, которое можно провести, конечно же, с помощью системы Mathematica.

В первом квадранте, например,

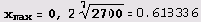
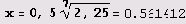
Пример 9.17. Кривая x⁵ + у⁵ = ху². Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что все интересные детали лежат в интервале (-1, 1).

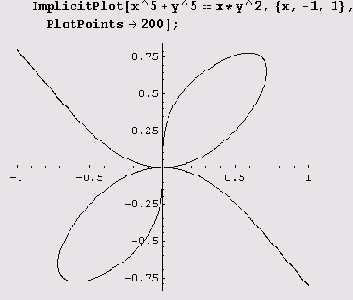
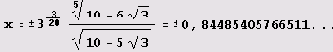
График опять вычерчен очень аккуратно и весьма точно. И опять очень трудно отличить криволинейную дугу от отрезка прямой, и из-за этого абсциссы 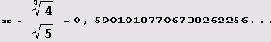точек локальных экстремумов в I и III квадрантах, а также уравнения вертикальных касательных 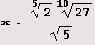² с первого взгляда.

Трудные случаи построения графика неявно заданной функции одной переменной в заданном интервале изменения переменной с помощью функции ImplicitPlot. Построение графика неявно заданной функции одной переменной даже в заданном интервале изменения переменной — весьма непростая задача. Функция ImplicitPlot во многих случаях справляется с ней блестяще. Но далеко не во всех случаях. Вот тривиальный пример.

ImplicitPlot[Min[x,у]==1,(х,-22,22},PlotPoints->200];

 Solve::dinv :

The expression Min'0'1* [x, y] involves unknowns in more than one argument,

 so inverse functions cannot be used. More...

ImplicitPlot::epfail: Equation Min[x,y]==l

could not be solved for points to plot.

Конечно, уравнение Min[x,y]= =1 определяет неявно заданную функцию, график которой представляет собой прямой угол с вершиной в точке (1; 1), причем стороны его параллельны осям координат. Потому с этим примером должен без труда справляться даже шестиклассник. Впрочем, функция ImplicitPlot с этим графиком тоже может справиться, но после некоторой подсказки.

Вот еще один трудный (для функции ImplicitPlot) случай.

С этим примером должен без труда справляться даже восьмиклассник. (Правда, если он хочет участвовать в районной (городской) олимпиаде или поступить на мехмат.) И вот еще один совсем "позорный" пример.

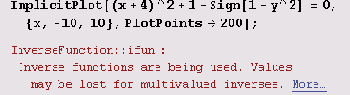
А вот этот простенький пример считается неоправданно долго.

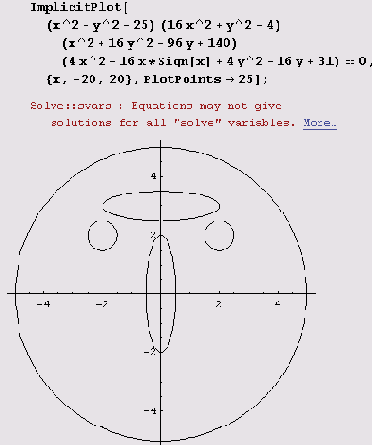
Это поистине удивительно, потому что графики для всех сомножителей строятся очень быстро!

Предостережение. Заглянув в справочную систему, вы можете попытаться построить этот график так

ImplicitPlot[x^2+y^2-25==0,16 х^2+у^2-4==0,

х^2+16у^2-96у+140==0,

4x^2-16x*Sign[х]+4у^2-16у+31==0,

{х,-20,20},

PlotPoints->25];

или так

ImplicitPlot[x^2+y^2-25==0,16

х^2+у^2-4==0,

х^2+16у^2-96у+140==0,

4х^2-16х*Sign[х]+4у^2-16у+31==0,

{х,-20,20},{у,-20,20),

 PlotPoints->25];

Вы увидите, что ничего не произойдет! На самом деле вызов нужно записать вот так

ImplicitPlot[{x^2+y^2-25==0,16

х^2+у^2-4= =0,

х^2+16у^2-96у+140==0,

4х^2-16х*Sign[х]+4у^2-16у+31==0},

{х,-20,20},

PlotPoints->25];

или так

ImplicitPlot[{x^2+y^2-25==0,16

 x^2+у^2-4==0,

х^2+16у^2-96у+140==0,

4хл2-16х*Sign[х]+4у^2-16у+31==0},

{х,-20,20},{у,-20,20),

PlotPoints->25];

Фактически это построение графиков нескольких неявных функций. Мы этот случай рассмотрим чуть позднее.

Построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале, из которого исключено несколько точек.

Чтобы построить график решения уравнения, найденного функцией Solve на интервале изменения переменной (xmin, xmax) , из которого исключено несколько точек, нужно в вызове функции ImplicitPlot [уравнение, (переменная, xmin, xmax}] между xmin, и хmах через запятую перечислить все исключаемые точки. Впрочем, функция ImplicitPlot, как правило, сама избегает значений, которые доставляют хлопоты, и потому прибегать к этой форме вызова не приходится даже в следующих двух классических случаях.

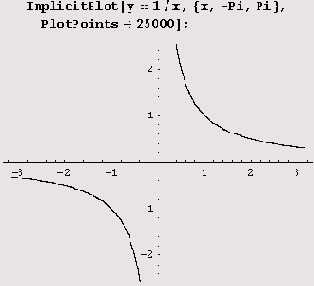
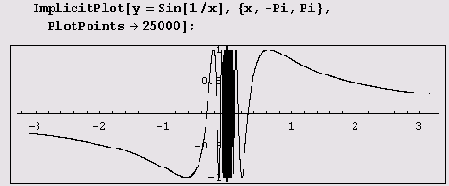
Построение графика неявно заданной функции одной переменной при изменении переменных на заданных интервалах методом нахождения линии уровня

Уравнение F, (х, у) = F2 (х, у) можно записать в виде F, (х, у) - F, (х, у) = 0. Так что фактически вместо решения уравнения F, (х, у) = F2 (х, у) можно найти линию уровня функции F, (х, у) - F2 (х, у), на которой она равна 0. Как дать такую подсказку функции ImplicitPlot? Очень просто: нужно указать интервалы изменения обеих переменных. Рассмотрим примеры, когда это полезно.

Ранее с помощью вызова ImplicitPlot[Min[x,у] ==1, {x,-22,22},PlotPoints-> 200]; мы не смогли построить график неявной функции Min[x,y]==l. А вот с подсказкой ImplicitPlot[Min[x,y]==l,{х,-22,22},(у,-22,22},PlotPoints->200]; график строится мгновенно. Вызов

ImplicitPlot[ (х^2+у^2-25) (16 х^2+у^2-4)*

*(х^2+16у^2-96у+140)

 (4х^2-16х*Sign[х]+4у^2-16у+31)==0,

{х,-5,5}, (у,-5,5),

PlotPoints->25];

строит график более десяти минут, а вызов

 ImplicitPlot [(х^2+у-2-25) (16 х^2+у^2-4)

 (х^2+16у^2-96у+140)

 (4x^2-16x*Sign[х]+4у^2 -1бу+31)==0,

{х,-5,5}, {у,-5,5),

 plotPoints->250];

нужно менее трети секунды.

Вот еще один график, который без подсказки не строится вообще.

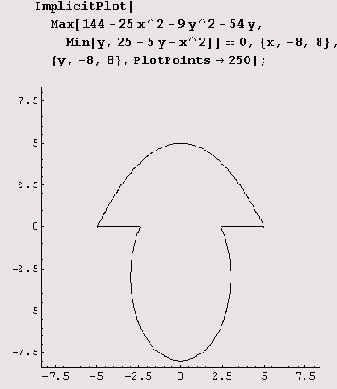
График

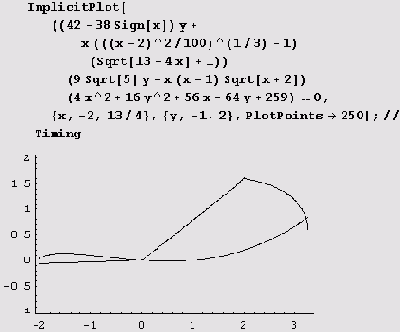
строится за 0,344 секунды. Важна ли тут подсказка (у,-1,2}? Оказывается, график можно построить и без нее, но это займет немалое время даже при PlotPoints->25.

Построение графиков нескольких неявных функций

Построение таких графиков теоретически сводится к построению графика одной неявной функции. Пусть нужно построить графики неявных функций, заданных уравнениями

F₁(х, у) = Ф₁(х, у), F₂ (х, у) = Ф₂(х, у), F₃ (х, у) = Ф₃(х, у), ..., F_n(x, у) = Ф_n(х, у).

Тогда мы можем привести эти уравнения к виду F₁(х, у) - Ф₁(х, у) = 0, F₂ (х, у) - Ф₂(х, у) = 0, F₃ (х, у) - Ф₃(х, у) = 0, ..., F_n (х, у) - Ф_n(х, у) = 0 и построить график (F₁(х, у) - Ф₁(х, у))( F₂(х, у) - Ф₂(х, у))( F₃ (х, у) - Ф₃(х, у))...( F_n (х, у) - Ф_n(х, у)) = 0.

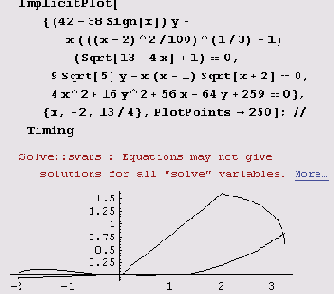
Но на практике лучше поступать не так, а совсем наоборот. Например, построение графика

ImplicitPlotf

((42-38Sign[x])y+x^(х-2) ^2/100) ^ (1/3) -1)

 (Sqrt [13-4х]+1) )

 (9Sqrt[5]-x(x-l)Sqrt[x+2])(4х^2+16у^2+56х-64у+259)==0,

{х,-2,13/4),

PlotPoints->25];//Timing

можно заменить построением следующего графика.

График

ImplicitPlot[((4у+х^2)^2+Sign[х^2+2х]+1)

((х^2+у^2)^(5/2)-4х(х^2-у^2))==0, {х,-5,5},

PlotPoints->25];//Timing

можно строить часами, а график

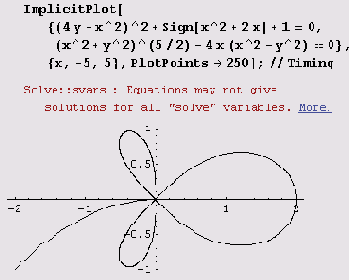
строится всего за 21,641 секунды. Этот график можно попытаться построить и как линию уровня.

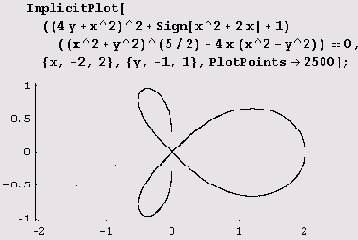
Этот способ потребует всего лишь 17,859 секунды. Но обратите внимание на отсутствие ножки у трилистника. Вместо нее на экране всего лишь несколько почти незаметных точек. Попытка же увеличения значений параметров PlotPoints и PlotDivision может привести к неоправданно большому запросу виртуальной памяти и к пробуксовыванию. Мораль: при построении контурных линий некоторые ветви могут пропадать.

Вот что происходит при построении некоторых графиков.

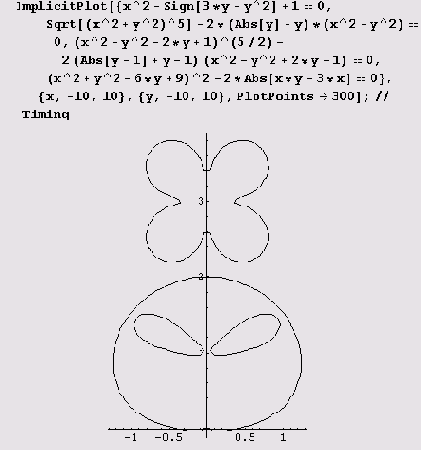
График

ImplicitPlot[
Sqrt[(х^2+у^2)^5]- 2*(Abs[у]+у)*(х^2+у^2)==0,

(х,-10,10},{у,-10,10},

PlotPoints->300];//Timing

вообще выглядит пустым. График же

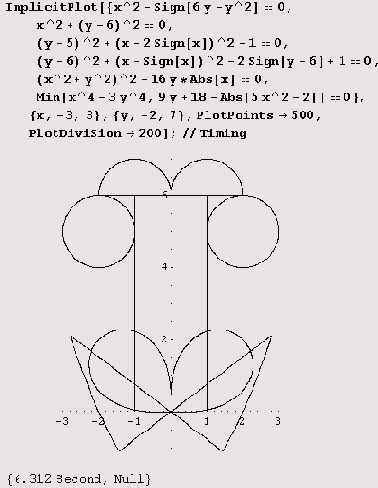
рисуется, но не без проблем: некоторые параметры (PlotPoints->500, PlotDivision->200) пришлось подбирать, иначе мелкие штрихи пропадают. Еще большие проблемы возникают при вычерчивании следующего графика.

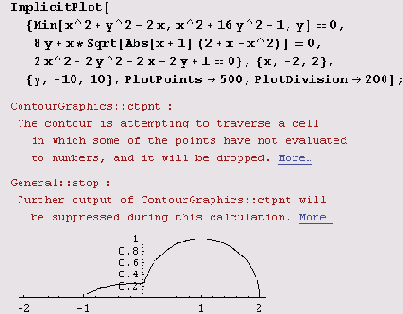
График же

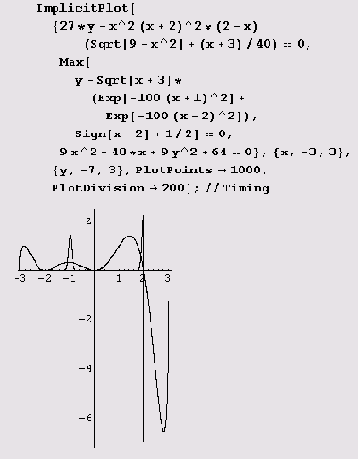
вычерчивается без проблем.

Так же легко вычерчивается и следующий график.

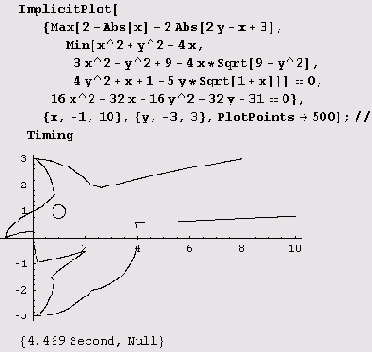
График же

построению почти не поддается: при изменении параметров PlotPoints->l000, PlotDivision->2500 в нем часто исчезают те или иные детали. Не удается его построить ни вот так

ImplicitPlott((х+4)^2+1-Sigm[1-у^2])

((х+3)^2+у^2+2Sign[х+3]+1)




((2х+3)^2+у^2-1)((х^2-х)^2-Sign[1-у^2]+1)

(у^2+Sign[х^2-х]+1) ((х-3)^2+у^2+2Sign[х-3]+1)

((х-2)^2+(у-1)^2+Sign[2-х]+Sign[y-1]+1)

 ((х^2-9х+20)^2-Sign[1-у^2]+1)

((y+Abs[x-4]+Abs[x-5])^2-Sign[(х-4)(21/4-х)]+1)==0,

(х,-4,5},

PlotPoints->1000,PlotDivision->250];

ни вот так

ImplicitPlott{(х+4)^2+1-Sign[1-у^2]==0,

 (х+3)^2+y^2+2Sign[х+3]+1==0,

 (2х+3)^2+у^2-1==0, (х^2-х)^2-Sign[1-у^2]+1==0,

y^2+Sign[x^2-x]+l==0, (х-3)^2+y^2+2Sign[x-3]+l==0,

(x-2)^2+(y-l)^2+Sign[2-x]+Sign[y-l]+l==0,

(х^2-9х+20)^2-Sign[l-y^2]+l==0,

(y+Abs[x-4]+Abs[x-5])^2-Sign[(x-4)(21/4-х)]+1==0},

{х,-4,5},PlotPoints->1000,

PlotDivision->250];

В лучшем случае получаем кучу предупреждений и вот что.

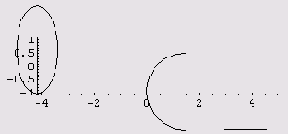
Мораль: графики многих неявных функций легко строятся с помощью функции ImplicitPlot, однако существуют невинно выглядящие мехматовские "приколы", при построении которых либо теряются дуги, отдельные точки, отрезки, либо же графики не строятся совсем. Иногда проблем удается избежать, если изменить метод построения графика (от решения уравнения перейти к построению линии уровня или наоборот). Однако это помогает далеко не всегда. Тогда приходится брать мехматовские учебники. Они не покажутся такими недоступными, если вы будете читать их, а система Mathematica будет делать то, что там написано! Очень часто всего лишь нескольких подстановок (их может выполнить система Mathematica) достаточно, чтобы перейти к параметрическому заданию графика.

Содержание раздела