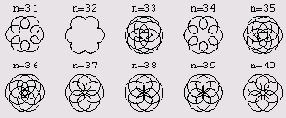Алгебра и пакет Mathematica 5
Несколько графиков на одном чертеже — функция GraphicsArray
Как вы уже знаете, функция GraphicsArray позволяет на одном листе (чертеже) нарисовать несколько графиков, расположив их в одну строку или в виде двухмерного массива. Однако если вы все графики вычерчиваете с помощью одной функции, например ParametricPlot, удобно предварительно установить те значения ее опций, которые совпадают у большинства графиков. Пусть, например, мы хотим установить опции
AspectRatio->Automatic и Axes->False. Вот как это делается.
SetOptions[ParametricPlot,AspectRatio->Automatic,Axes->False] ;
Теперь можем определить нужные нам графики и при необходимости задать значения тех опций, которые отличаются от установленных ранее. Пусть, например, на первом и третьем графиках вычерчиваются оси координат. Тогда для этих графиков устанавливаем
Axes->True.
Block[{$DisplayFunction=Identity},
pl=ParametricPlot[{Cos[t],Sinft]},{t,0,2Pi},Axes->True];
p2=ParametricPlot[{2Cos[t],Sin[t]),{t,0,2Pi}];
p3=ParametricPlot[{ (2Cos [t] -1) Cos [t-] , (2Cos [t]-1) Sin [t] },
{t,0,2Pi},Axes->True];
p4=ParametricPlot[{t Cos[t],t Sin[t]},{t,0,12Pi}];
p5=ParametricPlot[{t Cos[t]Sin[t],t Sin[t]Л2},{t,0,8Pi}];
p6=ParametricPlot[{Sin[2t]+Sin[5t],Cos[2t]+Cos[5 t]},{t,0,2Pi}];
p7=ParametricPlot[{Sin[2t]Sin[5t],Cos[2t]Sin[5t]},{t,0,2Pi}];
p8=ParametricPlot[{Cos[t]+l/2Cos[7t]+l/3 Cos[-17t+Pi/2],
Sin[t]+l/2 Sin[7 t]+l/3Sin[-17t+Pi/2]},{t,0,2Pi}];]
После этого формируем массив фафиков и отображаем его.
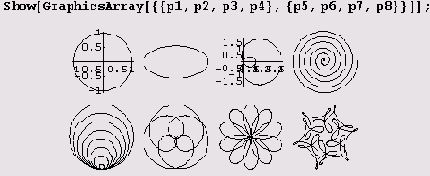
Функция GraphicsArray может быть полезна при подборе параметров.
Пример 9.18. Подбор параметров с помощью функции GraphicsArray. Предположим, вам нужно среди двухпараметрического множества кривых (напоминающих цветы) вида (R cos(az), R sin(fe)), где R = sin 5r, выбрать ту, которая ближе всего к окружности при условии, что параметры а и b принимают целые значения, причем 1<а<9 и 1<6<6. Можно, конечно, пересмотреть все 54 кривые по одной. Но если вы не уверены, что среди них есть окружность, лучше расположить все графики на одном чертеже. Однако в отличие от предыдущих примеров, где количество графиков было небольшим, в данном случае формирование массива лучше всего поручить системе Mathematica. Для этого как нельзя лучше приспособлена функция Table. Именно с ее помощью удобнее всего сначала сформировать двухмерный массив шириной 6 и высотой 9 графиков. Затем эти графики лучше всего отобразить на одном чертеже и выбрать (на глаз) те, которые, как вам кажется, наиболее подходят для вашей цели. Отобранные графики затем можно будет рассмотреть в деталях и выбрать наиболее подходящий из них. Вот как это делается в нашем случае.
Block[{k=5},Block[{a,b,r=Sin[k*z]},
Block[{XY={r*Cos[a*z],r*Sin[b*z]}),
Show[GraphicsArray[ Table[Table[ParametricPlot[XY,{z,0,2 Pi}],
{b,6}],{a,9}]]]]]]
Когда будете выполнять эту программу, перед вами промелькнет 54 графика, которые рассмотреть вы, конечно, не успеете. Зато в конце вы увидите следующую картинку.
Я думаю, вы без труда найдете здесь окружность.
Конечно, в рассмотренном примере нам немного повезло. Ведь параметры были последовательными натуральными числами. Благодаря этому было так легко организовать перебор их значений с помощью параметра функции Table. Но что делать, если нужно вычертить, скажем, четыре десятка кривых, параметры которых просто заданы таблицей?
Пример 9.19. Циклоиды. Пусть семейство циклоид задается параметрическим уравнением
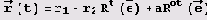ф —
поворот вокруг начала координат на угол φ. Пусть параметры г,, г2 и а заданы таблицей (всего 40 наборов параметров в таблице).
| № n/n |
r1 |
r2 |
а |
| 1 |
2 |
-1 |
1 |
| 2 |
3 |
- 1 |
1 |
| 3 |
3 |
-2 |
2 |
| 4 |
4 |
-1 |
1 |
Как начертить все нужные нам кривые, не задавая в их уравнениях параметры вручную? Для этого придется превратить таблицу в список наборов параметров.
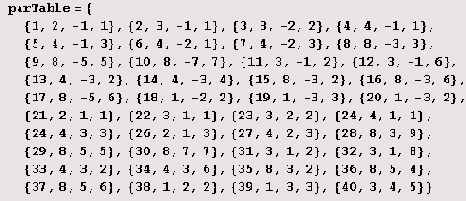
Заметьте, что порядковый номер включен в набор параметров первым элементом. Это значительно облегчает поиск нужного набора параметров в таблице. Теперь мы хотим написать программу, которая печатает на одном чертеже графики с порядковыми номерами в заданном диапазоне, располагая их по т штук в ряду.
Сначала определим вращающийся единичный вектор.
Rphi[phi_]:={Cos[phi],Sin[phi]}
После этого можно дать определение функции PolarXYAB для наших циклоид.
PolarXYAB[t_,г 1_,r2_,a_,omega_]= r1+r2*Rphi[t]+a*Rphi[omega*t]
Теперь определим функцию, рисующую отдельный график.
gg[n_]:=Block[{plot,rl=parTable[[n]] [[2]],r2=parTable[[n]] [ [3]],
a=parTable[[n]] [[4]]},
plot=ParametricPlot[PolarXYAB[t,rl,r2,a,omega],
{t,0,2 Denominator[omega]Pi}, Axes->False,
PlotLabel->"n="oToString [n] ] ]
Теперь можем нарисовать, например, первые 15 циклоид, параметры которых соответствуют порядковым номерам с 1 по 15 в нашей таблице. (Они все будут круговыми циклоидами.) Вот как это делается.
Block[{n,m=5,omega=l/7},
Show[GraphicsArray[
Table[Table[gg[n=(a-l)*m+b],{b,m}],{a,3}]]]]
Перед вами промелькнут 15 графиков, а в конце вы увидите вот что.
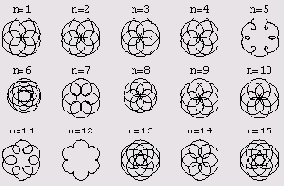
Чтобы начертить графики 16 и 17, в программе изменяется лишь m и начальный порядковый номер.
Block[{n,m=2,omega=l/7},
Show[GraphicsArray[
Table[Table[gg[n=15+(a-1)*m+b],{b,m}],{a,!)]]]]
В конце вы увидите следующее.
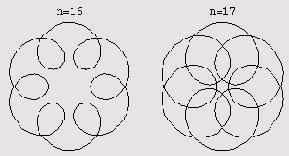
Это развернутые циклоиды. Нарисуем, наконец, развернутые циклоиды, которые образуются, когда подвижная окружность содержит внутри себя неподвижную. (Это графики с 18 по 20.)
Block!{n,m=3,omega=l/7},
Show[GraphicsArray[
Table[Table[gg[n=17+(a-1)*m+b],{b,m}],{a,1}]]]]
В результате вы увидите вот что.
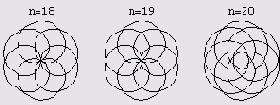
Теперь нарисуем 2 ряда развернутых циклоид. (Это графики с 20 по 30.)
Block[(n,m=5,omega=l/7),
Show[GraphicsArray[
Table[Table[gg[n=20+(a-1)*m+b],{b,m}],{a,2}]]]]
Вы увидите следующее.
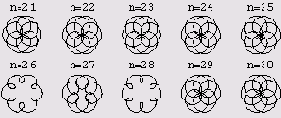
Вспоминаем, наконец, об оставшихся 10 графиках. В программе достаточно изменить лишь начальный порядковый номер.
Block[{n,m=5,omega=l/7},
Show[GraphicsArray[
Table[Table[gg[n=30+(a-1)*m+b],{b, m}], {a, 2}]] ] ]
А вот и сами графики.
|