Алгебра и пакет Mathematica 5
Вычерчивание графиков
Для вычерчивания графиков образов в трехмерном пространстве чаще всего используются следующие функции трехмерной графики:
Plot3D, ParametricPlot3D и ListPlot3D.
Построение графика функции двух переменных
Простейшими способами задания функции двух переменных являются явный (т.е. в виде равенства z=fix, у)) и табличный. Для изображения графика функции двух переменных, заданной в виде равенства z=fix, у), предназначена функция
Plot3D, a графики таблично заданных функций двух переменных можно начертить с помощью функции
ListPlot3D.
Построение поверхности, заданной уравнением z = f(x, у), — функция Plot3D
Вызов Plot3D[/, [х, xmin, xmax}, (у, ymin, ymax}} генерирует график/как функции х и у. То же самое делает и вызов
Plot3D[{/, оттенок], (х, xmin, xmax), {у, ymin, ymax} ], но при этом указывается оттенок графика. Функция оттенок должна возвратить одну из директив
GrayLevel, Hue или RGBColor либо объект SurfaceColor. На приведенном ниже рисунке с помощью функции оттенок на пересеченной местности, описываемой уравнением
z = sin(x+3 sin у), нанесены "солнечные пятна" и "тени" (по всей видимрсти, от туч).

Построение графика таблично заданной функции двух переменных — функция ListPlot3D
Функция ListPlot3D служит для построения графика таблично заданной функции двух переменных. Вызов функции имеет вид
ListPlot3D [таблица] или ListPlot3D [таблица, таблица оттенков]. Таблица должна быть прямоугольным массивом вещественных чисел. Иными словами, она должна быть списком списков одинаковой длины. Числа в ней интерпретируются как значения функции. Если таблица имеет размер /пхл, то таблица оттенков должна иметь размер
(m- 1)х(n- 1). Элемент таблицы оттенков и в самом деле должен быть оттенком — он должен либо быть объектом SurfaceColor, либо иметь тип
GrayLevel, Hue или RGBColor. Ниже показан
горный ландшафт, сгенерированный с помощью таблицы функции г = е~5а*'у, к которой добавлены случайные возмущения.
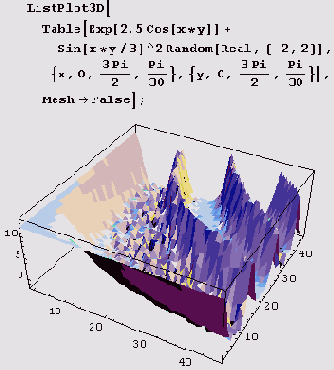
Построение параметрически заданных кривых и поверхностей — функция ParametricPlot3D
Далеко не все поверхности можно задать уравнением z = f(x,y)) или таблично. Часто гораздо удобнее задавать их параметрически. Параметрически можно задать также кривые в пространстве. Параметрически заданные в трехмерном пространстве двухмерные поверхности или одномерные кривые можно рисовать с помощью функции
ParametricPlot3D. Проекцией нарисованной ниже кривой является фигура Лиссажу.
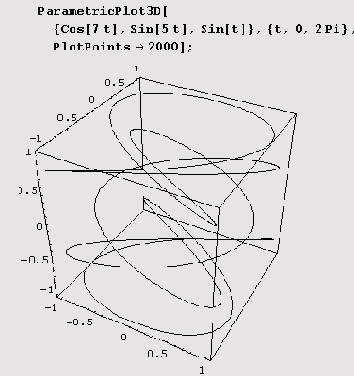
Вызов ParametricPlot3D[ {xt, yt, it], {t, tmin, tmax}] возвращает пространственную кривую, параметризованную переменной /, изменяющейся от tmin до
tmах.
Вызов же ParametricPlot3D[ {xt, yt, zt}, {t, tmin, tmax}, {u, umin, umax}]
возвращает поверхность в пространстве, параметризованную переменными t и и, изменяющимися от tmin до tmax и от umin до итах соответственно. Можно указать оттенок рисуемого образа, для этого вызов нужно записать так:
ParametricPlotSD [{xt, yt, zt, оттенок}, ...]. Ну и, конечно, можно нарисовать несколько образов. Для этого вызов записывается так:
ParametricPlotSD [{(xlt, ylt, zJt}, (x2t, y2t, z2t), ...}, ...]. На рисунке ниже хорошо видно, что кривые x=tcost, y=tsint, z= 2t и х= 2 t cos
t, у = 2t sin t, z = 2 t лежат на конусах.
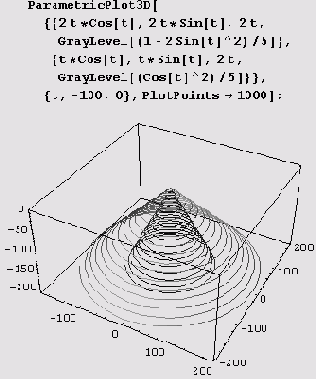
Для оттенения этих конических винтовых линий (создания эффекта их освещения) применялась функция
GrayLevel. Это "освещение" несколько необычно: там, где одна коническая винтовая линия темнеет, вторая светлеет.
На следующем рисунке показаны конусы с общей вершиной.
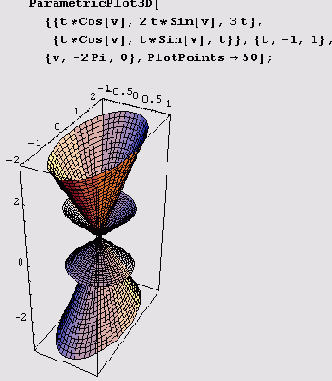
Поверхности вращения — пакет Graphics`SurfaceOfRevolution`
Для рисования поверхностей вращения удобнее применять пакет Graphics`SurfaceOf Revolution`, который загружается как обычно:
<<Graphics`Surf асеOf Revolution`. Вызов SurfaceOfRevolution [t, {x, xmin, xmax}]
строит поверхность, которая получается в результате вращения кривой z = f(x) вокруг оси аппликат. Вот пример.
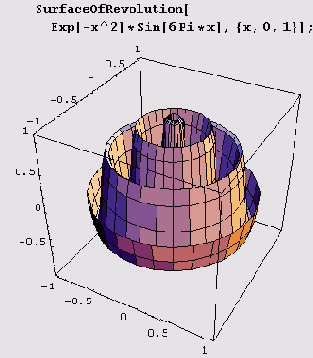
Вращать можно и плоскую параметрически заданную кривую х = fx(t), у = fy(t), но тогда вызов нужно записать вот так:
SurfaceOfRevolution[ (fx, fy], {t, a, b}].
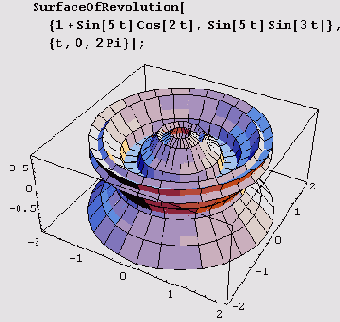
Более того, вращать можно и пространственную параметрически заданную кривую x=fx(t), у = fy(f), z=fz(t), но тогда вызов нужно записать вот так:
SurfaceOf Revolution[ [fx, fy, ft}, {t, a, b)].

Иногда нужно нарисовать не всю поверхность вращения, а только ее часть, соответствующую углам вращения в, таким, что
θ min< θ <
θmax . Тогда в вызов нужно добавить диапазон углов (theta, thetamin, thetamax}. Например, в случае поверхности, образованной вращением кривой, заданной уравнением
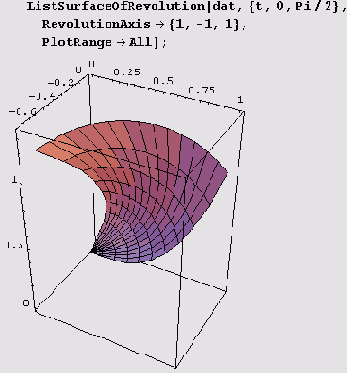
у =f(x), вызов нужно записать так: SurfaceOfRevolution[t, {х, xmin, xmax}, {theta, thetamin, thetamax}}. Конечно, аналогичное добавление нужно сделать и для случаев параметрического задания вращаемой кривой. Ниже представлено изображение абстрактной скульптуры, полученное таким способом из параметрически заданной пространственной кривой.
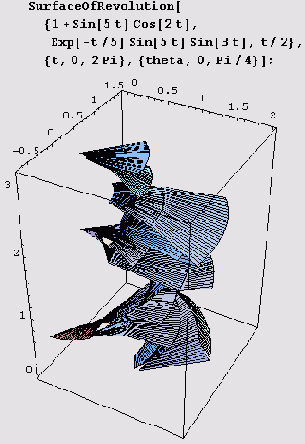
Наконец, иногда нужно указать ось вращения, проходящую через начало координат. Для этого можно воспользоваться опцией RevolutionAxis. Если ось вращения лежит в плоскости xOz, то в опции RevolutionAxis достаточно указать координаты х и г точки, отличной от начала координат: RevolutionAxis->{x,
r). В иных случаях придется указать все три координаты любой, отличной от начала координат точки, инцидентной оси вращения: RevolutionAxis->{x, у,
r)
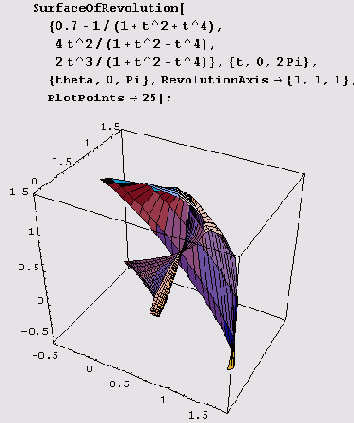
Вращать, конечно, можно и таблично заданные кривые. Для этого предназначена функция
ListSurfaceOfRevolution. Вот возможные обращения к ней:
ListSurfaceOf Revolution [{точка1, точка2,...}},
ListSurfaceOfRevolution [{точка1,точка2, ...},
(theta, thetamin,thetamax}}.