Алгебра и пакет Mathematica 5
Многочлены
Чтобы проверить, что выражение ехрr есть многочлен по некоторой переменной
var, нужно вызвать функцию PolynomialQ [елрг, var]. Результат будет
True, если ехрr является многочленом по переменной var, и
False — в противном случае.
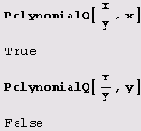
В случае нескольких переменных при проверке необходимо указать список переменных:
PolynomialQ [expr, [varl, var2,...}].
PolynomialQ[ху,{х,у}]
True
Выражение PolynomialQ [ехрr] равно True, если ехрr является полиномом относительно каких-либо переменных. В противном случае результат равен
False.
PolynomialQ[ху,{х,у}] True
PolynomialQ[(Pi+x)у] True
PolynomialQ[1/z+xy] False
Чтобы узнать общее число слагаемых в многочлене poly, можно вычислить выражение Length [poly]. Но не забудьте перед этим раскрыть скобки.
PolynomialQ[(a+b+c+d)^100]
True
Lengthf(a+b+c+d)^100] 2
Length[Expand!(a+b+c+d)^100]]
176851
Функция Variables, примененная к. poly, дает список всех независимых переменных в полиноме poly.
Variables[(a+b+c+d)^100]
{a,b,c,d}
Коэффициенты
Выражение Coefficient [poly, form] имеет своим значением коэффициент при выражении form в полиноме poly.
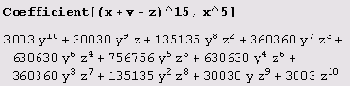
Выражение Coefficient [poly, form^n] эквивалентно Coefficient [poly, form, n].
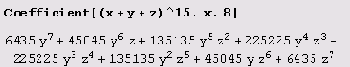
Результат вычисления выражения CoefficientList [poly, form] представляет собой список коэффициентов при степенях form в полиноме poly. Список составляется в порядке возрастания степеней.
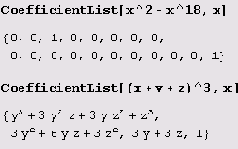
Список коэффициентов можно привести по определенному модулю.
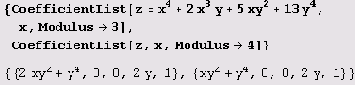
Приведение к каноническому виду
Приведение многочленов к каноническому виду выполняется путем раскрытия скобок и приведения подобных.
Разложение на множители
Разложение многочленов на множители над полем рациональных чисел выполняет функция Factor.
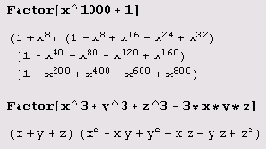
Разложение на множители выполняет не только функция Factor, но и функции FactorList и FactorTerms. В результате вычисления выражения FactorList [poly] получается список множителей полинома poly вместе с показателями степеней, с которыми множители входят в разложение poly на множители. Первый элемент списка есть общий численный множитель — так называемое содержание многочлена. Если содержание многочлена равно единице, то список начинается с {1,1}.
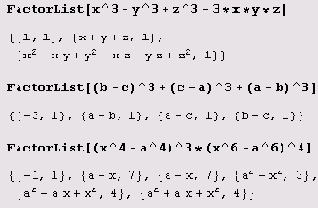
Функция FactorTerms позволяет вынести общий числовой множитель.
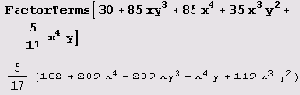
Вызов FactorTerms [poly, x] позволяет вынести общий множитель, не зависящий от х; FactorTerms [poly, {xl, x2, ...}] последовательно выделяет множители, не зависящие от x1, х2 и т.д. Вычисление выражения FactorTermsList [poly, (xl, x2, . . .}] дает список множителей poly. Первый элемент в списке есть общий числовой множитель, второй — множитель, не зависящий ни от одного из x1, х2, ... . Последующие элементы есть множители, не зависящие от как можно большего числа переменных x1, х2, ....
Деление многочленов
PolynomialQuotient [polyl, poly2] дает частное от деления многочлена poly1 на многочлен poly2, a PolynomialRemainder [poly1, poly2] — остаток.
Наибольший общий делитель многочленов
Важнейшими операциями при работе с полиномами являются нахождение наибольшего общего делителя и наименьшего общего кратного. Выражение PolynomialGCD [poly], poly2] представляет собой наибольший общий делитель многочленов polyl и poly2. При вычислении наибольшего общего делителя все символьные параметры в полиномах трактуются как переменные, и деление на них не допускается.
PolynomialGCD[х^3000-1, х^1503-1]
-1 + х3
Наименьшее общее кратное многочленов
Выражение PolynomialLCM[poly2, poly2] представляет собой наименьшее общее кратное многочленов poly1 и poly2.
Результант
Выражение Resultant [polyl, poly2, var] представляет собой результант многочленов poly1 и poly2, рассматриваемых как многочленов от переменной var.
Resultant[а*х^2+b*х+с, 2а*х+b, х] -
ab2 + 4 а2 с