Алгебра и пакет Mathematica 5
Линейная алгебра
Произведения векторов и матриц
Скалярное произведение векторов и матриц обозначается точкой.
{a1, а2, a3}.{b1, b2, b3}
a1 b1 + a2 b2 + аз bз
Для вычисления векторного произведения векторов применяется функция Cross. Она обозначается крестиком. Вот как вычисляется обобщенное векторное произведение пяти векторов в шестимерном пространстве.
{1,3,4,5,7,6}х{2,4,5,7,8,1}х{4,5,3,1,2,7}х {3,3,3,4,2,5}х{4,2,1,2,2,5} {522,-1076,1379,-580,60,-55}
Нормы векторов и матриц
С помощью функции Norm можно вычислять разнообразные нормы векторов и матриц.
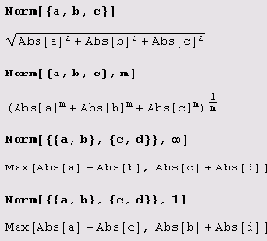
Обратные и псевдообратные матрицы
Совсем просто выполняется обращение неособенных матриц.
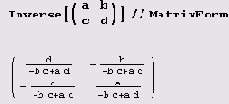
Особенная матрица не имеет обратной, но для нее можно определить псевдообратную, т.е. такую, произведение которой на исходную наименее уклоняется (по сумме квадратов) от единичной матрицы. (Конечно, для неособенной матрицы ее псевдообратная совпадает с обратной.)

С помощью псевдообратных матриц можно находить решения несовместных систем линейных уравнений.
Решение систем линейных уравнений
Пусть имеем систему линейных уравнений т х = v, где т — матрица системы, а v — вектор правых частей. Ее решение можно найти так.
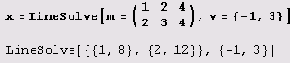
Вот как проверяется результат.
m.x-v
{0,0}
Имеются, конечно, и функции для специализированных методов, таких как Гауссово исключение, разнообразные декомпозиции, вычисление миноров и т.д.