Алгебра и пакет Mathematica 5
Интегрирование
Неопределенные интегралы, или первообразные
Чтобы найти неопределенный интеграл, можно воспользоваться командой Integrate:
Но не всегда все проходит так гладко. Например, в интеграле
не учтен случаи n= - 1. Вот еще пример.
Это тавтология. Между тем данный интеграл равен еx-1 при х<0 и 1-еx в остальных случаях. (Я здесь не опустил 1 для того, чтобы интеграл был непрерывен при х = 0.) Впрочем, многие интегралы, даже технически сложные для студентов, берутся без проблем:
Неберущиеся интегралы остаются без изменений или выражаются через специальные функции
Integrate[Ехр[х^2], х]
1/2π Erfi [x]
Определенные интегралы
Команда Integrate вычисляет и определенные интегралы, если в ней задать не только переменную интегрирования, но и ее пределы.
Чтобы приближенно вычислить определенный интеграл (например, неберущийся), можно воспользоваться командой NIntegrate.
Integrate[Exp[x]/x,{x,1,2}] -Gamma[0,-2]+Gamma[0,-1]
Nlntegrate[Exp[x]/x,{x,l,2}] 3.05912
Пример 10.1. Вычислим моменты инерции относительно осей координат 0х и 0у пластины с плотностью 1, ограниченной кривыми ху = 1, ху = 2, у = 2х, х = 2у и расположенной в I квадранте.
Нарисуем пластину.
Теперь нужно вычислить
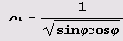(значение р на гиперболе ху = 1) и
и вычислили бы этот интеграл обычным путем. Но с помощью системы Mathematica все можно сделать проще:
Момент инерции относительно оси 0у можно вычислить точно таким же методом. Впрочем, очевидно, что момент инерции относительно оси 0у равен моменту инерции относительно оси Ох.
