Алгебра и пакет Mathematica 5
Векторный анализ
Операции векторного анализа легко определить самостоятельно. Для этого полезны функции
Outer и Inner. Функция Outer позволяет создать декартово произведение двух списков. Вот как можно, например, создать список пар, первый элемент которых берется из первого списка, а второй — из второго.
Outer[List,{a,b,c}, {d, e, f} ]
{{{a,d}, {a,e},{a,fn,{{b,d},{b,e},
{b,f}},{{c,cl},{c,e},{c,f}}}
Вот пример, связанный с конкатенацией строк.

Вот числовой пример.

Функция Inner немного похожа на скалярное произведение. Собственно говоря, inner[f, список1, список2, g] и есть скалярное произведение, в котором умножение замещается функцией/, а сложение — функцией g.
vl = {a1, a2, a3}; v2 = {b1, b2, b3>;
Dot[vl,v2] a1 b1 + 32 b2 + a3 bз Inner[Times,vl,v2,Plus]
a1 b1 + 32 b2 + a3 bз
Теперь можем определить основные операции векторного анализа.
Вот определение градиента. gradient[f ,x_List]:=Map[D[f,#]&,x] Вычислим градиент.
gradient[f[x,у, z], {x,y,z}]
{f(0,1,0)[x, y, z], f(0,1,0)[x, y, z],
f(0,1,0)D[x, y, z]}
Теперь определим гессиан hessian[f_,x_List]:=0uter[D,gradient[f,x],x] и вычислим его:
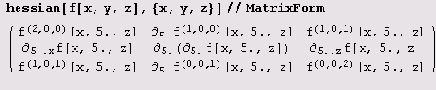
Определяем теперь лапласиан
laplacian[f_,x_List]:=Inner[D,gradient[f,x] ,x] и вычисляем его:
laplacian[f[x,y,z], {x,y,z}]
f(0,0,2)[x, y, z] + f(0,2,0)[x, y, z] f(2,0,0)[x, y, z]
Совсем несложно определить и якобиан.
jacobian[f_List,x_List]:=0uter[D,f,x] Вот пример его вычисления.
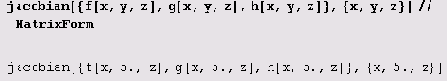
Наконец, определяем дивергенцию. divergence[f_List,x_List]:=Inner[D,f ,x] Вот пример ее вычисления.
divergence [ {f [x, у, z], g [x, у, z], h [x, y, z] }, {x, y, z} ]
h(0,1,0)[x, y, z] +
g(0,0,1)[x, y, z]+f(1,0,0)[x, y, z]
Вот еще несколько примеров выполнения операций векторного анализа.
f=x^2+x y^2+x y z^2;g=Exp[xyz];h=Sin[xyz];
gradient[f, {x,y, z}]
{2x+y2+yz2, 2xy +xz2, 2xyz}
jacobian[{f,g,h}, {x,y, z} ] //MatrixForm
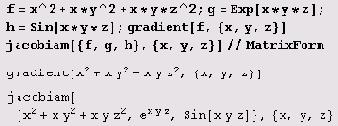
Впрочем, операции векторного анализа приходится выполнять не только в декартовой системе координат. Поэтому для выполнения этих операций имеется специальный пакет, загружаемый как обычно: <<Calculus`VectorAnalysis`. В нем предусмотрено выполнение операций в самых разнообразных системах координат — декартовой, цилиндрической, сферической, параболической, тороидальной, бисферической, сфероидальной, биполярной, параболоидной, эллиптической, эллипсоидной и т.д.
По умолчанию устанавливается декартова система координат. Вот как определить установленную систему координат и название ее переменных.
{CoordinateSystem,Coordinates[]}
{Cartesian,{Xx,Yy,Zz}}
Вот как вычислить градиент.
Grad[Xx+Sin[YyZz]] {l,Zz Cos[YyZz],Yy Cos[YyZz]}
Систему координат и название переменных можно изменить.
SetCoordinates[Cartesian[х,у,z]] Cartesian[x,у,z]
Мы установили декартову систему координат, но изменили название переменных. Посчитаем дивергенцию.
Div[{x y,x у z,Sin[x у z]}]
у+х z+x у Cos[х у z]
Установим теперь сферическую систему координат.
SetCoordinates[Spherical[r,th,ph]] Spherical[r,th,ph]
Узнаем промежутки изменения координат.
CoordinateRanges[] (0<r<∞, 0<th<π, -π<ph<π}
Напишем формулы преобразования координат.
CoordinatesToCartesian[[r,th,ph)]
{r Cos[ph] Sin[th],r Sin[ph]
Sin[th],r Cos[th]}
Найдем якобиан.
jdet=JacobianDeterminant[]
r2 Sin [th]
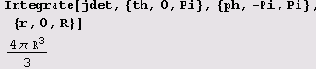
Шутки ради вычислим площадь поверхности сферы радиуса R
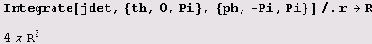
и объем сферы радиуса R:
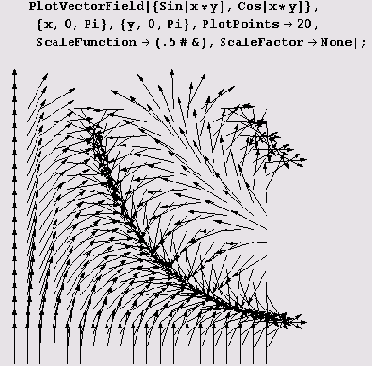
При решении многих задач весьма полезно изображать векторные поля графически. Для изображения двухмерных полей следует подгрузить пакет <<Graphics` PlotField`. Вот как с его помощью можно изобразить двухмерное поле.
Не сложнее нарисовать и градиент скалярного поля.

Есть и функции для вычерчивания полей, заданных таблично.
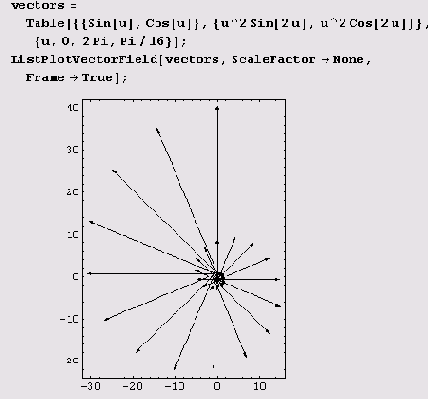
Для трехмерных полей нужно загружать пакет <<Graphics `PlotField3D`
Вот как можно нарисовать векторное поле, компоненты которого равны y/z, -x/z и 0.

Есть, конечно, и функция для изображения градиента скалярной функции. Ниже изображен градиент функции xyz.

Эти средства изображения векторных полей могут применяться, конечно, не только в векторном анализе, но и для решения других задач, например для исследования дифференциальных уравнений.