Теория универсальности, или насколько сложным может быть поведение простой динамической системы

Возможно, заголовок кажется вам заумным. Может быть, это просто оттого, что вы никогда не слышали о динамических системах. Не беспокойтесь, все очень просто: в данном случае под динамической системой понимается любая система, в которой некоторый параметр определяется рекуррентным уравнением х_n+1 =f(x_n, r). В частности, под динамической системой можно понимать числовую последовательность, определяемую таким уравнением. Где встречаются такие последовательности? Да почти повсюду. Вот простейший пример.

Допустим, нас интересует изменение численности какого-либо вида животных в определенном районе. Один раз в год мы считаем их и получаем число х. По этим данным можно построить последовательность x1, х2 ..., хn, ... (n = 1 соответствует первому измерению). Логично предположить, что среди этих чисел есть какая-то закономерность. Естественно ожидать, что численность популяции в (n+1)-й год х_n+1 зависит от того, сколько животных было год назад, т. е. от величины х_n. Поэтому в простейшем случае х_n+1 = f(x_n, r).

Здесь f— непрерывная функция; r— некий параметр, который зависит от биологических особенностей рассматриваемого вида. В популяционной генетике часто предполагается, что х_n+1 = rx_n(N-x_n).

Эта формула показывает, что численность вида быстро растет, пока она мала (x_n<N), и начинает убывать, когда животных становится слишком много. Если сдeлать замену переменных х_n = x'_nN, r = r'/N, то в новых переменных наше уравнение будет иметь вид х'_n+1 = г' х'_n(1—х'_n). Тем самым мы элиминировали параметр N и привели уравнение к более естественной для математиков форме. Теперь по самому смыслу задачи 0<х'_n<1. Простоты ради опустим штрихи и займемся исследованием этой более простой динамической последовательности.

Что же будет происходить с различными видами (т.е. с последовательностями х_n+1 = rх_n(1— х_n) с различными r) по прошествии достаточно долгого времени? Чтобы ответить на этот вопрос для нашей простейшей модели, достаточно выяснить, как будет вести себя последовательность {х_n} при различных значениях г. Давайте проведем численный эксперимент. Сначала дадим нужные нам определения.

х[r_][0]=0.5;

 x[r_][n_]:=x[r1[n]=r х[r][n-1]<1-х[r][n-1])

Таким образом, мы задали начальный член последовательности х₀ = 0,5. Теперь положим, r = 3,83, и вычислим первые пятьдесят членов последовательности.

Вот как все это выглядит на графике.

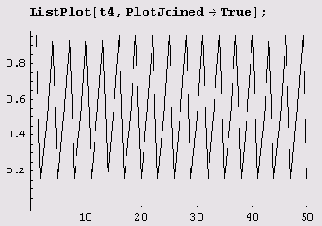
Вот теперь действительно есть чему удивиться! Численность популяции оказалась периодической функцией.

Конечно, здесь проведены вычисления только дляr = 3,83, а нам нужно провести вычисления для разных r. Давайте проведем их для 250 значений г, равномерно распределенных между r = 2,8 и r = 4,0.

t1=Table[{r,x[r][n]},{r,2.8,4,1.2/249},{n,101,300}];

Здесь для каждого из 250 значений г строится список х_n для n- 101, ..., 300. Вот что получается (конец опущен).

Чтобы построить график, этот список нужно сделать плоским:

toshow=Flatten[t1,1);

Теперь список будет иметь вид (конец опущен)

{{2.8,0.642857},{2.8,0.642857},{2.8,0.642857},{2.8,0.642857},

{2.8,0.64 2857},{2.8,0.642857},{2.8,0.642857},{2.8,0.642857},

и мы можем построить график, наглядно демонстрирующий поведение последовательности {*„} при различных значениях параметра г в отображении х_n+1= rх_n(1-х_n).

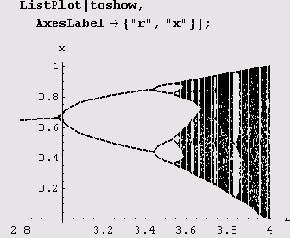
Из графика видно, насколько сложно зависит поведение популяции от r.

Еще раз обратим внимание на простенькую формулу х_n+1 = rх_n(1-х_n). При небольших г (0<r<1) х_n стремится к нулю независимо от выбора XQ. Судя по формуле хn+1= rx_n(1-х_n), вид, численность которого вначале равна XQ, выжить не может, сколько бы животных ни было вначале. Поведение последовательности в этом и в других случаях удобно представлять графически. Нарисуем кривую y=f(x) при заданном значении г и прямую у = х. Отложим х по оси абсцисс, проведем вертикаль до пересечения с кривой у —/(х) (точка А), а затем из точки пересечения горизонталь до пересечения с линией у = х (точка В). Теперь вновь проведем вертикаль до пересечения с кривой у = f(x), что даст нам точку С с координатой х₂. Тогда х₂ =f(х₁). Взяв точку х₂ за начальную и повторив все те же операции, получим х₃, затем х₄ и т.д.

Теперь рисуем график, чтобы представить поведение последовательности х_nпри n->∞.

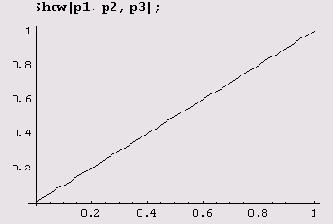
Из рисунка видно, что х_n->0 при n->∞.

Из формулы х_n+1 = rхn(1-хn) следует, что функция f(x) переводит отрезок [0, 1] в отрезок [0, r/4]. Если r<4, то все значения х„ лежат на отрезке [0, 1] при условии, что 0<х<1. Так что формула х_n+1 = rхn(1—хn) задает отображение отрезка [=, 1] в себя.

Пусть теперь r немного больше 1, например r = 2.

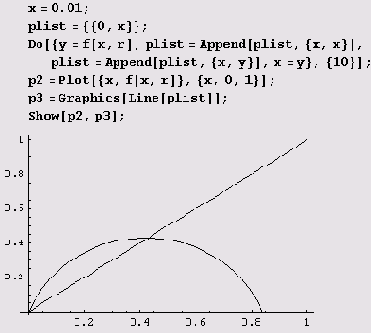
Видим, что при этом значении г последовательность {хn} ведет себя по-другому: хn стремится к постоянному, отличному от нуля, значению хn при n—>∞. В применении к исходной биологической задаче это означает, что численность такого вида по прошествии нескольких лет стабилизируется и перестанет меняться со временем.

Значение х* может быть найдено из уравнения х* = f(x*).

Все точки, удовлетворяющие этому уравнению, являются неподвижными точками функции f, так как если х, = х', то и х2 = х', хn = х' при любом n.

При r<1 квадратное уравнение х=rх(1- х) имеет один неотрицательный корень х=*0. При t->1 неотрицательных корня два: х* = 0 nх* = (t-1)/r. При r= 1 происходит бифуркация: неподвижная точка х' = 0 теряет устойчивость, а вновь появившаяся точка становится устойчивой.

Можно довольно просто определить, будет ли устойчивой неподвижная точка х отображения f[x]. Пусть х„ = х + Δхn, где Δхn — малое число. Если точка устойчива, то с ростом n величина |Δхn| должна уменьшаться. Перепишем формулу х_n+1 = f(xn, r) в виде

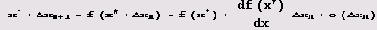
Если в последнем равенстве опустить член о(Δхn), то полученное приближенное равенство будет выполняться тем точнее, чем меньше Δхn (мы пренебрегли членами, пропорциональными (Δхn)², (Δхn)³ и т.д.). Поскольку x* = f(x), то

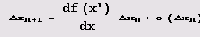
И для того чтобы Δх_n+1->0 при n->∞, должно выполняться неравенство

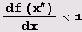
Это и есть условие устойчивости точки х*.

Будем дальше увеличивать параметр r. Поведение системы снова изменится: в последовательности {хn}, начиная с достаточно больших и, будут чередоваться числа, близкие к некоторым двум числам я, и а2. (Точнее говоря, последовательность устроена так, что x_2n+1->a₁, х_2n+1->n₂ при n->∞) Эти числа связаны соотношениями а1 = f(а₂), а₂ = f(а₁). Иными словами, в этом случае отображение х_n+1 = rхn(1—хn) имеет устойчивый цикл с периодом 2. Обозначим этот цикл 52. Наличие цикла S* в нашей модели означает, что численность популяции будет меняться с периодом в 2 года.

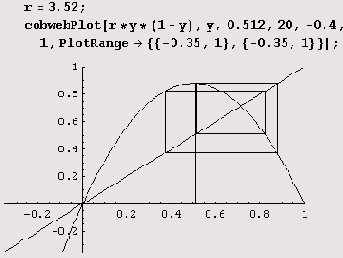
Выясним, как выглядят циклы на графике. Для этого определим программу cobwebPlot.

Сначала протестируем эту программу.

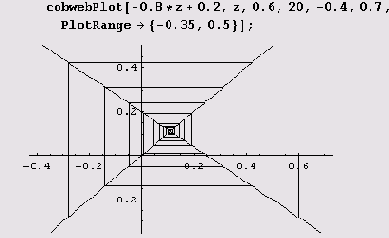
Теперь нарисуем картинку для случая г = 1.

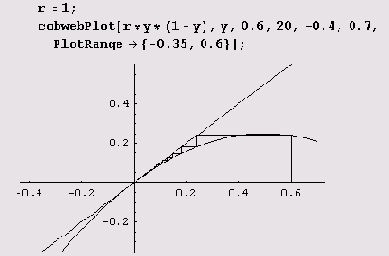
Теперь нарисуем картинку для случая г = 2.

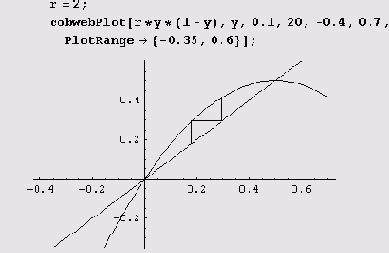
Наконец, выясним, как выглядит двойной цикл (цикл с периодом 2).

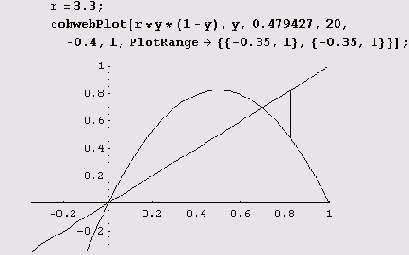
Переход от неподвижной точки, которую можно считать циклом S1, к циклу 52 произошел в результате бифуркации, которая получила название бифуркации удвоения периода. Точка х при этом не исчезла и осталась неподвижной, однако величина

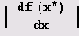
При дальнейшем увеличении г поведение последовательности {хn} опять изменяется. Возникает цикл S⁴: х_4n->а₁, x_4n+1->a₂, х_4n+1->a₃> x_4n+3->а₄ ПРИ n->∞, причем а2 = f(a1), а3=f(a2), аn =f(an). Численность популяции начинает колебаться с периодом в 4 года.

Но и это еще не все. Приведем еще несколько примеров поведения наших последовательностей.

Последовательно увеличивая значение параметра, мы увидим циклы S⁸, S¹⁶, S³² и т.д. При этом каждый раз цикл S² теряет устойчивость, и устойчивым становится цикл S² . Наконец, при некотором значении г (его иногда обозначают г„) формула x_n+1 = rхn(1-хn) дает уже непериодическую последовательность {xn}.

Полученная нами картина оказалась очень интересной. Во-первых, в поразительно простой модели х_n+1 = rхn(1-хn) заложено очень сложное поведение. Во-вторых, в ней удается проследить большое количество бифуркаций, приводящих к усложнению решения. Сделать это в более сложных моделях гораздо труднее. Как это ни удивительно, но пока встречались только циклы, период которых равен степени 2.

Чтобы понять, чем это вызвано, и изучить поведение модели более подробно, наряду с функцией f(x) удобно рассмотреть отображение f(f(х)), обозначаемое далее через f²(х), и вообще положить f^n+l(x) =f(fⁿ(x)), считая, конечно, что f(n) =f(х).

Построим график f(x).

Вот нужные нам определения.

f[х_,r_]:=г*х*(1-х);

ff[x_,r_,n_]:=Module[{t=x},Do[{t=f[x,r],x=t},{n}];t]

Сначала рассмотрим случай устойчивой неподвижной точки. Вот что получим для случая г = 3.

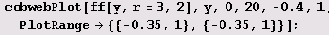
Теперь рассмотрим случай устойчивого цикла S².

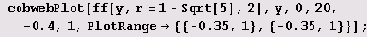
График функции f(x) пересекается с прямой у = х во всех неподвижных точках отображения / (ведь для любой неподвижной точки х отображения f имеем f²(х*) = f(f(x')) = f(x') = (х'), а также в точках, принадлежащих циклам 52 (потому что а2 = f(a1) = f(f(a2)) и а1 = f(a2) = f(f(f()))- Увеличивая параметр r, мы растягиваем функцию f(x) вдоль оси у. И если при некотором значении г линии у = х и у = fix) пересекаются в одной точке, то с увеличением г могут появиться еще две точки пересечения. Они-то и будут определять цикл S2.

Таким образом, переход от 51 к 52 в отображении f(x) обусловлен тем, что в отображении f (х) одна из неподвижных точек теряет устойчивость и в ее окрестности появляются две новые устойчивые неподвижные точки. Здесь вновь происходит бифуркация. Рассматривая функции f⁴(х), fⁿ(x) и так далее, можно посмотреть, как происходят следующие удвоения.

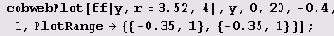
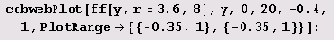
На примере модели х_n+1 = rхn(1- хn) можно понять не только качественные, но и удивительные количественные закономерности. Чтобы проследить за ними, построим график х(r): по оси х будем откладывать х₁, х₂, ..., лежащие на устойчивом цикле, по оси г — значения параметра. Циклу S* будут соответствовать две точки на одной вертикали, циклу S1 — четыре и т.д. Тогда получим ранее приведенный график, отражающий усложнение устойчивых циклов в отображении х_n+1 = rхn(1-хn), происходящее в результате бифуркаций удвоения периода.

Обозначим через R1, R2, R}, ... те значения параметра г, в которых происходили удвоения, а через r1, r2, г3, ... — значения параметра, при которых х= 1/2 является элементом цикла S2, S4, Ss и т. д. Введем также величины d1, d2, ..., dn, .., равные расстоянию между х = 1/2 и ближайшим к нему элементом цикла S² при r = r_n. Расчеты показали, что числа f(x) и r_n при больших и ведут себя как геометрическая прогрессия со знаменателем a = 4,6692016... Другими словами,

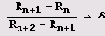
d_n/d_n+1 также имеет предел, равный некоторому числу а, причем а = 2,5029078...

Что будет, если вместо функции х_n+1 = rхn(1—х_n) взять любую другую симметричную функцию, которая имеет на отрезке [О, 1] один максимум и около вершины близка к квадратичной параболе. Пусть в ней также происходит бесконечная последовательность бифуркаций удвоения при изменении некоторого параметра. Оказалось, что в любой такой модели числа а и 5S будут одними и теми же! Более того, независимо от вида функции предел lim(-a)ⁿf²ⁿ[(x-0,5)/(-a)ⁿ,r_n] существует и будет одной и той же универсальной функцией, обозначаемой часто через g₀(х).

Эти удивительные закономерности были обнаружены и поняты американским математиком М. Фейгенбаумом в 1978 году. В силу универсальности чисел а и 5 и функции g₀(x), a также других функций такого типа эту теорию называют теорией универсальности.

Что же означают эти результаты?

В природе можно выделить два совершенно различных на первый взгляд типа явлений. Одни — регулярные и упорядоченные. Это большинство процессов, используемых в технике и технологии, процессы, в которых возникают структуры. Как правило, ход таких процессов можно предсказывать, зная управляющие ими законы.

Другие процессы — случайные, хаотические. К ним относится турбулентное движение жидкости, шумы в различных электронных системах и т.д. Они требуют другого, статистического описания, которое позволяет получить некоторые усредненные характеристики процессов. Такие явления также очень важны, но используются гораздо реже из-за их сложности и недостаточной изученности. В одних случаях турбулентное движение жидкости позволяет транспортировать уголь, руду и многое другое по трубам. В других — с турбулентными вихрями приходится бороться. Хорошо зная законы турбулентного движения, можно было бы строить более быстрые и экономичные суда и самолеты.

Теория Фейгенбаума приводит к парадоксальному выводу: между хаосом и порядком есть глубокая внутренняя связь. Непериодический, случайный процесс возникает как предел все более сложных структур (циклов S²ⁿ). Хаос возникает как сверхсложная организация (цикл S² )! Этот вывод является очень общим: он может относиться к моделям экологии, гидродинамике — к любым системам, где есть последовательность бифуркаций удвоения периода.

Возможно, вы подумали, что сложность взаимоотношений порядка и хаоса, имеющая место в данной модели, связана с участием вещественных чисел. Тогда вспомните график функции Эйлера, график количества единиц в двоичной записи целых чисел. На этих графиках, где нет ничего, кроме целых чисел, также наблюдается сложная картина чередования хаоса и циклов.

Еще более сложная .картина может наблюдаться в многомерном (например, в двухмерном) случае. Если модель к тому еще и дискретная, то можно говорить о клеточных автоматах.
Содержание раздела