Алгебра и пакет Mathematica 5
Электронная https://diploma-russian.com/kupit-attestat-shkolyi-11-klassov подача заявки на аттестат.
Клеточные автоматы
Клеточный автомат — это совокупность клеток пространства (возможно, многомерного), каждая из которых может находиться в одном из нескольких состояний. Клеточные автоматы представляют собой дискретную модель, основанную на рекуррентных правилах: следующий шаг является результатом применения правил к конфигурации, достигнутой на предыдущем шаге. Вот как эволюционирует Вселенная (иногда ее удобно рассматривать тоже как клеточный автомат), населенная такими автоматами. Все пространство (Вселенная) разбито на клетки, каждая из которых может находиться в одном из нескольких состояний. (Сами клетки тоже можно рассматривать как простейшие автоматы. Тогда можно сказать, что в некоторых клетках "живут" простейшие автоматы.) Эти клетки (простейшие автоматы) подчиняются определенным правилам (законам населяемой ими Вселенной). Сами правила обычно настолько просты, что могут быть занумерованы числами. Однако получающиеся в результате жизнедеятельности таких организмов конфигурации могут быть очень сложными. Иными словами, сообщество примитивных организмов (т.е. организмов, живущих по весьма примитивным правилам) может создать весьма сложную социальную структуру. Возможна и другая трактовка: хотя сами элементарные частицы устроены просто и подчиняются весьма простым законам, они образуют нашу Вселенную. (Разумеется, Вселенная устроена весьма сложно.)
Чтобы увидеть все это на экране, нам понадобится предварительно познакомиться с несколькими функциями. Функция
CellularAutomaton [правило, начальная конфигурация, число шагов] генерирует представление (список) конфигурации, в которую переходит начальная конфигурация после указанного числа шагов в соответствии с заданным правилом. Функция
Raster [{{а11, а12, ... }, ... }] является двухмерным графическим примитивом, который представляет прямоугольный массив ячеек в градациях серого. (Состояние клетки удобно изображать определенным цветом или градацией серого.) Вот пример.

Конечно, рисунок, особенно при большом числе клеток, может выглядеть и более замысловато.
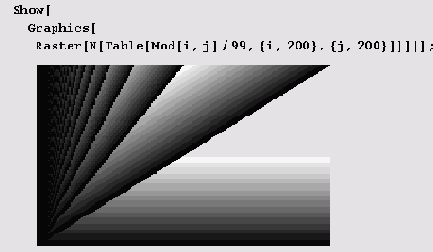
-это уже нечто вроде приглашения в театр, где актерами будут клеточные автоматы. Но вначале увертюра. Нам понадобится еще одна функция.
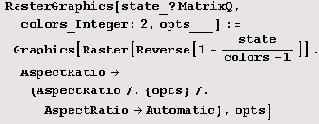
Теперь используем правило 481, и занавес поднят!

Естественно, здесь мы видим только конечный результат. Давайте теперь посмотрим, как эволюционирует Вселенная с одним единственным атомом (число 1), окруженным пустотой (нулями) по правилу 30. Вот начальное состояние:
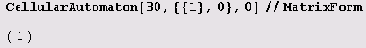
А вот та же Вселенная через три секунды (секунда = 1 шаг):
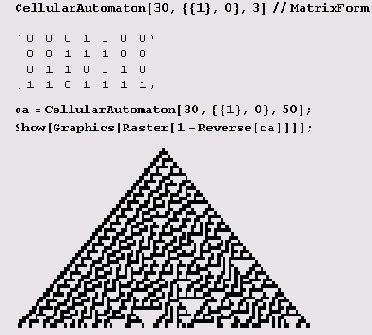
Здесь, правда, для удобства наблюдателей, приведен негатив Вселенной, притом перевернутый!
Отвечая на вопрос Наполеона о необходимости Создателя, можно сказать, что если у этой Вселенной и был Создатель, то им был Стив Вольфрам!
Несомненно, самым известным двухмерным клеточным автоматом является игра "Жизнь", придуманная Джоном Конвеем в 1970 году. Именно она прославилась своими многочисленными узорами и способностью заставлять людей тратить уйму машинного времени на поиски еще более интересных узоров! В этой игре с очень простыми правилами есть все: катапульты, ружья, паровозы, планеры, циклы, пожиратели планеров, крокодилы, стационары, семафоры и аннигиляция. Крокодил, например, является пожирателем планеров, поскольку он проглатывает планер без всякого ущерба для себя. С помощью функции
CellularAutomaton вы можете разыграть захватывающие сценки из этой Вселенной!
А если клетки в придуманной вами Вселенной будут достаточно малыми, а процесс эволюции — достаточно длительный (например, 80 шагов), вы можете увидеть самоподобные конфигурации, и тогда вспомните о фракталах, множествах Мандельброта и Жулиа! Для обстоятельного разговора о них, конечно, нужна отдельная книга, и, возможно, не одна. Ну а мы, кратко обсудив в главе 1 применение системы Mathematica к изучению фракталов, теперь завершили своеобразный цикл 5" (очень редкий — с нечетным показателем!), ведь эта глава — одиннадцатая. И последняя — в этой книге. И если ваше знакомство с системой Mathematica продолжится, я считаю, вы прочли эту книгу недаром. Ну а сейчас пришло время сказать, как это знакомство продолжить. Иными словами, сейчас я собираюсь вкратце перечислить хотя бы некоторые ресурсы по системе Mathematica и по ходу дела указать на то, что осталось "за кадром".