Матричные вычисления в Mathcad
         

Фурьеспектр действительных данных



14.1.1. Фурье-спектр действительных данных



Преобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм, называемый БПФ (быстрое преобразование Фурье). Рассмотрим сначала наиболее типичную для физического эксперимента ситуацию расчета Фурье-спектра действительного сигнала, для которой алгоритм БПФ реализован в нескольких встроенных функциях Mathcad, различающихся нормировками:

fft (у) — вектор прямого преобразования Фурье;  FFT (у) — вектор прямого преобразования Фурье в другой нормировке:

 у — вектор действительных данных, взятых через равные промежутки значений аргумента.


ВНИМАНИЕ!

Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно 2n элементов (n— целое число). Результатом является вектор с 1+2n-1 элементами. Если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями, иначе вместо решения появится сообщение об ошибке.



Встроенная функция вейвлетпреобразования



14.2.1. Встроенная функция вейвлет-преобразования





Mathcad имеет одну встроенную функцию для расчета вейвлет-преобразования на основе вейвлетобразующей функции Добеши:

wave (у) — вектор прямого вейвлет-преобразования;  iwave (v) — вектор обратного вейвлет-преобразования:

 у — вектор данных, взятых через равные промежутки значений аргумента;  v — вектор данных вейвлет-спектра.


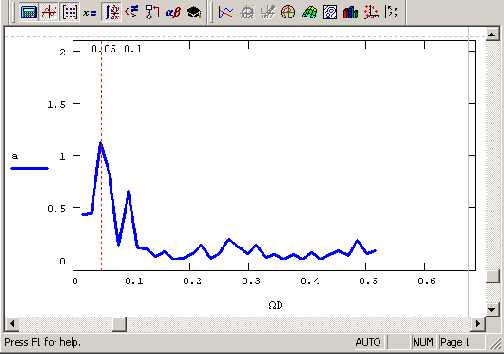
Аргумент функции вейвлет-преобразования, т. е. вектор у, должен так же, как и в преобразовании Фурье, иметь ровно 2n элементов (n — целое число). Результатом функции wave является вектор, скомпонованный из нескольких коэффициентов с двухпараметрического вейвлет-спектра. Использование функции wave объясняется на примере анализа суммы двух синусоид в листинге 14.5, а три семейства коэффициентов вычисленного вейвлет-спектра показаны на Рисунок 14.16.



Встроенные функции для сглаживания ВЧфильтр



14.3.1. Встроенные функции для сглаживания: ВЧ-фильтр



В Mathcad имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных:

medsmooth(y,b) — сглаживание алгоритмом "бегущих медиан";  ksmooth (х, у, b) — сглаживание на основе функции Гаусса;  supsmooth(x,y) — локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных:

 х — вектор действительных данных аргумента (для supsmooth его элементы должны быть расположены в порядке возрастания);  у — вектор действительных значений того же размера, что и х;  b — ширина окна сглаживания.


Все функции имеют в качестве аргумента векторы, составленные из массива данных, и выдают в качестве результата вектор сглаженных данных того же размера. Функция medsmooth предполагает, что данные расположены равномерно.

Примечание 1
Примечание 1

Подробную информацию об алгоритмах, заложенных в функции сглаживания, вы найдете в справочной системе Mathcad в статье Smoothing (Сглаживание), находящейся в разделе Statistics (Статистика). Очень полезные сведения о разных типах фильтрации можно отыскать в Быстрых шпаргалках.



Часто бывает полезным совместить сглаживание с последующей интерполяцией или регрессией. Соответствующий пример приведен в листинге 14.7 для функции supsmooth. Результат работы листинга показан на Рисунок 14.18 (кружки обозначают исходные данные, крестики — сглаженные, пунктирная кривая — результат сплайн-интерполяции). Сглаживание тех же данных при помощи "бегущих медиан" и функции Гаусса с разным значением ширины окна пропускания показаны на Рисунок 14.19 и 14.20 соответственно.



Обратное преобразование Фурье



14.1.2. Обратное преобразование Фурье



Для расчета обратного Фурье-преобразования (восстановления сигнала по имеющемуся действительному спектру) следует использовать следующие встроенные функции (они также реализуют алгоритм БПФ):

ifft (v) — вектор обратного действительного преобразования Фурье;  IFFT(V) — вектор обратного действительного преобразования Фурье в другой нормировке:

 v — вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.


Примечание 1
Примечание 1

Аргумент (вектор v) функций, реализующих обратное преобразование Фурье, может быть как действительным, так и комплексным. А вот результат их работы является вектором, составленным из действительных чисел. Если аргумент является N-компонентным вектором, где N=l+2n, то в результате получается в два раза больший вектор из 2 (N-1) =2n+1 компонент.



Результат обратного преобразования Фурье спектра, представленного на Рисунок 14.2 и 14.3, показан в виде кружков на Рисунок 14.5 вместе с исходными данными.



Программирование вейвлетпреобразований



14.2.2. Программирование вейвлет-преобразований



Наряду со встроенной функцией wave Mathcad снабжен пакетом расширения для осуществления вейвлет-анализа. Пакет расширения содержит большое число дополнительных встроенных функций, имеющих отношение к вейвлет-преобразованиям. Обзор пакетов расширения выходит за рамки данной книги, поэтому ограничимся простым упоминанием об этой возможности. Напомним, что дополнительную информацию об использовании данных встроенных функций можно найти в соответствующей электронной книге, которую можно открыть при помощи меню Help / E-Books / Wavelet extension pack (Справка / Электронные книги / Вейвлет-анализ данных).

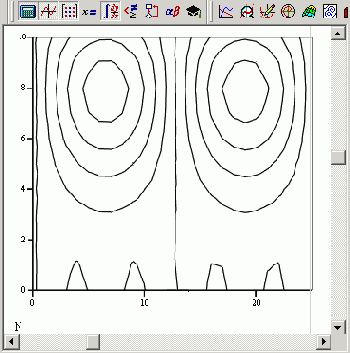
Помимо встроенной функции вейвлет-спектра Добеши и возможностей пакета расширения Mathcad, возможно непосредственное программирование алгоритмов пользователя для расчета вейвлет-спектров. Оно сводится к аккуратному расчету соответствующих семейств интегралов. Один из примеров такой программы приведен в листинге 14.6, а ее результат на Рисунок 14.17. Анализу подвергается та же функция, составленная из суммы двух гармонических функций, сильно различающихся по частоте. Сам график двухпара-метрического вейвлет-спектра с(а,b) на плоскости (а,b) выведен в виде привычных для вейвлет-анализа линий уровня.



Скользящее усреднение ВЧфильтр



14.3.2. Скользящее усреднение: ВЧ-фильтр



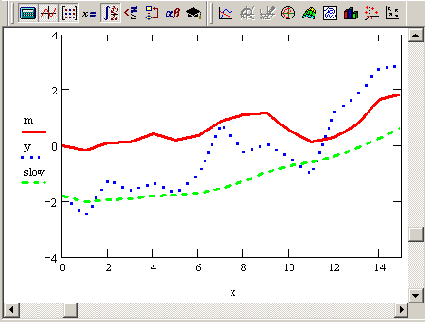
Помимо встроенных в Mathcad, существует несколько популярных алгоритмов сглаживания, на одном из которых хочется остановиться особо. Самый простой и очень эффективный метод — это скользящее усреднение. Его суть состоит в расчете для каждого значения аргумента среднего значения по соседним w данным. Число w называют окном скользящего усреднения; чем оно больше, тем больше данных участвуют в расчете среднего, тем более сглаженная кривая получается. На Рисунок 14.21 показан результат скользящего усреднения одних и тех же данных (кружки) с разным окном w=3 (пунктир), w=5 (штрихованная кривая) и w=l5 (сплошная кривая). Видно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w — отражают лишь закономерность их медленных вариаций.



Преобразование Фурье комплексных данных



14.1.3. Преобразование Фурье комплексных данных



Алгоритм быстрого преобразования Фурье для комплексных данных встроен в соответствующие функции, в имя которых входит литера "с":

cfft (у) — вектор прямого комплексного преобразования Фурье;  CFFT(y) — вектор прямого комплексного преобразования Фурье в другой нормировке;   icfft(y) — вектор обратного комплексного преобразования Фурье;  ICFFT(V) — вектор обратного комплексного преобразования Фурье в другой нормировке:

 у — вектор данных, взятых через равные промежутки значений аргумента;  v — вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.


Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля, и выводят только его половину (см. разд. 14.1. Г). Поэтому, в частности, по 128 действительным данным получалось всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье (Рисунок 14.6), то получится вектор из 128 элементов. Сравнивая Рисунок 14.3 и 14.6, можно уяснить соответствие между результатами действительного и комплексного Фурье-преобразования.



Устранение тренда НЧфильтр



14.3.3. Устранение тренда: НЧ-фильтр



Еще одна типичная задача возникает, когда интерес исследований заключается не в анализе медленных (или низкочастотных) вариаций сигнала у(х) (для чего применяется сглаживание данных), а в анализе быстрых его изменений. Часто бывает, что быстрые (или высокочастотные) вариации накладываются определенным образом на медленные, которые обычно называют трендом. Часто тренд имеет заранее предсказуемый вид, например, линейный. Чтобы устранить тренд, можно предложить последовательность действий, реализованную в листинге 14.9.

1. Вычислить регрессию f (х), например, линейную, исходя из априорной информации о тренде (предпоследняя строка листинга).

2. Вычесть из данных у(х) тренд f (х) (последняя строка листинга).



Полосовая фильтрация



14.3.4. Полосовая фильтрация



В предыдущих разделах была рассмотрена фильтрация быстрых вариаций сигнала (сглаживание) и его медленных вариаций (снятие тренда). Иногда требуется выделить среднемасштабную составляющую сигнала, уменьшив как более быстрые, так и более медленные его компоненты. Одна из возможностей решения этой задачи связана с применением полосовой фильтрации на основе последовательного скользящего усреднения.

Алгоритм Полосовой фильтрации приведен в листинге 14.10, а результат его применения показан на Рисунок 14.23 сплошной кривой. Алгоритм реализует такую последовательность операций:

1. Выставление ноль-линии, т. е. приведение массива данных у к нулевому среднему значению путем его вычитания из каждого элемента у (третья и четвертая строки листинга).

2. Устранение из сигнала у высокочастотной составляющей, имеющее целью получить сглаженный сигнал middle, например, с помощью скользящего усреднения с малым окном w (в листинге 14.10 w=3).

3. Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном w (в листинге 14.9 w=7), либо с помощью снятия тренда (см. разд. 14.3.3).

4. Вычесть из сигнала middle тренд slow (последняя строка листинга), тем самым выделяя среднемасштабную составляющую исходного сигнала у.



Пример артефакты дискретного Фурьепреобразования



14.1.4. Пример: артефакты дискретного Фурье-преобразования



При численном нахождении преобразования Фурье следует очень внимательно относиться к таким важнейшим параметрам, как объем выборки (в терминах листинга 14.1, xМАХ) и интервал дискретизации (?). Соотношение этих двух величин определяет диапазон частот (?0,?N), для которых возможно вычисление значений Фурье-спектра. В этой связи хотелось бы обратить внимание на три типичные опасности, которые могут подстерегать неподготовленного исследователя при расчете дискретного Фурье-преобразования и быть для него весьма неожиданными.

Влияние конечности интервала выборки

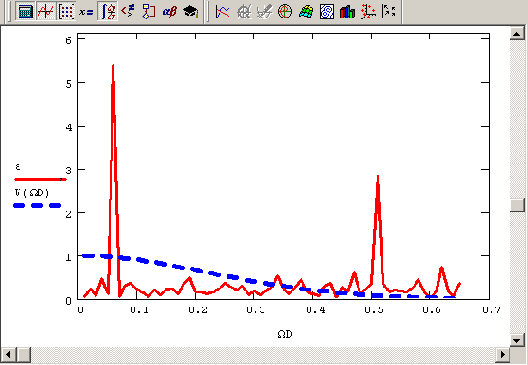
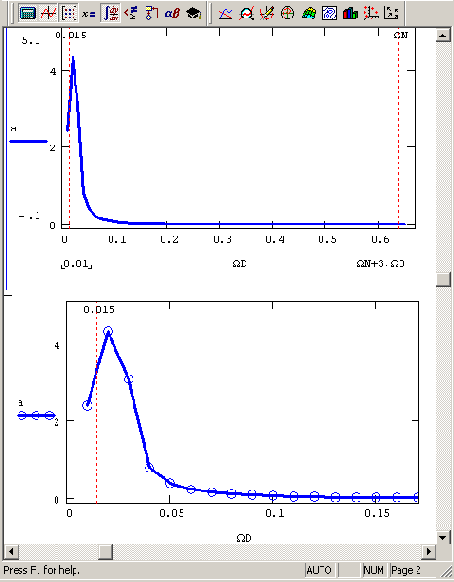
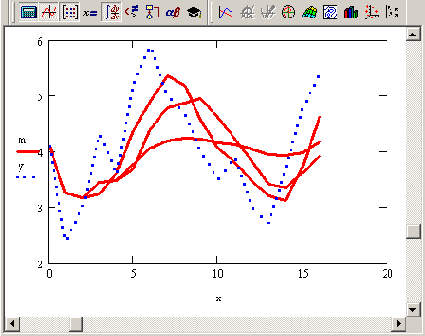
Во-первых, следует обратить внимание на само определение преобразования Фурье как интеграла с бесконечными пределами. Его численное отыскание подразумевает принципиальную ограниченность интервала интегрирования (просто в силу конечности объема выборки). Поэтому самым очевидным несоответствием будет поиск, вообще говоря, другого интеграла, отличного от интеграла Фурье. Влияние конечности интервала выборки проявляется главным образом на искажении его низкочастотной области. В качестве примера приведем Фурье-спектр гармонической функции с частотой 0.015. Для его расчета достаточно заменить в листинге 14.1 четвертую строку на равенство yi:=sin(2?0.915xi). Соответствующий Фурье-спектр изображен на Рисунок 14.7 (сверху — в обычном, а снизу — в более крупном масштабе) и демонстрирует не совсем правильное поведение в низкочастотной области. Как видно, спектр содержит довольно широкий максимум вместо одиночного пика, как было в случае средних частот сигнала на Рисунок 14.3.

Примечание 1
Примечание 1

Если быть точным, вместо спектра некоторой функции f (х) дискретное преобразование Фурье подразумевает вычисление спектра другой функции f (х)Ф(х), где Ф(х) — это функция-ступенька, равная единице в пределах расчетного интервала и нулю за его пределами. В частотной области это соответствует операции свертки означенных двух функций, что, конечно, искажает (неизвестный) точный спектр f (х). Для борьбы с проявлением конечности интервала выборки используются специальные методы, основанные на применении техники спектральных окон.



Примечание 2
Примечание 2

Из сказанного ясно, почему исследователя не должна смущать необходимость дополнения массива исходных данных нулями до размера 2" (чтобы можно было использовать алгоритм БПФ). По самому определению дискретного Фурье-преобразования, исходная функция и так предполагается равной нулю за пределами расчетного интервала, что приводит к неминуемым искажениям.



Пример спектр модели сигнал/шум



14.1.5. Пример: спектр модели сигнал/шум



Пока мы использовали в качестве примера детерминированный сигнал, представляющий собой сумму трех синусоид. Несмотря на единство термина "дискретное преобразование Фурье", прикладное применение спектрального анализа можно довольно четко разделить на две категории.

Сигнал, подвергающийся спектральному анализу, получен в условиях пренебрежимо малой погрешности, т. е. его можно, фактически, считать детерминированным. Такая ситуация характерна для экспериментальной оптики и (разного рода) спектроскопии. В этом случае для большинства задач анализа сигналов бывает вполне достаточно использовать простые спектры Фурье, рассмотренные выше (см. разд. 14.1.1—14.1.3).  Сигнал, полученный в присутствии значительной шумовой компоненты, которая существенно искажает его структуру. В этом случае следует говорить о смеси (к счастью, чаще всего аддитивной) "полезный сигнал +  шум", причем в большинстве случаев заранее известна некоторая информация о статистике шумовой компоненты. Данная ситуация очень часто встречается в экспериментальной геофизике и радиофизике. В этом случае подходить к интерпретации спектров следует с вероятностной точки зрения. Как раз этому вопросу мы и посвятим данный пример.


Фурье-спектр

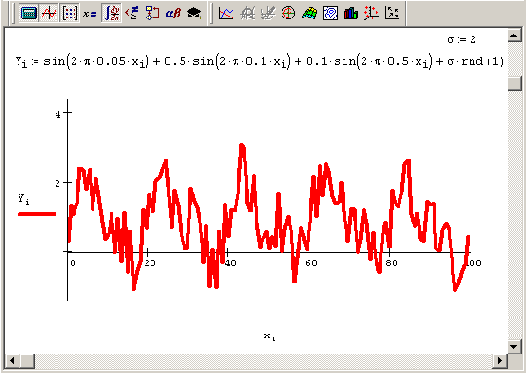
Внесем минимальное добавление в расчеты листинга 14.1, а именно добавим к его четвертой строке (в которой определяется yi) еще одно (четвертое) слагаемое: псевдослучайную величину ?rnd(1), где значение 1/? характеризует отношение сигнал/шум. Явный вид изменений, которые следует внести в листинг 14.1, приведен на Рисунок 14.10, наряду с графиком сигнала у(х). Расчет Фурье-спектра данного сигнала (в соответствии с алгоритмом, представленным выше, см. листинг 14.1) показан на Рисунок 14.11. Как видно, присутствие шумовой компоненты может значительно искажать спектр сигнала и затруднять его интерпретацию.

Примечание 1
Примечание 1

Максимальное значение спектра на левом крае частотного интервала является ни чем иным, как проявлением искажающего влияния конечности выборки и сдвига ноль-линии (см. разд. 14.1.3), произошедшим из-за внесения шума с математическим ожиданием, равным 0.5.



Спектральная фильтрация



14.3.5. Спектральная фильтрация



Альтернативой всем представленным до сих пор алгоритмам, в частности, методу полосовой фильтрации (см. предыдущий разд.) является фильтрация на основе интеграла Фурье. Пока мы использовали для подавления в сигнале тех или иных частотных диапазонов определенные процедуры, основанные на арифметических преобразованиях. Между тем, для той же цели (правда, с большими вычислительными затратами) можно применять методы Фурье-анализа. Действительно, если вычислить спектр сигнала, удалить из него (или существенно уменьшить) определенные частоты, а затем выполнить обратное преобразование Фурье, то результатом будет фильтрованный сигнал.

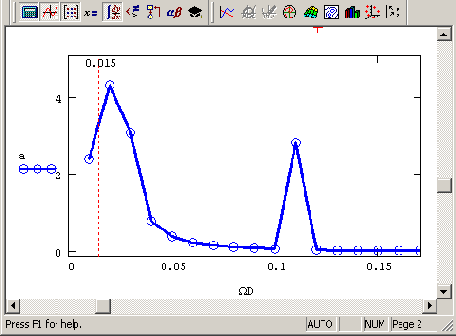
Пример фильтрации на основе преобразования Фурье приведен в листинге 14.11. В качестве модельного сигнала использовалась смесь двух гармонических сигналов и равномерно распределенного шума (Рисунок 14.24). Фурье-спектр данных z, вычисленный при помощи встроенной функции fft, показан на Рисунок 14.25.



Двумерный спектр Фурье



14.1.6. Двумерный спектр Фурье



В Mathcad имеется возможность применять встроенные функции комплексного преобразования Фурье не только к одномерным, но и к двумерным массивам, т. е. матрицам. Соответствующий пример приведен в листинге 14.4 и на Рисунок 14.14 в виде графика линий уровня исходных данных и рассчитанного Фурье-спектра.



Пример вычисление спектра мощности



14.3.6. Пример: вычисление спектра мощности



Завершим главу, посвященную спектральному анализу, еще одним примером вычисления спектра мощности (его определение приведено в разд. 14.1.5) модельного сигнала, связанного с использованием его Фурье-спектра. В листинге 14.12 сначала выполняется преобразование Фурье суммы гармонического сигнала и шума (распределенного равномерно), а затем (в трех последних строках листинга) производится его сглаживание путем скользящего усреднения с окном, равным 3. Из курса математической статистики известно, что квадратная степень сглаженного преобразования Фурье может считаться оценкой спектра мощности, и для вычисленного таким образом спектра уже можно применять вероятностные оценки погрешностей его отсчетов. Результаты работы листинга 14.12 (Фурье- и энергетический спектр) показаны на Рисунок 14.26 (кружками и сплошной кривой соответственно).



Адаптивное сглаживание (продолжение листинга 14 7)



Рисунок 14.18. Адаптивное сглаживание (продолжение листинга 14.7)




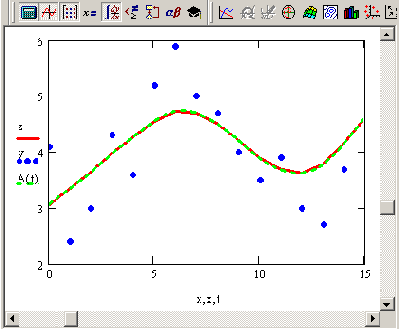
Автокорреляционная функция модельной зависимости сигнал / шум (продолжение листинга 14 3)



Рисунок 14.12. Автокорреляционная функция модельной зависимости сигнал / шум (продолжение листинга 14.3)




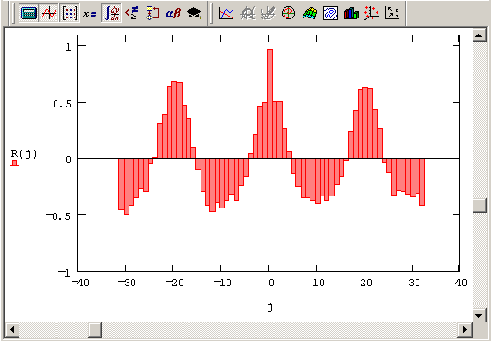
Данные (слева) и их Фурьеспектр (справа) (продолжение листинга 14 4)



Рисунок 14.14. Данные (слева) и их Фурье-спектр (справа) (продолжение листинга 14.4)


 




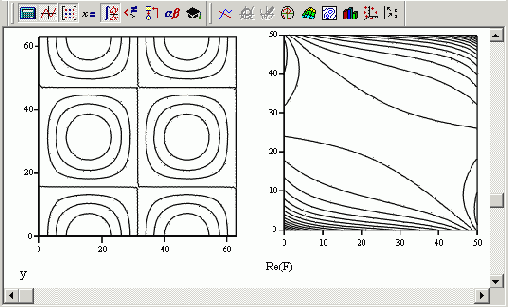
Фурьепреобразование модельного сигнала и его спектр мощности (продолжение листинга 14 12)



Рисунок 14.26. Фурье-преобразование модельного сигнала и его спектр мощности (продолжение листинга 14.12)


 




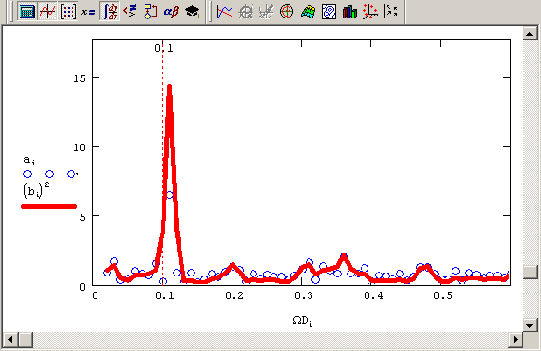
Фурьепреобразование модельного сигнала и спектральное окнофильтр (продолжение листинга 14 11)



Рисунок 14.25. Фурье-преобразование модельного сигнала и спектральное окно-фильтр (продолжение листинга 14.11)


 




Фурьеспектр



14.1. Фурье-спектр



Интегральные преобразования массива сигнала у(х) ставят в соответствие всей совокупности данных у(х) некоторую функцию другой координаты F(v). Рассмотрим встроенные функции для расчета интегральных преобразований, реализованных в Mathcad.

Математический смысл преобразования Фурье состоит в представлении сигнала у(х) в виде бесконечной суммы синусоид вида F(v)sin(v-x). Функция F(V) называется преобразованием Фурье, или интегралом Фурье, или Фурье-спектром сигнала. Ее аргумент v имеет смысл частоты соответствующей составляющей сигнала. Обратное преобразование Фурье переводит спектр F(V) в исходный сигнал у (х). Согласно определению,


Как видно, преобразование Фурье является комплексной величиной, даже если сигнал действительный.

 




Фурьеспектр суммы гармонического сигнала и константы (влияние конечности выборки)



Рисунок 14.8. Фурье-спектр суммы гармонического сигнала и константы (влияние конечности выборки)




Спектральный анализ



Глава 14. Спектральный анализ

Спектральный анализ 14.1. Фурье-спектр 14.1.1. Фурье-спектр действительных данных 14.1.2. Обратное преобразование Фурье 14.1.3. Преобразование Фурье комплексных данных 14.1.4. Пример: артефакты дискретного Фурье-преобразования 14.1.5. Пример: спектр модели сигнал/шум 14.1.6. Двумерный спектр Фурье 14.2. Вейвлет-спектры 14.2.1. Встроенная функция вейвлет-преобразования 14.2.2. Программирование вейвлет-преобразований 14.3. Сглаживание и фильтрация 14.3.1. Встроенные функции для сглаживания: ВЧ-фильтр 14.3.2. Скользящее усреднение: ВЧ-фильтр 14.3.3. Устранение тренда: НЧ-фильтр 14.3.4. Полосовая фильтрация 14.3.5. Спектральная фильтрация 14.3.6. Пример: вычисление спектра мощности
 
Содержание


График Фурьеспектра данных



Рисунок 14.11. График Фурье-спектра данных



Спектр мощности

В силу стохастичности исходных данных, представляющих сумму полезного сигнала и шума, сами вычисленные значения спектра Фурье носят также случайный характер. В этой связи необходимо знать, с какой погрешностью они рассчитываются. Однако из курса математической статистики известно, что для обычного Фурье-преобразования случайного сигнала (в частности, нормального) не найдено оценок для погрешности. Это слабое место Фурье-спектров делает их практически неприменимыми для анализа случайных сигналов, а вместо них надо применять так называемые спектры мощности (или, по-другому, энергетические спектры), для которых указанные оценки существуют.

Не углубляясь в теорию математической статистики, приведем пример вычисления спектра мощности сигнала (Рисунок 14.10), основанный его определении. Как известно, спектром мощности сигнала называют Фурье-преобразование его корреляционной функции. Таким образом, алгоритм расчета спектра мощности сводится к следующему: во-первых, вычислению автокорреляционной функции (Рисунок 14.12); во-вторых, ее прореживанию и (или) сглаживанию (в целях уменьшения влияния конечности выборки); и, наконец, в-третьих, расчету ее Фурье-преобразования. Результат вычисления спектра мощности (листинг 14.3) в соответствии с приведенным сценарием показан на Рисунок 14.13.

Примечание 2
Примечание 2

Аналогичным образом, через Фурье-преобразование взаимной корреляционной функции, определяются взаимные спектры мощности двух выборок.



Примечание 3
Примечание 3

Еще один способ вычисления спектров мощности, не требующий расчета функции корреляции, приведен ниже (см. разд. 14.3.6).



Примечание 4
Примечание 4

Методика расчета в Mathcad корреляционной функции случайного процесса обсуждалась в главе 12 (см. разд. 12.3.3).





График Фурьеспектра данных (продолжение листинга 14 1)



Рисунок 14.3. График Фурье-спектра данных (продолжение листинга 14.1)




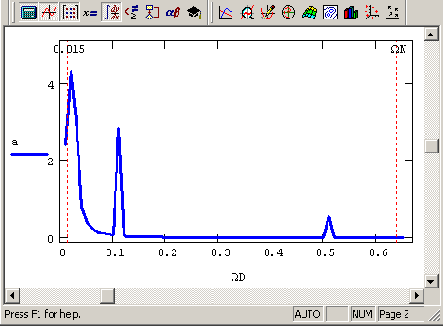
График спектра мощности данных модельной зависимости сигнал / шум (продолжение листинга 14 3)



Рисунок 14.13. График спектра мощности данных модельной зависимости сигнал / шум (продолжение листинга 14.3)


 




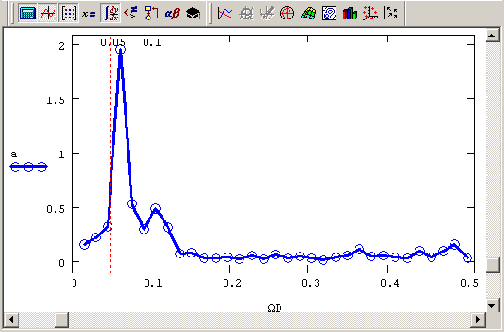
Иллюстрация влияния конечности выборки на расчет низкочастотной части Фурьеспектра



Рисунок 14.7. Иллюстрация влияния конечности выборки на расчет низкочастотной части Фурье-спектра



Сдвиг ноль-линии

Еще одним, наиболее ярким, проявлением вредного влияния конечности интервала выборки может служить расчет Фурье-преобразования суммы гармонического сигнала и константы (Рисунок 14.8). Для того чтобы получить данный рисунок, достаточно еще слегка (по сравнению с Рисунок 14.7) модифицировать строку листинга, касающуюся определения компонент вектора у, добавив к нему i: yi:=sin(2?0.915xi)+1.

Сравнивая Рисунок 14.7 и 14.8, несложно догадаться, почему так разительно изменился вид спектра в низкочастотной области. Пугающий рост спектра на левом крае частотного интервала объясняется совокупностью двух факторов: конечности выборки и добавлением к сигналу ненулевой постоянной составляющей (так называемым сдвигом ноль-линии). Сумма сигнала и константы определяет соответствующее влияние на вычисленный спектр, который также оказывается (просто в силу линейности операции интегрирования) суммой спектров сигнала и ступенчатой функцией (равной той самой константе внутри расчетного интервала и нулю за его пределами).



Исходные модельные данные (продолжение листинга 14 1)



Рисунок 14.1. Исходные модельные данные (продолжение листинга 14.1)



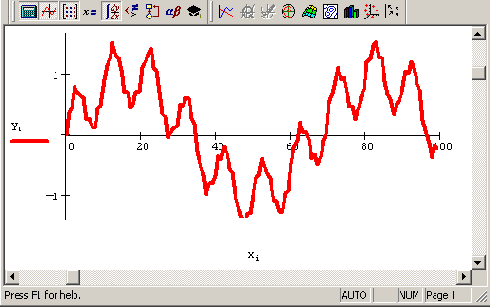
Чтобы смысл преобразования Фурье был более понятен, используем в качестве модельных данных дискретизацию детерминированного сигнала,, равного сумме трех синусоид (Рисунок 14.1).



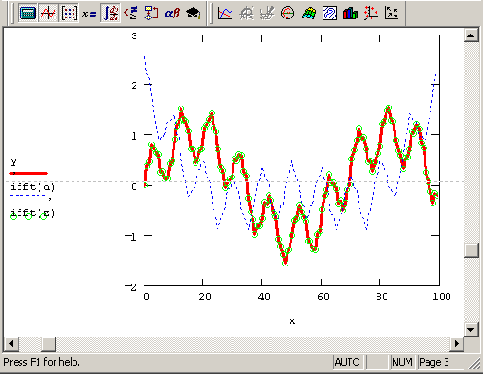
Исходный модельный сигнал (кружки)



Рисунок 14.24. Исходный модельный сигнал (кружки) и результат его фильтрации на основе Фурье-преобразования (продолжение листинга 14.11)





Комплексное преобразование Фурье (продолжение листинга 14 2)



Рисунок 14.6. Комплексное преобразование Фурье (продолжение листинга 14.2)


 




Быстрое преобразование Фурье



Листинг 14.1. Быстрое преобразование Фурье



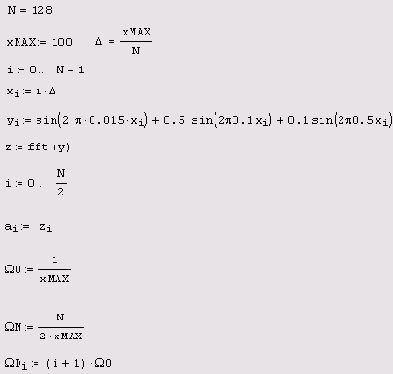
демонстрирует расчет



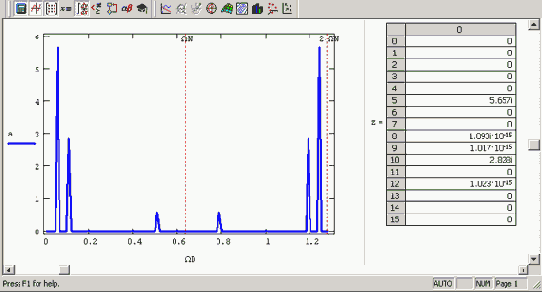
Листинг 14.1 демонстрирует расчет Фурье-спектра по N=128 точкам, причем предполагается, что интервал дискретизации данных yi равен ?. В середине листинга применяется встроенная функция fft, а его оставшаяся часть предназначена для корректного пересчета соответствующих значений частот ?i (они вычисляются в последней строке листинга). Обратите внимание, что результаты расчета представляются в виде модуля Фурье-спектра (Рисунок 14.2), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра (Рисунок 14.3) с определением синусоид в листинге 14.1.

Комплексное быстрое преобразование Фурье (продолжение листинга 14 1)



Листинг 14.2. Комплексное быстрое преобразование Фурье (продолжение листинга 14.1)



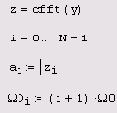
Расчет спектра мощности для модели сигнал/шум



Листинг 14.3. Расчет спектра мощности для модели сигнал/шум



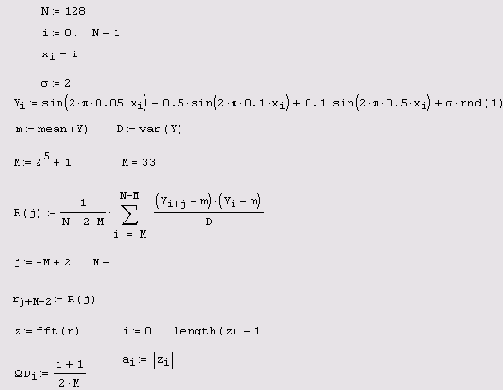
Двумерное преобразование Фурье



Листинг 14.4. Двумерное преобразование Фурье



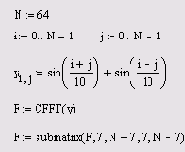
Поиск вейвлетспектра Добеши



Листинг 14.5. Поиск вейвлет-спектра Добеши



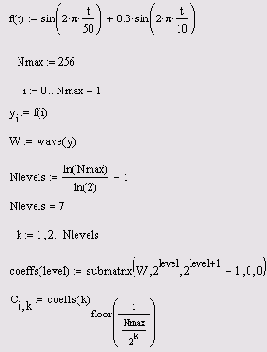
Поиск вейвлетспектра на основе "мексиканской шляпы"



Листинг 14.6. Поиск вейвлет-спектра на основе "мексиканской шляпы"


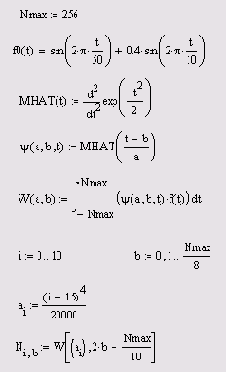
Примечание 1
Примечание 1

Программа листинга очень проста, но исключительно далека от хорошей в смысле быстродействия. Каждый интеграл вычисляется независимо, без использования методов ускорения, типа применяемых в алгоритме БПФ. Однако простые приемы программирования вполне доступно раскрывают математический смысл вейвлет-преобразования.



Сглаживание с последующей сплайнинтерполяцией



Листинг 14.7.  Сглаживание с последующей сплайн-интерполяцией



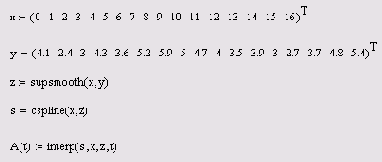
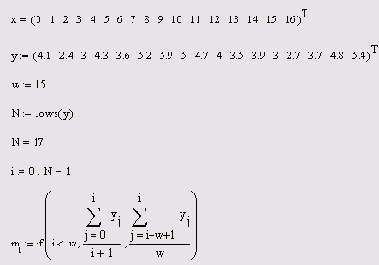
Сглаживание скользящим усреднением



Листинг 14.8. Сглаживание скользящим усреднением


Примечание 1
Примечание 1

Приведенная программная реализация скользящего усреднения самая простая, но не самая лучшая. Возможно, вы обратили внимание, что все кривые скользящего среднего на Рисунок 14.21 слегка "обгоняют" исходные данные. Почему так происходит, понятно: согласно алгоритму, заложенному в последнюю строку листинга 14.8, скользящее среднее для каждой точки вычисляется путем усреднения значений предыдущих w точек. Чтобы результат скользящего усреднения был более адекватным, лучше применить центрированный алгоритм расчета по w/2 предыдущим и w/2 последующим значениям. Он будет немного сложнее, поскольку придется учитывать недостаток точек не только в начале (как это сделано в программе с помощью функции условия if), но и в конце массива исходных данных.

 


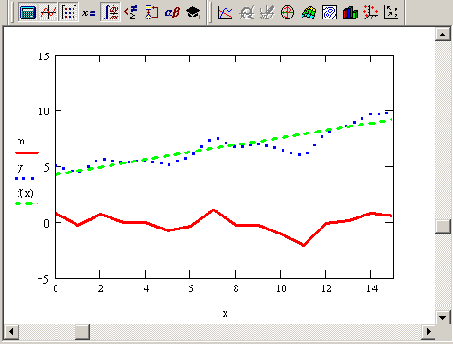
Устранение тренда



Листинг 14.9. Устранение тренда


На Рисунок 14.22 показаны исходные данные (кружками), выделенный с помощью регрессии линейный тренд (сплошной прямой линией) и результат устранения тренда (пунктир, соединяющий крестики).



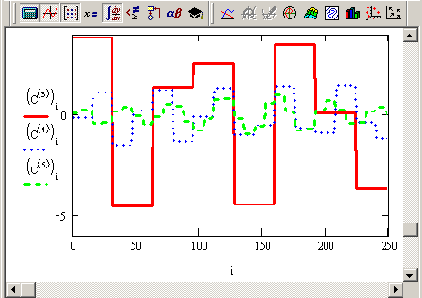
Полосовая фильтрация



Листинг 14.10. Полосовая фильтрация



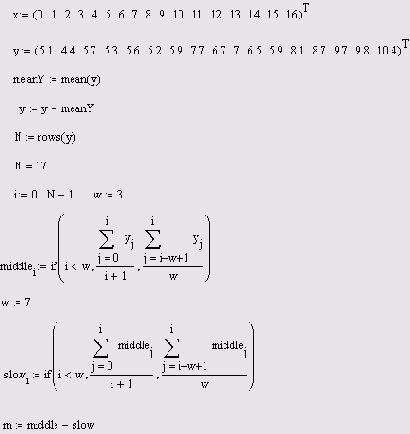
Фильтрация на основе преобразования Фурье



Листинг 14.11. Фильтрация на основе преобразования Фурье



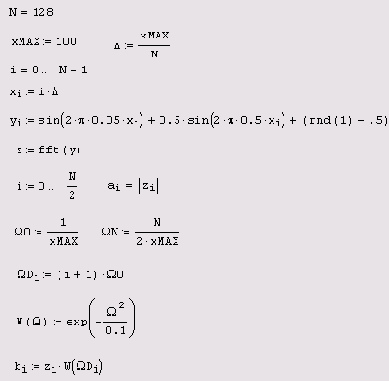
отличается от листинга



Листинг 14.11 отличается от листинга 14.1 (см. разд. 14.1. Г), главным образом, последними двумя строками, в которых, собственно, и определяется явный вид спектрального фильтра w(?), или, по-другому, спектральное окно. Обратное Фурье-преобразование спектра произведения спектрального окна w(?) и Фурье-спектра сигнала z, представляющее собой результат фильтрации, показано на Рисунок 14.24 сплошной кривой.

Вычисление спектра мощности



Листинг 14.12. Вычисление спектра мощности



Матрицарезультат вычисления Фурьеспектра данных (продолжение листинга 14 1)



Рисунок 14.2. Матрица-результат вычисления Фурье-спектра данных (продолжение листинга 14.1)



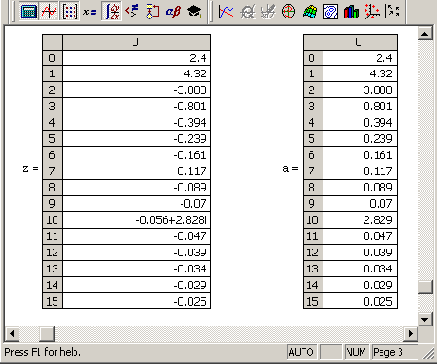
Исключительно важными представляются два параметра, заданные в предпоследней строке листинга 14.1, называемые соответственно граничной частотой и частотой Найквиста. Граничная частота ?0 определяет нижнюю, а частота Найквиста ?N — верхнюю границу аргумента вычисленного спектра, как показано маркерами на Рисунок 14.3. Кроме того, важно, что интервал дискретизации Фурье-спектра также равен ?0, а общее число вычисляемых точек спектра составляет N/2 (в нашем примере N/2=64). Последние утверждения иллюстрируются маркерами на Рисунок 14.4, изображающем график Фурье-спектра вблизи нижней границы частот.



Модель сигнал / шум



Рисунок 14.10. Модель сигнал / шум




Низкочастотная область Фурьеспектра (продолжение листинга 14 1)



Рисунок 14.4. Низкочастотная область Фурье-спектра (продолжение листинга 14.1)


 




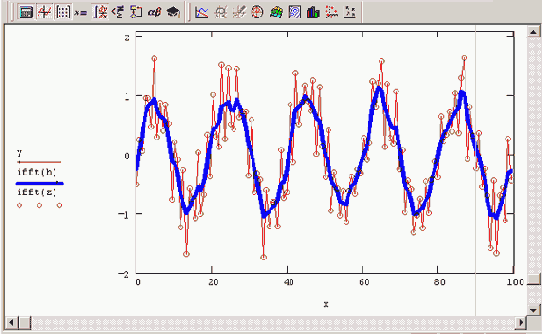
Обратное преобразование Фурье (продолжение листинга 14 1)



Рисунок 14.5. Обратное преобразование Фурье (продолжение листинга 14.1)



Видно, что в рассматриваемом случае сигнал у(х) восстановлен с большой точностью, что характерно для плавного изменения сигнала. Если же в качестве аргумента функции ifft использовать модуль Фурье-спектра (мы присвоили этому вектору в листинге 14.1 имя а), то профиль исходного сигнала будет реконструирован правильно, но окажется сдвинутым на определенное расстояние вдоль оси х. Так происходит из-за того, что взятие абсолютной величины комплексного спектра уничтожает информацию об относительной фазе отсчетов данных.

 


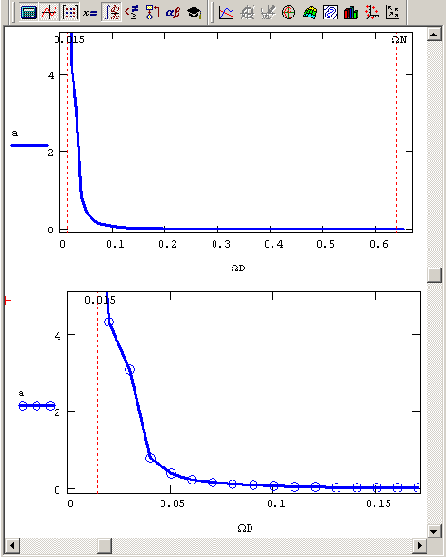
Расчеты Фурьеспектров гармонических сигналов с разной частотой ("маскировка частот")



Рисунок 14.9. Расчеты Фурье-спектров гармонических сигналов с разной частотой ("маскировка частот")



Избавиться от искажений, вызванных сдвигом ноль-линии, довольно просто. Достаточно (до Фурье-преобразования) вычислить среднее значение выборки и затем вычесть его из каждого элемента выборки. Если после этой операции вычислить Фурье-спектр, то он окажется примерно таким, как показано на Рисунок 14.7.

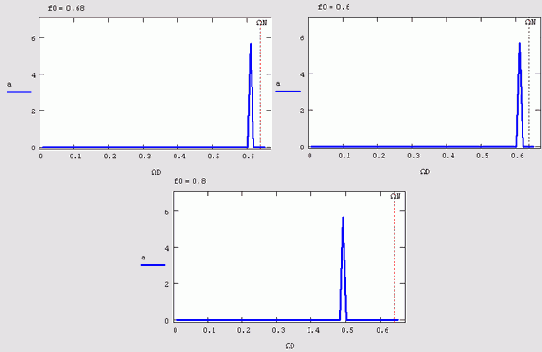
Маскировка частот

Еще один классический пример ошибочного расчета Фурье-спектра связан с возможным присутствием в сигнале гармоник с частотой, превышающей частоту Найквиста, в данном примере ?N=0.б4 (см. разд. 14.1.Г). Иллюстрация эффекта, называемого "маскировкой частот", приведена на Рисунок 14.9, который содержит расчет спектров трех различных синусоидальных сигналов с разной частотой f0. Первый спектр сигнала с частотой, меньшей частоты Найквиста, вычислен верно, а вот два остальных спектра показывают, что в случае превышения частоты Найквиста в спектре начинают присутствовать "лишние" пики. Появление артефактов спектра связано с тем, что дискретных отсчетов начинает не хватать для того, чтобы прописать высокочастотные гармоники с достаточной информативностью.

Примечание 3
Примечание 3

Напоминаем, что все листинги, имеющиеся в книге, а также документы Mathcad с расчетами всех рисунков, вы найдете на прилагаемом компакт-диске.

 


Результат полосовой фильтрации (продолжение листинга 14 10)



Рисунок 14.23. Результат полосовой фильтрации (продолжение листинга 14.10)


 




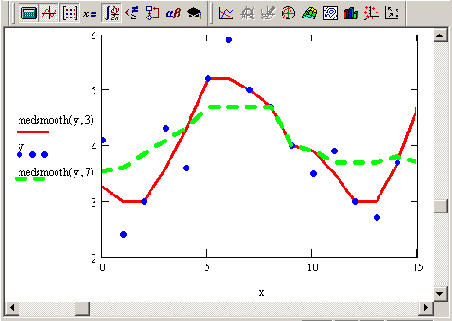
Сглаживание "бегущими медианами"



Рисунок 14.19. Сглаживание "бегущими медианами"




Сглаживание и фильтрация



14.3. Сглаживание и фильтрация



При анализе данных часто возникает задача их фильтрации, заключающаяся в устранении одной из составляющих зависимости y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые чаще всего обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая. В связи с этим считают, что сглаживание является частным случаем более общей задачи фильтрации сигнала, которая связана с подавлением определенных диапазонов частот спектра.

Наиболее простым и эффективным рецептом сглаживания (smoothing) можно считать регрессию различного вида, разобранную в предыдущей главе (см. разд. 13.2). Однако регрессия часто уничтожает информативную составляющую данных, оставляя лишь наперед заданную пользователем зависимость.

Часто рассматривают противоположную задачу фильтрации — устранение медленно меняющихся вариаций в целях исследования высокочастотной составляющей. В этом случае говорят о задаче устранения тренда. Иногда интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением полосовой фильтрации.

Несколько примеров программной реализации различных вариантов фильтрации приведены в данном разделе.

 




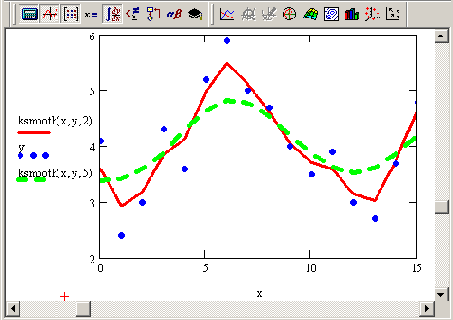
Сглаживание при помощи функции ksmooth



Рисунок 14.20. Сглаживание при помощи функции ksmooth


 




Скользящее усреднение с разными w=3 5 15 (листинг 14 8 коллаж трех графиков)



Рисунок 14.21. Скользящее усреднение с разными w=3, 5,15 (листинг 14.8, коллаж трех графиков)



Чтобы реализовать в Mathcad скользящее усреднение, достаточно очень простой программы, приведенной в листинге 14.8. Она использует только значения у, оформленные в виде вектора, неявно предполагая, что они соответствуют значениям аргумента х, расположенным через одинаковые промежутки. Вектор х применялся лишь для построения графика результата (Рисунок 14.21).



Спектральный анализ



Спектральный анализ



Мощным инструментом обработки данных, определенных дискретной зависимостью y(xi) или непрерывной функцией f(x) (полученной, например посредством интерполяции или регрессии, как об этом рассказано в главе 13), является спектральный анализ, имеющий в своей основе различные интегральные преобразования. Спектральный анализ используется как в целях подавления шума, так и для решения других проблем обработки данных. Спектром совокупности данных у(х) называют некоторую функцию другой координаты (или координат) F(w), полученную в соответствии с определенным алгоритмом. Примерами спектров являются преобразование Фурье (см. разд. 14. Т) и вейвлет-преобразование (си. разд. 14.2). Напомним, что некоторые преобразования, например, Фурье и Лапласа, можно осуществить в режиме символьных вычислений (см. главу 5). Каждое из интегральных преобразований эффективно для решения своего круга задач анализа данных.

Задачами, непосредственно связанными со спектральным анализом, являются проблемы сглаживания и фильтрации данных (см. разд. 14.3). Они заключаются в построении для исходной экспериментальной зависимости y(xi) некоторой (непрерывной или дискретной) зависимости f (х), которая должна приближать ее, учитывая к тому же, что данные (xi,yi) получены с некоторой погрешностью, выражающей шумовую компоненту измерений. При этом функция f (х) с помощью того или иного алгоритма уменьшает погрешность, присутствующую в данных (xi,yi). Такого типа задачи называют задачами фильтрации. Сглаживание путем построения регрессии данных (см. разд. 13.2) — это частный случай фильтрации.

Примечание 1
Примечание 1

Здесь нельзя не отметить, что в качестве дополнений к Mathcad поставляются три пакета расширения, включающие большое количество дополнительных встроенных функций для обработки данных. Названия пакетов расширения говорят сами за себя: Wavelet extension pack (Вейвлет-анализ данных), Signal processing (Анализ сигналов) и Image processing (Анализ изображений). Работа с пакетами расширения не слишком отличается от обычных приемов работы с Mathcad — следует только установить их определенным образом, как описано в руководстве пользователя Mathcad. Рассмотрение их возможностей выходит далеко за пределы данной книги, поэтому лишь упомянем о том, что описание встроенных функций и примеры их применения рассмотрены в трех электронных книгах, представляющих, соответственно, три упомянутых пакета расширения. Получить доступ к нужной книге можно, наводя указатель мыши на пункт E-Books (Электронные книги) в меню Help (Справка) и выбирая в открывающемся подменю имя нужного пакета расширения.

 


Сравнение синусоиды и вейвлетобразующей функции



Рисунок 14.15. Сравнение синусоиды и вейвлетобразующей функции



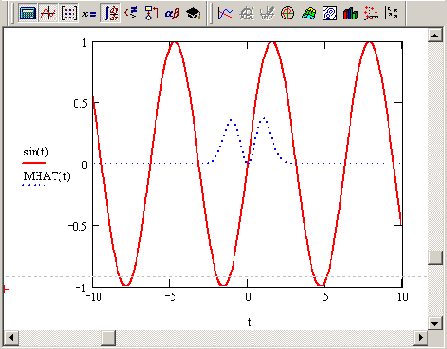
Из-за своего математического смысла вейвлет-спектр имеет не один аргумент, а два. Помимо частоты, вторым аргументом ь является место локализации вейвлетобразующей функции. Поэтому b имеет ту же размерность, что и х.

 


Устранение тренда (продолжение листинга 14 9)



Рисунок 14.22. Устранение тренда (продолжение листинга 14.9)


 




Вейвлетспектр на основе функции Добеши (продолжение листинга 14 5)



Рисунок 14.16. Вейвлет-спектр на основе функции Добеши (продолжение листинга 14.5)


 




Вейвлетспектр на основе "мексиканской шляпы" (продолжение листинга 14 6)



Рисунок 14.17. Вейвлет-спектр на основе "мексиканской шляпы" (продолжение листинга 14.6)


 




Вейвлетспектры



14.2. Вейвлет-спектры



В последнее время возрос интерес к другим интегральным преобразованиям, в частности, вейвлет-преобразованию (или дискретному волновому). Оно применяется, главным образом, для анализа нестационарных сигналов и для многих задач подобного рода оказывается более эффективным, чем преобразование Фурье. Основным отличием вейвлет-преобразования является разложение данных не по синусоидам (как для преобразования Фурье), а по другим функциям, называемым вейвлетобразующими. Вейвлетобразующие функции, в противоположность бесконечно осциллирующим синусоидам, локализованы в некоторой ограниченной области своего аргумента, а вдали от нее равны нулю или ничтожно малы. Пример такой функции, называемой "мексиканской шляпой", показан на Рисунок 14.15.



П 2 4 Панель Graph (График)



Таблица П.2.4. Панель Graph (График)


Оператор
 Перевод
 Горячие клавиши
X-Y Plot
 X-Y (декартовый) график
 <Shift>+<2>
Zoom
 Масштаб графика
 &nbsp
Trace
 Трассировка графика
 &nbsp
Polar Plot
 Полярный график
 <Ctrl>+<7>
Surface Plot
 График трехмерной поверхности
 <Ctrl>+<2>
Contour Plot
 График линий уровня
 <Ctrl>+<5>
3D Bar Plot
 Трехмерная гистограмма
 &nbsp
Vector Field Plot
 Векторное поле
 &nbsp
3D Scatter Plot
 Трехмерное множество точек
 &nbsp

 


П2 1 Команды меню



Таблица П2.1. Команды меню


Меню
 Команда
 Перевод
Горячие клавиши
 Описание
File

(Файл)
&nbsp &nbsp 		New
 Создать
 <Ctrl>+<N>
 Создать новый документ
Open
 Открыть
 <Ctrl>+<0>
 Открыть существующий документ
Close
 Закрыть
 <Ctrl>+<W>
 Закрыть активный документ
Save
 Сохранить
 <Ctrl>+<S>
 Сохранить активный документ
Save As
 Сохранить как
 &nbsp Сохранить активный документ в другом файле
Save As Web Page
 Сохранить как Web-страницу
 &nbsp Сохранить копию активного документа в файле формата HTML
Page Setup
 Параметры страницы
 &nbsp Опции вывода активного документа на печать
Print Preview
 Просмотр
 &nbsp Предварительный просмотр на экране вывода на печать активного документа
Print
 Печать
 <Ctrl>+<P>
 Распечатать активный документ
Send
 Отправить
 &nbsp Отправить активный документ по электронной почте
Properties
 Свойства
 &nbsp Свойства документа (примечания, опции XML и т. п)
Exit
 Выход
 &nbsp Завершение работы с Mathcad
Edit

(Правка)
&nbsp
&nbsp 		Undo
 Отменить
 <Ctrl>+<Z>
 Отменить последнее действие
Redo
 Повторить
 <Ctrl>+<Y>
 Повторить последнее отмененное действие
Cut
 Вырезать
 <Ctrl>+<X>
 Вырезать выбранное выражение в буфер
Copy
 Копировать
 <Ctrl>+<C>
 Копировать выбранное выражение в буфер
Paste
 Вставить
 <Ctrl>+<V>
 Вставить выражение из буфера
Paste Special
 Специальная вставка
 &nbsp Вставить объект специального формата, находящийся в буфере
Delete
 Удалить
 <Ctrl>+<D>
 Удалить выбранный регион
Select All
 Выделить все
 <Ctrl>+<A>
 Выделить всю рабочую область
Find
 Найти
 <Ctrl>+<F>
 Поиск текста
Replace
 Заменить
 <Ctrl>+<H>
 Замена искомого текста другим
Go to Page
 Перейти к странице
 &nbsp Переход к другой странице
Links
 Ссылки
 &nbsp Управление связями OLE с другими приложениями
Object
 Объект
 Активизировать вставленный объект OLE
View

(Вид)
 Toolbars
 Панели инструментов
 Показать или скрыть панели инструментов
Ruler
 Линейка
 Показать или скрыть линейку
Status Bar
 Строка состояния
 Показать или скрыть строку состояния
Header and Footer
 Верхний и нижний колонтитулы
 Изменить колонтитулы для распечатываемых страниц
Regions
 Регионы
 Показать или скрыть границы регионов
Annotations
 Примечания
 Показать или скрыть примечания
Refresh
 Обновить
 <Ctrl>+<R> Обновить документ
Zoom
 Масштаб
 Изменить масштаб отображения документа
Insert

(Вставка)
&nbsp 		Graph
 График
 Вставить график (с выбором типа графика из подменю)
Matrix
 Матрица
 <Ctrl>+<M> Вставить матрицу или вектор
Function
 Функция
 <Ctrl>+<E> Вставить встроенную функцию
Unit
 Единицы
 <Ctrl>+<U> Вставить единицы измерения размерной величины
Picture
 Рисунок
 <Ctrl>+<T> Создать рисунок для отображения матрицы
Area
 Область
 Создать зону
Page Break
 Разрыв страницы
 Начать новую страницу
Math Region
 Математическая область
 <Ctrl>+ +<Shift>+<A>
 Создать математическую область в тексте
Text Region
 Текстовая область
 <">
 Создать текстовую область в документе
Component
 Компонент
 &nbsp Вставить компонент другого приложения
Data
 Данные
 &nbsp Вставить данные в различных форматах
Control
 Элемент управления
 &nbsp Вставить элемент управления
Object
 Объект
 &nbsp Внедрение объекта
Reference
 Ссылка
 &nbsp Вставить ссылку на другой документ
Hyperlink
 Гиперссылка
 <Ctrl>+<K>
 Вставить гиперссылку
Format

(Формат)
 Equation
 Формула
 &nbsp Форматирование формул
Result
 Результат
 &nbsp Форматирование вывода результатов вычислений
Text
 Текст
 &nbsp Форматирование текста
Paragraph
 Абзац
 &nbsp Изменение разметки абзаца
Tabs
 Табуляции
 &nbsp Установить табуляцию для документа или выделенного участка текста
Style
 Стиль текста
 &nbsp Определить или применить стиль — комбинацию настроек текстового формата
Properties
 Свойства
 &nbsp Изменение свойств области
Graph
 График
 &nbsp Изменения в графиках
Color
 Цвет
 &nbsp Настройка цвета
Area
 Область
 &nbsp Работа с зоной
Separate Regions
 Разделить регионы
 &nbsp Разделить перекрывающиеся регионы в документе
Align Regions
 Выровнять регионы
 &nbsp Выравнивание региона по горизонтали или вертикали
Repaginate Now
 Разбить на страницы
 &nbsp Разбиение документа на страницы
Tools

(Сервис)
 Spelling
 Проверка орфографии
 &nbsp Проверка орфографии текстовых регионов
Animation
 Анимация
 &nbsp Создать или воспроизвести анимацию
Protect Worksheet
 Запереть документ
 &nbsp Защита документа от редактирования
Calculate
 Пересчитать
 <F9>
 Управление вычислением формул
Optimize
 Оптимизировать
 &nbsp Управление режимом оптимизации расчетов
Disable Evabion
 Отключить вычисления
 &nbsp Вкл. / Выкл. вычисления формулы
Trace Error
 Трассировка ошибки
 &nbsp Трассировка источника сообщения об ошибке
Worksheet Options
 Опции документа
 &nbsp Установка опций математики
License
 Лицензия
 &nbsp Параметры лицензирования копии Mathcad
Preferences
 Настройки
 &nbsp Изменить основные настройки
Symbolics

(Символика)
 Evaluate
 Вычислить
 &nbsp Вычислить выражение в виде числа, если это возможно
Simplify
 Упростить
 &nbsp Упростить выражение
Expand
 Разложить
 &nbsp Представить выражение в более развернутом виде
Factor
 Разложить на множители
 &nbsp Разложить полином или целое число на простые множители
Collect
 Привести подобные
 &nbsp Привести подобные слагаемые
Polynomial Coefficients
 Коэффициенты полинома
 &nbsp Вычислить полиномиальные коэффициенты
Variable
 Переменная
 &nbsp Символьные действия с выделенной переменной
Matrix
 Матрица
 &nbsp Символьные действия с матрицей
Transform
 Преобразование
 &nbsp Символьные интегральные преобразования
Evaluation Style
 Стиль вычислений
 &nbsp Изменить показ символьных ответов
Window

(Окно)
 Cascade
 Каскад
 &nbsp Расположить окна документов каскадом
&nbsp Tile Horizontal
 По горизонтали
 &nbsp Расположить окна документов по горизонтали
&nbsp Tile Vertical
 По вертикали
 &nbsp Расположить окна документов по вертикали
&nbsp *
 (Имя документа)
 &nbsp Активизировать окно*
Help

(Справка)
&nbsp 		MathcadHelp
 Справка
 <F1>
 Получение справочной информации
What's This?
 Что это такое?
 &nbsp Быстрая интерактивная справка об элементах интерфейса
Developer's Reference
 Справка для разработчиков
 &nbsp Дополнительная справка для разработчиков
Author's Reference
 Справка для авторов
 &nbsp Дополнительная справка для авторов электронных книг
Tutorials
 Учебники
 &nbsp Доступ к электронным книгам учебников
QuickSheets
 Быстрые шпаргалки
 &nbsp Доступ к электронным книгам Быстрых шпаргалок
Reference Tables
 Справочный стол
 &nbsp Доступ к электронной книге со справочными таблицами
E-Books
 Электронные книги
 &nbsp Открыть существующую в виде файла электронную книгу или пакет расширения
User's Forum
 Форум
 &nbsp Перейти на форум пользователей Mathcad
Mathcad.com
 Mathcad.com
 &nbsp Перейти на сайт Mathcad
Mathcad Update
 Обновление Mathcad
 &nbsp Проверить сайт компании MathSoft на наличие обновлений версии Mathcad 12
About Mathcad
 О программе
 &nbsp Информация о текущей версии Mathcad
Register Mathcad
 Регистрация
 &nbsp Онлайн-регистрация копии Mathcad

 


П2 2 Панель Math (Математика)



Таблица П2.2. Панель Math (Математика)


Панель
 Перевод
Calculator Toolbar
 Калькулятор
Graph Toolbar
 График
Matrix Toolbar
 Матрица
Evaluation
 Выражения
Calculus
 Вычисления
Boolean
 Булевы операторы
Programming
 Программирование
Greek Symbols Toolbar
 Греческие символы
Symbolic Keyword Toolbar
 Символика
 




П2 3 Панель Calculator (Калькулятор)



Таблица П2.3. Панель Calculator (Калькулятор)


Оператор
 Перевод
 Горячие клавиши
Sin
 Синус
 &nbsp
Cos
 Косинус
 &nbsp
Tan
 Тангенс
 &nbsp
Ln
 Натуральный логарифм
 &nbsp
Log
 Десятичный логарифм
 &nbsp
n!
 Факториал
 <!>
1
 Ввод мнимой единицы
 <1>, <i>
|x|
 Модуль
 <Shift>+<\>
v
 Квадратный корень
 <\>
vn
 Корень n-й степени
 <Ctrl>+<\>
ex
 Экспонента
 &nbsp
1/x
 Обратная величина
 &nbsp
()
 Скобки
 <'>
x2
 Возведение в квадрат
 &nbsp
xy
 Возведение в степень у
 <^>
?
 Ввод числа n
 <Ctrl>+<Shift>+<P>
/
 Деление
 </>
./
 Смешанное число
 <Ctrl>+<Shift>+<+>
X
 Умножение
 <*>
+
 Деление в одну строку
 <Ctrl>+</>
+
 ' Сложение
 <+>
:=
 Присваивание
 <:>
.
 Десятичная точка
 <.>
0,1,2 ..... 9
 Числа 0...9
 <0>,<1>, <2> ..... <9>
—
 Вычитание ("минус")
 <->
:=
 Вычислить численно ("равно")
 <=>

 


П2 5 Панель Matrix (Матрица)



Таблица П2.5. Панель Matrix (Матрица)


Оператор
 Перевод
 Горячие клавиши
Matrix or Vector
 Матрица или вектор
 <Ctrl>+<M>
Subscript
 Нижний индекс
 <[>
Inverse
 Обратная матрица
 &nbsp
Determinant
 Определитель
 <|><Shift>+<\>
Vectorize
 Векторизовать
 <Ctrl>+<->
Matrix Column
 Выделение столбца
 <Ctrl>+<6>
Matrix Transpose
 Транспонирование
 <Ctrl>+<1>
Range Variable
 Ранжированная переменная
 <;>
Cross Product
 Векторное произведение
 <Ctrl>+<8>
Dot Product
 Умножение
 <*>
Vector Sum
 Сумма вектора
 <Ctrl>+<4>
Picture
 Рисунок
 <Ctrl>+<T>

 


П2 6 Панель Evaluation (Выражения)



Таблица П2.6. Панель Evaluation (Выражения)


Оператор
 Перевод
 Горячие клавиши
Evaluate Numerically =
 Вычислить численно ("равно")
 <=>
Definition :=
 Присваивание
 <:>
Global Definition я
 Глобальное присваивание
 <~>
Evaluate Symbolically ->
 Вычислить символьно
 <Ctrl>+<.>
Symbolic Keyword Evaluation ->
 Символьное вычисление с ключевым словом
 <Ctrl>+<Shift>+<.>
Prefix Operator fx
 Оператор "перед"
 &nbsp
Postfix Operator xf
 Оператор "после"
 &nbsp
Infix Operator xfy
 Оператор "внутри"
 &nbsp
Tree Operator xfy
 Оператор "дерево"
 &nbsp

 


П2 7 Панель Calculus (Вычисления)



Таблица П2.7. Панель Calculus (Вычисления)


Оператор
 Перевод
 Горячие клавиши
Derivative
 Производная
 <?>
Nth Derivative
 Л/-я производная
 <Ctrl>+<?>
Infinity o°
 Символ бесконечности
 <Ctrl>+<Shift>+<2>
Definite Integral
 Определенный интеграл
 <&>
Summation
 Сумма
 <Ctrl>+<Shift >+<4>
Iterated product
 Произведение
 <Ctrl>+<Shift >+<3>
Indefinite Integral
 Неопределенный интеграл
 <Ctrl>+<!>
Summation with range variables
 Сумма ранжированной переменной
 <Ctrl>+<4>
Iterated product with range variables
 Произведение ранжированной переменной
 <Ctrl>+<3>
Two-sided limit
 Предел
 <Ctrl>+<L>
Left-sided limit
 Левый предел
 <Ctrl>+<A>
Right-sided limit
 Правый предел
 <Ctrl>+<B>

 


П2 8 Панель Boolean (Булевы операторы)



Таблица П2.8. Панель Boolean (Булевы операторы)


Оператор
 Перевод
 Горячие клавиши
Equal =
 Равно
 <Ctrl>+<=>
Less than <
 Меньше
 «>
Greater than >
 Больше
 <»
Less than or equal <
 Меньше или равно
 <Ctrl>+<9>
Greater than or equal >
 Больше или равно
 <Ctrl>+<0>
Not equal to
Не равно
 <Ctrl>+<3>
Not
 Не
 <Ctrl>+<Shift>+<1>
And
И
 <Ctrl>+<Shift>+<7>
Or v
 ИЛИ
 <Ctrl>+<Shift>+<6>
Exclusive or
Исключающее ИЛИ
 <Ctrl>+<Shift>+<5>

 


П2 9 Панель Controls (Элементы управления)



Таблица П2.9. Панель Controls (Элементы управления)


Оператор
 Перевод
Check Box
 Флажок проверки
Radio Button
 Переключатель
Push Button
 Кнопка
Slider
 Ползунковый регулятор
Text Box
 Поле текстового ввода
List Box
 Список

 


П 3 3 Встроенные функции



Таблица П.3.3. Встроенные функции


Функция
 Аргументы
 Описание
a*(z)
 z — аргумент
 Обратная тригонометрическая или гиперболическая функция *
Ai(x)
 x — аргумент
 Функция Эйри первого рода
angle (x,y)
 x, у — коорднинаты точки
 Угол между точкой и осью ох
APPENDPRN (file)
 file — строковое представление пути к файлу
 Дозапись данных в существующий текстовый файл
arg(z)
 z — аргумент функции
 Аргумент комплексного числа
atan2 (x, y)
 х, у — коорднинаты точки
 Угол, отсчитываемый от оси ох

ДО ТОЧКИ (х,у)
augment (A,B,C, ...)
 А, в, с, ... — векторы или матрицы
 Слияние матриц слева направо
bei (n, x) ber (n, x)
 n — порядок х — аргумент
 Мнимая и действительная части функции Бесселя— Кельвина
Bi(x)
 х — аргумент
 Функция Эйри второго рода
bspline (x, у, и, n)
 x, у — векторы данных

u — вектор значений сшивок В-сплайнов

n — порядок полиномов
 Вектор коэффициентов В-сплайна
Bulstoer (y0,t0,tl,M,D)
 См. rkfixed
 Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша— Штера
bulstoer (y0,t0,t1, ace, D, k, s)
 См. rkadapt
 Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала)
bvalfit (z1,z2, x0,

xl,xf , D, loadl, Ioad2, score)
 zl, z2 — вектор начальных значений для недостающих левых и правых граничных условий

х0 — левая граница xl — правая граница xf — внутренняя точка

D (х, у) — векторная функция, задающая систему ОДУ

loadl (x0, z) , load2 (x1, z) — векторные функции, задающие левые и правые граничные условия

score (xf, у) —векторная функция, задающая сшивку решений в xf
 Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке
ceil (x)
 х — аргумент
 Наименьшее целое, не меньшее х
cfft (y), CFFT(y)
 у — вектор данных
 Вектор прямого комплексного преобразования Фурье (в разных нормировках)
cholesky (A)
 А — квадратная, определенная матрица
 Разложение Холецкого
cols (A)
 А — матрица или вектор
 Число столбцов
concat (S1,S2, . .-)
 s1, s2, . . . —строки
 Объединение строковых переменных
condl(A), cond2 (A) , conde (A) , condi (A)
 A — квадратная матрица
 Числа обусловленности в разных нормах (L1, L2, евклидова, °°)
cos (z)
 z — аргумент
 Косинус
cosh (z)
 z — аргумент
 Гиперболический косинус
cot (z)
 z — аргумент
 Котангенс
coth(z)
 z — аргумент
 Гиперболический котангенс
csort (A, i)
 A — матрица i — индекс столбца
 Сортировка строк матрицы по элементам 1-го столбца
CreateMeshfF, s 0,sl,

t0, tl, sgr, tgr, fmap)
 F ( s , t ) — векторная функция из трех элементов

to,tl — пределы t s0,s1 — пределы s

tgr, sgr — число точек сетки по t и s

fmap — функция преобразования координат
 Создание вложенного массива, представляющего х-, у- и z-координаты параметрической поверхности, заданной функцией F
CreateSpace (F[,t0,t1, tgr, fmap] )
 F ( t ) — векторная функция из трех элементов

t0,t1 — пределы t

tgr — число точек сетки

по t

fmap — функция преобразования координат
 Создание вложенного массива, представляющего х-, у- и z-координаты параметрической пространственной кривой, заданной функцией F
csc(z)
 z — аргумент
 Косеканс
csch (z)
 z — аргумент
 Гиперболический косеканс
csgn (z)
 z — аргумент
 Комплексный знак числа
cspline (x, y)
 х, у — векторы данных
 Вектор коэффициентов кубического сплайна
cy!2xyz(r,9,z)
 r , 6, z — цилиндрические координаты
 Преобразование цилиндрических координат в прямоугольные
D* (x,par)
 x — значение случайной величины

par — список параметров распределения*
 Плотность вероятности со статистикой распределения*
diag(v)
 v — вектор
 Диагональная матрица, на диагонали которой находятся элементы вектора
eigenvals (A)
 А — квадратная матрица
 Собственные значения матрицы
eigenvec (A,K)
 А — квадратная матрица А — собственное значение
 Собственный вектор матрицы, соответствующий заданному собственному значению
eigenvecs (A)
 А — квадратная матрица
 Собственные векторы матрицы
erf (x)
 х — аргумент
 Функция ошибок
erfc(x)
 х — аргумент
 Обратная функция ошибок
error (S)
 s — строка
 Возвращает строку s как сообщение об ошибке
exp(z)
 z — аргумент
 Экспонента в степени z
expfit (x,y,g)
 х, у — векторы данных

g — вектор начальных значений а, b, с
 Регрессия экспонентой аеbх+с
fft(y), FFT (y)
 у — вектор данных
 Вектор прямого преобразования Фурье (в разных нормировках)
fhyper (a,b,c,x)
 а, ь, с — параметры х — аргумент, -1<х<1
 Гауссова гипергеометрическая функция
Find (x1,x2, ...)
 x1 , х2 , . . . — переменные
 Возвращает корень алгебраического уравнения (скаляр) или системы (вектор), определенных в блоке с ключевым словом

Given
floor (x)
 х — аргумент
 Наибольшее целое число, меньшее или равное х
Gamma ( x ) , Gamma ( a , x )
 x — аргумент
 Гамма-функция Эйлера или неполная гамма-функция порядка а
genfit (x,y,g,G)
 x, у — векторы данных

g — вектор начальных значений параметров регрессии

G (х, с) — векторная функция, составленная из функции пользователя и ее частных производных по каждому параметру
 Вектор коэффициентов регрессии функциями пользователя общего вида
geninv (A)
 А — матрица
 Создание обратной матрицы
genvals (A, B)
 А, в — квадратные матрицы
 Расчет обобщенных собственных значений
genvecs (A, B)
 А, в — квадратные матрицы
 Расчет обобщенных собственных векторов
Given
 &nbsp Ключевое слово для ввода систем уравнений, неравенств и т. п.
heaviside step(x)
 х — аргумент
 Функция Хевисайда
Her (n,x)
 х — аргумент n — порядок
 Полином Эрмита
I0(x), I1(x), In (m,x)
 х — аргумент
 Модифицированная функция Бесселя первого рода нулевого, первого и т-го порядка
ibeta (a, x, y)
 х , у — аргументы а — параметр
 Неполная бета-функция
identity(N)
 N — размер матрицы
 Создание единичной матрицы
icfft(v), ICFFT(v)
 v — вектор частотных данных Фурье-спектра
 Вектор комплексного обратного преобразования Фурье (в разных нормировках)
if (cond,x,y)
 cond — логическое условие

х, у — значения, возвращаемые, если условие верно (ложно)
 Функция условия
if ft (v), IFFT(v)
 v — вектор частотных данных Фурье-спектра
 Вектор обратного преобразования Фурье (в разных нормировках)
isNaN(x)
 x — аргумент
 Возвращает 1, если x=NaN нов остальных случаях
IsString (x)
 х — аргумент
 Возвращает 1, если х — строка, и 0 в остальных случаях
iwave (v)
 v — вектор частотных данных вейвлет-спектра
 Вектор обратного вейвлет-преобразования
Im(z)
 z — аргумент
 Мнимая часть комплексного числа
interp (s,x,y,t)
 s — вектор вторых производных

х, у — векторы данных t — аргумент
 Сплайн-интерполяция
intercept (x,y)
 х, у — векторы данных
 Коэффициент b линейной регрессии b+ах
J0(x), Jl(x), Jn (m,x)
 х — аргумент
 Функция Бесселя первого рода нулевого, первого и m-го порядка
Jac (n, a, b,x)
 х — аргумент а , b — параметры n — порядок
 Полином Якоби
js (n,x)
 n — порядок х — аргумент
 Сферическая функция Бесселя первого рода
K0(x), Kl(x), Kn (m, x)
 х — аргумент
 Модифицированная функция Бесселя второго рода нулевого, первого и m-ro порядка
Kronecker delta (x, y)
 х , у — аргументы
 Дельта-символ Кронекера
ksmooth(x,y,b)
 х, у — векторы данных

b — ширина окна сглаживания
 Сглаживание с помощью функции Гаусса
Lag(n,x)
 x — аргумент n — порядок
 Полином Лагерра
last (v)
 v — вектор
 Индекс последнего элемента вектора
Leg(n,x)
 x — аргумент n — порядок
 Полином Лежандра
length (v)
 v — вектор
 Число элементов вектора
line(x,y)
 х, у — векторы данных
 Вектор из коэффициентов линейной регрессии b+ах
Unfit (x, y, F)
 х, у — векторы данных

F (х) — векторная функция пользователя
 Вектор коэффициентов регрессии функцией пользователя
linterp(x,y, t)
 х, у — векторы данных t — аргумент
 Кусочно-линейная интерполяция
Igsfit (x,y,g)
 х, у — векторы данных

g — вектор начальных значений а, Ь, с
 Регрессия логистической функцией а/(1+Ь-е~сх)
ln(z)
 z — аргумент
 Натуральный логарифм
Infit (x, y)
 х, у — векторы данных
 Регрессия логарифмической функцией a-ln(x)+b
loess (x, y, span )
 х, у — векторы данных

span — параметр размера полиномов
 Вектор коэффициентов для регрессии отрезками полиномов (применяется вместе с interp)
log(z)
 z — аргумент
 Десятичный логарифм
log(z, b)
 z — аргумент
 Логарифм z по основанию b
logfit (x, y, g)
 х, у — векторы данных

g — вектор начальных значений а, Ь, с
 Регрессия логарифмической функцией аln (х+b) +с
logpts (min,de c,N)
 min — показатель начала интервала,

dec — количество декад

N — число точек в пределах каждой декады
 Возвращает вектор из чисел, расположенных линейно-равномерно в пределах каждой логарифмической декады
Logspace (min,max,N)
 min,max — границы интервала

N — число точек
 Возвращает вектор из чисел, расположенных равномерно (в логарифмическом масштабе) на интервале (min,max)
Isolve (A,b)
 А — матрица СЛАУ b — вектор правых частей
 Решение системы линейных уравнений (СЛАУ)
Ispline (x, y)
 х, у — векторы данных
 Вектор коэффициентов линейного сплайна
lu(A)
 А — квадратная матрица
 LU-разложение
matrix (M,N,f )
 м — количество строк N — количество столбцов f ( i , j ) — функция
 Создание матрицы с элементами f (i, j)
Maximize (f , xl, . . . )
 f (xl, . . .) —функция

xl, . . . — аргументы, по которым производится максимизация
 Вектор значений аргументов, при которых функция f достигает максимума (возможно задание дополнительных условий в блоке с ключевым словом Given)
mhyper (a,b, x)
 х — аргумент а, Ь — параметры
 Конфлюэнтная гипергеометрическая функция
Minerr (Xl, x2, . ..)
 xi,x2, . . . — переменные
 Возвращает вектор приближенного решения системы уравнений и неравенств, определенных в блоке с ключевым словом

Given
Minimize (f ,xl, ...)
 f (xl, . . . ) —функция

xl, . . . — аргументы, по которым производится минимизация
 Вектор значений аргументов, при которых функция f достигает минимума (возможно задание дополнительных условий в блоке с ключевым словом Given)
medsmooth (y,b)
 у — вектор данных b — ширина окна сглаживания
 Сглаживание методом "бегущих медиан"
multigrid(F,nc ycle)
 F — матрица правой части уравнения Пуассона

ncycle — параметр алгоритма сеток
 Матрица решения уравнения Пуассона на квадратной области с нулевыми граничными условиями
n*(M,par)
 м — размерность вектора

x — значение случайной величины

par — список параметров распределения*
 Вектор случайных чисел со статистикой*
norml (A) , norm2 (A) , norme (A) , normi (A)
 А — квадратная матрица
 Нормы матриц (L1, L2, евклидова, )
num2str (z)
 2 — ЧИСЛО
 Возвращает строку, чьи знаки соответствуют десятичному значению числа z
Odesolve(t,tl[,s tep])
 t — переменная интегрирования ОДУ

tl — конечная точка интервала интегрирования

step — число шагов интегрирования ОДУ
 Возвращает матрицу с решением задачи Кош и для одного ОДУ, определенного в блоке с ключевым словом Given и начальными условиями в точке to
p* (x,par)
 х — значение случайной величины

par — список параметров распределения*
 Функция распределения со статистикой*
pdesolve (u, x, xrange, t, trang e, [xpts], [tpts]))
 и — вектор имен функций

х — пространственная переменная

xrange — интервал интегрирования по пространству

t — временная переменная

t range — интервал интегрирования по времени

xpts — число пространственных узлов сетки

tpts — число временных шагов сетки
 Возвращает скалярную функцию двух аргументов (х, t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных
роl2ху (r, 9)
 r , e — полярные координаты
 Преобразование полярных координат в прямоугольные
polyroots (v)
 v — вектор, составленный из коэффициентов полинома
 Возвращает вектор всех корней полинома
predict (y,m, n)
 у — исходный вектор

m — число элементов у, по которым строится экстраполяция

n — количество предсказываемых элементов
 Функция предсказания, экстраполирующая вектор .
pspline (x,y)
 х, у — векторы данных
 Вектор коэффициентов квадратичного сплайна
pwfit (x,y,g)
 х, у — векторы данных

g — вектор начальных значений а,b,с
 Регрессия степенной функцией

ахb+с
q* (p,par)
 р — значение вероятности

par — список параметров распределения*
 Квантиль (функция, обратная функции распределения) со статистикой*
qr(A)
 А — вектор или матрица
 QR-разложение
Radau(y0, t0, t 1, M,D)
 См. rkf ixed
 Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом RADAUS
radau(y0, t0, t 1, M,D)
 См. rkf ixed
 Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом RADAUS (для определения только последней точки интервала)
rank (A)
 А — матрица
 Ранг матрицы
Re(z)
 z — аргумент
 Действительная часть комплексного числа
READ* (file)
 file — строковое представление пути к файлу
 Запись данных в файл типа*
regress (x, y, k)
 х , у — векторы данных k — степень полинома
 Вектор коэффициентов для полиномиальной регрессии (применяется вместе с interp)
Relax (a,b,c,d,e,F, v,rjac)
 a, b, c, d, e — матрицы коэффициентов разностной схемы

F — матрица правой части уравнения

v — матрица граничных условий

г j ас — параметр алгоритма (0...1)
 Матрица решения методом сеток дифференциального уравнения в частных производных на квадратной области
reverse (v)
 v — вектор
 Перестановка элементов вектора в обратном порядке
Rkadapt (y0,t0, t1,

ace, D, k, s)
 у0 — вектор начальных условий

( t0 , t1) — интервал интегрирования

асе — погрешность вычисления

D ( t , у ) — векторная функция, задающая систему ОДУ

k — максимальное число шагов интегрирования

s — минимальный шаг интегрирования
 Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге— Кутты с переменным шагом и заданной точностью (для определения только последней точки интервала)
Rkadapt (y0,t0,t1,M,D)
 См. rkfixed
 Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге— Кутты с переменным шагом
rkfixed (yO,tO,tl,M,D)
 у0 — вектор начальных условий

{(1 0 , 1 1 ) — интервал интегрирования

M — число шагов интегрирования

D (t , у) — векторная функция, задающая систему ОДУ
 Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге— Купы с фиксированным шагом
root (f (x, . . .) ,x[a, b])
 f (x, . . . ) —функция x — переменная

( a , b ) — интервал поиска корня
 Возвращает корень функции
round (x, n)
 x — аргумент

n — число знаков округления после десятичной точки
 Округление
rows (A)
 А — матрица или вектор
 Число строк
rref(A)
 А — матрица или вектор
 Преобразование матрицы в ступенчатый вид
rsort (A, i)
 А — матрица i — индекс строки
 Сортировка матрицы по элементам i-й строки
sbval (z, x0, x1, D, load, score)
 z — вектор начальных приближений для недостающих начальных условий

хо — левая граница xl — правая граница

о (х, у) — векторная функция, задающая систему ОДУ

load(xO,z) —векторная функция с начальными условиями

score (xl, у) —векторная функция, задающая правые граничные условия
 Возвращает вектор недостающих начальных условий для двухточечной краевой задачи для системы ОДУ
search (S, Subs, m)
 s — строка Sub — подстрока

m — стартовая позиция поиска
 Стартовая позиция подстроки в строке
•sec(z)
 z — аргумент
 Секанс
sech (z)
 z — аргумент
 Гиперболический секанс
sign(x)
 х — аргумент
 Знак числа
signum(z)
 z — аргумент
 Комплексный знак числа z/ Ы
sin(z)
 z — аргумент
 Синус
sinh (z)
 z — аргумент
 Гиперболический синус
sinfit (x, y,g)
 у — векторы данных

g — вектор начальных значений а,b,с
 Регрессия синусоидой

f (x) =asin (x+b) +с
sine (z)
 z — аргумент
 Sine-функция
SlUnitsOf (x)
 х — аргумент
 Возвращает единицу измерения в системе СИ
slope (x, y)
 х, у — векторы данных
 Коэффициент а линейной регрессии ь+а-х
sort (v)
 v — вектор
 Сортировка элементов вектора
sph2xyz (r, o, ф)
 r, в, ф — сферические координаты
 Преобразование сферических координат в прямоугольные
stack (A, B,C, . . .)
 А, в, с, . . . — векторы или матрицы
 Слияние матриц сверху вниз
Stiffb (y0,t0, t1, M,D, J)
 См. rkf ixed

j ( t , у ) — матричная функция Якоби для D(t,y)
 Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Булирша— Штера
stiffb (y0,t0,t1,

ace, D, J, k, s)
 См. rkadapt

j (t , у) — матричная функция Якоби для D(t,y)
 Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Булирша— Штера (для определения только последней точки интервала)
Stiffr (y0,t0,t1, M, D, J)
 См. Stiffb
 Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Розен-брока
stiffr (y0,t0,t1,acc,

D,J,k,s)
 См. stiffb
 Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Розен-брока (для определения только последней точки интервала)
str2num(S)
 s — строка
 Преобразование строкового представления в действительное число
str2vec(S)
 s — строка
 Преобразование строкового представления в вектор ASCII-кодов
strlen(S)
 s — строка
 Количество знаков в строке
submatrix (A, ir /jr,

ic, jc)
 A — матрица

ir, jr — строки ic, j с — столбцы
 Возвращает часть матрицы, находящуюся между ir , j r-строками и ic, j с-столбцами
substr (S,m,n)
 s — строка
 Подстрока, полученная из строки s выделением n знаков, начиная с позиции m в строке s
supsmooth(x, y)
 x , у — векторы данных
 Сглаживание с помощью адаптивного алгоритма
svd(A)
 А — действительная матрица
 Сингулярное разложение
svds (A)
 А — действительная матрица
 Вектор, состоящий из сингулярных чисел
tan(z)
 z — аргумент
 Тангенс
tanh(z)
 z — аргумент
 Гиперболический тангенс
Tcheb(n,x)
 х — аргумент n — порядок
 Полином Чебышева первого рода
time (x)
 х — аргумент
 Значение системной константы текущего времени
tr(A)
 А — квадратная матрица
 След матрицы
trunc (x)
 х — аргумент
 Целая часть числа
Ucheb (n, x)
 х — аргумент n — порядок
 Полином Чебышева второго рода
vec2str (v)
 v — вектор ASCII-кодов
 Строковое представление элементов вектора v
wave (y)
 у — вектор данных
 Вектор прямого вейвлет-преобразования
WRITE* (file)
 file — строковое представление пути к файлу
 Запись данных в файл типа *
xy2pol (x,y)
 х, у — прямоугольные координаты на плоскости
 Преобразование прямоугольных координат в полярные
xyz2cyl (x,y, z)
 x, y, z — прямоугольные координаты
 Преобразование прямоугольных координат в цилиндрические
xyz2sph (x, y, z)
 x, у, z — прямоугольные координаты
 Преобразование прямоугольных координат в сферические
Y0(x), Yl(x), Yn (m, x)
 x — аргумент, х>0
 Функция Бесселя второго рода нулевого, первого и лт-го порядка
ys (n,x)
 п — порядок х — аргумент
 Сферическая функция Бесселя второго рода

Примечание 1
Примечание 1

Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки — *. Например, различные статистические функции, описывающие различные распределения или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка. Специальных функций комплексного аргумента с измененной нормировкой, а также финансовых функций (см. табл. П3.4) в данном списке нет.

 


П3 1 Арифметические операторы



Таблица П3.1. Арифметические операторы


Оператор
 Клавиша
 Скаляр
 Вектор
 Матрица
="ico1.gif">
 <:>
 Присваивание
="ico2.gif">
 <~>
 Глобальное присваивание&nbsp
="ico3.gif">
 <=>
 Численный вывод&nbsp
="ico4.gif">
 <Ctrl>+<=>
 Символьный вывод&nbsp
="ico5.gif">
 <+>
 Сложение&nbsp
="ico6.gif">
 <->
 Вычитание или отрицание (унарная операция)
&nbsp 		<*>
 Умножение
 Матричное умножение,

Умножение на скаляр
&nbsp &nbsp &nbsp Скалярное произведение
 &nbsp

<Ctrl>+<8>
 &nbsp Векторное произведение
 &nbsp
/либо +
 </> либо <Ctrl>+</>
 Деление&nbsp
="ico9.gif">
 <!>
 Факториал&nbsp
="ico10.gif">
 <">
 Комплексное сопряжение&nbsp
="ico11.gif">
 <\>
 Квадратный корень&nbsp
="ico12.gif">
 <Ctrl>+<\>
 Корень степени m&nbsp
="ico13.gif">
 <'>
 Скобки (изменение приоритета)&nbsp
="ico14.gif">
 Ф
 &nbsp Нижний индекс&nbsp
="ico15.gif">
 <Ctrl>+<1>
 &nbsp Транспонирование
="ico16.gif">
 <Shift>+<\>
 Модуль
 Модуль вектора
 Определитель
="ico17.gif">
 <Ctrl>+<4>
 &nbsp Сумма элементов
 &nbsp
="ico18.gif">
 &nbsp Обратная величина&nbsp
Обратная матрица
="ico19.gif">
 <л>+<п>
 Возведение в степень n
 Возведение матрицы в степень n
="ico20.gif">
 <Ctrl>+<->
 &nbsp Векторизация&nbsp
="ico21.gif">
 <Ctrl>+<6>
 &nbsp Выделение столбца

Примечание 1
Примечание 1

Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.

 


П3 2 Вычислительные операторы



Таблица П3.2. Вычислительные операторы


Оператор
 Клавиша
 Описание
="ico22.gif">
 <Shift>+<7>
 Определенный интеграл
="ico23.gif">
 <Ctrl>+<!>
 Неопределенный интеграл
="ico24.gif">
 <?>
 Дифференцирование
="ico25.gif">
 <Ctrl>+<?>
 Вычисление n-й производной
="ico26.gif">
 <Ctrl>+<Shift >+<4>
 Сумма
="ico27.gif">
 <Ctrl>+<4>
 Сумма ранжированной переменной
="ico28.gif">
 <Ctrl>+<Shift >+<3>
 Произведение
="ico29.gif">
 <Ctrl>+<3>
 Произведение ранжированной переменной
="ico30.gif">
 <Ctrl>+<L>
 Предел
="ico31.gif">
 <Ctrl>+<A>
 Левый предел
="ico32.gif">
 <Ctrl>+<B>
 Правый предел
 




П3 4 Встроенные функции финансового анализа



Таблица П3.4. Встроенные функции финансового анализа


Функция
 Аргументы
 Описание
cnper (rate,pv, fv)
 rate — фиксированный процент по вкладу, rate>-l

pv — текущее значение вклада,

pv>0

f v — будущее значение вклада,

fv>0
 Отвечает числу составных периодов, необходимых для получения будущего значения вклада при заданных текущем значении вклада и проценте начислений
crate (nper,pv, fv)
 nper — целое число составных периодов, nperai

pv — текущее значение вклада,

pv>0

fv — будущее значение вклада,

fv>0
 Отвечает фиксированному проценту начислений по вкладу на период, необходимый для прироста от текущего значения вклада до будущего значения при заданном числе составных периодов
cumint (rate, np er,pv, start, en d, [type])
 rate — фиксированный процент по вкладу, должен быть действительным скаляром, rate>0

nper — общее число составных периодов, должно быть положительным целым числом

pv — текущее значение займа,

pv>0

start — начальный период накопления; должен быть положительным целым числом

end — конечный период накопления, должен быть положительным целым числом, start<end

type=0 для платежа, сделанного в конце периода, или i для платежа, сделанного в начале периода
 Отвечает совокупному проценту по займу между начальным и конечным периодами при фиксированном проценте, общем числе составных периодов и текущем значении займа
cumprn (rate, np er,pv, start, en d, [type])
 См. cumint
 Отвечает совокупной сумме по займу между начальным и конечным периодами при фиксированном проценте, общем числе составных периодов и текущем значении займа
ef f (rate, nper)
 rate — номинальная процентная ставка, должна быть действительным скаляром
 Отвечает эффективной ежегодной процентной ставке при данной номинальной ежегодной процентной ставке и числе составных периодов в год
fv(rate,nper,p mt, [ [pv] , [type ]])
 rate — фиксированная процентная ставка за период, должна быть действительным скаляром,

rate>0

nper — общее число составных периодов в год, nper >0
 Соответствует будущему значению вклада или займа через особое число составных периодов, установленных периодически, при постоянных платежах и фиксированной процентной ставке
cnper (rate,pv, fv)
 rate — фиксированный процент по вкладу, должен быть действительным скаляром,

rate>-l

pv — текущее значение вклада,

pv>0

f v — будущее значение вклада,

fv>0
 Отвечает числу составных периодов, необходимых для получения будущего значения вклада при заданных текущем значении вклада и проценте начислений
crate (nper,pv, fv)
 nper — число составных периодов, должно быть целым числом,

прег>1

pv — текущее значение вклада,

pv>0

f v — будущее значение вклада,

fv>0
 Отвечает фиксированному проценту начислений по вкладу на период, необходимый для прироста от текущего значения вклада до будущего значения при заданном числе составных периодов
cumint (rate, np er,pv, start, en d, [type])
 rate — фиксированный процент по вкладу, должен быть действительным скаляром, rate>0

nper — общее число составных периодов, должно быть положительным целым числом

pv — текущее значение займа,

pv>0

start — начальный период накопления, должен быть положительным целым числом

end — конечный период накопления, должен быть положительным целым числом, start<end

type=0 для платежа, сделанного в конце периода, или 1 для платежа, сделанного в начале периода
 Отвечает совокупному проценту по займу между начальным и конечным периодами при фиксированном проценте, общем числе составных периодов и текущем значении займа
cumprn ( r ate , np er, pv, start, en d, [type])
 См. cumint
 Отвечает совокупной сумме по займу между начальным и конечным периодами при фиксированном проценте, общем числе составных периодов и текущем значении займа
ef f (rate, nper)
 rate — номинальная процентная ставка, должна быть действительным скаляром

nper — общее число составных периодов в год, nper >0
 Отвечает эффективной ежегодной процентной ставке при данной номинальной ежегодной процентной ставке и числе составных периодов в год
fv(rate, nper, p mt, [ [pv] , [type]])
 rate — фиксированная процентная ставка за период; должна быть действительным скаляром,

rate>0

nper — общее число составных периодов в год, nper>0

pv — текущее значение займа

type=0 для платежа, сделанного в конце периода, или 1 для платежа, сделанного в начале периода
 Соответствует будущему значению вклада или займа через особое число составных периодов, установленных периодически, при постоянных платежах и фиксированной процентной ставке
fvadj (prin, v)
 prin — ежегодная общая сумма

v — вектор процентных ставок, каждая из которых применяется с той же самой основной суммой и процентами с нее за период времени
 Соответствует будущему значению ежегодной общей суммы капитала, на который начисляются проценты, при применении серии составных процентных ставок
fvc(rate, v)
 rate — фиксированная процентная ставка за период; должна быть действительным скаляром

v — вектор регулярных денежных потоков
 Соответствует будущему значению серии денежных потоков, происходящих с регулярными интервалами, и приносящими специальную процентную ставку
ipmt (rate, per, nper,pv, [ [fv] , type]])
 rate — фиксированная процентная ставка за период, rate>0

per — период, за который вы хотите найти ставку, должен быть положительным целым числом

nper — общее число составных периодов, per<nper

pv — текущее значение f v — будущее значение

type=0 для платежа, сделанного в конце периода, или 1 для платежа, сделанного в начале периода
 Соответствует процентному платежу по вкладу или займу за данный период, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку и особое текущее значение
irr (v, [guess] )
 v — вектор денежных потоков, определяемых за регулярные интервалы, должен состоять, по крайней мере, из одного положительного и отрицательного числа

guess — численное значение, которым вы предполагаете аппроксимировать ответ; если им пренебрегается, то

guess=0.1 (10%)
 Отвечает внутренней ставке возврата для серии денежных потоков, происходящих с регулярными интервалами
mirr (v, fin rat e,rein rate)
 v — вектор денежных потоков, определяемых за регулярные интервалы, он должен состоять, по крайней мере, из одного положительного и отрицательного числа

fin rate — финансовая ставка платежа по заимствованным денежным потокам

rein rate — ставка реинвестирования
 Соответствует модифицированной процентной ставке возврата для серии денежных потоков с регулярными интервалами при условии, что ставка финансирования подлежит оплате в соответствии с суммой заимствования, а ставка реинвестирования приносит доход с суммы, которую вы повторно инвестируете
nom(rate, nper)
 rate — эффективная ежегодная процентная ставка, должна быть действительным скаляром

rate>-l

nper — общее число составных периодов за год, nper>0
 Соответствует номинальной процентной ставке, включающей эффективную ежегодную процентную ставку и число составных периодов за год
npv (rate, v)
 rate — фиксированная процент^ ная ставка, с которой вклад зарабатывает процент за период, должна быть действительным скаляром

v — вектор регулярных денежных потоков
 Вычисляет чистое текущее значение вклада, включающее скидки и регулярные денежные потоки
nper (rate,pmt, pv, [[fv], [type] ] )
 rate — фиксированная процентная ставка

per — период

nper — общее число составных периодов за год, должно быть положительным целым числом

pmt — платеж, делаемый каждый период

pv — текущее значение вклада f v — будущее значение вклада

type=o для платежа, сделанного в конце периода, или 1 для платежа, сделанного в начале периода

guess — численное значение, которым вы предполагаете аппроксимировать ответ, если им пренебрегается, то

guess=0.01 (10%)
 Отвечает числу периодов для вклада или займа, основанных на периодичности, постоянных платежах, использующих фиксированную процентную ставку, и особое текущее значение
pmt (rate, nper, pv, [ [fv] , [type]])
 См. nper
 Соответствует платежу по вкладу или займу, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку, и особое текущее значение
ppmt (rate, per, nper,pv, [[fv], [type]] )
 См. nper
 Соответствует платежу по общей сумме вклада или займа, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку, и особое будущее значение
pv (rate, nper, pmt, [ [fv] , [type]])
 CM. nper
 Соответствует текущему значению вклада или займа, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку, и особый взнос
rate (nper, pmt, pv, [ [fv] , [type ] , [guess] ] )
 CM. nper
 Соответствует процентной ставке на период вклада или займа при особом числе периодических составных периодов, постоянных платежах и особом текущем значении

 


П4 1 Сообщения об ошибках



Таблица П4.1. Сообщения об ошибках


Ошибка
 Перевод
 Вероятная причина
 Возможные пути устранения

&nbsp Сообщения об ошибках в численных вычислениях A "Find" or "Minerr" must be preceded by a matching "Given"
Find или Minerr должны предваряться ключевым словом Given
Эта ошибка выделяет функцию Find или Minerr при их несогласованности

С Given
Каждый вычислительный блок, который заканчивается функцией Find или Minerr, должен начинаться с ключевого слова Given
All evaluations resulted in either an error or a complex re-suit
Вычисления приводят к ошибке или комплексному результату
Mathcad не может начертить некоторые точки, потому что не существует действительных значений для их нанесения на график
Это сообщение может появиться, если имеется ошибка или все значения комплексные
Arguments in function definitions must be names
Аргументы в определениях функции должны быть именами
Выделенное определение функции содержит неправильный перечень аргументов
В списке аргументов должны быть правильно поименованы переменные или список имен необходимо отделить запятыми
At least one limit must be infinity
По крайней мере один предел должен быть бесконечным
Когда для интегрирования выбран алгоритм бесконечного предела, то по крайней мере один из пределов интеграла должен быть бесконечным
Тип бесконечности вводится нажатием сочетания клавиш <Ctrl>+<Shift>+<Z>.

Для изменения алгоритма, использующего бесконечный предел, или для вычисления какого-либо другого интеграла щелкните на интеграле правой кнопкой мыши и измените алгоритм с помощью контекстного меню
Can only evaluate an nth order derivative when n = 0,1..5.
Можно вычислить n-й порядок производной, только когда

п=0,1. .5
Порядок производной должен быть одним из следующих чисел: 0, 1,2 ..... 5
Если вы хотите посчитать производную более высокого порядка, то делайте это с помощью символьного дифференцирования
Can't evaluate this function when its argument less than or equal to zero
Невозможно вычислить эту функцию, когда ее аргумент меньше или равен нулю
Ошибка может заключаться в использовании неположительных данных на графиках, построенных в логарифмическом масштабе
Отрицательные числа и ноль не могут быть расположены на логарифмических осях. Смените тип осей графика или постройте его для других значений
Can't converge to a solution
Не сходится к решению
Численный метод расходится (не может найти решения)
Убедитесь, что операция не применяется к функции в области непосредственной близости точки ее сингулярности (деления на ноль).

Попробуйте поменять параметры численного метода (например, начальное приближение).

Попробуйте увеличить константу TOL, т. е. осуществить поиск решения с худшей погрешностью.

Попробуйте поменять численный алгоритм, если это возможно (вызвав контекстное меню нажатием на месте ошибки правой кнопки мыши)
Can't define the same variable more than once in the same expression
Невозможно определить ту же самую переменную более одного раза в одном и том же выражении
Вы пытаетесь вычислить одну и ту же переменную дважды в одном выражении
Пример подобной ошибки: если вы создаете вектор с левой стороной а : = и используете это же имя справа, то получите ошибку
Can't determine what units the result of this operation should have
Невозможно определить, в каких единицах следует быть результату этой операции
Вы возвели выражение, содержащее единицы измерения, в степень, являющуюся переменной в неких пределах или вектором. В результате невозможно определить размерность результата
Если выражение включает в себя единицы измерений, то можно возводить его только в действительную фиксированную степень
Can't divide by zero
Деление на ноль невозможно
Где-то в программе или внутри численного метода возникло деление на ноль
Найдите место деления на ноль и устраните его.

Попробуйте поменять параметры численного метода, константы точности или сам численный алгоритм
Could not find a solution
Невозможно найти решение
Численный метод расходится (не может найти решения)
См. "Can't converge to a solution"
Can't find the data file you're trying to use
Невозможно найти файл, который вы пытаетесь использовать
Невозможно найти файл данных или другой тип файла, к которому вы обращаетесь
Удостоверьтесь, что такой файл существует в указанном месте
Can't have anything with units or dimensions here
Здесь нет ничего в единицах измерений или в размерностях
Это выражение использует единицы измерений где-то, где они не разрешены
Единицы измерений не разрешены:

• в аргументах большинства функций;

• в экспонентах;

• в верхних и нижних индексах.

Для того чтобы использовать выражения с единицами измерений, вначале переведите это выражение в UnitsOf
Can't have more than one array in a contour plot
Нельзя иметь более одного массива в контурном графике
Вы вводите более одного массива в местозаполнитель контурного или поверхностного графика
Можно иметь только один массив в данном местозаполнителе, т. к. графики могут выдавать лишь одну поверхность в один момент времени
Can't perform this operation on the entire array at once. Try using "vectorize" to perform it element by element.
Невозможно представить эту операцию в целом массиве сразу. Попытайтесь использовать векторизацию, чтобы представить элемент за элементом
Например, можно увидеть это сообщение при попытке разделить один вектор на другой
Для того чтобы применять функцию или оператор к каждому элементу вектора или матрицы, используйте оператор векторизации
Can't plot this many points
Невозможно начертить график с таким большим количеством точек
Попытка построения графика с числом точек, превосходящим возможное
Попробуйте сделать число точек меньше, чем 150 000
Can't put a ":=" inside a solve block.
Нельзя помещать" :=" внутрь вычислительного блока
Внутри вычислительного блока не должно быть формулировки присваивания. Он должен содержать только булевы выражения
Используйте панель с булевыми операторами
Can't raise an expression having units to a complex power
Нельзя возводить в комплексную степень выражение, имеющее единицы измерений
Это выражение содержит единицы измерений, а вы возводите его в комплексную степень
Выражение с единицами измерений можно возводить только в действительную степень. Для того чтобы возводить в комплексную степень выражение с единицами измерений, вначале переведите это выражение в SlUnitsOf — единицы измерений будут отменены
Can't solve a system having this many equations
Невозможно решить систему, имеющую так много уравнений
Mathcad не способен решить систему
См. определение термина "вычислительный блок " (разд. 5. 1)
Can't understand something in this data file
Невозможно что-то понять в файле данных
Файл, к которому вы пытаетесь получить доступ при помощи

READ ИЛИ READ*,

имеет дефект
Файл должен быть ASCII-текстом.

Все строки файла должны иметь тот же номер значений, что используется в READ*.

Если файл имеет требуемый формат, а это сообщение продолжает появляться, попробуйте удалить любую часть текста из файла
Can't understand the name of this function
Невозможно понять имя этой функции
Такое сообщение может появиться, если в качестве имени функции используется, например, число 6 (х)
Выражение должно соответствовать требованиям, предъявляемым в Mathcad к написанию имен функций
Can't understand the way this range variable is defined
Невозможно понять определение ранжированной переменной
Определение ранжированной переменной неверно
Вводя область определения ранжированной переменной, необходимо использовать один из следующих видов:

• Rvar : = nl . . n2

• Rvar := nl,n2 . .пЗ
Can't understand this number
Невозможно понять это число
Это выражение содержит символ или десятичную точку там, где это непозволительно
Вы увидите эту ошибку, например, если случайно запишете число так: ".452."
Can't use a range variable in a solve block.
Невозможно использовать ранжированную переменную в вычислительном блоке
Эта ошибка появится, если использовать область определения переменной в неподходящем месте
Придумайте алгоритм, не допускающий применение ранжированной переменной в вычислительном блоке
Cannot evaluate this accurately at one or more of the values you specified
Невозможно точно вычислить одно или более значений
Эта ошибка появляется, если попытаться вычислить функцию для аргумента, находящегося за пределами точной области определения функции
Проверьте область определения функции
Cross product is defined only for vectors having exactly three elements
Векторное произведение определяется только для векторов, имеющих точно три элемента
Возможно, предпринята попытка вычислить векторное произведение для векторов, имеющих не три, а другое количество элементов
См. определение векторного произведения (разд. 7.2.3)
Can't evaluate this expression. It may have resulted in an overflow or an infinite loop
Невозможно вычислить это выражение. Это может быть результатом переполнения или бесконечных циклов
Это функциональное определение может содержать слишком много вложенных функций. Или функция может быть константой в бесконечных циклах
Проверьте несколько итераций цикла
Degree of the polynomial must be between 1 and 99.
Степень полинома должна находиться в пределах между 1 и 99
Вектор, пропущенный через функцию поиска корней полинома, должен содержать, по крайней мере, 2 и не более 99 элементов
Dimensions must be > 4
Размерность должна быть > 4
Эта матрица должна иметь, по крайней мере, 4 ряда и 4 столбца
&nbsp End of file
Конец файла
Вы пытаетесь прочитать больше значений в файле данных, чем там имеется
Например, если файл данных имеет 10 значений, а записано выражение i : =1 . . .100

xi:=READ* (file) , то появится это сообщение
End points cannot be the same
Конечные точки не могут быть одинаковыми
Это сообщение появляется при некорректном решении дифференциальных уравнений
Конечные точки интервала, на котором будет вычисляться решение, должны быть различны
Equation too large
Уравнение слишком большое
Это выражение слишком сложное для вычисления
Разбейте выражение на несколько простых
Floating point error
Ошибка вычислений с плавающей точкой
Функция вычисляется в точке, в которой это запрещено
&nbsp Found a singularity while evaluating this expression. You may be dividing by zero
Найдена сингулярность при вычислении этого выражения. Возможно, вы делите на ноль
Вычисляется функция или выполняется операция с недопустимым значением
Например, это сообщение возникнет при попытке деления на ноль или обращения сингулярной матрицы; разберитесь, где это происходит
Found a number with a magnitude greater than 1ГГ307
Найдено число, превышающее значение 10307
&nbsp Попробуйте поменять параметры численного алгоритма или сам алгоритм
Illegal context. Press <F1 > for help
Недопустимый контекст. Нажмите <F1>, чтобы получить помощь
Часто встречается при синтаксических ошибках
Проверьте синтаксис и порядок расположения формул в документе
Illegal dimensions
Недопустимые размерности
Матрица, на которую вы ссылаетесь, не имеет достаточно строк или столбцов
Введите имя матрицы с клавиатуры и нажмите знак "=", чтобы проверить число ее строк и столбцов
Integer too large/ Integer too small
Целое число слишком большое/слишком маленькое
Это число слишком велико/мало для работы с ним
Если вы работаете со встроенными функциями, то щелкните левой кнопкой мыши на имени функции и вызовите подсказку с помощью клавиши <F1>
Invalid format
Недопустимый формат
Аргументы этой функции могут быть некорректны
Если вы работаете со встроенными функциями, то щелкните левой кнопкой мыши на имени функции и вызовите подсказку с помощью клавиши <Р1>
Live symbolics not available
Символьные вычисления неприменимы
&nbsp &nbsp Must be <= <=10000
Значение должно быть <=10000
&nbsp &nbsp Must be >= >=1CT-16
Значение должно быть >=1 0"16
&nbsp &nbsp Must be string
Функция или оператор должен быть строковым аргументом
&nbsp См. разд. 1.2.5
Must be function
Аргумент должен быть функцией
&nbsp &nbsp Must be increasing
Значения вектора должны быть возрастающими
&nbsp Введите с клавиатуры имя вектора и знак "=", чтобы проверить его значения
Must be less than the number of data points
Должен быть меньше, чем число точек данных
Этот аргумент должен быть меньше, чем число точек имеющихся данных
Must be positive
Должен быть положительным
Невозможно вычислить функцию, когда ее значения меньше или равны нулю
Это сообщение может касаться построения X-Y или полярных графиков с логарифмическими осями. Отрицательные числа или ноль не могут располагаться на логарифмических осях
Must be real
Должно быть действительным
Это значение должно быть действительным. Его мнимая часть должна быть нулем
Примером таких выражений могут служить нижний и верхний индексы, решения дифференциальных уравнений, углы
Must be real scalar
Должен быть действительным скаляром
Это значение не должно быть комплексным или мнимым
&nbsp Must be real vector
Должно быть действительным вектором
Этот вектор не может иметь комплексные или мнимые элементы. Он должен также быть вектором -стол бцом , а не строкой
&nbsp Must be square
Должна быть квадратной
Эта ошибка выделяет неквадратную матрицу в той операции или функции, в которой ей следует быть квадратной
Например, матрица должна быть квадратной при обращении, возведении ее в степень, или в функциях eigenvals и eigenvec
No solution found
Не найдено решение
&nbsp Если вы используете встроенные функции, то щелкните левой кнопкой мыши на имени функции и нажмите клавишу <F1> для того, чтобы быть уверенным в корректности использования функции. Однако решение может просто не существовать.

См. также "Can't converge to a solution"
Not enough memory for this operation
Для этой операции недостаточно памяти
Не хватает памяти, чтобы завершить это вычисление
Попытайтесь освободить немного памяти путем уменьшения массива или матрицы (Matticad тратит около 8 байт памяти на каждый элемент матрицы) или удаления каких-либо больших побитовых отображений, массивов, матриц
Singular matrix
Сингулярная матрица
Эта матрица не может быть ни сингулярной, ни близкой к сингулярности
Матрица называется сингулярной, если ее определитель равен нулю. Матрица близка к сингулярной, если она имеет высокое число обусловленности (см. главу 9)
The expression to the left of the equal sign cannot be defined
Выражение слева от знака равенства не может быть определено
В левой части находится что-то, что не является допустимым определяемым выражением
В левой части можно разместить одно из следующих определений:

• имя переменной;

• имя переменной с верхним или нижним индексом;

• явный вектор или матрицу;

• имя функции с аргументами f (х,у).

Любые другие выражение недопустимы
The number of rows and/or columns in these arrays do not match
Число рядов и/или столбцов в этих массивах не согласовано
Попытка произвести матричные или векторные операции над массивами, размеры которых не совпадают
Например, сложение двух матриц разного размера недопустимо. Матричное умножение требует, чтобы число столбцов первой матрицы совпадало с числом строк второй (см. разд. 9. 1)
The units in this expression do not match
Размерности в этом выражении не согласованы
Это сообщение появится, если складываются два элемента разной размерности, либо создана матрица, элементы которой имеют разную размерность, либо вы пытаетесь решить систему уравнений для неизвестных переменных разной размерности
Проверьте использование размерных переменных
There is an extra comma in this expression
В выражении лишняя запятая
&nbsp Запятые должны использоваться для того, чтобы отделять:

• аргументы в функции;

• первые два элемента области в определении интервала;

• выражения в графике;

• элементы во входной таблице;

• нижние индексы в матрице.

Любые другие применения запятой приводят к ошибке. Например, запись 4,000 неправильная, а запись 4 000 — правильная
This expression is incomplete. You must fill in the placeholders
Выражение неполное. Необходимо добавить содержимое в местозаполни-тели
Не заполнены указанные местозапол-нители
Необходимо дописать числа или выражения в указанные местоза-полнители
This expression is incomplete. You must provide an operator
Выражение неполное. Необходимо вставить оператор
Не заполнены ме-стозаполнители оператора или пустое пространство между двумя операндами
Это могло произойти при удалении оператора; проверьте правильность ввода выражения
This function has too many arguments
Функция имеет слишком много аргументов
Выделенное выражение содержит функцию с числом аргументов большим, нежели требуется
Проверьте правильность применения функции
This function is undefined at one or more of the points you specified
Функция не определена для одной или более точек
Попытка вычисления оператора или функции с неподходящими значениями
Например, вычисление -3! и ln ( 0 ) — приведет к ошибке, т. к. факториал не определен для отрицательного числа, а логарифм для нуля
This function needs more arguments
Функции не хватает аргументов
Выделенное выражение содержит функцию с меньшим, нежели требуется, числом аргументов
Для встроенных функций щелкните левой кнопкой мыши на имени функции и воспользуйтесь подсказкой <F1>, чтобы проверить правильность числа и типа аргументов. Для функции пользователя проверьте ее определение
This operation can only be performed on a function
Операция может применяться только для функций
Этот аргумент должен быть функцией
Для встроенных функций щелкните левой кнопкой мыши на имени функции и воспользуйтесь подсказкой <F1 >
This operation can only be performed on an array. It can't be performed on a number
Операция может применяться только для массивов. Она не может быть использована для чисел
&nbsp Например, это сообщение появится, если переменная верхнего индекса определена как скаляр. Поскольку переменная верхнего индекса представляет собой столбец матрицы, то ее следует определять как вектор.

Для поверхностных или контурных графиков массив данных должен иметь, по крайней-мере, два ряда и два столбца
This operation can only be performed on a number or an array
Операция может применяться только для чисел или массивов
Используемая функция или оператор требуют представления в виде константы, матрицы или вектора
&nbsp This operation can only be performed on a string
Эта операция может применяться только для строк
Используемая функция или оператор требуют представления в виде строки. Например, строковые функции обычно требуют, по крайней мере, одного строкового аргумента
&nbsp This subscript is too large
Нижний индекс слишком велик
Попытка использовать верхний или нижний индекс, который превышает ограничения
&nbsp This value must be a matrix
Значение должно быть матрицей
Попытка произвести матричную операцию не над матрицей
&nbsp This value must be a vector. It can be neither a matrix nor a scalar
Значение должно быть вектором. Оно не может быть ни матрицей, ни скаляром
Это сообщение маркирует матрицу или скаляр в операциях, которые требуют вектора (одностолбцового массива). Например, суммирование элементов вектора
&nbsp This value must be an integer greater than 1
Значение должно быть целым числом, превосходящим единицу
Значение должно быть > 1
При использовании встроенных функций щелкните левой кнопкой мыши на имени функции и нажмите клавишу <F1 >
This variable or function is not defined above
Переменная или функция не определена выше
Имя неопределенной функции будет помечено красным цветом
Удостоверьтесь, что эта функция или переменная определена выше. Это сообщение появится, если переменная некорректно используется в глобальном определении. Эта ошибка часто свидетельствует о том, что другое уравнение выше в документе является ошибкой. В этом случае все выражения, использующие выражение с ошибкой, будут помечены красным цветом
Underflow
Потеря значимости (исчезновение значащих разрядов)
Из-за ограничений, присущих представлению чисел на компьютере, числа, которые слишком малы, не могут быть представлены. Это сообщение появляется, когда выражение включает такое число. Иногда, особенно в сложных вычислениях, промежуточный результат будет слишком мал, и вся разрядная сетка заполнится нулями
&nbsp Value of subscript or superscript is too big (or too small) for this array
Значение нижнего или верхнего индекса слишком велико (или слишком мало) для этого массива
Это выражение использует нижний или верхний индекс, который относится к несуществующему элементу массива
&nbsp This is not a scalar. Press <F1 > for help
Это не скаляр. Нажмите клавишу <F1 >, чтобы получить помощь
Использован вектор или выражение с интервалами, или какой-то другой тип выражения, где требуется применение скаляра
&nbsp You have one solve block inside another. Every "Given" must have a matching "Find" or "Minerr"
Один вычислительный блок содержится внутри другого. Каждому ключевому слову Given должно сопоставляться Find или Minerr
Указаны два ключевых слова Given подряд без Find или Minerr посередине. Вычислительный блок не может иметь внутри себя другой вычислительный блок
В качестве альтернативы можно задать функцию в терминах одного вычислительного блока и использовать ее внутри другого вычислительного блока. Во многих случаях это дает тот же самый эффект
You interrupted calculation. To resume, click here and choose "Calculate" from the "Math" menu
Вычисления прерваны. Для того чтобы продолжить, щелкните здесь и выберите пункт Calculate меню Math
&nbsp Вычисления прерваны нажатием клавиши <Esc>. Для того чтобы пересчитать выделенное уравнение, наведите на него курсор и воспользуйтесь меню Math / Calculate (Математика / Вычислить)

&nbsp Сообщения об ошибках в символьных вычислениях Argument too large (Integer too large in context, Object too large)
Аргумент слишком велик
Обычно это результат вычисления выражения с плавающей точкой со значением большим, чем около 10x10 миллиардов
&nbsp Discarding large result
Сброс большого результата
Ответ слишком велик для отображения его в отформатированной математической области
Можно разместить ответ в буфе-эе обмена
Expecting array or list
Ожидается массив или список
Операторы в упрощаемом или вычисляемом выражении требуют векторных или матричных операндов
&nbsp Expression contains nonsymbolic operators
Выражение содержит несимвольные операторы
Применена символьная операция к выражению, содержащему местоза-полнители оператора или переменной
&nbsp Floats not handled
С плавающей запятой не поддерживается
Команда Factor была применена к выражению с десятичным числом
&nbsp Illegal function syntax
Недопустимый синтаксис функции
Символьный процессор не может интерпретировать выражение, подобное (f) (X)
&nbsp Invalid arguments
Недопустимые аргументы
Символьный процессор не может выполнить требуемую операцию для данных аргументов
Это сообщение появится, если, например, применить скалярную функцию к массиву без использования оператора векторизации и выбрать команду Symbolics / Simplify (Символика / Упростить)
Invalid range
Недопустимый интервал
Для поиска численного решения уравнения символьный процессор пытается вычислить одну из своих встроенных функций за пределами области ее определения
&nbsp No answer found; stack limit reached
Ответа не найдено
Символьный процессор достиг предела своих возможностей без вычисления или упрощения, которое затребовал пользователь
&nbsp No answer found
Ответа не найдено
Символьный процессор не смог найти точного решения уравнения
&nbsp No closed form found for
Не найдено замкнутой формы для
Символьный процессор не смог найти интеграл, или сумму, или произведение в замкнутой форме
&nbsp Syntax error
Синтаксическая ошибка
Обычно результат применения символьной операции в неподходящих или некорректных выражениях. Символьные вычисления выражений с размерностями также приведут к появлению этого сообщения
&nbsp

 
Содержание




Ресурсы Mathcad



Ресурсы Mathcad



Ресурсы Mathcad (Mathcad Resource) — это библиотека электронных книг, поставляемая вместе с Mathcad 12. Она содержит обширную справочную информацию и обладает всеми свойствами электронных книг, подключаемых к Mathcad. Ресурсы представляют собой сборник примеров решения различных математических, физических и инженерных задач и содержат справочную информацию о возможностях Mathcad. Ресурсы содержат очень большое количество информации, пополняемое от одной версии Mathcad к другой. Практически по любому разделу математики и любому методу решения той или иной задачи в Mathcad здесь можно найти справочные сведения. Приведем краткий перечень глав электронных книг Ресурсов.

 


П5 1 Tutorials (Учебники)



Таблица П5.1. Tutorials (Учебники)


Название учебника Описание

Overview and Quick Tour

(Обзор Mathcad и Быстрый старт)
 Учебник для тех, кто делает первые шаги в Mathcad и абсолютно с ним не знаком, но хочет быстро начать собственные расчеты. Содержит вводные замечания о том, что можно делать при помощи Mathcad, и рассказ о его основных возможностях
New Features in Mathcad 12

(Новые возможности)
 Учебник, адресованный давним пользователям Mathcad, уже имевшим дело с его прежними версиями и которым будет интересно познакомиться с реальными примерами использования новых возможностей версии 1 2
Getting Started Primers

(Учебник для начинающих)
 Очень полезный для новых пользователей интерактивный учебник, который шаг за шагом продемонстрирует пользователю все возможности Mathcad, без знания которых трудно проводить какие бы то ни было расчеты
Features in Depth

(Возможности)
 Учебник для пользователей, имеющих опыт работы с интерфейсом, нацеленный на раскрытие основных возможностей Mathcad и приемов решения конкретных задач
Where to Get More Help (Как получить дополнительную справку)
 Информация о способах получения дополнительной справки
 




П5 2 OuickSheets (Быстрые шпаргалки)



Таблица П5.2. OuickSheets (Быстрые шпаргалки)


Название шпаргалки About QuickSheets (О шпаргалках) Описание
Справочная информация по использованию Шпаргалок
Vectors and Matrices (Векторы и матрицы)
 См. главы 7, 8
Solving Equations (Решение уравнений)
 См. главы 5, 6
Graphing and Visualization (Построение графиков и визуализация данных)
 См. разд. 1.4
Calculus and Differential Equations

(Вычисления и дифференциальные уравнения)
 См. главы 9- 11
Engineering applications (Инженерные приложения)
 Примеры применения Mathcad для решения инженерных и научных задач
Mathcad Techniques (Технические приемы)
 См. главы 1, 2
Data Analysis (Анализ данных)
 См. главы 13—14
Statistics (Статистика)
 См. главу 12
Using Mathcad with Other Applications

(Mathcad и другие приложения)
 примеры подключения к расчетам Mathcad других приложений
Symbolic Math (Символьная математика)
 См. главы 1, 2
Programming (Программирование)
 См. разд. 1.3.5
Extra Math Symbols (Дополнительные математические символы)
 Сводка математических символов
Reference Tables (Таблицы)
 Электронная книга с самой разной справочной информацией из области математики, физики, химии
User's guide (Руководство пользователя)
 Справочное руководство

 


Улучшенный редактор, повышенная эффективность команд



Новые возможности Mathcad 11


 Расширенные возможности импорта и экспорта данных в текстовом формате и формате Microsoft® Excel, введены функции ввода/вывода в двоичные файлы (READBIN и WRITEBIN).   Улучшенный редактор, повышенная эффективность команд Undo и Redo, немного модернизированный математический процессор, улучшенный RTF-экспорт и возможность обычного открытия файлов с удаленных серверов по протоколу HTTP.  Расширенный класс поддающихся решению дифференциальных уравнений в частных производных (введена дополнительная встроенная функция для решения параболических и гиперболических уравнений).  Расчет ряда специальных функций с комплексными аргументами, таких как функции округления, интегралы ошибок, а также функции Бесселя и Ганкеля.  Новая функция sine с улучшенным вычислением значений sin(x) /x при х, стремящемся к 0.  Доступ к начальным значениям, использующимся в генераторах последовательностей псевдослучайных чисел.  Изменения некоторых меню, панелей и диалогов, в частности, вместо меню Math (Математика) введено меню Tools (Сервис).  Руководство пользователя в формате PDF.
 



Новый более быстрый математический процессор



Новые возможности Mathcad 12


  Новый более быстрый математический процессор (см. разд. 1.2. 1).  Модернизированный аппарат работы с размерными перемеменными, статическая проверка размерности, новые единицы измерения (ангстрем и т. д.) (см. разд. 1.2.7).  Новый формат файлов на основе XML-разметки (см. разд. 1.1.1)  Новые опции комментирования документов (примечания и метаданные) (си. разд. 1.3.4).  Новые удобные опции импорта данных из внешних файлов (см. разд. 13.3.3).  Возможность построения второй оси у на двумерных графиках (см. разд. 1.4.6).  Новые встроенные функции генерации массивов для повышения удобства построения графиков в логарифмическом масштабе (см. разд. 1.4.6).  Новый тип данных NaN (НеЧисло) (см. разд. 1.2.5).  Новые функции корреляционного анализа сигналов (см. разд. 12.2.5).  Контроль правильности ввода оператора определителя матрицы и длины вектора (см. разд. 7.3. 1).  Улучшенная работа функций округления (см. разд. 2.2.2).  Восстановление функции until (см. разд. 2.2.2).  Упразднение функции (символа) § (см. разд. 2.2.2).  Новая функция time для хронометрирования вычислений (см. разд. 2.2.3).  Новые масштабированные функции Эйри (см. разд. 2.2.4).  Усовершенствование алгоритма регрессии общего вида (см. разд. 13.2.4).  Ограничение на форму записи неизвестных в пределах вычислительного блока (см. разд. 5.1. 1).  Запрещение рекуррентного задания функций (см. разд. 1.2.4).  Возможность переопределения встроенных и пользовательских функций и переменных при помощи нового именного оператора (см. разд. 1.2.4).  Изменения в работе строковых функций str2num и vec2str (см. разд. 1.2.5).  Константа ORIGIN теперь может относиться и к строковым переменным (см. разд. 1.2.5).

 


Новые возможности Mathcad 2001 и 2001i



Новые возможности Mathcad 2001 и 2001i


 Улучшенный процессор, позволяющий проводить высокоскоростные расчеты, т. н. режим ускоренных вычислений (higher speed calculation). Оптимизация вычислений, улучшенное вычисление неопределенных выражений типа 0ln(0) и предварительная проверка матриц на сингулярность.  Повыщенные возможности организации гиперссылок, в том числе из одного региона на другой, что осуществляется расстановкой тегов.  Новые встроенные функции и возможности:

 функции преобразования декартовых, сферических, цилиндрических координат;  новые функции регрессии, например, логарифмической и линейной специального вида;  семейство lookup-функций для выборки значений из матриц;  функции оцифровки звука из звуковых файлов;  новый тип графика для подготовки классических гистограмм;  возможность представления числа в виде простой дроби.

 Улучшенная связь с другими приложениями благодаря вставке компонентов.  Новые мощные средства для вставки и редактирования рисунков, в том числе панель Picture (Рисунок).  В Mathcad 20011 введена новая встроенная функция для решения жестких систем обыкновенных дифференциальных уравнений Radau, не требующая явного ввода в качестве аргумента якобиана системы.